鱼骨型仓库布局下拣货方式的选择

刘旺盛,江雨瑶,马国旺,曾 艳

(集美大学航海学院,福建 厦门 361021)

0 引言

目前,绝大多数的企业仓库依然使用的是竖直通道这种传统布局,然而Gue 等[1]提出了两种新的仓库布局:flying-V(V 型)布局和fishbone(鱼骨型)布局(见图1),并且证明了在总货位量相等的情况下,V 型仓库从对角线交叉通道垂直延伸的设计可以减少8%～12%的工人预期旅行距离;鱼骨型仓库从对角线交叉通道水平和垂直延伸的设计可以将预期的移动成本降低20%以上。大量的研究人员对这两种新型仓库布局进行了深入研究:Pohl 等[2]、Cardona 等[3]对鱼骨型仓库提出了最佳仓库布局方法;Rakesh 等[4]、Zhou 等[5]、张新艳等[6]和刘建胜等[7]都基于鱼骨型仓库布局,对仓库拣货路径进行了优化。在上述研究基础上,本文采用移动成本最低的鱼骨型仓库布局来讨论基于订单数据的拣货方式的选择。

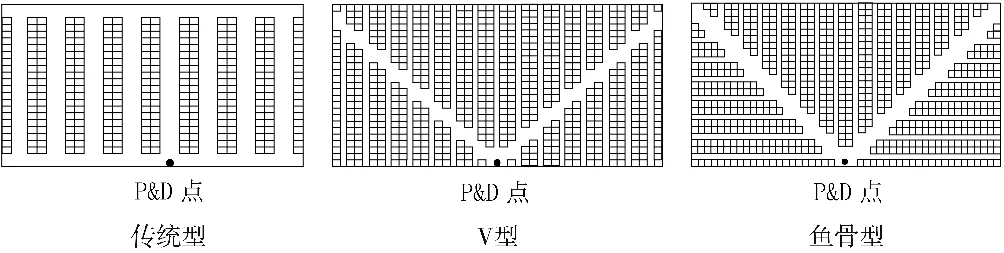
图1 传统型仓库、V 型仓库以及鱼骨型仓库布局

订单拣选是仓库和库存管理活动的重要组成部分,订单拣选成本占仓库成本的一半[8]。拣货作业在仓库的总作业中显得尤为重要,并且越靠近供应链下游客户的订单越呈现出“多品种、多频次、少量”的特点[9],因此对于配送中心而言,选择一种合适的拣货方式非常重要。基本的拣货方式有两种:单一订单拣选和批量拣选[10],也即“摘果式”拣货和“播种式”拣货。

“摘果式”拣货方式是指拣货员按照订单的要求前往仓库拣货区,逐一将订单上货品拣出的过程。“播种式”拣货方式是指在进行拣取工作之前,将一定时间内的所有订单集合成一个拣货批次,再将货品按照品项进行分类汇总,然后将这些商品从拣货区拣出,放到二次分拣区,之后再由员工根据每张客户订单进行二次分拣的过程。

由于科技的发展,用于提高仓库拣货作业效率的技术也越来越多,有学者针对“摘果式”和“播种式”两种拣货方式设计了电子标签分拣技术[11]和光线指引辅助拣选技术[12],用来加快拣货速度、减少出错率。因为两种拣货方式的作业工序不同,每种拣货方式有其适用的场景,更多的研究是在单一的拣货方式基础上进行,例如Donald 等[13]在“摘果式”拣货的基础上讨论了如何设计仓库来减少拣货移动距离,Grosse 等[14]在“播种式”拣货基础上讨论人的因素对订单拣选的影响,Islar 等[15]对“摘果式”拣选路径进行优化,田维彬[16]在“播种式”拣货基础上对仓库储位进行优化,黎妙娟[17]通过排队理论解决了“播种式”拣选订单的资源配置问题。很多研究是采用定性的方法对“摘果式”和“播种式”两种拣货方式的优缺点以及适用条件进行了细致的描述[18-19]。柯晟劼[20]以作业时间为评价标准,基于订单数据四个要素建立了拣货方式作业时间模型,以此用定量的方法来为物流配送中心选择恰当的拣货方式。蒋发[21]基于订单数据中的四个要素,以订单品项的重合度为核心,设立动态标准线,用定量的方法得到对应的拣货方式。

综上,很少有研究涉及拣货方式的选择,少数对拣货方式选择的研究基本是基于经验和定性分析,进行定量化比较的较少,并都是基于传统型仓库布局下的讨论,未见有基于鱼骨型仓库布局下拣货方式选择的研究。但鱼骨型仓库库内行走成本更低,因此本文基于鱼骨型仓库,建立两种拣货模式下的拣货作业时间模型,通过比较这两种拣货作业时间,探讨分析各种情形下理想的拣货方式。

1 基本概念和流程

1.1 鱼骨型仓库模型

本文选取的鱼骨型仓库的入库以及出库操作不在同一时间,仓库布局如图2所示。鱼骨型仓库只有一个仓库门,每次存取货后都必须回到该仓库门等待下一次的存取操作,因此该仓库门就是仓库的起始点,即P&D 点。该仓库采取的是人到货拣选系统,拣货员从不同的存储位置上收集订单上的货品[22]。该鱼骨型仓库布局分为四个拣货区,货区编号如图依次为①、②、③、④,仓库布局左右对称。布局中有两条斜主通道、前后左右四条主通道、两货架之间的拣货通道、货位以及P&D 点左右两边的分拣台。仓库内货位按照品项种类存放商品。设r(r=1,2,3,4)表示货区号,x(x=1,2,3,…,xmax)表示货架的排数,y(y=1,2,3,…,ymax)表示货架的列数。图2标明了各区货架排和列的编号顺序,每一个货位都有固定的编号,(r,x,y)表示位于r区x排y列的货位,如P&D 点编号为(0,0,0),(2,5,3)表示2 区5 排3列。拣货通道号与货架的排数之间存在规律,可用货架排数表示拣货通道号。对该鱼骨型仓库布局作以下假设:

图2 鱼骨型仓库基本结构

(1)每个货位的几何尺寸一样,不考虑货架的高度;

(2)拣选距离不考虑同一个通道左右两侧货物拣选时行走的距离;

(3)拣货通道的两端都可以进入,允许在通道内折回;

(4)该仓库存在一个P&D 点,拣货人员从该P&D 点出发,结束拣货后回到该P&D 点;

(5)一次订单拣选总量不超过拣货车的最大载重量。

1.2 订单数据概念界定

订单数据的四个要素分别为:客户数E(order entry)、商品种类数I(item)、订货数量Q(quantity)、订单列表行数L(order list line)。田维彬[16]对这四个要素进行交叉分析得到:每张客户订单的订货品项数量用EN表示,每张客户订单的总订货数量用EQ表示,各商品种类的总订货数量用IQ表示,每个商品种类的订货次数用IK表示。

1.3 “摘果式”拣货方式的作业工序

根据黄晨璐[10]的研究,“摘果式”拣货方式以客户订单为拣选单,一次拣选完成一个客户订单,不需要再进行分货。具体作业工序如下:

①准备工作:生成拣选资料,拣货员领取拣货单(即客户订单),准备周转箱以及推车等;

②对照拣货单:拣货员对照拣货单查看待拣商品;

③移动:拣货员步行至货品存放的货架位置;

④拣取放入:拣货员将确认无误的商品拣取放入周转箱;

⑤结束返回:反复进行工序②→④直至拣货单(即客户订单)上面的商品全部拣出,返回出发点。

⑥反复进行②→⑤工序直至全部客户订单都拣货完成。

具体作业流程如图3所示。

图3 “摘果式”拣货方式的作业流程

分析发现“摘果式”拣货作业工序中较花费时间的有3 道工序:对照拣货单、移动、拣取放入。其中“移动”这道工序花费时间最多,“对照拣货单”以及“拣取放入”花费时间较少。

1.4 “播种式”拣货方式的作业工序

根据黎妙娟[17]的研究,“播种式”拣货作业分为两个阶段:第一阶段,先将客户订单汇合,之后按照商品品类集合形成集合单进行拣选;第二阶段,按照客户订单进行二次分拣。具体作业工序如下。

(1)第一阶段:

①准备工作:对客户订单集合并形成集合单,拣货员领取集合单,准备集货箱以及推车等。②对照集合单:拣货员对照集合单查看待拣商品。③移动:拣货员步行至货品存放的货架位置。④拣取放入:拣货员将确认无误的商品拣取放入集货箱。⑤结束返回:集合单商品拣选完毕,返回分拣台。反复进行工序②→⑤直至所有客户订购的商品全部拣出,然后进入第二阶段。

(2)第二阶段:

①准备工作:领取拣货单(即客户订单),准备周转箱以及推车等。②移动:拣货员步行至集货箱放置处(即分拣台)。③对照拣货单:拣货员对照拣货单查看集货箱。④拣取放入:拣货员将集货箱中确认无误的商品拣取放入周转箱,反复进行工序②→④直至拣货单上面的商品全部拣出(因为在分拣台各集货箱相邻放置,所以在分拣同一个拣货单的时候只重复进行②与④,因③移动距离太短忽略不计)。⑤结束返回:拣选单商品拣选完毕,返回出发点。按照客户订单进行分货,直至把第一阶段集合的全部商品分完。“播种式”拣货作业流程如图4所示。

图4 “播种式”拣货方式的作业流程

分析发现“播种式”拣货作业工序中较花费时间的有6 道工序,分别是两个阶段中的情况:(1)对照单据;(2)移动;(3)拣取放入。其中“移动”这道工序花费时间最少,“对照单据”以及“拣取放入”花费时间较多。

2 拣货方式作业时间的建模

2.1 问题描述

根据国内外研究,对于如何选择理想的拣货方式缺乏合理的定量化标准,文献[20]基于订单数据提出了以拣货作业时间为拣货方式选择的标准,但其对拣货流程中移动工序所涉及的研究不深,对“播种式”第二阶段的作业时间计算不完善,整体实际应用性不强。针对这一问题,本文在文献[20]的基础上,基于旅行成本最低的鱼骨型仓库来对移动工序所花费的时间进行计算,并且完善了“播种式”拣选第二阶段的作业时间,基于订单数据中的四个要素建立了拣货作业时间模型,以拣货作业时间为标准来定量化选择理想的拣货方式。

2.2 鱼骨型仓库拣货移动距离求解模型

基于旅行成本最低的鱼骨型仓库分析拣货作业中的移动距离。

参数设置:

G:货物的重量;

Gmax:拣货车的最大载重量;

n:一次拣选作业中待拣选点的数目;

i、j:待拣选点集合中任意的拣选点;

z:分拣台所在位置;

dij:任意拣选点i、j间的距离;

d01:第一个拣货点到P&D 点的距离;

dn0:最后一个拣货点到P&D 点的距离;

Ai:拣选点i所在的通道号;

Ki:拣货点i所在的货区号;

Si:拣选点i到通道起始端的距离;

Li:拣选点i所在的通道的长度;

a:相邻拣货通道间的距离;

b:相邻拣货通道斜主干道的长度;

v:拣货通道转至前后主通道或左右主通道行走的距离;

w:拣货通道转至斜主通道行走的距离;

X:分拣台到左右主通道起始端的距离;

Y:分拣台到P&D 点的距离;

Uij:拣选完i后是否前往拣选点j

式(1)表示如果拣选完i点后立即去拣选点j拣选则取值为1,否则取值为0;式(2)和式(3)表示每个待拣选点只能被拣选一次;式(4)表示拣货作业从P&D 点开始,拣货作业完成后需要回到P&D 点;式(5)表示一次订单拣选总量不超过拣货车的最大载重量。

根据仓库布局的对称性,两拣货点在②④区和③④区的距离公式分别参照①③区和①②区。根据上述参数设计,鱼骨型仓库布局简图如图5所示。

图5 鱼骨型仓库布局简图

下面对两拣货点间距离dij进行分类计算:

(1)P&D 点与任意的拣选点的距离;

(2)任意两个拣选点之间的距离:

a)位于同区的两拣货点距离;

b)分别位于①②区的两拣货点距离;

c)分别位于①③区的两拣货点距离;

d)分别位于①④区的两拣货点距离;

e)分别位于②③区的两拣货点距离。

以上的两种分类涵盖了鱼骨型仓库布局中所有的两点间的拣货距离。

P&D 点与任意的拣选点的距离公式:

(1)位于同区的两拣货点距离公式:

(2)分别位于①②区的两拣货点距离公式:

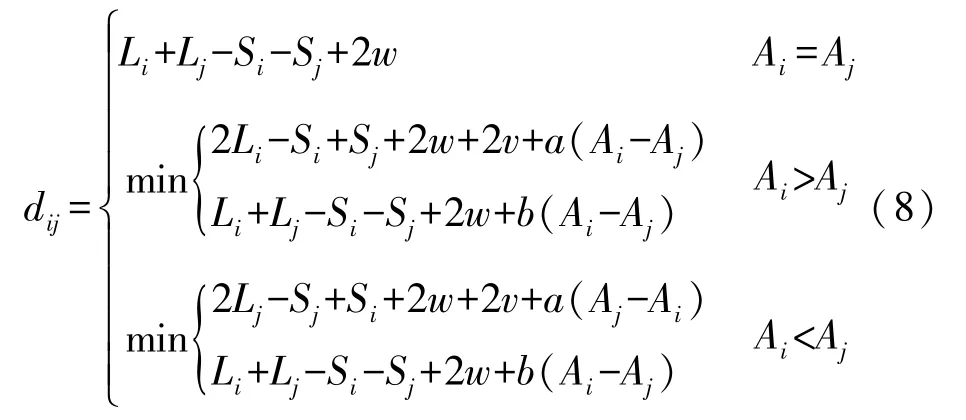
(3)分别位于①③区的两拣货点距离公式:

(4)分别位于①④区的两拣货点距离公式:

(5)分别位于②③区的两拣货点距离公式:

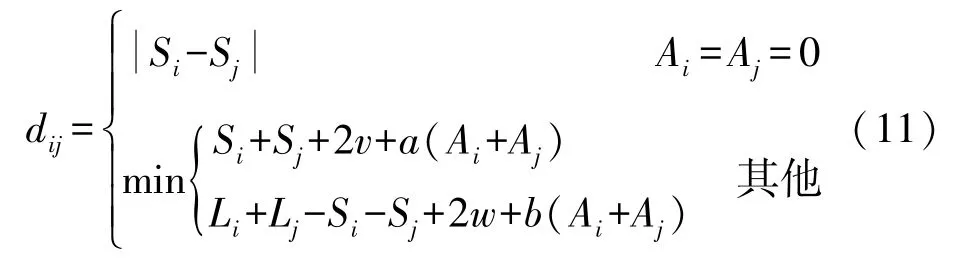
下面对任一拣货点与分拣台之间的距离diz进行分类计算:

(1)P&D 点与分拣台之间的距离公式:

(2)任一拣货点与分拣台之间的距离公式:

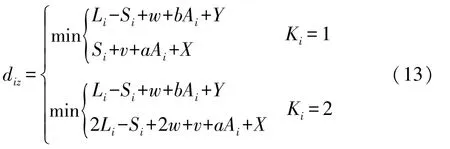
根据仓库布局的对称性,当拣货点在③或④区时,任一拣货点与分拣台之间的距离公式参照拣货点在②或①区的公式。

2.3 “摘果式”拣货方式作业时间的建模

参数设计:

E:客户订单数;

I:货品种类数;

Q:订货数量;

L:订单列表行数;

k:对第k个客户订单进行“摘果式” 拣货(k= {1,2,…,E});

EN:每张客户订单的订货品项数量(在“摘果式”拣货作业中,EN=n≥1,n为一次拣选作业中待拣选点的数目);

ENk:第k个客户订单的订货品项数量(在“摘果式”拣货作业中,ENk=nk,nk为第k次拣选作业中待拣选点的数目);

EQ:每张客户订单的总订货数量;

EQk:第k个客户订单的总订货数量;

TZ:“摘果式”拣货作业总时间;

TZk:第k次“摘果式”拣货作业时间;

TS:“摘果式”拣货作业中对照拣货单花费的总时间;

TSk:第k次“摘果式”拣货作业中对照拣货单花费的时间;

TM:“摘果式”拣货作业中移动花费的总时间;

TMk:第k次“摘果式”拣货作业中移动花费的时间;

TP:“摘果式”拣货作业中拣取放入花费的总时间;

TPk:第k次“摘果式”拣货作业中拣取放入花费的时间;

c1:拣货员的移动系数(平均移动速度的倒数);

c2:对照单据一次所需要的时间;

c3:拣取放入一个商品所需要的时间;

第k次“摘果式”拣货作业时间模型如下:

“往返距离”表示从P&D 点出发到达第一个拣货点的距离以及从最后一个拣货点出发到达P&D 点的距离之和。在“摘果式”全部拣货作业中“往返距离”的平均移动距离D1的表达式:

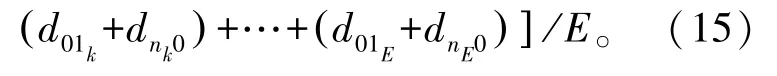
全部拣货作业时在商品间移动的平均距离D2的表达式:

第k次“摘果式”拣货作业发生了一次“往返”以及(ENk-1)次在商品间的移动,第k次“摘果式”拣货作业移动花费的时间表达式:

第k次“摘果式”拣货作业中对照拣货单的次数是ENk次,第k次“摘果式”拣货作业中对照拣货单花费的时间表达式:

第k次“摘果式”拣货作业中拣取放入商品的次数是EQk次,第k次“摘果式”拣货作业中拣取放入花费的时间表达式:

“摘果式”拣货作业总时间模型如下:

2.4 “播种式”拣货方式作业时间的建模

参数设计:

h:对第h种商品进行“播种式” 拣货(h= {1,2,…,I} );

IQ:各商品种类的总订货数量;

IQh:第h种商品的总订货数量;

IK:每个商品种类的订货次数(IK≥1);

IKh:第h种商品的订货次数;

TB1:“播种式”拣货作业第一阶段总时间;

TB2:“播种式”拣货作业第二阶段总时间;

TB:“播种式”拣货作业总时间;

“来回距离”表示从P&D 点出发到达拣货点的距离以及从这个拣货点出发到达分拣台的距离之和。在“播种式”拣货第一阶段的全部拣货作业中“来回距离”的平均移动距离D＇1的表达式:

“播种式”拣货第一阶段的作业时间模型可以通过将“摘果式”拣货作业时间模型中的客户数替换成商品的种类数来得到,见式(22)。其中第一项为移动至货架位置所需的时间,第二项为对照集合单查看商品的时间,第三项为将商品拣取放入集货箱所需的时间。

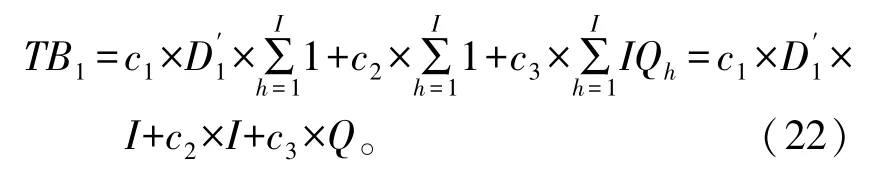
在“播种式”拣货第二阶段的作业中,分货作业是指从P&D 点移动至分拣台,然后将商品从集货箱里面按照客户订单分拣到周转箱,之后再回到P&D 点。因为就处在分拣台各集货箱相邻放置,移动这道工序时由于集货箱间距离太短而忽略不计,所以在分拣一个拣货单的时候只重复进行对照拣货单以及拣取放入这两道工序,中间的移动工序不重复计算。每次分货作业的平均移动距离D3的表达式如下:

“播种式”拣货第二阶段的作业时间模型如式(24),其中第一项为移动至集货箱放置处(即分拣台)所花费的时间,第二项为对照拣货单查看集货箱的时间,第三项为将商品拣取放入周转箱所花的时间。

“播种式”拣货作业总时间模型:

3 基于订单数据分析探讨合适的拣货方式

3.1 “摘果式”拣货与“播种式”拣货总作业时间的比较

为基于订单数据探讨出合适的拣货方式,本研究将“摘果式”拣货作业花费的总时间TZ减去“播种式”拣货花费的总作业时间TB,即用式(20)减去式(25),得到下面表达式。

对式(26)进行分析,因为一般情况下D1＞D2,可得出E、L的值越大,那么式(26)中第一项以及第二项值越大,那么“摘果式”拣货作业花费的时间越多,理想的拣货方式越倾向于选择“播种式”拣货;I、Q的值越大,那么式(26)中第三项以及第四项值越大,那么“播种式”拣货作业花费的时间越多,理想的拣货方式也就越倾向于选择“摘果式”拣货方式。

3.2 “摘果式”拣货与“播种式”拣货第一阶段作业时间的比较

为了对订单数据中的各个要素与拣货方式的选择进行更详细地分析,首先对“摘果式”拣货与“播种式”拣货第一阶段的作业时间进行比较。将“摘果式”拣货总作业时间TZ减去“播种式”拣货第一阶段的作业时间TB1,即用式(20)减去式(22)。因为分拣台距离P&D 点很近,“摘果式”全部拣货作业中“往返距离”的平均移动距离D1与“播种式”第一阶段的全部拣货作业中“来回距离” 的平均移动距离D＇1近似相等,于是令D1＇≈D1。

结合式(27)对E、I、L三个要素进行比较,分析出各订单数据与选择拣货方之间的关系。

(1)当L改变时,E、I、L之间的大小关系如表1所示。

表1 订单数据的分类

类别1:L=E=I

当L=E=I时,即表示每个客户都只订购一种商品,并且每种商品也只有一个客户订购,此类订单若采用“播种式”拣货,不需要进行第二阶段的分货。此时式(27)的第一项值为零,第二项值为零,第三项的值为零,因此式(27)最终值为零。“摘果式”拣货作业与“播种式”拣货作业第一阶段耗时一样,并且“播种式”拣货不需要进行第二阶段,所以当L=E=I时,采用“摘果式”拣货或“播种式”拣货均可。

类别2:L=E＞I

当L=E＞I时,即表示每个客户都只订购一种商品,但多数商品不止一个客户订购。此时式(27)的第一项值为正,第二项值为零,第三项值为正,因此式(27)最终值为正。当L=E＞I时,“摘果式”比“播种式”第一阶段耗时多,再将“摘果式”拣货作业时间与“播种式”拣货总作业时间相比较,将式(26)整理如下:

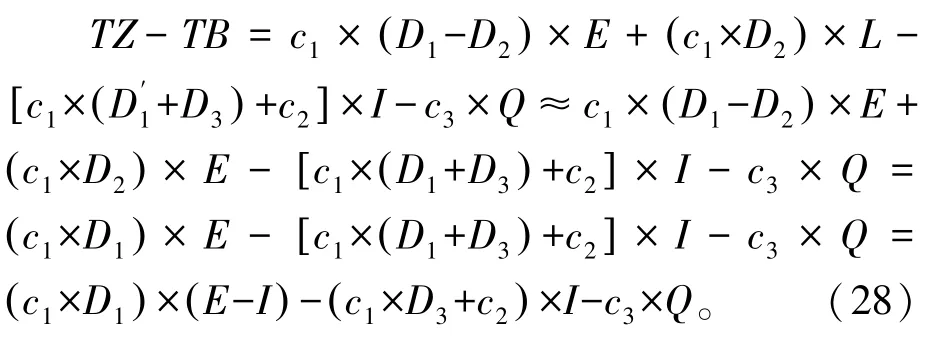
因为分拣台离P&D 点很近,分货作业的平均移动距离D3也会很小。在仓库拣货作业中移动作业最耗费时间,拣取放入商品这一作业所花费的时间较少,对照单据花费的时间更少。当L=E＞I时,式(28)第一项值为正,第二项和第三项值较小,式(28)最终值为正,那么“摘果式”拣货作业花费时间较多,可知此时采取“播种式”拣货方式较好。

类别3:L=I＞E

当L=I＞E时,表示有客户订购不止一种商品,每种商品只有一个客户订购,此类订单若采用“播种式”拣货,不需要进行第二阶段的分货。此时可以将式(27)整理如下:

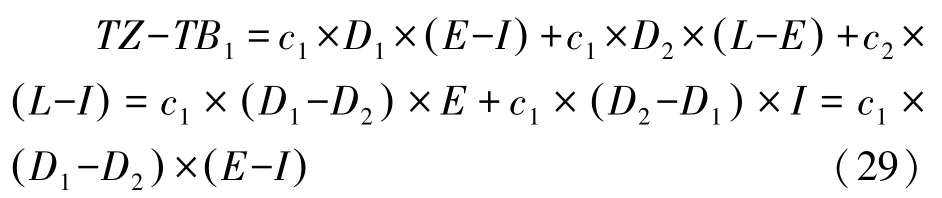
由式(29)可知,当L=I＞E时,(E-I)＜0,所以式(29)最终值为正或者负取决于D1与D2的大小关系,以下分为类别3.1 和类别3.2 详细讨论D1与D2的大小对式(29)的影响。

类别3.1:L=I＞E,D1＞D2

当L=I＞E、D1＞D2时,(TZ-TB1)＜0,式(29)值为负,“摘果式”比“播种式”第一阶段耗时少,因此采用“摘果式”拣货方式较好。

类别3.2:L=I＞E、D1＜D2

当L=I＞E,D1＜D2时,(TZ-TB1)＞0,式(29)值为正,“摘果式”比“播种式”第一阶段耗时多,并且此时不需要进行“播种式”拣货的第二阶段,因此采用“播种式”拣货方式较好。

类别4:L＞E、L＞I

当L＞E、L＞I时,表示客户订购不止一种商品,每种商品不止一个客户订购。此时式(27)的第二项值为正,第三项的值为正,第一项值是正或负需要比较E、I两者之间的大小得出。因此,对此类情况继续进行如下分析。

类别4.1:L＞E＞I

当L＞E＞I时,式(27)的第一项值为正,第二项值为正,第三项的值为正,因此式(27)最终值为正。由此可知当L＞E＞I时,“摘果式”比“播种式”第一阶段耗时多。再将“摘果式”拣货作业时间与“播种式”拣货总作业时间相比较,将式(26)整理如下:

当L＞E＞I时,式(30)第一项值为正,第二项值为正,第三项和第四项值很小,式(30)最终值为正,那么“摘果式”拣货作业花费时间较多,可知此时采取“播种式”拣货方式较好。

类别4.2:L＞E=I

当L＞E=I时,式(27)的第一项值为零,第二项值为正,第三项值为正,因此式(27)最终值为正。由此可知当L＞E=I时,“摘果式”比“播种式”第一阶段耗时多。再将“摘果式”拣货作业时间与“播种式”拣货总作业时间相比较,将式(26)整理如下:

当L＞E=I时,式(31)第一项为正,第二项和第三项值很小,式(31)最终值为正,那么“摘果式”拣货作业花费时间多,可知此时采取“播种式”拣货方式较好。

类别4.3:L＞I＞E

当L＞I＞E时,式(27)的第一项值为负,第二项值为正,第三项值为正,此时无法判断式(27)最终值的正负。再将“摘果式”拣货作业时间与“播种式”拣货总作业时间相比较,将式(26)整理如下:

要得出式(32)最终值的正负,应该主要比较式(32)中第一项与第二项值的大小,即将各项移动所花费的时间作比较,下面分为类别4.3.1 和类别4.3.2 分别对移动距离大小做比较,分析出式(32)最终值的正负。

类别4.3.1:L＞I＞E、D1＞D2

当L＞I＞E、D1＞D2时,式(32)每一项值均为正,虽然(L-E)＞(I-E),但两者之间的差值不大,并且D1＞D2,此时第一项减去第二项值为负,后面两项值均很小,那么此时式(32)最终值为负,“播种式”拣货作业花费时间较多,此时采用“摘果式”拣货方式较好。

类别4.3.2:L＞I＞E、D1＜D2

当L＞I＞E、D1＜D2时,式(32)每一项值均为正,因为(L-E)＞(I-E)且D2＞D1,此时第一项减去第二项后,值为正,第三项以及第四项值很小,那么这时式(32)最终值为正,“摘果式”拣货作业花费时间较多,此时采用“播种式”拣货方式好。

3.3 结论分析

本研究对订单数据中的四个要素:客户数E、商品的种类数I、订货数量Q以及订单的列表行数L进行分析比较,对订单数据进行分类,分析各要素对拣货方式选择的影响和各种类别下哪一种拣货方式耗时较短。总体来看,E、L的值越大,理想的拣货方式越倾向于选择“播种式”拣货;I、Q的值越大,理想的拣货方式也就越倾向于选择“摘果式”拣货方式。

根据以上分析,将E、I、L三种要素以及距离D1、D2的比较进行整理,得到理想拣货方式有八种类别组合,如表2所示。

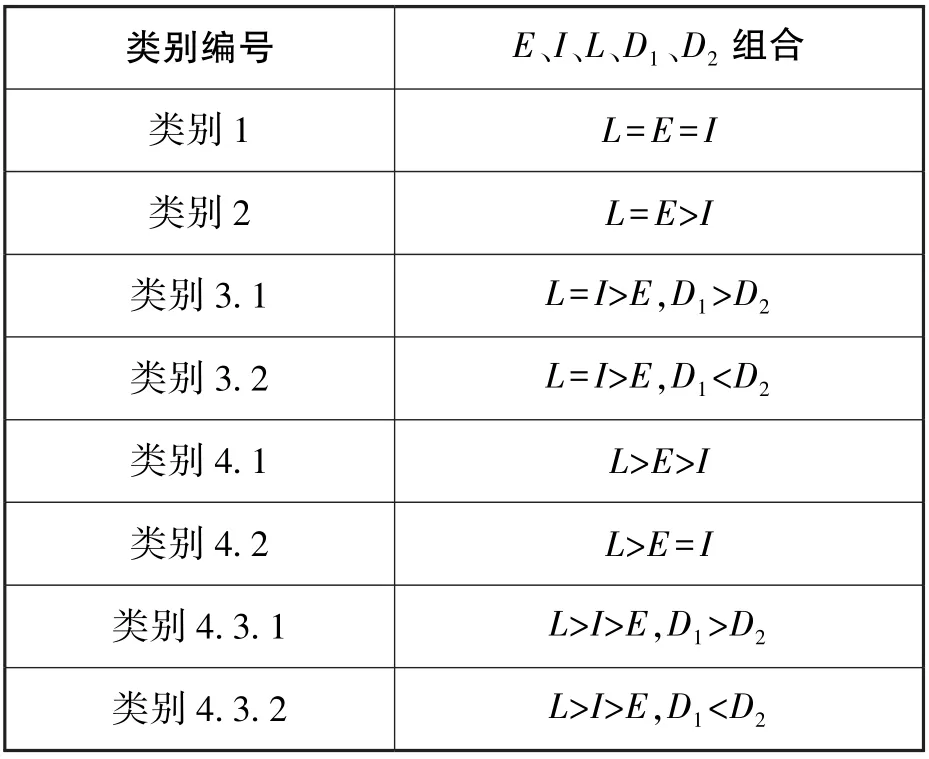
表2 各类别下E、I、L 三种要素以及距离D1、D2 的组合

对这八种组合下对应的理想拣货方式的选择进行整理,结果如表3所示。

表3 理想拣货方式的选择

4 总结与展望

本研究在鱼骨型仓库布局下基于订单数据中的四个要素(客户数E、商品种类数I、订货数量Q和订单列表行数L),对拣货方式的选择进行了定量的分析。文章首先对两种拣货方式的作业流程进行了分析,得出拣货过程中较花费时间的工序是对照单据查看待拣商品、移动以及拣取放入商品。无论哪种模型,移动花费时间的占比比较大,对照单据查看待拣商品和拣取放入商品花费时间较少。基于鱼骨型仓库得出移动距离模型,随后基于订单数据对所花费的时间进行建模,得出各拣货方式的作业时间模型。将各拣货作业时间进行比较,得出理想拣货方式的选择与订单数据中四个要素之间的关系。总体来看E、L的值越大,理想的拣货方式越倾向于选择“播种式”拣货;I、Q的值越大,理想的拣货方式越倾向于选择“摘果式”拣货方式。本研究是基于鱼骨型仓库进行的分析探讨,若要研究其他类型仓库下拣货方式的选择,可以直接替换成所研究仓库的距离公式。

本研究对多处时间以及距离做出了近似估计,缺乏数据的验证。此外,物流配送中心在实际运营时,也会遇到加急订单,需要单独进行拣货分析。

将来可以带入仓库订单数据对上述分析进行验证。对仓库里面的特殊订单作进一步分析,单独确定其拣货方式选择情况。现在仓库更多地趋向于无人化、智能化,未来可以基于智能化的仓库来确定拣货方式的选择。