基于犹豫模糊语言环境的投资组合优化研究

周晓光, 何 欣, 王晓岭

(北京科技大学 经济管理学院,北京 100083)

0 引言

投资组合优化模型自提出以来一直备受关注，其核心思想是用均值来衡量收益，用方差来衡量风险。早期的投资组合模型大多采用随机变量描述资产的收益率，但概率论基于先验数据进行研究决定了随机变量无法准确刻画瞬息万变的金融市场。此外，金融资产的收益在很大程度上依赖于投资者个人的主观判断，即使是金融专家也难以进行准确的评价。因此，学者们提出了基于模糊理论的投资组合优化模型[1,2]。

2009年，Torra和Narukawa提出犹豫模糊集[3]。随后，Zhou等[4]提出了犹豫模糊集(其隶属度是一个不确定的值)下的投资组合选择和风险度量方法，为犹豫模糊理论在投资组合选择中的应用奠定了基础。犹豫模糊变量的不确定程度都是基于数值的表示，而在实际过程中，投资者往往倾向于使用定性的自然语言来表达他(她)对金融产品的看法。同时，越来越多的金融产品及其衍生品进入市场交易，投资者受自身对金融市场了解程度的限制，也并不能准确地给出犹豫模糊变量的隶属度，而是在多个自然语言评价中徘徊[5]。

Rodriguez等[6]提出的犹豫模糊语言术语集不仅可以使用自然语言对金融产品进行评价，刻画投资者的不确定程度，还可以避免自然语言在决策过程中信息的丢失，从而得到更为准确的评价结果[7]。直觉模糊二元语义在企业价值评估、项目选择等多个领域取得了应用[8.9]，犹豫模糊语言也逐渐成为学者研究的热点[10]。本文基于犹豫模糊语言环境研究投资组合优化问题，以通过资金的最优分配实现产品收益与风险之间的均衡。

1 基本理论

定义1[11]设S={Sα|α= -τ, …, -1, 0, 1, …,τ}为语言术语集，ai∈A,i=1,2,…,N，A上的犹豫模糊语言集HS的数学形式为

HS={}ai∈A}

(1)

其中：hS(ai):A→S指元素ai∈A映射到集合X⊂A的可能隶属度，hS(ai)是语言术语集S中一系列连续的可能取值，且hS(a)={sφl(ai)|Sφl(ai)∈S,l=1,2,…,L};φl∈{-τ,…,-1,0,1,…,τ}为语言术语Sφl(ai)的下标，L(ai)为hS(ai)中语言术语的个数。为简化起见，称hS(ai)为犹豫模糊语言数(Hesitant Fuzzy Linguistic Element, HFLE)，HS为语言术语集S上的全部犹豫模糊语言数的集合，即犹豫模糊语言集(Hesitant Fuzzy Linguistic Set, HFLS)。

定义3[12]设S={Sα|α= -τ,…,-1,0,1,…,τ}为语言术语集，θα∈R+是语言术语Sα对应的语义，语言尺度函数为从Sα到θα的映射，即g:Sα→θα，其中g是关于下标α的单调函数，且g(Sα)∈[0,1]。

定义4[13]犹豫模糊语言数的犹豫度函数，以其对应的语言术语集中元素的个数L为基础，定义为一个严格单调递增的凸函数，如下所示:

(2)

显然，犹豫模糊语言数的长度越长，即语言术语集中的元素越多，犹豫度越大。

2 基于犹豫模糊语言集的投资组合优化模型

2.1 基于犹豫模糊语言的股票得分评价方法

本文以股票市场为例来说明犹豫模糊语言环境下的投资组合优化问题。在投资过程中，投资者常面临的一个问题是，选择哪些股票进行投资以实现预期投资组合收益的最大化。这其中涉及到的一个很重要的环节就是投资者要对证券市场上的股票进行评估。大多数投资者面临不同的投资抉择时，第一个考量标准往往是“这只股票会涨还是会跌？”进而投资者才会根据对股票涨跌的预判决定是否将资金投入该股。

本文通过改进Score-HeDLiSF[14]方法，提出基于犹豫模糊语言的二级投资组合评价系统，对股票xi(i=1,2,…,n)进行评价，具体步骤如下：

步骤1建立犹豫模糊语言投资组合评分系统的初级评价语言术语集LTS，表示为S={Sα|α=-τ,…,-1,0,1,…,τ}，并通过语义值函数对每一语言术语Sα进行量化评分。鉴于初级评价是投资者对股票“是否看好”的主观陈述，随着语义程度的加剧，其初级自然语言评价会呈现越来越严谨的用语习惯，即投资者给出“极其看好/不看好”的初级评价一定会较“有一些看好/不看好”更为谨慎，也就是说初级相邻语义间隔以S0为分界向左、右两边逐渐减小，即随着语义程度的加重，相邻语言尺度函数值之差呈递减趋势，因此本文初级评价语言术语采用相邻语义间隔递减的单调递增函数[16]，表达式如下:

(3)

其中，ζ表示股票看跌时对应的投资者的风险态度参数，ξ表示股票看涨时对应的投资者的风险欲望参数。

本文主要研究同一投资者就股票看涨、看跌评价语义关于S0对称的情况，即ζ=ξ且满足g(Sα+1)-g(Sα)=g(S-α)-g(S-α-1)。需要指出的是，若ζ=ξ的值小于0.5，对应的投资者趋向于保守型，其相邻语言尺度函数值之差相对较大，即g(Sα+1)-g(Sα)相对较大，原因是保守型投资者对于“极其看好”的股票，语义函数值的赋值要求相对高于激进型投资者；对于“极其不看好”的股票，语义函数值的赋值要求低于激进型投资者，故其差值相对较大。若ζ=ξ恰好等于0.5，对应的投资者近似于稳健型。若ζ=ξ的值大于0.5，对应的投资者趋向于激进型，其相邻语言尺度函数值之差相对较小。

步骤2对备选股票进行关于涨跌趋势的初级自然语言评价，利用文本自由语法GH[8]将每只股票的初级自然语言评价转换为语言表达式ll。

步骤3通过转换函数[8]将语言表达式ll转化为犹豫模糊语言数hS(xi)，得到关于初级评价的犹豫模糊语言集HS。

步骤4通过式(2)计算初级评价犹豫模糊语言数hS(xi)的犹豫度HD(hS)，进一步求出关于该股涨跌趋势的量化得分，如下所示。

(4)

(5)

步骤6对每只股票进行投资可能性判断，利用文本自由语法GH将对该股的二级自然语言评价转换为语言表达式ll′。

(6)

步骤9计算股票经过二级投资组合评价犹豫模糊语言系统得到的综合评分，计算公式如下：

(7)

2.2 投资组合优化模型

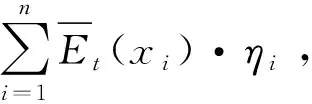
(8)

该投资组合的风险可表示为：

(9)

(1)优化模型

本文以收益最大作为犹豫模糊语言投资组合的优化目标，将风险控制在可接受的最大风险Dmax之内作为约束条件，模型如(10)式所示。以Emin为约束条件，以风险最小化为目标的犹豫模糊语言投资组合优化模型(11)本文不作赘述。

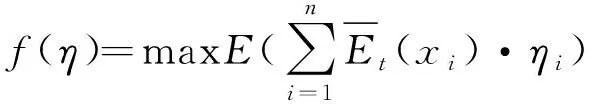
(10)

(11)

(2)不同类型投资者的方差临界值Dmax的求法

在实际投资过程中，不同风险偏好的投资者由于自身的性格、文化背景和对金融产品的认知不同，对风险的承受能力是不一样的，在优化模型中体现为Dmax取值的不同。激进型投资者Dmax最高，稳健型次之，保守型最低。

本文采用三等分法[2]求解不同类型投资者对应的Dmax，如图1所示。假设最大风险临界值Dmax的波动范围为[minD,maxD]。

A.设激进型投资者对应的最大风险临界值Dmax为D1，则D1=maxD；

B.设稳健型投资者对应的最大风险临界值Dmax为D2，则D2=2/3(maxD-minD)；

C.设保守型投资者对应的最大风险临界值Dmax为D3，则D3=minD+1/3(maxD-minD)。

图1 不同风险偏好投资者Dmax的三等分示意图

(3)maxD和minD的求法

HFLE收益最大化投资组合优化模型对应的最大风险临界值Dmax，在采用三等分法求解释时，需要确定minD和maxD。本小节以犹豫模糊语言投资组合的方差为优化目标，通过求解优化模型(12)，得到犹豫模糊语言投资组合方差的极值(即maxD和minD)。

(12)

3 数例仿真

3.1 基于犹豫模糊语言的投资组合优化过程

根据前文介绍的犹豫模糊语言二级投资组合评价系统以及提出的犹豫模糊语言投资组合优化模型，现将犹豫模糊语言环境下的投资组合优化过程总结如下：

步骤1建立犹豫模糊语言的股票得分评价系统的初级、二级评价语言术语集LTS。

步骤2根据式(3)和式(5)分别计算犹豫模糊语言投资组合评分系统的初级、二级评价语言术语的语义值。

步骤3分别对股票的涨跌情况及感兴趣程度进行判断，利用文本自由语法和转换函数得到相应的犹豫模糊语言数。

步骤4利用基于犹豫模糊语言的二级投资组合综合评价系统对每一只股票进行打分。

步骤5根据模型(12)计算[minD,maxD]。

步骤6采用三等分法对不同风险偏好的投资者确定模型(10)中的参数Dmax。

步骤7根据投资者实际情况，构造收益最大化或风险最小化犹豫模糊语言投资组合优化模型。

步骤8求出最优投资比例ηi。假设总投资金额为K，则每只股票的投资金额为Kηi。

3.2 基于犹豫模糊语言的投资组合优化数例仿真

为说明本文提出的犹豫模糊语言得分评价系统及优化模型的合理性和有效性，现将上述投资组合优化过程以数例进行说明。假设有5只股票{x1,x2,x3,x4,x5}可供选择，每只股票投资比例表示为{η1,η2,η3,η4,η5}，且满足，投资者现有资金总额为100000元。本文以保守型投资者为例，并假设该投资者以收益最大化为投资目标。现采用基于犹豫模糊语言的投资组合优化过程进行求解，具体过程如下所示：

步骤2根据式(3)和式(5)分别计算犹豫模糊语言投资组合评分系统的初级及二级评价语言术语的语义值。考虑到投资者的风格为保守型，因此令ζ=ξ=0.2，且τ=3，τ′=6。

步骤3投资者分别对股票的涨跌情况及感兴趣程度进行个人判断，并给出相应的自然语言评价。利用文本自由语法和转换函数得到相应的犹豫模糊语言数，其中初级犹豫模糊语言数转化结果如表1所示，二级犹豫模糊语言数转化结果如表2所示。

表1 初级犹豫模糊语言数转化过程

表2 二级犹豫模糊语言数转化过程

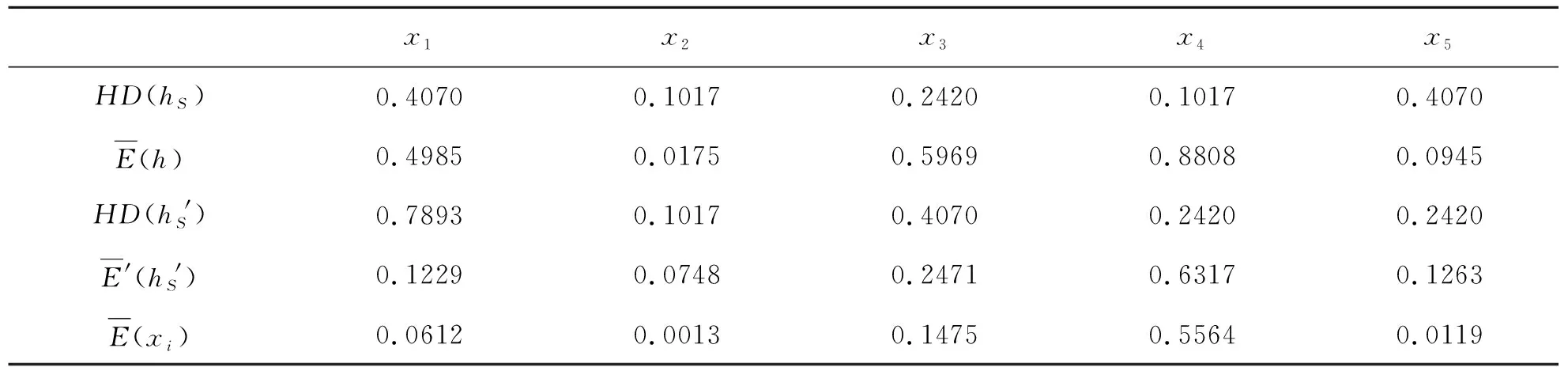
表3 犹豫模糊语言投资组合评价系统得分计算过程

步骤4首先通过式(2)计算每一级犹豫模糊语言数的犹豫度，然后根据式(4)和式(6)分别计算初级及二级评价的量化得分，最后根据式(7)计算得出每只股票的犹豫模糊语言投资组合综合评分，计算结果如表3所示。

步骤5由于投资者以收益最大化为投资目标，故以最小风险为约束。根据模型(11)计算[minD,maxD]，代入数据可得非线性优化模型(13)。利用Matlab对其进行求解，得到投资者犹豫模糊语言投资组合方差的极大、极小值，分别为maxD=0.4773,minD=0.00003。

f(η)=maxD或minD

(13)

步骤6根据三等分法求出投资者的最大风险临界值Dmax，并设为D3，D3=minD+1/3(maxD-minD)=0.1591。

步骤7鉴于投资者以收益最大化为投资目标，故选择模型(10)求解投资组合的最优解，犹豫模糊语言投资组合优化模型代入数据如下所示：

f(η)=maxE

(14)

步骤8采用Matlab求解上述非线性优化模型，得到最优投资比例为η1=η2=η5=0，η3=0.6575，η4=0.3425，即最优投资组合为：对第3只股票投资65750元，对第4只股票投资34250元。

3.3 仿真结果分析

上述研究基于保守型投资者，如果更改初级评价语义值函数的风险态度参数ζ和风险欲望参数ξ值，可以求出不同风险偏好投资者的最优投资比例。例如，对稳健型投资者，令ζ=ξ=0.5；对激进型投资者，令ζ=ξ=0.7。

不同风险偏好的投资者对五只股票总得分如图2所示，三类投资者对五只股票的犹豫模糊语言评价得分均满足x4>x3>x1>x5>x2，符合对五只股票的自然语言评价。具体地，对于x4其初级自然语言评价为“至少还不错”，其二级自然语言评价为“很想买”，因此，x4犹豫模糊语言评价得分最高。在相对看好的股票中，即对于股票x1、x3和x4，保守型投资者经过犹豫模糊语言评分系统得到的分数最高，而激进型投资者得分最低，这是因为厌恶风险的投资者对于股票选择更为慎重，同时其谨慎的投资态度导致只有得分相对较高的情况下，才会对这只股票予以好评。反之，对于不看好的股票x2和x5，保守型投资者只有在得分极低的情况下，才会认定这只股票不好。

通过对三种类型的投资组合优化模型进行求解，三类投资者的最优投资比例如表4所示。三类投资者都主要将资金投入到了x3和x4，而在x1、x2和x5未投资，其中保守型投资者倾向于x3，而激进型则倾向于x4，这是因为保守型投资者会适当牺牲利益以换取相对较小的投资风险，而激进型投资者则以尝试更大的风险为代价追求高额的利润。需要指出的是，本文提出的模型对于不太看好的股票(如本例中的x2和x5)的资金分配也同样可以实现优化配置，在实际投资中，也可能会出现对看跌的股票如何分配资金以图反弹获利，利用本文提出的优化模型亦可求解。

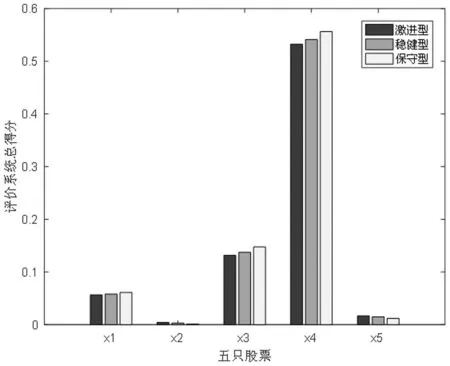
图2 三种不同类型投资者的评分图

表4 三种不同类型投资者在五只股票上的投资比例及收益与风险极值

图3给出了三种类型投资者对应的犹豫模糊语言投资组合maxE及对应所需承受的风险D值。可以看到不同类型投资者在取到最优解时，对应的投资组合方差值均取到了最大临界值，即D1=0.4567，D2=0.3097，D3=0.1591。这是因为在追求收益最大化的同时，势必会增加投资风险。此外，激进型投资者所获得的收益及承担的风险是最大的，保守型投资者最小。这验证了高收益伴随着高风险，降低风险一定是以牺牲期望利润为前提的。

4 结论及展望

本文在根据犹豫模糊语言对金融产品进行二级综合评价的基础上，建立了犹豫模糊语言投资组合优化模型，针对激进型、稳健型和保守型三种不同类型的投资者分别求出最优投资组合方案。最后采用数值仿真对不同类型的投资者进行了比较分析，验证了所提出的犹豫模糊语言投资组合优化模型的合理性和有效性。未来进一步的研究方向如下：

(1)面对复杂多变的金融市场，理性的投资者如若将资金投入到看跌的股票上，一定是认为这只股票在跌到一定程度后，就会触底反弹。对于这种情况，犹豫模糊语言投资组合评价系统如何运作？如何进行资金的最优分配以实现收益与风险的均衡？

(2)本文研究的是一位投资者对n只股票进行的评价，如果对每只股票从m个维度进行综合评价，如何建立犹豫模糊语言投资组合优化模型？