双目标消防救援站选址模型的元胞阴阳平衡优化算法
2022-02-08许秋艳
许秋艳, 马 良, 刘 勇
(1.上海理工大学 管理学院,上海 200093; 2.盐城工学院 信息工程学院,江苏 盐城 224051)
0 引言
消防救援站布局规划是典型组合优化问题,属于运筹学中NP难问题[1]。严珍珍等将消防救援站选址问题表示为以成本最小为目标的集合覆盖问题,并采用带精英策略的蚁群算法进行求解[2]。卢厚清等以覆盖面积最大,利用连续网空间覆盖模型处理消防救援站选址问题,并设计改进模拟退火算法进行求解[3]。Wang等采用集合覆盖模型构建消防救援站选址模型,并采用ARON工具箱求解模型[4]。Chen等利用最大覆盖模型构建消防救援站选址模型,并采用地理信息系统软件进行站点布局的求解[5]。考虑到问题复杂性,越来越多研究人员将多目标优化引入到消防救援站选址布局中。Yang构建成本最小和最远距离最短的双目标消防救援站选址模型,采用基于遗传算法的求解方法[6]。Yao等将P-中值选址模型和最大覆盖模型相结合,构建多目标消防救援站选址模型,并设计启发式算法求解非劣解[7]。王宁等考虑消防救援站的平衡性与效益,建立消防站布局的多目标覆盖模型,并采用Pareto强度进化算法求解模型[1]。
上述多目标优化研究为消防救援站布局规划提供了更好解决方案,但是对时间这一重要指标研究的较少。我国提出了15分钟消防标准,如何将时间因素引入到多目标消防救援站建模中是必须要解决的问题。在选址时还要考虑需求点人口数量和潜在火灾风险等级。此外,根据最新发布的《城市消防站建设标准》,明确要求控制成本。因此,本文将构建考虑时效性和经济性的双目标消防救援站布局规划模型,并将上述其它因素纳入到建模中。
采用多目标优化模型处理消防救援站选址问题更加合理,但是加大了模型求解难度。许多研究是将多目标消防救援站选址问题转化为单目标问题进行求解,无法得到真正非劣解[8]。智能优化算法是求解该类问题常用方法。典型算法有多目标遗传算法、多目标微粒群优化算法、多目标蚁群优化算法等[8]。但是这些算法求解非劣解的效率需要提升,另外这些算法也无法直接用于多目标消防救援站选址模型的求解。该选址问题属于多目标组合优化问题,而多目标组合优化问题比多目标连续优化问题的求解更加困难,缺少实用算法。
为有效求解该问题,本文在阴阳平衡优化算法[9](Yin-Yang pair optimization, YYPO)和元胞自动机基础上,设计元胞阴阳平衡优化算法(cellular Yin-Yang pair optimization,CYYPO)进行求解。YYPO算法是Punnathanam等在2016年提出的一种新型智能优化算法,其优化原理来自中华传统文化中的阴阳学说。算法期望在哲学原理上实现阴阳平衡,进而实现算法全局探索和局部开发的均衡。但是基本阴阳平衡优化方法全局搜索性能强,而局部搜索性能弱[9]。为有效求解该问题,本文将元胞自动机引入到基本阴阳平衡优化算法中,提高算法局部优化能力。元胞自动机由冯诺依曼提出,是在时间与空间都离散的一种动力学模型。根据其原理,重复简单计算规则就能刻画复杂系统行为,多次进行邻域的交互作用就能提高算法局部搜索能力[10]。个体在阴阳平衡优化算法搜索空间进行全局寻优,以搜索到尽可能多的包含非劣解的区域;同时也在元胞空间利用演化规则对这些区域进行局部优化,以搜索到Pareto最优解。此外,利用算法交流机制实现优化信息在算法的搜索空间和元胞空间内的共享,每个个体动态调整搜索行为,引导整个群体不断向Pareto最优前端逼近。实验验证了所构建选址模型和求解算法的可行性与有效性。
1 考虑时效性和经济性的双目标消防救援站选址模型
1.1 问题描述
根据我国15分钟的消防标准,在设施点布局规划时要考虑时效性。火灾危险等级可分为四个等级,分别是轻微,中等,严重和极高。结合火灾风险等级,引入救援响应时间的概念[11]。轻微,中等,严重和极高四种火灾风险等级的响应时间分别为12~15分钟;8~12分钟;5~8分钟和4~5分钟。结合上述分析,给出时效性评价函数定义:
(1)
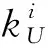
借鉴覆盖水平函数概念[11],函数f(tij)可以是线性或者非线性函数。本文采用Sigmoid函数,表达式如下:
(2)
1.2 模型构建
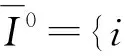
构建的消防救援站选址模型为:
max∑i∈I∑j∈Jwig(tij)xij
(3)
min∑j∈Jcjyj
(4)
s.t. ∑j∈Jyj=p
(5)
xij≤yj,∀i∈I,j∈J
(6)
(7)
(8)
yj∈{0,1},∀j∈J
(9)
xij∈{0,1},∀i∈I,j∈J
(10)
其中,式(3)表示考虑时效性的综合覆盖水平最大;式(4)表示消防救援站总建设成本最小;式(5)表示消防救援站建设数量;式(6)表示在备选点j建立消防救援站时,才能为需求点i提供服务;式(7)和(8)要求每个需求点i被分配给一个消防救援站提供服务,当需求点i时效性函数g(tij)为0时,将其分配到一个行车时间最短的消防救援站;式(9)和(10)表示决策变量取值范围。
针对该模型NP难问题特征,本文在阴阳平衡优化算法基础上,设计元胞阴阳平衡优化算法来求解该问题。
2 阴阳平衡优化算法
阴阳平衡优化算法YYPO在具体实现时,包含利用超球体和归档集的两个解更新阶段[9]。受太极图的启示,算法在1为半径的超球体内,分别以P1与P2两个点作中心,δ1与δ2作步长进行解的更新。由于这两个点采用同样的解更新策略,为简单起见,令P代表P1或者P2,δ代表δ1或者δ2。在生成新解前,首先生成2D(D代表变量维数)个同样的点P。解的更新方法共分为1维更新和D维更新两种,
方法如式(11)和(12)所示:
(11)
(12)
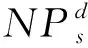
算法基于等概率原则选择上述两种方法中的一种进行解的更新。此外,从P1产生的2D个点中,选择适应度值最优点替换P1。算法对P2也进行相同操作。
算法采用精英保留策略,在每次超球体内的解更新之前,会将P1和P2储存到名为archive的归档集内。每间隔I次迭代,算法就进入基于归档集的解更新阶段,将采用archive中的2I个点对当前的P1与P2进行更新。首先,在archive中选择最优点,如果该点优于点P1则将这两点互换。然后,对点P2也采用同样更新策略。此外,在该阶段算法还要在Imin和Imax之间重新生成参数I,并且对搜索半径δ1与δ2进行更新,具体计算方法如下:
δ1=δ1-(δ1/α)
(13)
δ2=δ2+(δ2/α)
(14)
其中,α表示缩小/扩大因子。
算法反复进行上述两种解更新方法,直到满足停止条件。
3 元胞阴阳平衡优化算法
3.1 元胞自动机
元胞自动机是描述系统存在和演化的离散动态系统。元胞、元胞空间、邻居和演化规则是其四个基本组成部分。以下给出元胞自动机在算法中的具体实现形式。
定义1元胞及元胞空间
令集合C=(c1,c2,…,cj,…,cN),N表示备选消防救援站数量;cj∈{0,1},若cj=1,表示在第j个备选点建消防救援站,若cj=0,表示未在第j个备选点建消防救援站。集合C中cj所有可能取值的组合构成的集合定义为元胞空间,并用L={CellX=(c1,c2,…,cj,…,cN)|cj∈{0,1}}表示。一个组合CellX是一个元胞。
定义2穆尔邻居类型NMoore={CellY|diff(CellY-CellX)≤r,CellX,CellY∈L}。其中,diff(CellY-CellX)≤r是两个元胞间的差异。
定义3演化规则
根据元胞邻居的类型计算元胞及其邻居的每个目标函数值,并根据偏序关系进行比较,选择最好的Pareto最优解集。
定义4偏序关系
在处理多目标优化问题时,采用偏序关系同时考虑Pareto解集的收敛性和分布性。首先采用非支配排序法分析Pareto解集的收敛性,将所有搜索个体分成不同层级。目前没有被其它任何个体所支配的个体为非支配的(Pareto-占优的),定义该个体的rank为1,所有这些非支配的个体集合成为第一层Pareto-占优集合;然后对剩下的个体继续按照上述方法生成第二层Pareto-占优集合。以此类推,将每个寻优个体都进行排序[8]。
除考虑Pareto解集收敛性外,还需考虑其分布情况。采用拥挤距离分析个体之间聚集情况[8]。设P[n]distance为个体n的拥挤距离,P[n].k为个体n的第k个目标函数值。当有r个目标函数时,第n个个体拥挤距离为
(15)
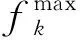
通过上述计算,每个搜索个体都有排序值和拥挤距离两个特征值。在此基础上,定义个体n和个体m的偏序关系:当P[n]rank
3.2 候选解的表示
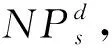
本文采用V型转换函数进行处理:
(16)
(17)
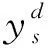
在得到模型中的选址变量后,根据各个需求点到备选消防救援点的行车时间,将每个需求点分配到离其最近的消防救援点,就得到了模型中的分配变量。该方法突出了时效性相对于经济性的重要性。
需要指出的是,在生成选址变量时,可能会产生不可行解,需要对此进行修复。当消防救援站建设数量超过预设值时,根据偏序关系,每次选择排名最后的个体对应的已建备选点进行关闭,直到备选设施数满足规定数量要求。当消防救援站建设数量低于预设值时,同样根据偏序关系,每次选择排名第一的个体对应的未建备选点,直到备选设施数等于规定数量。
因此,利用上述候选解的表示方式,就可以直接生成该问题的可行解。
3.3 算法流程
综上所述,给出求解新模型的元胞阴阳平衡优化算法的主要计算步骤:
步骤1随机产生两个初始点P1和P2,初始化搜索步长δ1和δ2以及更新频率I;
步骤2根据偏序关系,若点P2优于点P1,则互换这两个点取值和步长;
步骤3将点P1和P2保存到归档集;
步骤4在基于超球体的解更新阶段,按相同概率原则分别利用P1与P2进行优化搜索;
步骤5根据演化规则,元胞在邻居范围内进行演化,并根据偏序关系,保存最好的Pareto最优解;
步骤6若迭代间隔数和更新频率I相等,则进入基于归档集的解更新阶段,转步骤7;否则,转步骤8;
步骤7根据偏序关系,利用归档集对当前P1和P2进行更新,调整两个步长δ1和δ2,重新生成更新频率I;
步骤8若迭代次数达到预设最大值,算法停止,输出最终的Pareto解集;否则,转到步骤2。
4 数值实验
通过实验测试新模型和新算法的可行性和有效性。首先给出算例及其计算结果;然后比较新模型和最大覆盖模型的选址方案;最后将新算法和5种智能优化方法的计算性能进行比较。
4.1 算例和计算结果
现有60个区域(分别用1~60进行标号),政府计划在50个备选点(分别用1~50进行标号)中选择3个点建造消防救援站。火灾风险等级极高的需求点有1、9、13、14、22、23、29、31、34、35、42、52,对应人口数各为15.36、15.22、14.83、12.81、13.09、16.25、12.02、18.78、19.86、18.98、18.75、18.62(人口单位:万);火灾风险等级严重的需求点有3、27、32、33、36、43、46、53、54、56、57、59、60,对应人口数各为11.46、14.56、11.73、17.71、10.09、16.67、18.34、14.57、16.81、19.30、17.02、18.79、14.08;火灾风险等级中等的需求点有2、7、8、11、17、39、40、41、47、48、49、50、55,对应人口数各为7.95、7.00、9.03、9.48、6.86、8.35、11.61、8.53、11.15、9.58、6.43、10.83、10.43;火灾风险等级轻微的需求点有4、5、6、10、12、15、16、18、19、20、21、24、25、26、28、30、37、38、44、45、51、58,对应人口数各为5.21、5.86、4.97、7.71、1.64、3.39、5.09、1.59、4.83、2.28、2.01、8.49、5.99、6.39、4.69、5.70、3.37、2.22、4.49、8.47、4.45、3.16。(限于篇幅,需求点到救援站备选点行车时间和备选点建设成本数据请和第一作者联系)。
采用CYYPO算法求解上述算例。
算法参数设置为Imin=1,Imax=5,α=25。此外,两个搜索步长δ1和δ2初值设为0.5,为预防δ2无限制增加,越过算法搜索空间,设其上限为0.75。穆尔邻居参数r取1。最大函数评价次数为40000次。实验在IntelCorei53.00GHz、8G内存的计算机上进行,软件为Windows10和MatlabR2019a。
CYYPO算法共求出14组Pareto最优解。这里,仅给出第2个Pareto最优解对应的分配方案。选择的消防设施点为20、24和32。分配给20号消防设施点的需求点有4、7、13、15、25、26、31、33、34、41、44、48、52、56、57和59;分配给24号消防设施点的需求点有1、6、8、9、10、12、14、17、19、20、21、22、23、27、28、29、32、35、36、40、42、43、45、46、54、55和60;分配给32号消防设施点的需求点有2、3、5、11、16、18、24、30、37、38、39、47、49、50、51、53和58。时效性函数值为1的需求点包括1、3、5、6、7、8、9、10、11、12、13、14、15、16、18、22、23、25、26、28、29、30、31、32、33、34、35、37、38、39、41、42、43、46、48、49、50、51、52、54、55、56、57和60;其它需求点(按标号顺序)的时效性函数值分别为0.7540、0.5572、0.4551、0.7089、0.7271、0.2176、0.5150、0.7790、0.7958、0.8100、0.7990、0.3015、0.8038、0.7958、0.7958、0.6637和0.7685。
从上述结果可以发现,所有需求点的时效性函数值均大于0,说明消防站可以在规定时间内到达救援现场。所有需求点时效性函数平均值为0.9009,时效性函数值为1的需求点比例为72%。火灾风险等级为极高、严重、中等和轻微的四种需求点时效性函数值平均值分别为1、0.9362、0.8856和0.8349,时效性函数值为1的比例分别为100%、69%、62%和63%。在建模时引入时效性函数,能够从整体考虑各种类型需求点救援时间要求,尽量实现消防站规划的系统最优。下文将所建模型和最大覆盖模型的计算结果做比较,说明新模型的有效性。
4.2 模型对比
本文构建的双目标消防救援站选址模型是最大覆盖模型的一种扩展形式,将从综合覆盖水平、建设总成本和时效性函数值三方面对这两种模型进行比较。最大覆盖模型采用Matlab优化工具箱进行求解。双目标消防救援站选址模型仍采用CYYPO算法进行求解,参数设置保持不变。考虑从50个备选点选择3个、4个和5个待建点三种情况。
在第一种选址问题中,最大覆盖模型和双目标选址模型的选址方案各为(28,40,50)和(20,24,32);综合覆盖水平各为409.4058和575.1102;总成本各为548和469。在第二种选址问题中,这两种模型的选址方案各为(8,26,40,48)和(13,34,38,41);综合覆盖水平各为422.9375和579.9749;总成本各为769和622。在第三种选址问题中,这两种模型的选址方案各为(5,34,45,49,50)和(8,15,33,35,46);综合覆盖水平各为405.7096和584.4218;总成本各为1076和962。从上述结果可以发现,和最大覆盖模型相比,双目标选址模型不仅可以提高总救援服务质量,而且可以降低总建设成本。
此外,还比较了这两种模型有关四种风险等级需求点的时效性指标。在第一种选址问题中,对最大覆盖模型而言,风险等级为极高、严重、中等和轻微的需求点时效性平均值各为0.7491、0.6742、0.5122和0.5869;时效性值为1的比例各为50%、38%、8%和14%。对双目标选址模型而言,这四种需求点时效性平均值各为1、0.9362、0.8856和0.8349;时效性值为1的比例各为100%、69%、62%和63%。
在第二种选址问题中,对最大覆盖模型而言,四种风险等级需求点时效性平均值各为0.8815、0.6382、0.5349和0.6408;时效性值为1的比例各为75%、15%、15%和32%。对双目标选址模型而言,这四种需求点时效性平均值各为1、0.9510、0.8642和0.8721;时效性值为1的比例各为100%、77%、69%和64%。
在第三种选址问题中,对最大覆盖模型而言,四种风险等级需求点时效性平均值各为0.6893、0.6283、0.5251和0.8223;时效性值为1的比例各为42%、31%、23%和59%。对双目标选址模型而言,这四种需求点时效性平均值各为1、1、0.8840和0.8303;时效性值为1的比例各为100%、100%、54%和50%。
从上述结果可以知道,在这三种选址问题中,在绝大多数时效性评价指标方面,双目标选址模型均明显优于最大覆盖模型。究其原因,所建模型在考虑消防救援水平总体最优情况下,也可以提高大多数类型需求点的平均救援水平。需要指出的是,采用其它非劣解和最大覆盖模型的计算结果进行比较时,也会得到类似结论。因此,本文为消防救援站布局规划提供了一种可行有效的选址模型。
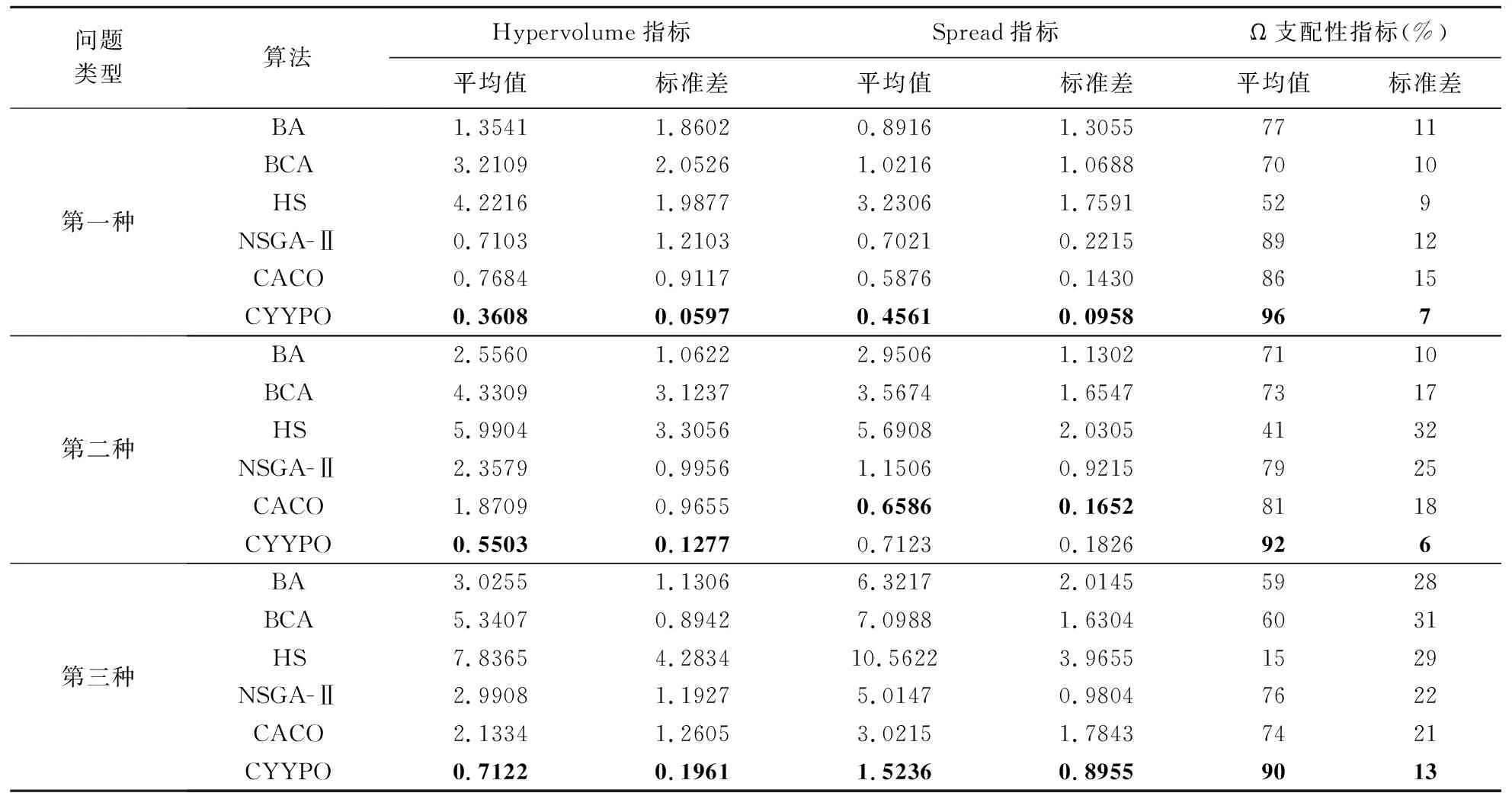
表1 六种多目标智能优化算法计算结果比较
4.3 不同算法的求解性能比较
为进一步测试CYYPO算法的计算性能,选择蝙蝠算法BA、蜂群算法BCA、和声搜索算法HS、NGSA-Ⅱ和元胞蚁群优化算法CACO进行对比测试。为公平起见,这6种算法设置相同最大函数评价次数,均为40000次。CYYPO算法参数设置保持不变,其它算法参数根据文献[8]和[10]进行设置。
采用常用的Hypervolume指标[8,12]、Spread指标[8,12]以及Ω支配性指标[8,12]进行算法优化性能比较。第一个指标用于评估算法非劣解集收敛性。该指标值越小,说明算法非劣解集收敛性越好。第二个指标用于评估非劣解集的多样性与分布均匀性。该指标值越小,算法非劣解集的多样性越好,分布更加均匀。第三个指标用于评估算法获得优秀结果比例。该指标越大,说明算法得到非劣解数量越多。
在实验中,仍然考虑上述三种选址问题。针对每一种问题,这6种算法各自运行30次,分别统计上述三种指标的平均值和标准差。实验结果如表1所示。此外,由于所求解问题真实Pareto最优解集未知,本文先求出所有算法得到的非劣解集的并集,再取其中的非支配解集作为近似Pareto最优解集。
从表1可以发现,对于Hypervolume指标、Spread指标和Ω支配性指标而言, CYYPO算法在绝大多数选址测试问题上优势显著。在迭代过程中,CYYPO算法充分利用阴阳平衡优化算法全局探索能力强的特点,即利用P2在超球体内进行全局搜索,以搜索到尽可能多的含有Pareto最优解区域;在算法搜索空间寻优的个体同时也分布在元胞空间,利用演化规则在邻居范围内对这些区域进行精细化搜索。此外,通过P1和P2的互换策略实现优化信息在算法搜索空间和元胞空间共享,寻优个体可以动态调整搜索行为。随着优化搜索的深入,CYYPO算法能够向分布在不同区域的多个Pareto最优解逼近。因此,新算法的非劣解集的收敛性、分布的多样性和均匀性更好。
此外,还测试了这6种算法优化速度,比较这些算法获得指定非劣解个数(分别为4、6和8)的平均计算时间。在第一组问题中,这6种算法平均计算时间各为7.2、9.8、12.3、6.1、5.6和2.5。在第二组问题中,这6种算法平均计算时间各为19.6、18.7、27.6、11.3、13.4和3.4。在第三种问题中,除HS没有在30分钟内获得指定数量的非劣解外,其它5种算法平均计算时间各为28.5、27.1、22.3、24.9和6.7(单位:分钟)。在所有测试问题上,CYYPO算法所需要的平均计算时间都是最少的。因此,本文为双目标消防救援站选址问题的求解提供了一种有竞争力方法。
5 结束语
消防救援站选址是应急管理中一类重要研究问题。本文引入时效性评价函数衡量救援服务质量,构建考虑时效性的综合覆盖水平以及总建设成本的双目标选址模型,并设计元胞阴阳平衡优化算法进行求解。实验表明,所建立的模型可以有效求解消防救援站布局规划问题。和5种智能优化算法相比较,所设计算法具有更好优化性能。在选址基础上,考虑消防车辆调度问题是下一步研究方向。
