如何帮助学生练就“数学的眼光”
2022-02-08王文英
○王文英
“会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界”是《义务教育数学课程标准(2022年版)》(以下简称《课标(2022年版)》)的课程目标。如何将“三会”素养落地是数学教学研究的主要内容,本文拟就培养“数学的眼光”谈谈自己的思考与实践。
一、如何理解“数学的眼光”
什么是“数学的眼光”?《课标(2022年版)》指出:数学为人们提供了一种认识与探究现实世界的观察方式。简而言之,“数学的眼光”就是数学的观察方式。观察是有目的、有计划的知觉活动,是以视觉为主,包含着积极的思维活动,融其他感觉为一体的综合感知。史宁中教授认为,学过数学的人看世界会抽象,会一般地看问题,数学的眼光最主要表现为抽象。
抽象是从许多事物中舍弃个别的、非本质属性,得到共同的、本质属性的思维过程,是形成概念的必要手段。《课标(2022年版)》指出,数学中的抽象主要是指对现实世界中数量关系与空间形式的抽象,通过抽象得到数学的研究对象,形成数学概念、性质、法则和方法。因此,练就“数学的眼光”应着力培养学生的数学抽象能力。
数学抽象主要包括两个方面:数量与数量关系、图形与图形关系。这就意味着,数学抽象不仅仅要抽象出数学所要研究的对象,还要抽象出这些研究对象之间的关系。数学抽象可以理解为过程,即如何将数学的研究对象从现实世界的情境中层层剥离,抽象出数学的研究对象及其关系的过程。如通过观察斜拉桥的钢索、人字梁、自行车三脚架,忽略其颜色、材料质地等,将其外形画下,则都是三角形。再进一步观察,发现都是三角形但大小不同,其大小与底和高的长短有关。这一系列的过程是抽象。
数学抽象还可以理解为结果,即如何用形式化的语言表征数学对象及事物之间简单的联系与规律。如天平保持平衡,通过观察,用3x=150 这个数学的式子表示相等关系,这也是抽象。
数学教学的过程应该是帮助学生不断进行数学抽象的过程,在抽象的过程中,让学生认识所学的数学知识,了解知识间的联系,发现事物之间的规律,并且养成从数学的角度观察现实世界的意识和习惯。如果学生拥有这样的意识和能力,那就具有“数学的眼光”。
二、如何练就“数学的眼光”
1.培养数学观察的意识。
让学生养成从数学角度观察现实世界的意识与习惯,是练就“数学的眼光”的关键。
第一,让学生明确“观察什么”。数学观察不同于语文、美术等学科,主要聚焦的是数量和数量关系、图形和图形关系。从一年级起,教师要有意识地加以引导。比如一年级上册教材,一开始就安排了“数一数”“比一比”“分一分”“认位置”四个内容。通过教学,不仅要让学生学会怎么数、怎么比、怎么分、怎么描述位置,更重要的是让学生知道,“数”“比”“分”以及“位置”都是数学研究的内容,可以从“数量有多少”“数量之间有什么关系”“怎样确定标准去分类”“如何描述物体的位置”这些角度去观察现实世界的客观现象,这些角度既是数学观察的角度,得到的也是数学的信息。同时,随着年级的升高,需让学生掌握数学观察的其他角度,了解哪些信息是属于数学的信息。
第二,让学生知道“怎么观察”。如何观察,包含两个方面。一是从哪里着眼。一般来说,是先整体后局部。无论是主题图还是现实情境,整体观察,初步了解其中包含的数学信息,然后局部观察,具体观察相应的对象。二是观察时做什么。观察不仅仅是看,还需要想,需要写。要让学生养成边观察边思考、边观察边记录的习惯,及时将看到的与已学的知识联系起来,将看到的与想到的记录下来。
如这道题(图1):涂色部分的面积比空白部分的面积大16平方厘米,空白部分的面积是多少?
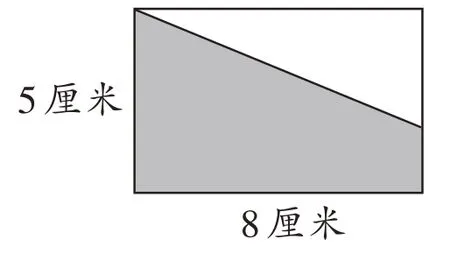
图1
从常规角度思考,要求空白部分面积需将长方形面积减去涂色部分的梯形面积,显然,这里的梯形面积很难求出。然而,一个学生在观察时,将题意用线段图表示出来(图2),就将问题化为相对简单的和差问题,用(40-16)÷2 就使问题得以解决。
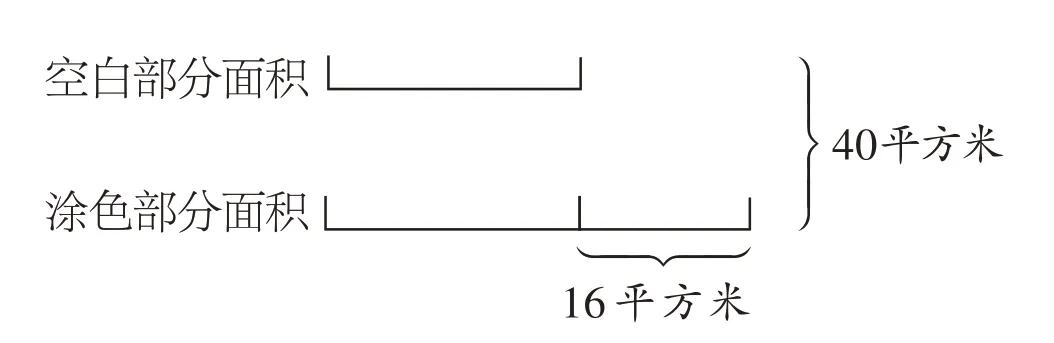
图2
第三,需要不断促使学生观察进阶。从一开始观察数量的多少到关注数量之间的关系,从知道图形是什么到清楚图形之间的关系,教师需要根据学生对知识掌握的情况对观察的视角与内容作更高的要求。如在认识乘法后,要求学生从“几个几”的角度去观察并描述;在认识数级后,引导学生看到大数目就会自动分级,分析亿级、万级和个级上的数分别是多少。从模糊的整体到清晰的局部,再到相对精准的整体,说明学生观察的视角和能力在不断进阶。
2.教会数学抽象的方法。
会观察是前提,将观察的结果用形式化的方式表示出来,就实现了数学抽象,这是练就“数学的眼光”的重要体现。
第一,引导比较。抽象需要引导学生抽取事物的本质特征,舍弃其非本质特征。需要教师有意识地引导学生对不同事物进行比较。如教学《认识圆柱体》,教师可以出示生活中的一些圆柱形的物体,如茶叶罐、蚊香盒、铅笔等,引导学生观察并思考:这些物体的形状是什么?它们都是不同的物体,为何都称之为圆柱?这些问题驱使学生发现不同圆柱物体的本质特征,即“上下一样粗”“上下是圆形,大小相等,中间是个曲面”。当学生发现其相同点之后,教师继续追问:“它们都是圆柱体,有不同之处吗?”学生不难发现,同是圆柱,但因高矮、胖瘦不同,其大小不同。透过现象看到本质,这是抽象的关键一步,显然,通过比较能够达成。
第二,适当表征。当学生成功抽取事物的本质属性之后,教师要鼓励学生用形式化的方式将之表示出来。如上例,教师可以这样小结并提问:“尽管这些圆柱粗细、高矮各不相同,但它们有本质的相同之处,能否尝试画出一个圆柱表示它们的相同之处呢?”史宁中教授认为,几何抽象的本质就是把三维的物体用二维图形表现出来。让学生将自己观察发现的结果在纸上画出来,画的过程实际就是将圆柱形物体抽象成圆柱形的过程。
第三,赋予意义。当抽取出圆柱形之后,教师还需要带着学生向前一步,即给出不同大小的圆柱形,让学生想象可能表示生活中的哪个物体。根据图形想物体,这一逆向的观察思考对培养学生的空间观念非常有益。教学中,很多教师容易忽略这一环节,往往表征后被认为完成了抽象,殊不知,当抽象之后赋予其现实意义,这样的抽象才更完整。
3.创造应用数学的机会。
数学与生活是密切联系的,引导学生在日常生活及其他学科中发现并研究数学问题,是练就“数学的眼光”的重要途径。
可以把生活情境引入数学课堂。首先,将生活情境引入课堂发现数学问题。如一位教师创设了这样的情境:茫茫大海上,一艘轮船出了事故,需要紧急救援。作为搜救艇艇长,了解哪些信息后才能施救?学生不难发现,艇长必须准确地了解轮船的位置,即“在什么方向,距离多少”。其次,将生活情境引入课堂帮助理解数学知识。“半个月前,妈妈买了一箱苹果共20 个,第一个星期全家人吃了6 个,第二个星期全家人吃了8 个,现在还剩多少个?”用这个生活实例帮助学生理解减法的性质。再次,还可用生活情境检验学生知识掌握的情况。如教学《认识圆》后,教师设计问题:妈妈准备过年全家聚餐,是选择用条形桌、八仙桌还是圆桌?请说明理由。以此来检验学生对圆的特征的掌握程度。
以主题学习探究现实世界。在教学中,教师可以通过组织主题学习,给学生提供应用数学知识探究现实世界的机会。如将常见树叶的形状、周长、面积,以及包含的“比”等知识作为学习内容,让学生体会数学学习的价值,探究树叶这一常见事物蕴含的数学信息,激发对现实世界的好奇心和对数学学习的求知欲。
三、练就“数学的眼光”几个注意点
1.“三会”素养是一个整体。
“数学的眼光”“数学的思维”“数学的语言”作为“三会”的具体内容,《课标(2022年版)》对它们分别作了阐述,并有具体要求。作为教师,需要明确的是,它们是一个整体,尽管在培养过程中有所侧重,但非独立存在。如《认识乘法分配律》的教学,教师设计了三个环节:第一,引导学生观察不同情境:鼓乐队添服装、两辆车从两地相对驶出相遇求路程、两块长方形地求总面积。学生发现求解三个问题都可以用两种方法解决,一种是先相加再相乘,另一种是分别乘再相加。第二,在此基础上引导学生猜想、验证,发现规律,并用含有字母的式子表示,即(a+b)c=ac+bc。第三,应用规律解决实际问题。在这个过程中,“三会”的培养都有具体落实。
2.培养“数学的眼光”有阶段性。
在课堂教学中,培养“数学的眼光”并非一蹴而就,需要日积月累,逐步递进。如《用字母表示数》,教材安排在五年级教学,但这并不意味着五年级才开始培养学生的符号意识。符号意识的培养从一年级起就应该渗透。比如,白兔和黑兔一共有15 只,其中白兔有8 只,黑兔有多少只?可以鼓励学生用□表示黑兔,用8+□=15 来表示这道题。随着□表示未知数→用字母表示未知数→字母不仅表示未知数,还可以表示变化的数,学生逐渐使用符号→体会字母表示数的意义→自觉地用字母表示数。因此,同样是符号意识的培养,不同学段应该有不同的要求。
