制动条件下高速列车轮轨动态响应特性分析

MICHEALE YIHDEGO GEBREYOHANES,莫继良,楚 明,张 亮,王志伟

(西南交通大学 机械工程学院， 成都 610031)

0 引言

制动是通过制动盘与制动闸片相互作用产生摩擦力矩并传递至轮轨界面形成阻碍列车前进的制动力而实现的[1-2]。因此，列车制动对轮轨相互作用具有重要影响[3]。随着列车运营速度的不断提高，制动条件下轮轨间的动态响应也越来越复杂[4]。当轮轨相互作用通过轴箱、悬挂系统传递至转向架及车体时，将进一步影响车辆系统的动力学行为，严重威胁车辆系统的稳定性和列车的安全运营[5]。因此，开展制动条件下高速列车轮轨动态响应分析并掌握其演变规律及行为特性具有重要意义[6]。

目前，国内外学者针对制动条件下轮轨动态特性开展了大量研究。李亨利等[7]运用多体动力学理论建立了车辆系统动力学模型，分析了坡道制动时车辆的动力学行为以及制动压力对轮轨接触关系和车轮磨耗特征的影响。Tran等[8]搭建了高速列车动力学模型并探究了紧急制动条件下制动力矩、轮轨接触状态及列车运营速度对轮轨力及车辆系统动态响应的影响。马卫华等[9]通过数值模拟分析了机车在惰行和制动过程中不同类型的轮径差与轮轨相互作用的关系。杨亮亮等[10]建立了重载列车动力学模型，分析了制动条件下列车通过曲线时车轮的磨耗分布特征及轮轨滚动阻力特性。孙树磊等[11]探究了紧急制动工况下车辆通过曲线时的轮轨横向力和脱轨系数。以上研究成果对认识制动条件下轮轨相互作用具有重要意义。然而，目前针对高速列车制动条件下轮轨动态特性的数值分析大都忽略了轨道柔性变形的影响，仿真结果不能准确地反映轮轨系统及车辆系统在实际服役过程中的动力学行为。周新建等[12]建立了考虑轨道柔性的高速列车动力学模型，分析了柔性轨道条件下轮轨接触振动特性和蠕滑力。王相平等[13]分析了柔性轨道结构上车辆系统动力学性能的变化情况，结果表明考虑柔性轨道能够更准确地反映高速列车车辆系统的动态响应。相关研究说明了轨道柔性变形对车辆-轨道系统动力学行为及轮轨间作用力具有重要影响。因此，为准确评估车辆-轨道系统动态特性，保障列车服役安全，亟需开展制动条件下考虑轨道柔性变形的高速列车振动特性及轮轨动态响应研究。

首先建立了柔性轨道的有限元模型，并进一步利用多体动力学软件Simpack搭建了车辆-轨道空间耦合动力学模型，通过轮轨关系实现了柔性轨道系统和多刚体车辆系统的动态耦合。然后，通过线路实验验证了模型的正确性。最后，基于建立的模型，分析了制动条件下轨道柔性变形对高速列车轮轨间作用力和轴箱振动响应的影响，探究了不同速度等级、不同制动力矩下高速列车轮轨动态行为的演变规律，揭示了制动条件下造成轮轨力差异的原因。

1 车辆-轨道空间耦合动力学模型

1.1 车辆系统动力学模型

基于高速列车结构参数及工作原理，建立多刚体车辆系统动力学模型，其拓扑图如图1所示。该模型由1个车体、2个构架、4个轮对、3个制动盘以及8个轴箱组成。车体与构架通过二系悬挂系统连接，构架与轴箱通过一系悬挂连接。其中，通过阻尼弹簧单元模拟悬挂系统，其动态相互作用力是利用部件之间的相对位移和速度计算的。车辆系统具体建模参数与文献[14]保持一致。

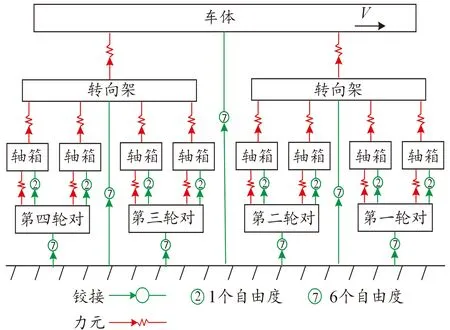
图1 车辆系统动力学模型拓扑图

建立的车辆系统动力学模型中每个部件最多考虑6个自由度，分别是纵向、横向、垂向、侧倾、俯仰和横摆运动。基于各部件在车辆系统中的运动情况，可以将整个车辆系统简化成包含50个自由度的多刚体动力学模型。基于牛顿第二定律，系统的二阶振动微分方程可以表示为：

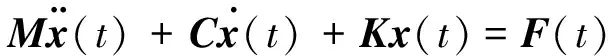
(1)

式中：M为系统质量矩阵；C为系统阻尼矩阵；K为系统刚度矩阵；x(t)为系统各自由度的位移向量；F(t)为广义力向量。

1.2 柔性钢轨动力学模型

1.2.1钢轨与轨道板有限元模型

为了更加准确地反映制动过程中轮轨动态作用，建立考虑钢轨及轨道板柔性变形的轨道系统动力学模型。首先，基于钢轨和轨道板几何结构参数，建立钢轨和轨道板三维实体模型。然后，基于三维实体模型建立钢轨和轨道板有限元模型，如图2所示。钢轨采用60轨，每一单元长度为1.2 m，轨面廓形为CN60，尺寸为6.6 m×2.55 m×0.3 m。

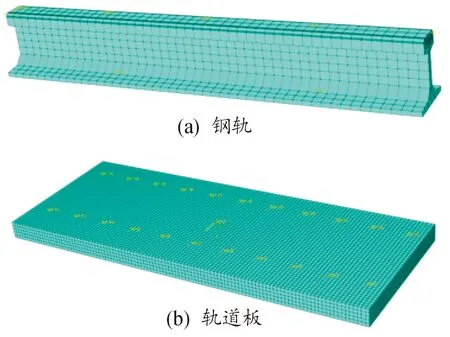
图2 钢轨和轨道板有限元模型示意图

1.2.2子结构分析

对于许多大型复杂的结构，如何在提高计算效率的同时保证计算精度是有限元法进行动态计算面临的重要难题。鉴于此，用近似的和简单的减缩模型代替原模型的自由度减缩技术，得到了广泛的发展和应用。Guyan法是一种常用的自由度减缩方法，广泛应用于车辆-轨道系统的刚柔耦合动力学建模，对于无阻尼系统，根据需要把模型的自由度分为主自由度和从自由度，对质量矩阵和刚度矩阵进行主自由度提前并分块，假设在从自由度上无外力作用，系统的运动方程可以表示为下式：

(2)

式中m和s分别表示系统的主自由度和从自由度。由式(2)的第二列可得：

(3)

不考虑从自由度上惯性的影响，式(3)可写为：

Ksmxm+Kssxs=0

(4)

然后可得：

(5)

式中TG为坐标转换矩阵。将式(5)代入式(2)可得到减缩模型：

(6)

1.2.3柔性轨道系统的建立

采用减缩的钢轨和轨道板模型，并采用模态叠加法，钢轨和轨道板的控制方程可用常微分方程表示，则柔性轨道模型的振动方程如下：

(7)

式中：MT为轨道系统质量矩阵；CT为阻尼矩阵；KT为刚度矩阵；XT表示系统各自由度的位移向量；FWR为轮轨界面的非线性接触力。

有限元模型中，钢轨的密度为7 850 kg/m3,弹性模量为210 GPa,泊松比为0.3；轨道板的密度为2 500 kg/m3,弹性模量为39 GPa,泊松比为0.3。这里列出钢轨和轨道板前几阶典型的模态，如图3所示。

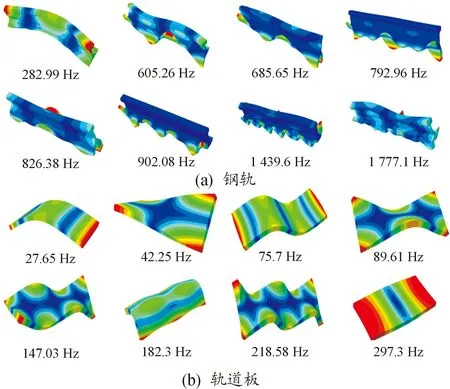
图3 钢轨和轨道板前几阶典型模态示意图

1.3 耦合动力学模型

轮轨关系是连接车辆与轨道系统之间的桥梁，主要包括2个基本问题：轮轨几何接触关系和轮轨接触力。其中，轮轨接触力主要包括法向接触力和切向蠕滑力。基于非线性赫兹弹性接触理论，轮轨法向接触力表示如下：

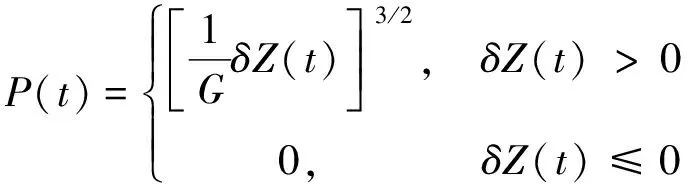
(8)

式中：P(t)为法向轮轨力；G为轮轨赫兹接触常数；δZ(t)为轮轨接触面法向弹性压缩变形。基于法向接触力的基础上，采用Kalker线性蠕滑理论[15]计算了轮轨切向蠕滑力并用Shen-Hedrick-Elkins模型[16]进行修正。

至此，完成车辆-轨道空间耦合动力学模型的建立，如图4所示。

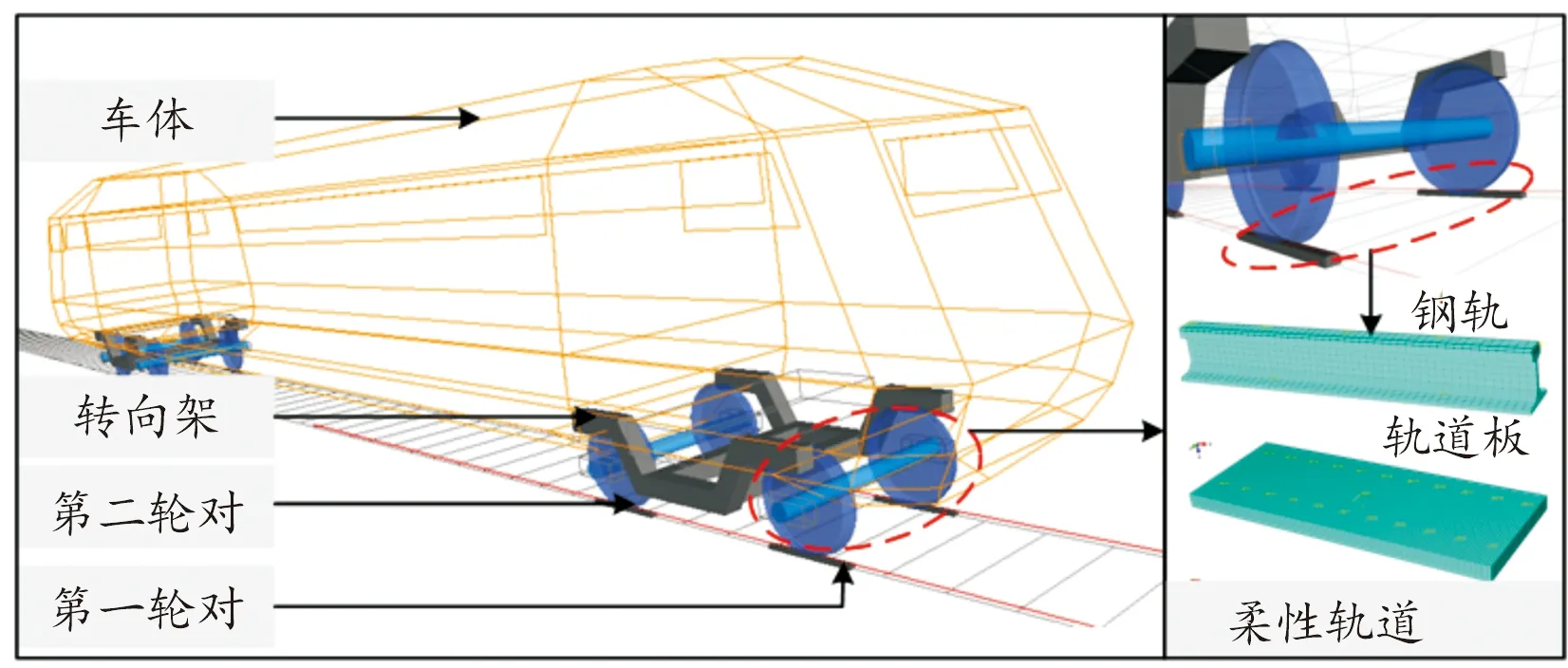
图4 车辆系统动力学模型示意图

2 动力学模型的验证

为验证刚柔耦合动力学模型的正确性，开展了动车组线路试验。试验过程中，车辆以300 km/h速度运行，转向架及轴箱上加速度传感器具体位置如图5所示，同步采集构架与轴箱振动加速度信号，采样频率为5 000 Hz。另外，基于建立的车辆系统动力学模型，开展了仿真分析，其仿真工况与现场试验保持一致。

图5 构架及轴箱上加速度传感器具体位置示意图

图6(a)和图7(a)分别为通过现场试验和仿真获取的构架和轴箱上振动加速度的时域结果。可以看出，试验得到的振动加速度均略大于仿真的结果。通过试验和仿真获取的构架上振动加速度均方根值分别为0.29g和0.27g，误差为6.9%。试验和仿真获取轴箱上振动加速度的均方根值分别为1.9g和2.2g，相差13.6%。图6(b)和图7(b)分别为构架和轴箱振动加速度信号对应的频域结果。结果表明，试验与仿真条件下构架和轴箱的频谱结果均有30 Hz的主频。此外，构架频谱图还出现了10 Hz的主频，与转向架构架的沉浮频率吻合。结果表明，仿真和线路试验结果存在一定的误差，这是由于建模过程中忽略了复杂的线路条件以及关键零部件的柔性变形所致。总的来说，建立的动力学模型基本上能够反映实际服役过程中车辆系统的振动特性，验证了模型的有效性。

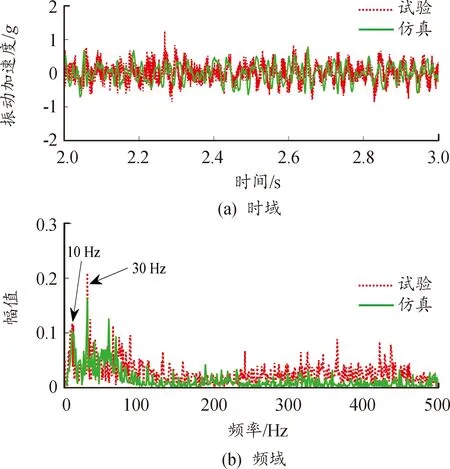
图6 试验与仿真获取的构架振动加速度

图7 试验与仿真获取的轴箱振动加速

3 仿真分析与讨论

3.1 钢轨柔性变形对轮轨力影响分析

为了探究钢轨柔性变形对轮轨作用的影响，分别基于刚性和柔性轨道的动力学模型进行仿真计算与结果分析。图8为300 km/h速度等级下高速列车分别在刚性和柔性轨道上以24 kN·m的制动力矩实施紧急制动时，第一轮对轮轨垂向力的时间历程曲线。在刚性轨道上制动时，第一轮对的轮轨垂向接触力最大值为90.82 kN。考虑轨道柔性后，轮轨垂向接触力大幅增加，最大轮轨垂向接触力为124.22 kN (增加了36.8% )，且幅值变化更为显著。结果表明柔性轨道对轮轨垂向接触力影响显著。

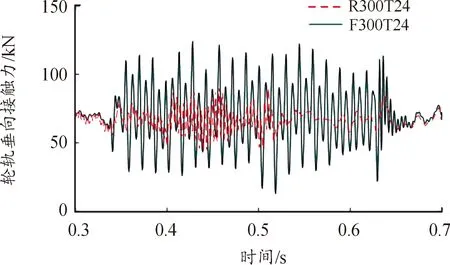
图8 第一轮对轮轨垂向接触力曲线

同样地，对第二轮对的轮轨垂向接触力进行时域分析，结果如图9所示。

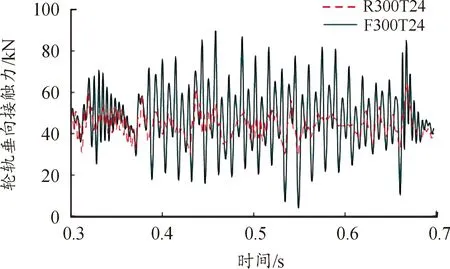
图9 第二轮对轮轨垂向接触力曲线

列车在刚性轨道上制动时，轮轨垂向接触力的最大值为80.56 kN，在柔性轨道上制动时，最大轮轨垂向接触力为89.78 kN，最大值增加了10.26%。此外，与第一轮对相比，第二轮对在刚性和柔性2种不同轨道上的轮轨垂向接触力差异更小。这是制动过程中车辆点头运动造成的。同样，第三、第四轮对在柔性轨道上制动时的轮轨垂向接触力与在刚性轨道上相比显著增加。结果表明在高速列车仿真分析中应充分考虑轨道柔性，以便准确反映车辆运行过程中的动态响应。

轮轨纵向蠕滑力是反映轮轨间作用力的重要指标。为此，进一步分析列车制动时第一轮对分别与刚性和柔性轨道接触产生的纵向蠕滑力，相应的时间历程如图10所示。对于刚性轨道，轮轨纵向蠕滑力的最大值为35.20 kN，而对于柔性轨道，轮轨纵向蠕滑力的最大值为45.66 kN，即考虑轨道柔性变形后最大蠕滑力增加了22.90%。第二、三、四轮对与轨道间的纵向蠕滑力也可观察到相同的现象。

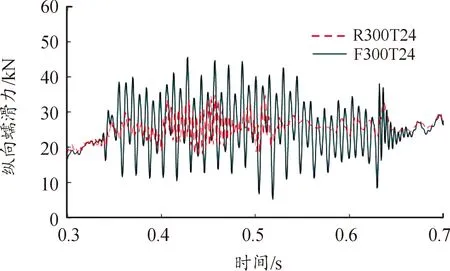
图10 第一轮对的纵向蠕滑力时间历程曲线

轴箱是连接轮对与转向架的重要部件，轮轨相互作用力、振动或激励均可通过轴箱传递至转向架，进而影响车辆系统的动力学行为。图11为刚性和柔性轨道作用下轴箱的垂向振动加速度曲线。

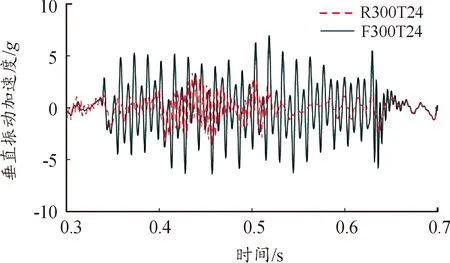
图11 轴箱的垂向振动加速度曲线

可以发现，考虑轨道柔性后轴箱垂向振动加速度的最大值从3.49g增加到6.99g，且振荡幅值显著增大。结合轮轨间作用力分析结果，可以推测，在轨道柔性作用下，轮轨垂向接触力和纵向蠕滑力的最大值和变化幅值均增大，导致轴箱振动加剧，进而影响车辆系统的稳定性。因此，在车辆系统动力学仿真分析中，应充分考虑轨道的柔性变形，以更加准确地反映轮轨间的动态特性及车辆系统的振动响应。

3.2 不同制动工况下车辆轮轨力对比分析

制动工况是影响车辆系统动态响应的重要因素。采用考虑轨道柔性的车辆-轨道空间耦合动力学模型，结合刚性和柔性轨道上制动时列车动态响应的演变规律，本小节进一步研究不同制动工况对轮轨间相互作用力及轴箱振动响应的影响，并重点对第一、第二轮对的动态响应特性进行了探讨。设定高速列车行驶速度为300 km/h，图12为不同制动力矩下第一轮对的轮轨垂向力曲线。

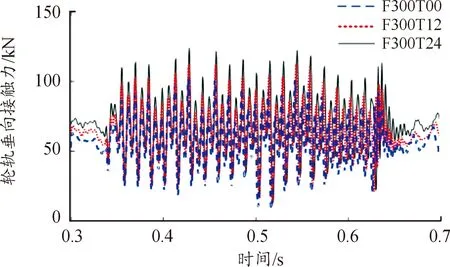
图12 不同制动力矩下第一轮对的轮轨垂向力曲线

随着制动力矩的增加，轮轨垂向接触力也显著增大，0、12、24 kN·m制动力矩对应的轮轨垂向接触力最大值分别为102.14、112.91和124.22 kN。图13的结果表明不同制动力矩下第二轮对轮轨垂向接触力的变化趋势与第一轮对相反，即轮轨垂向接触力随制动力矩的增大而减小，0、12和24 kN·m制动力矩对应的轮轨垂向接触力最大值分别为 104.9、97.73和89.8 kN。因此，制动力矩增大将加剧转向架及车体的点头运动，从而导致制动过程中第一轮对与轨道的垂向接触力增加而第二轮对的轮轨垂向接触力减小。

图14为不同制动力矩下时速300 km/h高速列车轴箱振动加速度的时域响应曲线。当车辆未施加制动力矩时，轴箱垂向振动加速度的最大值为5.96g。当分别采用12、24 kN·m的制动力矩制动时，对应的轴箱垂向加速度最大值为6.24g和6.99g。结果说明制动力矩同样对轴箱的振动响应具有重要影响。

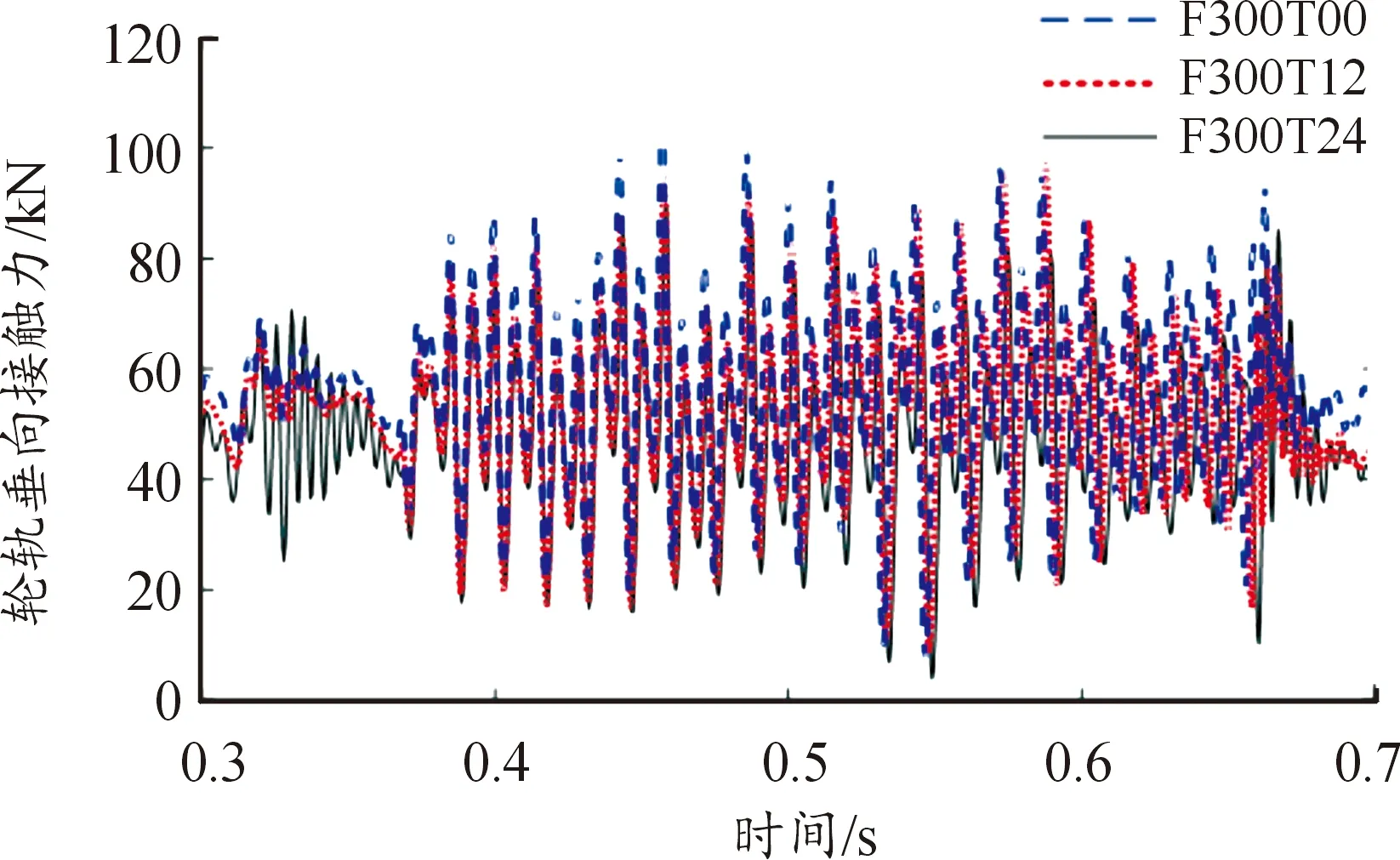
图13 不同制动力矩下第二轮对的轮轨垂向接触力曲线

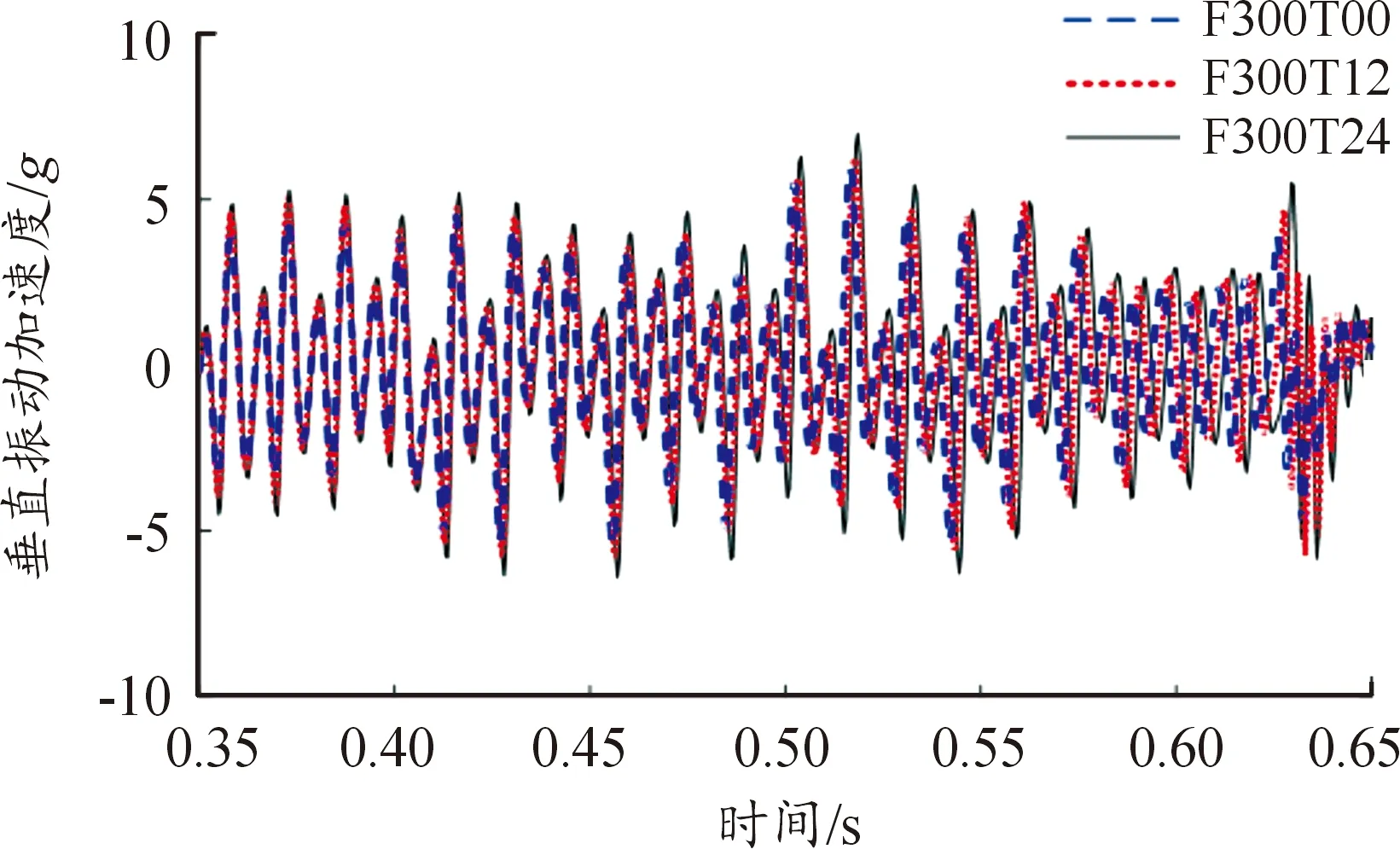
图14 不同制动力矩下轴箱的垂向振动加速度曲线

进一步，分析不同速度等级和制动力矩下轮轨的垂向接触力、纵向蠕滑力和磨耗系数。不同制动工况与运行速度下，第一轮对与第二轮对的轮轨垂向力的最大值计算结果如图15所示。

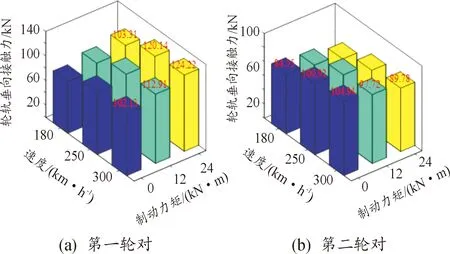
图15 不同制动工况下轮轨垂向接触力的最大值直方图

结果表明随着速度等级的增加，第一、二轮对的最大轮轨垂向力均增大。当运行速度为300 km/h时，相比于匀速运行，制动力为24 kN对应的第一轮对的轮轨垂向力增加了21.6%，第二轮对的轮轨垂向力减小了16.7%。图16为不同制动工况下车轮磨耗系数和轮轨纵向蠕滑力的均方根值直方图。结果表明，轮轨纵向蠕滑力和车轮磨耗系数均随着速度等级的增加而逐渐增大。此外，当制动力矩增大时，轮轨纵向蠕滑力和车轮磨耗系数急剧增加。因此，相比轮轨垂向接触力，制动力矩对轮轨纵向蠕滑力和车轮磨耗系数的影响更为显著。

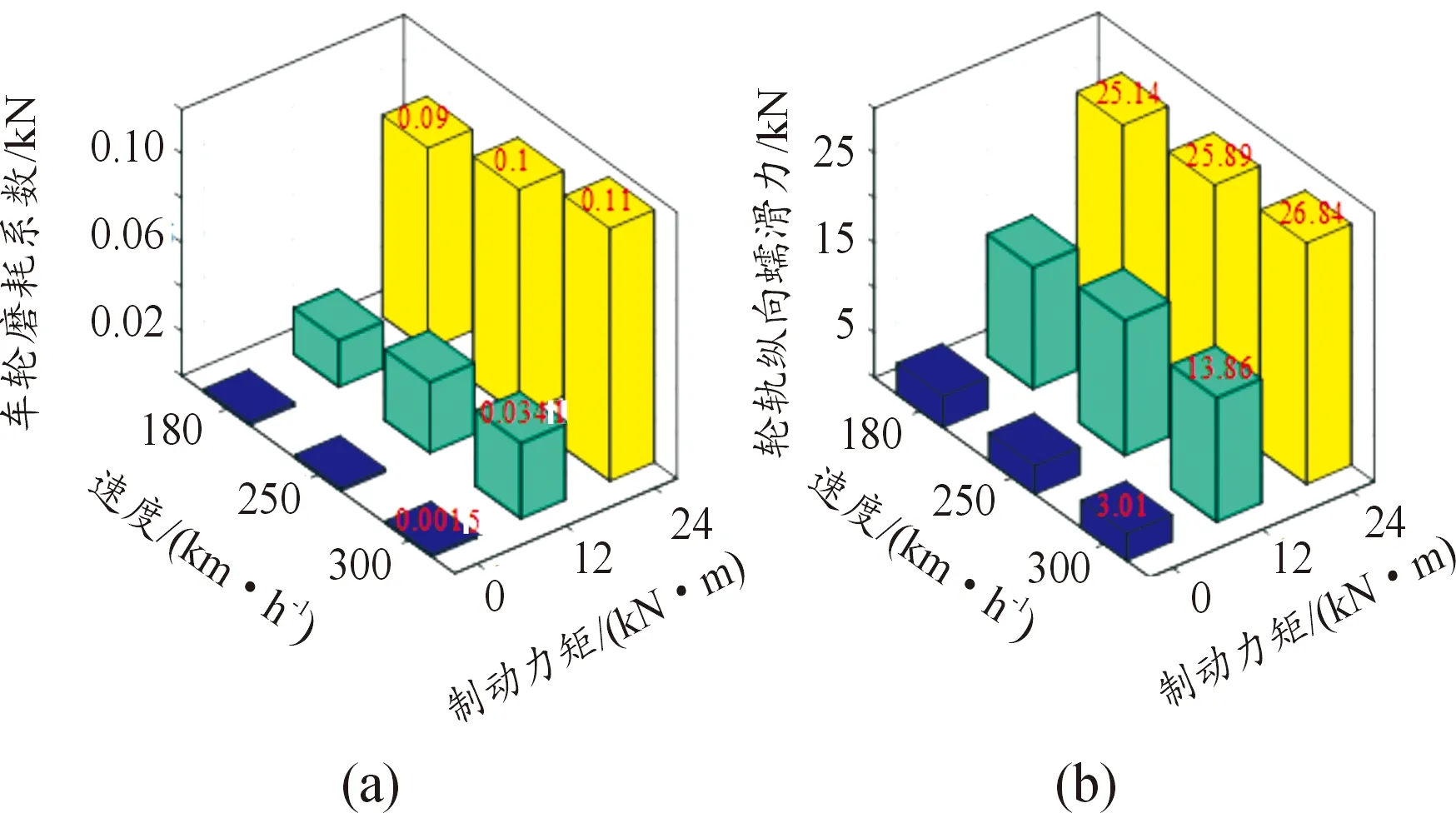
图16 不同制动工况下车轮磨耗系数和轮轨纵向蠕滑力的均方根值直方图

4 结论

基于有限元方法和多体动力学理论，建立了车辆-轨道空间耦合动力学模型，考虑了车体、构架、轮轨、轴箱等车辆系统关键部件的6个自由度，且考虑了的钢轨柔性变形，并通过轮轨垂向与切向作用关系，实现了车辆与轨道系统的动态耦合。通过对比仿真模拟与线路试验结果，验证了模型的有效性。基于此，分析了柔性轨道和制动工况对轮轨作用及轴箱振动的影响，主要结论如下：

1) 与刚性轨道相比，高速列车在柔性轨道上运行时轮轨垂向接触力和纵向蠕滑力的最大值和变化幅值均明显增加，轴箱振动加剧。因此，考虑轨道柔性变形后可更准确地揭示车辆系统的动态响应。

2) 随着制动力矩的增大，由于转向架和车体的点头运动加剧，第一轮对的垂向接触力增加而第二轮对的垂向接触力减小。当车辆制动初始速度等级增加时，第一、二轮对的垂向接触力均增大。

3) 列车在大的制动力矩或高的速度等级下制动均会增大轮轨纵向蠕滑力和车轮磨耗系数。并且，相比轮轨垂向接触力，制动力矩对轮轨纵向蠕滑力和车轮磨耗系数的影响更为显著。