Q学习实现亚马逊棋评估函数自调参

邱虹坤,王浩宇,王亚杰

(1.沈阳航空航天大学 计算机学院, 沈阳 110136； 2.沈阳航空航天大学 工程训练中心, 沈阳 110136)

0 引言

计算机博弈是人工智能领域的重要研究方向之一。近年来，计算机博弈的快速发展引起了国内外专家学者的高度关注。亚马逊棋正是一种新兴的计算机博弈棋种，它是一种两人完全信息动态博弈游戏。棋子的移动方式类似于国际象棋中皇后的走法，同时具有很强的领土控制特色[1-3]。

评估函数是亚马逊棋博弈程序中最为核心的部分之一，其作用是评估当前棋局局面的优劣性并为其打分。该分数作为后续博弈树搜索等一系列操作的基础，评估函数是否合理将直接影响到整个程序的棋力。对于亚马逊棋评估函数中的一些关键参数，目前主要通过人工方法，根据经验反复进行实验调参后才能确定，这种方法效率较低且精确度无法保证。一些学者的研究表明，通过引入强化学习的方式，可在一定程度上提高调参的效率和精确性[4-5]。

本文采用强化学习中Q学习的思路，设计了一种能实现评估函数自主调参的网络模型。相较于传统调参方法，该模型节省了大量的人力与时间，并且通过自主训练，对参数的调节也更加精确合理。

1 强化学习和Q学习

1.1 强化学习

在监督学习方式中，数据集的精确性很大程度上决定了训练结果的优劣性。然而在某些情况下，要生成大量准确合理的教师数据是十分困难的，如对棋盘博弈游戏或电子游戏的训练等。相比之下，强化学习更能胜任这些工作。强化学习是指在一连串行动的最后进行评价的学习方式。它不依赖于海量数据集的指导，而是通过不断与环境交互，总结经验并对行为的好坏进行评价打分，基于这些评价来推进学习[6-8]。该评价值被称之为奖赏(reward)。当强化学习到达某结果并获得奖赏时，与之关联的每一个行动都将被分配一定奖赏，以此来更新学习网络。

1.2 Q学习(Q-learning)

Q学习是最重要的强化学习算法之一，在该学习框架中，定义学习对象为Q值(Q-value)，代表选择下一个行动的指标数值集合，通常建立一个Q表格来存储。Q学习的最大特点在于将动态规划与蒙特卡洛方法结合，用于计算强化学习的整个马尔科夫奖励过程，得出最优策略[9-10]。其中马尔科夫过程又称马尔科夫链，指一系列不依赖于历史，仅根据当前来决定未来的状态集合，组成的无记忆的随机过程。而奖励过程则是在其基础上引入了奖励系数与衰减系数，因而可计算出某奖励链条上的收获(Return)[11]。

在训练初期，Q值被随机分配，此时相当于随机选择行动。在更新Q值时可以遵循以下规则：在行动获得奖赏时，增加与其相关行动的Q值；在没有获得奖赏时，利用与下一状态相关联行动的Q值来更新当前Q值[12]。如式(1)所示。

Q(St,at)=Q(St,at)+

α(r+γmaxQ(St+1,at+1)-Q(St,at))

(1)

其中：s、a分别代表t时刻的状态以及选择的行动，r、γ、α分别代表获得的奖励值、折扣率以及学习系数[13]。学习系数是用于调节学习速率的常数，一般取0.1左右；折扣率的引入用于避免产生状态的无限循环，一般取0.9左右[14]。

2 亚马逊棋评估函数设计

根据亚马逊棋的游戏规则，游戏一方的最终目的是用自己的棋子和障碍挡住对手的棋子，因此一般采取占领领土或阻塞对手路线的思路来设计评估功能[15]。亚马逊棋评估函数的设计主要是基于kingmove和Queenmove走法。Queen走法是按照国际象棋中的皇后走法，可以向横竖斜对角8个方向走直线，只要路径上没有障碍就可以沿直线一直走；king走法则是按照国际象棋中的国王走法，即只能向8个方向走一格。设t1、t2为territory特征值，代表双方对空闲区域的控制能力的评估值；c1、c2为位置position 特征值，用于反映双方对空格控制权的差值特征。a、b、c参数是根据棋局进行程度w而不断变换的权重，用于动态控制在不同棋局进度下各个特征值对结果的影响[16]。此外，为避免出现区域浪费情况(某空区域被围堵，不可再被使用)，定义参数S用于判断当前步法是否会产生该种区域的出现(称为缺陷区域)。需要注意，这里的“S”与式(1)中的“S”含义不同。式(1)中“S”代表强化学习模型中t时刻的状态；而这里的“S”是为避免出现区域浪费情况而在亚马逊棋评估函数中引入的参数。综上，可以得出评估函数的最终表达式，如式(2)所示。

Value=a×t1+b×t2/2+

c×((c1+c2)/2)+S

(2)

a、b、c3个权重系数的确定对最终估值精度有至关重要的作用。一个根据经验确定的权重与进度系数w的映射关系如式(3)所示[17]。其中，X值与Y值是决定评估准确性较为关键的参数，也是该评估函数中主要调参对象。

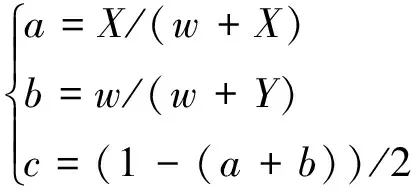
(3)

此外，虽然通过计算当前局面的领土特征值和棋子的灵活度等参数可以得到一个较为精确的评估价值，但有时仍会存在偏差，可以采用一种更为简单直观的方式来校准一下最终估值。通过“自对弈”的思路进行矫正，即以当前局面为基础，电脑控制双方随机走棋(在一个辅助棋盘中)，在合理时间内进行大量对局，从而计算出胜率。随机下棋虽然无规律性，但是模拟速度快。当进行大量模拟时也能一定程度上反映当前局面的优劣性。将模拟出的胜率与评估函数结果相结合即可达到调整效果。

3 Q学习调参模型

3.1 调参模型设计

本文主要的调参对象即为式(3)中的X值与Y值，可以采用迭代的思路实现自动调参，简单来说就是对X参数或Y参数分别进行增大或减小，。首先定义2个数值C1、C2，分别代表对X、Y进行加或减操作时的变化值。以X、Y的具体数值代表当前状态，而变更数值的方式则称为“行动”。因此，结合一般手动调参的方法，对于每种情况都有6种后续可能的行动，如表1所示。表中前4种行为对应的就是“增大X”“减小X”“增大Y”以及“减小Y”。而5、6号行动的引入分别对C2进行加操作以及对C1进行减操作，目的是避免发生多次行动后的参数恰好未发生变化，导致调参陷入死循环。对此，建立一个三层六叉树作为整体学习训练框架，共43个结点，如图1所示。

表1 后续行动方式

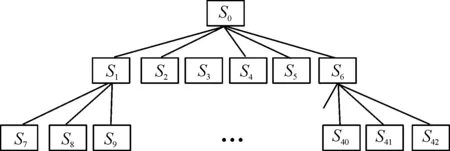
图1 三层训练网络结点关系图

模型利用对局的胜负情况来确定是否进行奖赏。首先记录下初始的参数值：X0、Y0，而后经过一系列行动选择后获得新的参数值：X1、Y1。将新旧参数带入博弈程序中调用，并进行数局对弈[18]。若新参数的胜率大于旧参数，则可以认为这是一种较好的调参策略，并对该行动路径上所有结点的Q值进行奖赏操作。之后再重新选择行动，获得新的X1、Y1并进行奖赏评估。反复执行此过程后，最终会得到一条较为稳定的，Q值相对较高的行动路线[19]。按照该行动路线更新评估函数参数，即代表完成了一次调参操作。之后初始化整个训练模型，以更新后的评估参数为基础，进行新一轮训练。如此反复以达到自调参的目的。整个训练流程如图2所示。

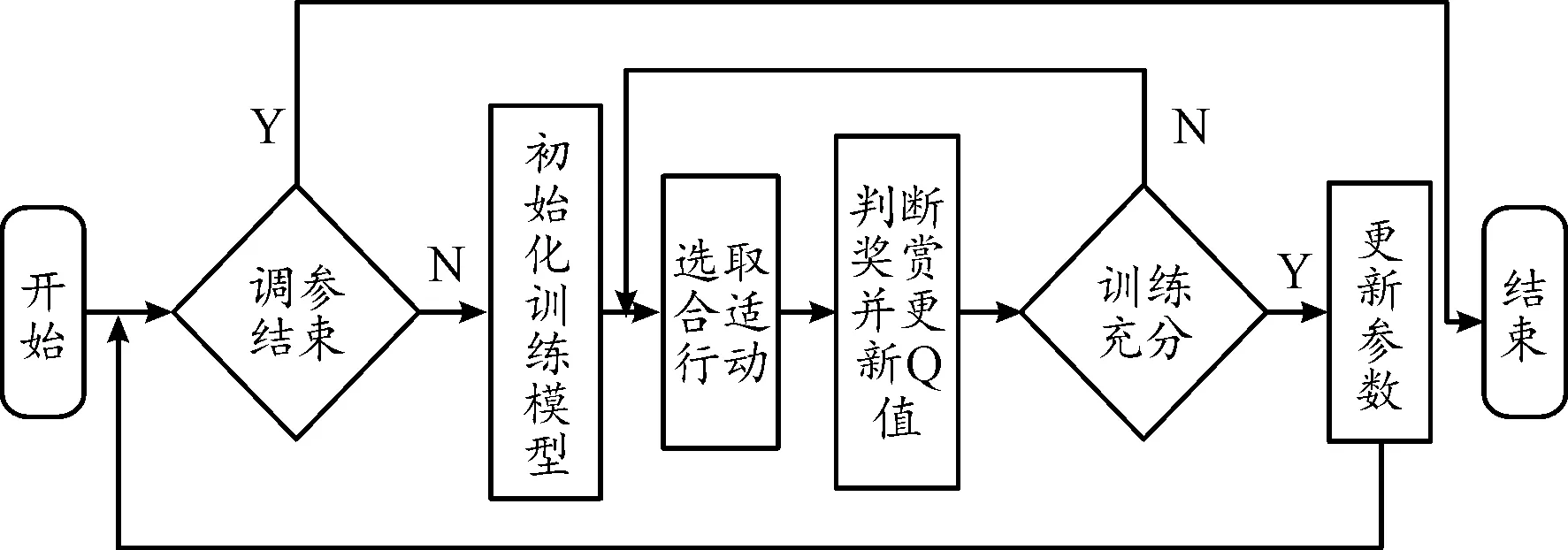
图2 训练流程框图

3.2 调参模型实现

调参模型是在博弈程序的基础上构造而成。首先定义节点型结构体node，内容包括每个结点的Q值，对X参数和Y参数所进行的操作，以及其6个孩子结点，可利用一个数组存储。定义全局变量Weight，用于存放参数值；定义一个整形数组path，用于存放选择过的行动路径。

程序主要包括3个功能函数：为模型初始化、行动判断、Q值更新。模型初始化时要求对所有结点信息进行初始化，包括Q值的随机分配、行动定义以及孩子结点的链接等。行动选择的基本思路是优先选择Q值最大的行动，但可能会出现某一高Q值行动被反复选择，同时其他行动无法得到训练的情况。该问题可以通过ε-贪心法(ε-greedy)的思路解决。首先确定一个ε值并生成一个0～1的随机数，若该随机数小于ε，则忽略Q值进行随机行动选择；若大于ε，则选取Qmax行动[20]。

Q值更新主要基于式(1)进行计算，将学习系数设为0.1，折扣率设为0.9。首先执行新旧参数的自对弈功能，通过对弈结果判断是否奖赏。如果能获得奖赏，则将奖赏按比例加到Q值上；若不能，则从下一状态所能选择的行动中对应的Q值，将最大值按比例加到Q值上。由于叶子结点后无其他行动可选择，因此对于模型第二层和第三层的Q值更新需要分别采取上述2种计算方法。

在实际调参过程中,Q值会影响程序调参的方法，从而得出不同的参数X和Y。而X与Y会进一步影响整个评估函数中不同参数的权重比，最终得出评估函数的计算最终结果Value。

4 实验测试

首先初始化训练参数。设评估函数模型中待调整的参数X、Y初值分别为5和20。对于训练模型的每次调参操作中，训练次数为10 000次，即模型在每次调参前需要更新10 000次网络Q值。以黑方棋子作为调参测试对象。规定每次自对弈的局数为5局，即若黑方获胜2局以上即可获得奖赏。为了加快调参速度，限制了较浅的搜索深度以及较短的搜索时间。在对弈时，除了双方程序评估函数的参数不同之外，其内部算法和逻辑结构等部分完全相同。

对模型进行第一次调参训练，从中随机抽取并跟踪了6个结点的Q值变换过程，分别为网络第二层的3号、5号结点以及第三层的结点20号、22号、33号和36号结点，结果如图3、图4所示。可见,当训练次数为1 000时，Q值仍处于动态变化之中，在后期开始出现收敛的趋势。而当训练次数达10 000次时，各结点的Q值已处在一个相对稳定的区间内波动，从而可以认为此时的网络已经训练的较为充分。

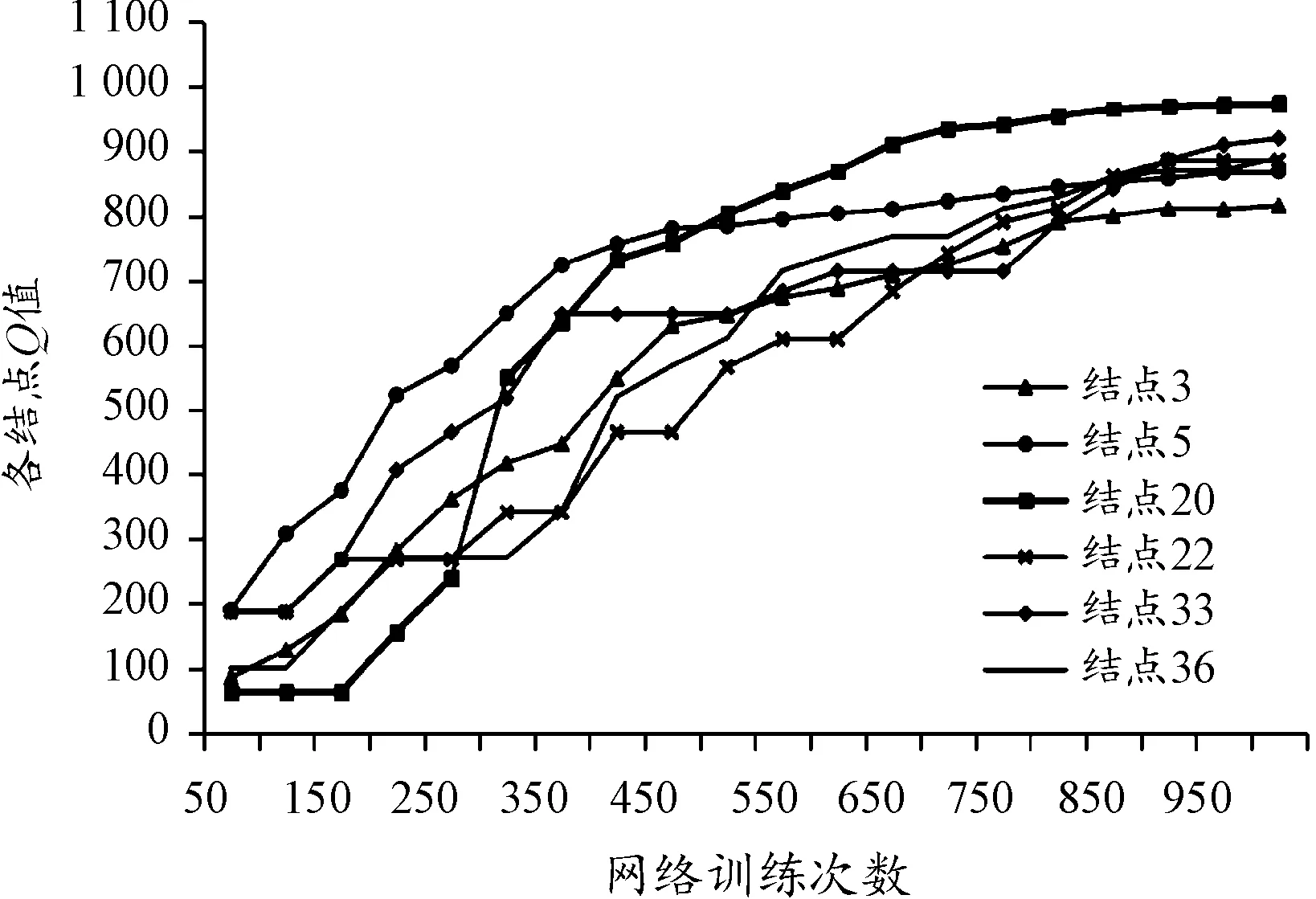
图3 训练1 000次时节点Q值变化曲线

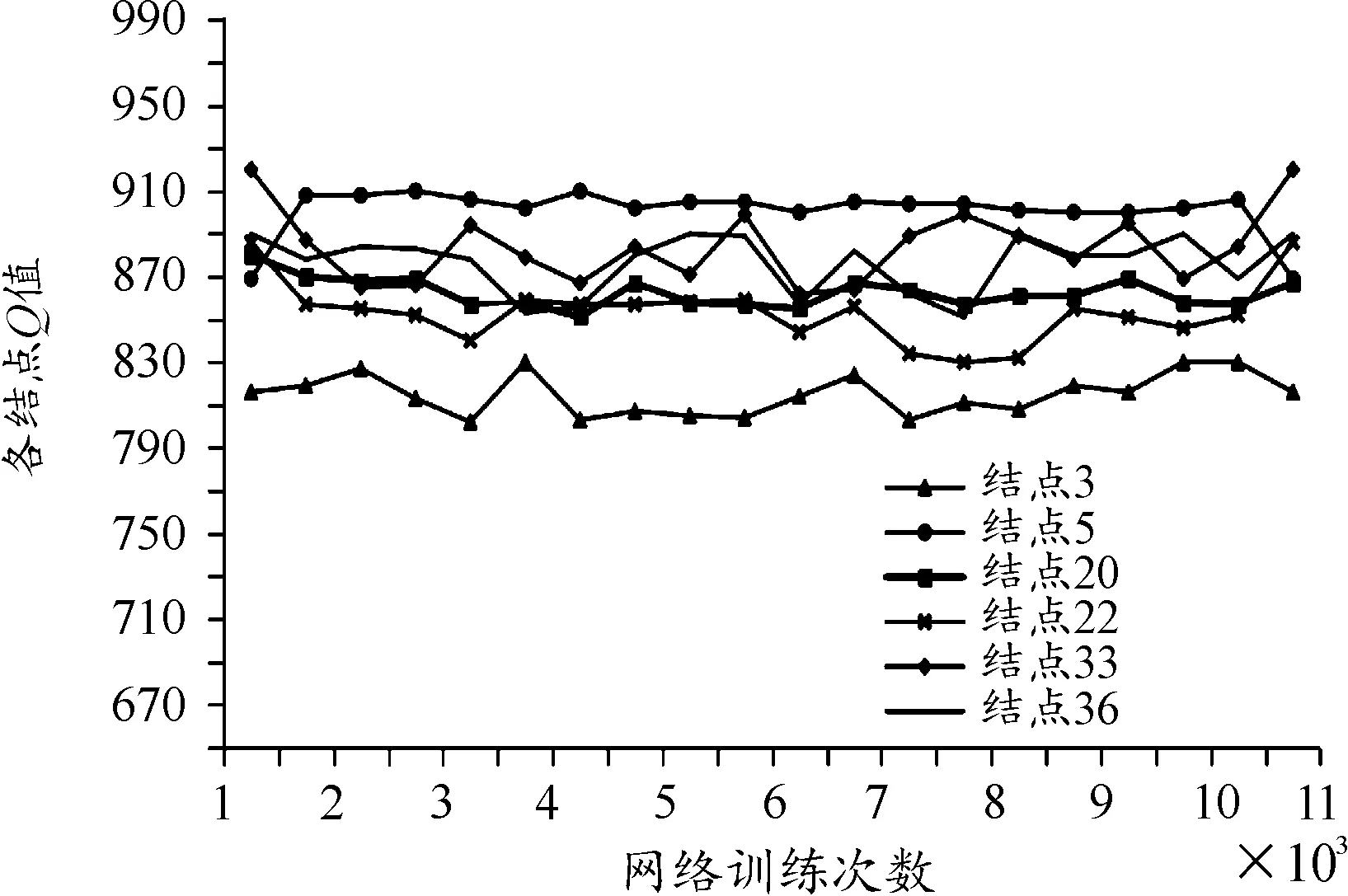
图4 训练10 000次时节点Q值变化曲线

因此，针对本次训练的6个结点而言，得出的行动路线是5号结点至33号结点，最终的调参步骤应是先进行5号结点操作(X=X+C1、Y=Y+C2)，之后进行33号结点操作(X=X、Y=Y+C1)。重复上述调参步骤，进行数次调参后最终参数X与Y的变化情况分别如图5、图6所示。可见，在训练过程中X、Y的值逐渐收敛并趋于稳定。训练结束后，X值由最初的5被调整为3，而Y值由最初的20被调整为19.2。

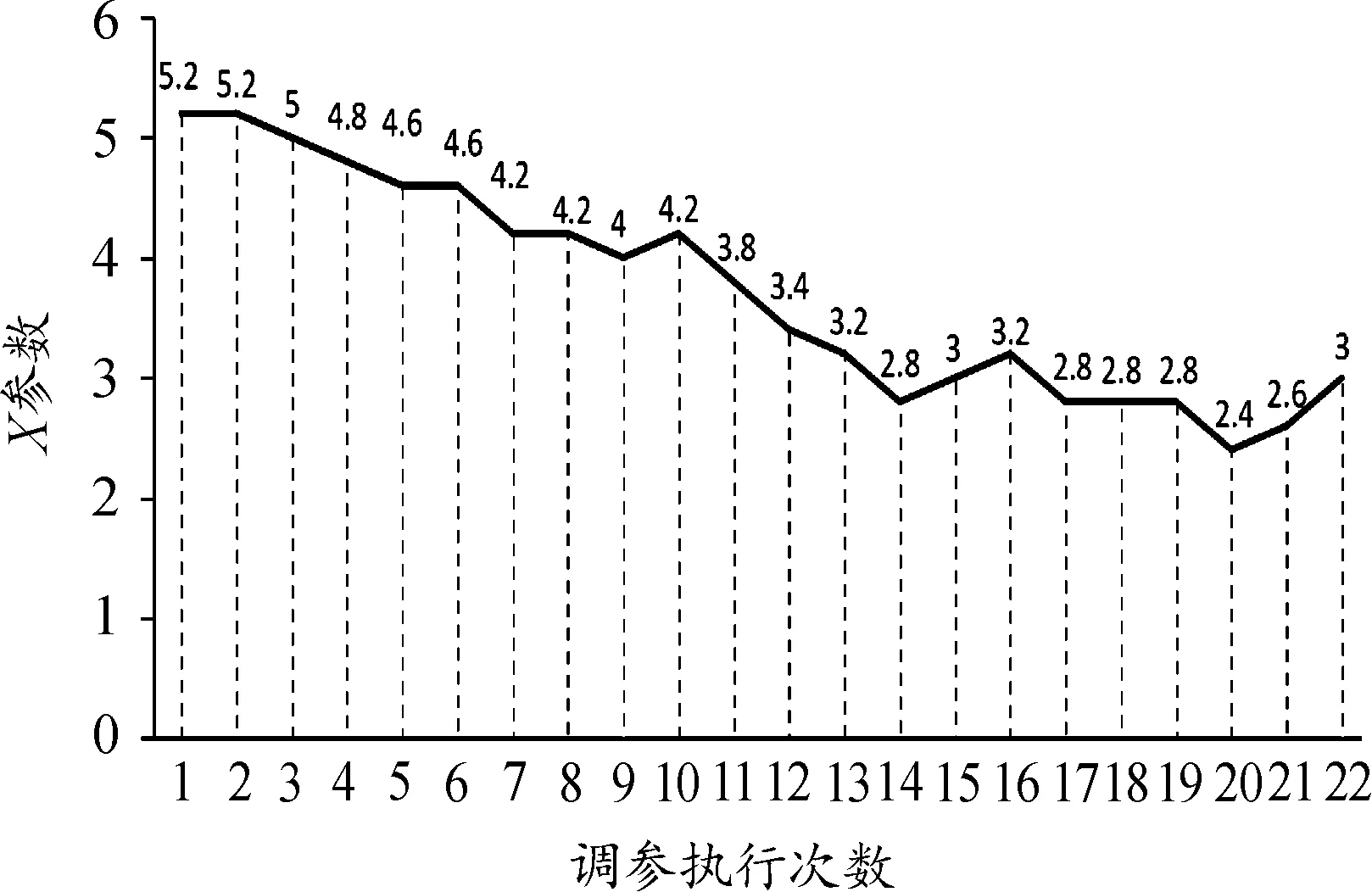
图5 参数X调整情况

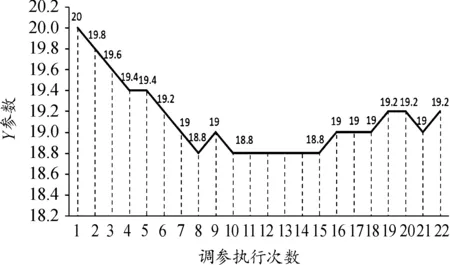
图6 参数Y调整情况

理论上，在单次调参操作中进行更多的网络训练(即Q值更新)，程序会选择更加合理的调参行动。然而，每次的调参操作对整体评估函数参数的影响是有限的，且每次执行调参后该网络模型都会被重置初始化。因此，在单次调参中对网络进行过多的训练，性价比显得不高。应结合具体的硬件设备和程序本身来确定一个较为合适的单次调参训练次数，尽可能多地完成调参操作，而避免花费大量的时间在仅仅一次的调参操作内。这样，调参的效果会更加明显，调参的整体效率也会更高。

为验证程序整体棋力水平，该程序参加了中国计算机博弈锦标赛。在比赛过程中，相较其他程序而言，其最大特点是对棋盘空位的利用率很高，能更有效地利用自己目前所占有的区域。在与强队进行比赛时，双方棋力相差不大，我方凭借对棋盘空位的充分利用，最终靠细微优势打败对手，如图7所示，黑棋为我方棋子。最终该程序取得了季军的成绩，说明该程序棋力优于大部分传统博弈程序，同时调参的效果也得到了体现。

图7 对弈终局局面

5 结论

结合Q学习的思想，构建了一个亚马逊棋评估函数自调参强化学习模型。克服了传统人工调参方式耗时耗力的缺点，实现了调试的自动化，同时对棋力的提升起到了一定效果。该思路不仅适用于亚马逊棋的调参工作，对于类似的完全信息博弈类棋种依然适用。