摩托车非共面与共面振动的多目标优化

黄泽好，童 勇

(重庆理工大学 车辆工程学院， 重庆 400054)

0 引言

摩托车消费需求从小排量通勤代步逐渐转变为中大排量比赛娱乐，影响其操控稳定和驾乘舒适的振动问题日渐受到关注。摩托车振动按振动维度分为影响驾乘舒适的共面(In-plane)振动和影响操控稳定的非共面(Out-of-plane)振动[1]。共面振动是指所有如垂向和俯仰振动等发生在同一平面内的振动。非共面振动则是垂直于摩托车纵向平面的振动，主要包括前轮绕转向轴往复转动的摆振(wobble)，以及整车侧倾和横摆复合的类似蛇形运动的迂回摆动(weave)[2]。

为减小共面振动，徐中明等[3]通过多目标优化获得了同时改善俯仰和垂向振动的最佳悬架刚度和阻尼；彭帅[4]提出能减小垂向振动的具有最佳阻尼特性的电磁阀式可变阻尼悬架，但成本昂贵；Kaul[5]引入发动机悬置有效隔离垂向振动传递；冉险生等[6]考虑前叉后倾角等更多悬架参数，结合近似模型和优化方法寻找到更佳减振效果的悬架参数值。

为改善非共面振动，Evangelou等[7]通过增加转向阻尼有效提高了摆振模态稳定性；Ramirez等[8]通过根轨迹分析指出降低前叉扭转刚度能够提升摆振稳定性，但对迂回摆动稳定性不利。冉险生等[9]通过优化悬架参数实现了摆振和迂回摆动模态稳定性的全面提升。虽然以往研究改善了振动，但仅考虑了非共面振动或者是共面振动的单一问题优化而忽视了另一振动是否恶化。

本文以某摩托车为对象，建立人-车-路系统仿真模型，利用根轨迹分析其非共面振动稳定性。以改善非共面振动稳定性同时减小共面振动为目标，结合灵敏度分析、多目标遗传优化和熵权优劣解距离决策法确定悬架参数最佳设计值，从而提升摩托车操控稳定性和驾乘舒适性。

1 人-车-路系统模型的搭建

1.1 摩托车动力学模型的建立

某摩托车部分参数如表1所示。将整车分为车身、转向头、前后悬架和前后车轮6个刚体，在Bikesim工具中根据结构参数和性能参数等进行参数化建模，如图1所示。

表1 摩托车部分参数

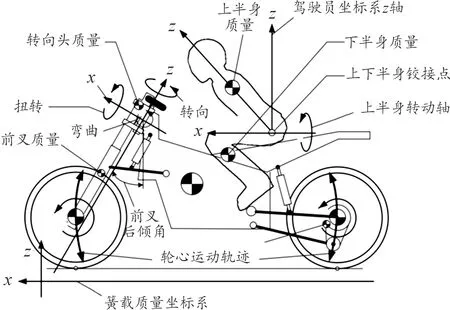
图1 摩托车整车模型示意图

整车模型共包含13自由度，如表2所示。

表2 整车模型自由度

1.2 驾驶员模型的建立

建立驾驶员模型以模拟实际操控环境，其一模拟驾驶员驾乘位置和姿态变化，其二模拟驾驶员对转向头的转向控制。研究表明，驾驶员姿态变化相对转向控制对摩托车的操控影响很小[10]，因此，将驾驶员考虑为刚体连接在车身上而忽略其姿态变化，仅考虑驾乘位置和人体质量分配。驾驶员质量设定70 kg，按NASA建议的62/38比例分配上下半身质量，驾驶员驾乘模型如图2所示。

图2 驾驶员驾乘模型示意图

驾驶员控制车辆采用基于预瞄路径跟随的PID闭环侧倾角控制方法[11]，控制流如图3所示。

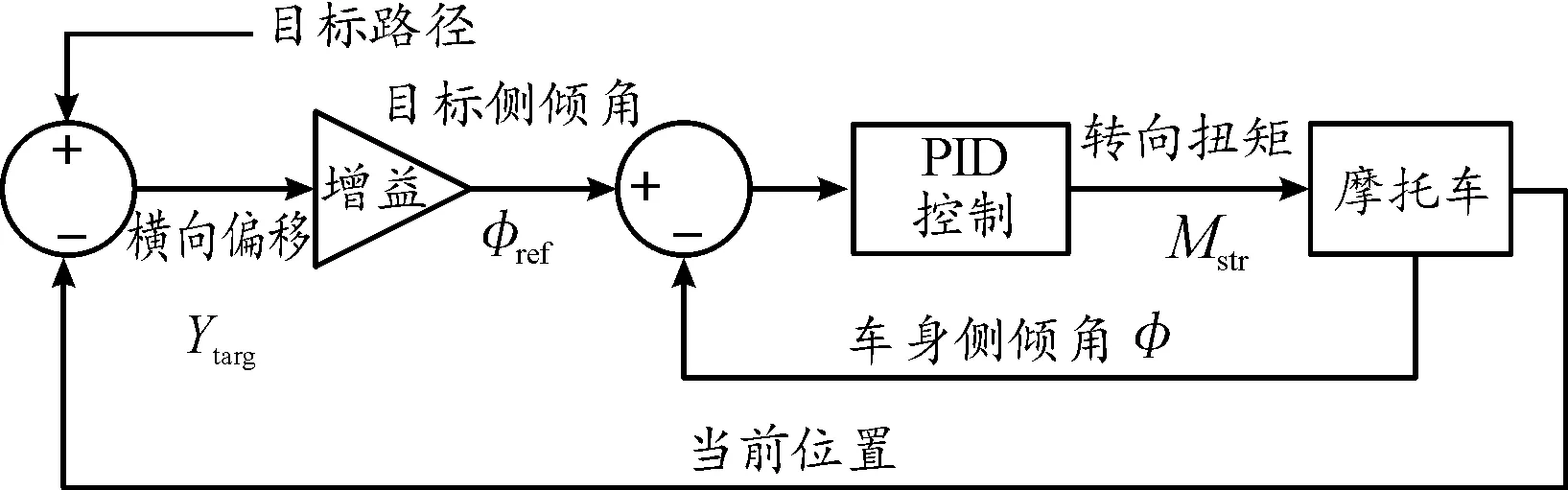
图3 驾驶员模型控制流框图

当摩托车偏离目标路径时，首先计算一个预瞄时间后的目标路径与当前行驶路径之间横向偏移量，然后通过横向偏移量获得摩托车驶回目标路径所需的目标侧倾角，最后以目标侧倾角与当前车身侧倾角的误差作为PID输入从而生成施加于转向手把的转向力矩以调整行驶方向，通过不断调整摩托车转向和侧倾状态以减小横向偏移和侧倾误差，从而使摩托车驶回目标路径并维持路径跟随。目标侧倾角与转向力矩计算如式(1)和式(2)所示。

(1)

式中：Kp、Kr分别为横向偏移增益和稳态侧倾增益；ρtarg为预瞄点处的路径曲率。

(2)

其中

P=p1+p2·Vx

I=i1+i2·Vx

D=d1+d2·Vx

(3)

1.3 路面模型的建立

为模拟实际行驶环境，根据国内路面条件应用傅里叶逆变换法建立三维C级路面模型[12]。

(4)

式中：S[p,q]为二维离散路面功率谱密度；n0为参考空间频率。

根据车速范围30～160 km/h(vmin～vmax)，为使路面频率范围足以覆盖摩托车振动固有频率范围0.5～30 Hz(fL～fH)，设定空间频率上下限值。

(5)

利用傅里叶逆变换法处理S[p,q]得到三维路面高程，如图4所示。

将摩托车13自由度动力学模型、驾驶员控制模型和三维路面模型集成为人—车—路系统模型，如图5所示。

图4 三维C级路面高程模拟图(部分)

图5 人—车—路系统仿真模型示意图

2 非共面振动稳定性分析

为直观反映非共面振动的摆振和迂回摆动模态的稳定性，利用根轨迹法进行研究。根轨迹法是通过图解方法表示线性系统特征根与系统某一参数关系的方法[13]。特征根表征系统受外界扰动的稳定性，其一般为复数形式：s=σ±jωd。其中，特征根实部σ为相关振动模态的稳定裕度，为正时，表示振动因发散而不稳定，为负时，表示振动因衰减而稳定。

图6为该车直线行驶速度30～160 km/h的非共面振动的摆振模态(wobble)和迂回摆动(weave)模态根轨迹曲线，图中圆点大的表示车速大，速度间隔为10 km/h。由图6可知，在30～160 km/h车速范围内直线行驶时，该车迂回摆动模态特征值实部小于0，均处于稳定区域，说明迂回摆动始终稳定。而摆振模态在中低速范围(30～90 km/h)内特征值实部为正，处于不稳定区域，即出现负模态阻尼现象导致摆振发散。但当超过临界车速90 km/h时，该摆振趋于稳定且车速越高越稳定。

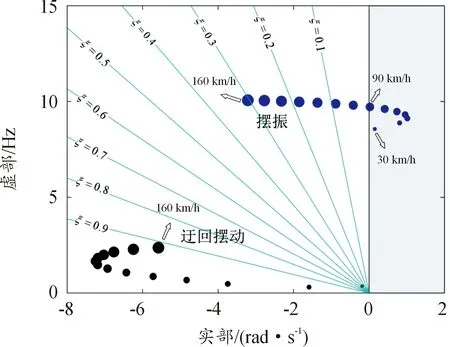
图6 直线行驶工况的根轨迹曲线

3 非共面与共面振动的多目标优化

悬架参数是影响非共面振动的主要因素，为消除非共面振动不稳定现象需对悬架参数进行优化匹配设计。同时，考虑影响驾乘舒适性的共面振动，通过多目标优化提升摩托车整体行驶性能。

3.1 优化对象的选取

采用拉丁超立方试验设计方法筛选出显著影响非共面和共面振动的悬架参数作为优化对象。首先初步确定前后悬架共13个独立设计参数及其取值范围，如表3所示。

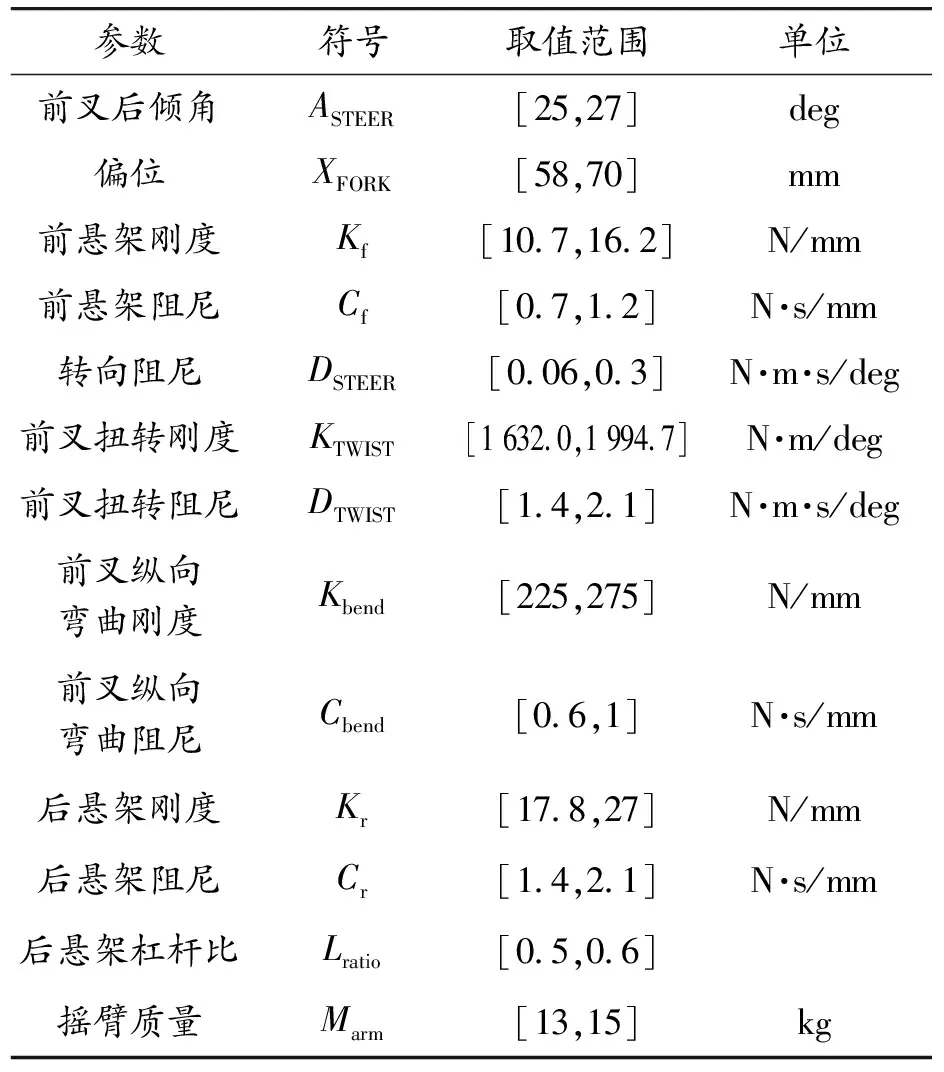
表3 悬架参数与取值范围

为保证筛选结果可靠，采用2倍最小采样数(m+1)·(m+2)/2[14]，其中m为初选悬架参数个数，计算得采样数为210。选取60 km/h直线行驶典型工况，计算非共面振动的摆振和迂回摆动模态特征根实部值以及共面振动的垂向和俯仰振动加速度均方根值，通过系数法获得悬架参数对非共面和共面振动的贡献率，如图7、8所示。

图7 悬架参数对非共面振动的贡献率

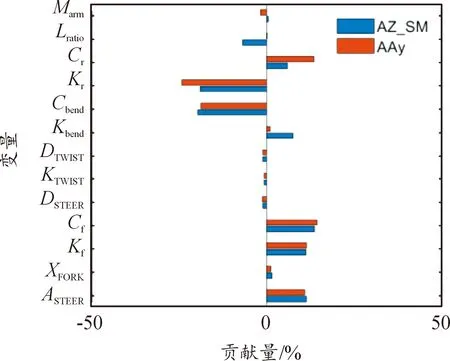
图8 悬架参数对共面振动的贡献率

由图7、8可知，杠杆比Lratio、转向阻尼DSREET、偏位XFORK、前叉后倾角ASTEER、前后悬架刚度和阻尼(Kf、Kr、Cf、Cr)和前叉弯曲阻尼Cbend共9个悬架参数对非共面和共面振动有显著影响，因此,选其为优化对象。

3.2 多目标优化数学模型的建立

为确保非共面振动稳定性，以摆振和迂回摆动稳定的临界状态为约束条件，同时将摆振和迂回摆动模态特征值实部值作为目标函数并期望其值尽可能小以追求更优的稳定性。为降低共面振动，引入额外的目标函数——摩托车质心处的垂向和俯仰加速度均方根值。此外，考虑到前后悬架撞击限位装置而威胁驾乘安全问题，引入悬架动挠度约束。选取60 km/h直线行驶作为典型优化工况。寻求9个悬架参数的最佳设计值，构建多目标优化模型，如式(6)所示。

findx=(Lratio、XFORK、ASTEER、

DSTEER、Kf、Kr、Cf、Cr、Cbend)T

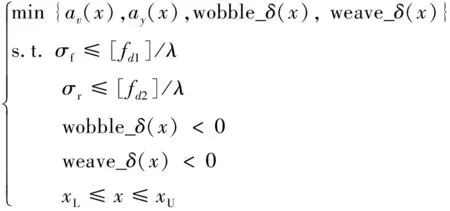
(6)

式中:av、ay分别为摩托车在C级路面激励下以60 km/h直线行驶时，整车质心处的垂向和俯仰加速度均方根值；wobble_δ、weave_δ分别为摩托车摆振和迂回摆动模态特征值实部最大值；σf、σr分别是前后悬架动挠度标准差；[fd1]、[fd2]分别是前后悬架限位行程，其值分别为33 mm和21 mm，λ为正态分布比值，其值为3[3]。xL、xU分别为设计参数取值的下限和上限，如表3所示。

3.3 联合仿真优化平台的搭建

由于每一次优化迭代均需调用Bikesim进行摩托车动力学仿真运算，以及调用Matlab对仿真结果加以数据处理。人工操作繁琐且易操作失误。因此,应用计算机辅助优化平台Isight集成Bikesim、Matlab以实现多目标优化的自动化，如图9所示。

图9 基于Isight环境的自动优化平台示意图

3.4 优化与决策

采用先优化后决策的方法。首先应用遗传算法NSGA-Ⅱ实现非共面和共面振动的多目标优化，设定种群规模60，进化代数40，交叉率0.9，交叉分布指数10，变异分布指数20。优化模型在Isight平台经过2 400次迭代后获得317个可供选择的pareto最优解。图10给出了各pareto最优解对应归一化目标函数间的关系。

图10 pareto最优解(部分)

图10中，每一条折线对应一个pareto最优解，可以看出任一pareto最优解均无法同时满足4个目标最优。为此，利用熵权优劣解距离法[14-16]计算pareto最优解与理想最优解的贴近度，从而对pareto最优解的选择进行决策以确定最终悬架具体设计参数值。pareto解的贴近度计算结果表明：第81个解的贴近度最高，为0.93，因此，以第81个pareto解确定为非共面与共面振动优化的全局最优解。优化前后的悬架参数值如表4所示。

表4 优化前后悬架参数

悬架参数优化前后的优化目标值如表5所示。

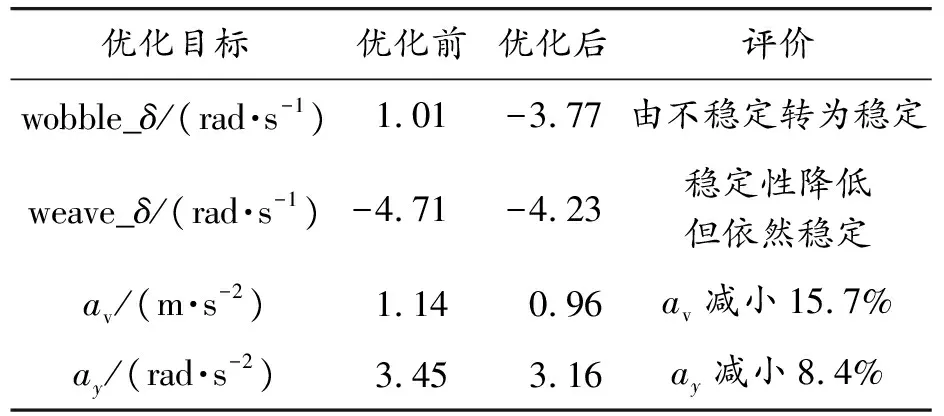
表5 优化前后对比结果

由表5可知，以车速60 km/h直线行驶时，优化后摆振模态特征根实部由1.01变为-3.77，说明该模态由不稳定转为稳定，而迂回摆动模态特征根实部由-4.71变为-4.23，虽然有所增大，但依然处于可以接受的稳定区域。同时，共面振动的垂向和俯仰振动加速度均方根值分别由优化前的1.14 m/s2和3.45 rad/s2减小到优化后的0.96 m/s2和3.16 rad/s2，分别减小了15.7%和8.4%，优化效果较好。为验证优化后悬架参数在其余车速时的效果，绘制非共面振动摆振和迂回摆动模态根轨迹，如图11所示。

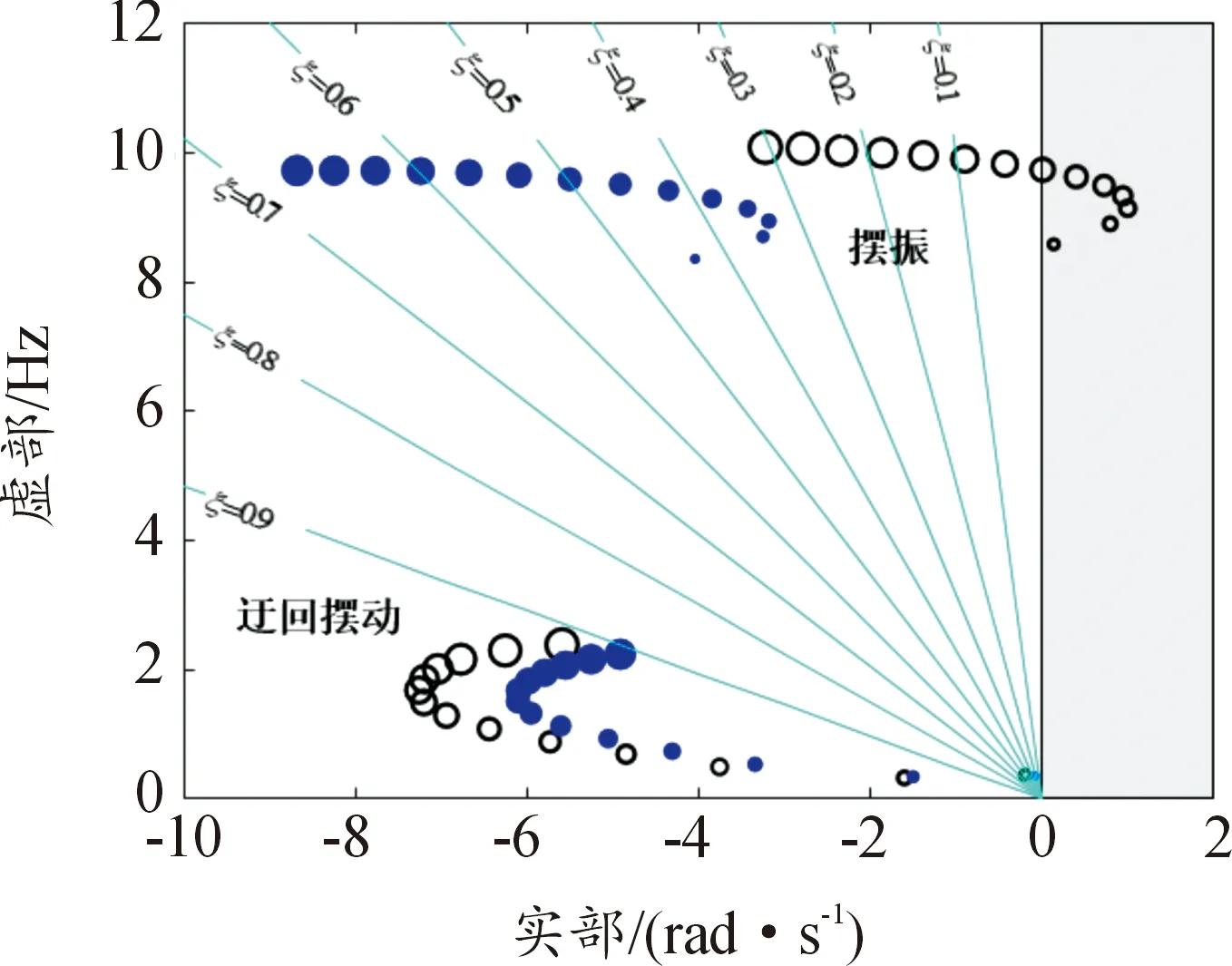
图11 优化前后非共面振动根轨迹曲线

由图11可知，优化后的摆振模态在其余车速直线行驶时均未出现稳定性恶化，虽然迂回摆动模态稳定性比优化前均有少量变差，但是依然处于可以接受的稳定区域。此外，由于行驶工况变化对路面激励下共面的垂向和俯仰振动响应最直接作用是改变路面功率谱输入。路面位移功率谱密度表达式如式(7)所示。

(7)

由此可知，路面输入与行驶车速u和道路级别Gq(n0)线性相关，因此，悬架参数优化后的摩托车即使以不同车速行驶于同一等级路面，其共面的垂向和俯仰加速度均方根值同样能达到最优。因此，优化后悬架参数值能全面提升摩托车整体行驶性能。

4 结论

通过建立摩托车人—车—路系统仿真模型，应用根轨迹分析发现某摩托车非共面振动的摆振模态在中低速范围内负模态阻尼不稳定。通过多目标优化以实现非共面振动稳定并降低共面振动。结果表明，以60 km/h直线行驶时，非共面振动的摆振模态和迂回摆动模态均实现稳定，且共面的垂向和俯仰振动加速度均方根值较优化前减少了15.7%和8.4%。其余车速工况也取得了较好的优化效果。