培养学生度量意识 促进数学量感发展

唐玲　丘燕飞

量感一般是指对事物的可测量属性以及大小关系的直观感知。建立量感，需要学生知道度量的意义，能够理解统一度量单位的必要性;能对真实的情境选择合适的度量单位进行度量，在同一度量方法下进行不同单位的换算;初步感受度量工具和方法引起的误差，能合理得到或估计度量的结果。建立量感还有助于养成用定量的方法认识和解决问题的习惯，是形成抽象能力和数学应用意识的经验基础。

一、建立丰富表象，感知“量”

北师版教材在每一个新知识点展现时都注重创设一个有趣的情境，其设计意图是链接学生已有的生活经验，开启已有的认知表象，利用已有的表象、生活经验来探究新的知识。特别是丰富的表象可以让静态的结论及其隐含的意义动起来，提高学生认知过程的质量。

以“计量单位”教学为例，其教学目标是培养学生的度量意识，发展量感。其中，量感的培养有助于锻炼学生的数学思维，提高观察能力以及估测能力。

（一）在体验中感知量的变化

以“认识质量单位克和千克”为例，在新课讲授之前，可以引导学生进行实践调查活动。通过去超市调查采购、对家人进行采访，拍摄记录下哪些物品使用克、哪些物品使用千克来表示重量。此外，还可以通过称一称、掂一掂来感受不同物体的重量。通过这样的活动，学生实际体验了超市里1千克和3千克一桶装的洗衣液、5千克和2千克一桶装的食用油以及100克的芝麻和200克的绿豆拿在手上分别是什么感受，认识到了克与千克的不同之处。

通过课前的实践活动，克与千克对于学生来说不再是冷冰冰的几个字。通过课前实践感知，打通了数学与真实世界的联系，让学生在脑海中积累了丰富的表象;通过感受量的变化，初步发展了克与千克的量感，积累了宝贵的直接经验。

（二）在操作中感知量的多少

在学生初步感知了克与千克的量感之后，教师在课堂上可以创设相关的教学情境，让他们尝试着用自己建立的量感经验解决生活中遇到的一些实际问题，培养度量意识，提升应用量感的能力。如为了更好地感受1千克有多重，这一环节我在课堂上为学生提供了花生、大豆、苹果等食品，还为每个小组提供了1千克的糖果。让学生开展小组活动，要求在不使用称的条件下想办法估测出1千克的食品来。学生在思考、讨论和尝试的过程中慢慢总结出方法：一只手拿着1千克的糖果，一只手拿着装有食品的塑料袋，将1千克的糖果作为参照，通过增减另一边的物品，再反复掂量、比较。最后，竟然有很多小组的学生成功地估量出了接近1千克的食品。这样，学生在反复掂量的过程中加深了对1千克的具体量的认知和感受。

（三）在生活中感知量的应用

学生学习量感不是一蹴而就的，因为量感是一种直观的、定量刻画的能力，所以需要教师对这样的内容有一个长程的设计。在新课学习过的基础上，要设计相应的实践活动来巩固、实践、提升学生的量感。如在学习完“克与千克”之后，可以设计这样的实践活动：请挑选5种物品，每一种物品的重量分别是50克、100克、150克、200克、500克，使这5种物品的重量加在一起是1千克。学生通过一次次耐心地测量，感受到了克与千克之间的关系，避免了一些如“一盒牙膏重约50千克”“爸爸的体重400克”等令人啼笑皆非的错误，发展了度量意识和量感，体验到了“量其实就是计量单位不断地叠加的”这一内涵。学生利用量的知识来解决问题，也体验到了量感的数学本质。

二、开展实验教学，体验“量”

实验教学不仅可以将一些抽象的数学知识、概念等加以直观化、具体化，而且有利于学生对数学知识的理解，促使他们能够透过数学实验去领悟数学知识的本质。实验教学的目的之一是提高学生对数学知识的理解能力，促使他们能够通过相应的数学实验发现、了解、掌握数学知识之间的内在规律或联系，并在培养数学思维能力的同时，达到提升数学素养的目的。

数学教学中的实验是指在数学思想和数学方法的指导下，在教学过程中，让学生通过借助一定的仪器或是一些技术手段，对实验素材进行“数学化”的操作来“学数学”“用数学”，最终达到“理解数学、建构数学”的一类数学学习活动。学生在实验教学过程中，通过操作、观察、分析、猜想和推理等数学活动，能使度量意识得到提升，量感得到培养。

（一）在具体转化中体验“量”的本质

在“体积与容积”这一节课的教学中，可以开展“比大小”的实验活动。如比较土豆和红薯谁的体积大？在小组实验活动过程中可以为每个小组准备大小不一样的瓶子、土豆、红薯、量杯、水等。有的小组通过选择两个一样的瓶子装一样多的水，再将土豆和红薯分别放在两个瓶子里，发现土豆所在瓶子的水面上升得高，于是得出结论：土豆的体积大。有的小组选择将两个一样的瓶子都装满水，再分别将土豆和红薯放进两个装满水的瓶子里，两个瓶子里都会有水溢出来，将溢出来的水再分别装进两个量杯里，通过比较溢出水的多少来判断土豆和红薯的体积。

无论哪种方法，都是将抽象的量转化成具体的、可视的量来感知，都是实验小组成员通过讨论、尝试、推理、验证得出的结论。在实验的过程中，学生在推理验证中体验了量感、在操作尝试中感悟了度量。当学生亲手对数学实验项目进行操作时，他们的学习行为就从单纯的“动作”过渡到了对“量的本质”的理解。

（二）在抽象建模中体验“量”的大小

通过建模的方式能有效帮助学生进行学习。在建模时，学生从最开始的实物性建模，慢慢转变为半实物、半抽象性建模，最后升级为抽象性、创造性建模。

在教学“认识立方分米”时，可以这样对学生进行引导。

师：刚才我们一起学习了什么是1立方分米，现在请大家小组合作来做一做1立方分米，说一说1立方分米。

组1：我们先用100个1立方厘米的小正方体摆成1层，再摆9层，一共摆10层就是1立方分米，通过1立方厘米认识1立方分米。

组2：我们是用摆与想象相结合來认识1立方分米，先摆1层，再摆10层的高度（每层摆1个）想象1立方分米。

组3：我们组是通过想象一个棱长为1分米的正方体从而想象出1立方分米的大小，最后在我们身边寻找和 1 立方分米差不多大小的物体帮助感受1立方分米的大小。

师：请你们闭上眼睛，想象你认为的1立方分米的大小。请看一下眼前这个1立方分米的物体，你觉得这个物体的大小和你之前想象的一样吗（学生表示物体比自己想象的大、或小、或一样大）？

通过这样的学习，学生发挥想象力，通过已有经验寻找生活中的1立方分米或构建出1立方分米的模型。在这个教学过程中，我始终将学生放在学习的主体地位，使他们由被动地接受知识变成主动探究，大大激发了他们学习的主观能动性。学生在活动中利用自己各方面的感官，从具体到抽象建立数学模型，体验了量的大小。

三、联系不同维度，培训“量”

要联结不同维度的量感，可以通过将“长方体的认识”这节课嵌入到数学知识的整体框架中，让知识结构化、整体化、系统化。这样，有利于学生量感的长远发展。这个过程，不仅要关注量感知识的掌握、思维的培养、思想方法的渗透，更要聚焦关键能力的培养，引导学生真正学会“用量感的眼光观察世界，用量感的思维思考世界，用量感的思想创造世界”，使其数学素养得到提升。

（一）在横向宽度中领悟量感的生活价值

在学习“面积单位”这一课时，因为学生在课前已经有了厘米和分米知识的基础，这节课的学习又是为了后面学习体积奠定基础，所以对这节课内容地扎实掌握非常重要。为了帮助学生横向打通“1平方分米”多个方向之间的密切联系，建立“1平方分米”的量感，课堂上我们引领他们开展了以下关于“1平方分米”的小活动。

【活动一】看一看 1 平方分米。通过向学生呈现各种不同形状的大小都为“1 平方分米”的图形，让他们明白：不只是只有边长为1分米的正方形面积才是1平方分米，不规则图形也可以。

【活动二】说一说 1平方分米。让学生结合日常生活，说一说现实生活中有哪些1平方分米。有的学生认为，手机屏幕的大小可能是1平方分米;还有的学生认为，橙子的大小有1平方分米。

【活动三】思一思1平方分米。在前面两个活动的基础上，放手让学生构思，根据自己所学的知识来创造1平方分米的图形。有的学生说：“边长 10厘米的正方形面积就是 1 平方分米”;有的学生说：“长50厘米，宽2厘米的长方形面积也是 1 平方分米”。

【活动四】画一画1平方分米。经过前面3个活动，学生对“1 平方分米”已有了足够的认识和感知，通过这个活动，让学生将自己理解的“1平方分米”呈現出来，进一步建构“1 平方分米”概念，领悟“1 平方分米”的大小。

（二）在纵向深度中领悟量感的数学价值

学生在长度、面积、体积单位的起始课“认识厘米”“认识面积单位”“认识体积单位”的学习中已经深刻地感受到了统一度量单位的必要性，积累了一定的度量经验和量感。从一维到三维，对图形的大小进行定量刻画时，其在知识本质和思考方法上有很多类似之处。所以，在教学设计时可以统筹设计这三节课，将它们统整到一个“内容群”里，让学生建立这种从一维到三维的量感思维。

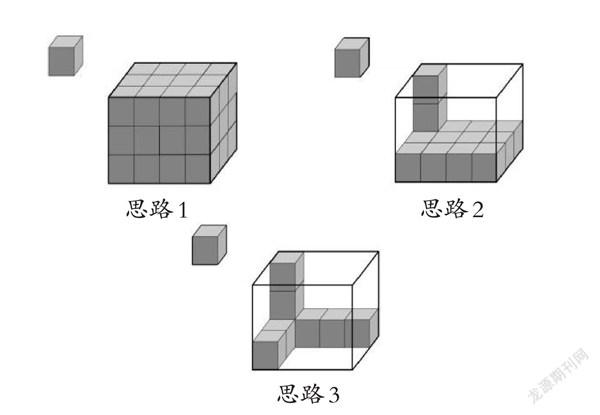
在学习五年级下册“长方体的认识”这节课时，可以结合学生已经拥有的多维量感进行教学设计，让他们利用已有的度量思维以及量感储备自主探究并解决问题。可以设计“长方体神秘魔盒”的情境，引导学生探究它的体积。课堂上可以小组合作，利用若干个棱长1cm小正方体，测量这个长方体的体积。可以算一算摆的长方体一排有几个，摆了多少排，摆了多少层，一共用了多少小正方体。学生可能会出现以下3种思路：

思路1：摆满;

思路2：摆一层和高;

思路3：只摆长、宽、高。

基于三维量感的基础，学生自然而然地想到每排个数、每层排数、一共多少层和总体积之间的关系。顺理得出：长方体体积数=小正方体总数=每排个数×排数×层数。而每排个数相当于长，排数相当于宽，层数相当于高，进而总结概括出：长方体的体积=长×宽×高。

（责任编辑：杨强）