基于改进狮群算法的低碳冷链配送中心选址研究
2022-02-07黄志锋张孝文张文敏任志豪
张 聪,姚 佼,黄志锋,张孝文,张文敏,任志豪
(上海理工大学 管理学院,上海 200093)
0 引言
当前,为了有效应对疫情防控,也给医药冷链物流提出了新挑战。冷链配送中心的选址优化是研究冷链物流资源配置的基础问题之一。因此,在公共卫生事件不定时突发情况下,建立合适的冷链物流配送中心显得十分重要。
近年来,多位学者就配送中心选址规划问题进行了深入研究。郭俊佳[1]的研究认为目前配送中心布局不够完善,缺乏应对突发情况的运营经验,其中配送中心分布不合理不能满足需求点需求是配送“断链”的主要原因。王思静[2]的研究认为冷链物流配送最重要的是在规定的时间内能否把药物送到各需求点。因此,引入了物流服务响应概率这一概念,以物流服务响应概率最大化为目标构建模型,并且进行实例验证。Wang 等人[3]从经济效益、社会效益和环境效益三个方面建立了冷链物流网络的生物目标数学模型。提出多目标超启发式算法优化用来解决这个多目标问题。通过对比研究发现,该算法比NSGA-II 具有更好的整体性能。以便为物流公司选择合适的冷链物流配送网络。Liu 等人[4]研究了西北地区冷链物流选址问题,建立了基于最短运输距离的数学模型,对西北地区冷链物流的资源利用、区域物流发展、冷链产品需求扩张等具有重要的指导意义。
狮群优化(Lion Swarm Optimization,LSO)算法是刘生建等人[5]模拟狮王保卫领土、母狮协同捕猎,捕捉后的猎物统一交由狮王进行分配、幼狮跟随学习的自然行为,提出一种新型群体智能优化算法。目前已经成功应用于汽轮机热耗模型预测、云计算调度策略优化、配电网优化、BP 神经网络模型房价预测等领域中。然而,与其他群体智能优化算法类似,标准的LSO 算法也存在全局搜索能力差、易于“早熟”等缺点。针对这些缺点,学者们提出了不同的改进策略。吴忠强等人[6]通过引用自适应参数和混沌搜索,对狮群算法的局限性进行了优化。汪婵婵[7]为了提高算法的收敛速度和准确性在狮群算法中加入了邻域搜索结构、非线性扰动因子等。赵杨等人[8]在狮群算法中引入驱逐和变异操作,提高狮群算法的多样性。但以上改进的LSO 算法都很难在加快算法收敛度和避免陷入局部最优方面取得平衡。
因此,在传统狮群算法的基础上,本文通过引入调节因子和高斯变异对传统狮群算法进行改进,提高算法寻优和跳出局部最优解的能力,将ILSO 算法应用在配送中心选址问题上,在其中考虑碳排放成本和物流成本,并将ILSO 算法的选址结果和LSO算法、GA 算法进行对比分析,得出ILSO 算法在配送中心选址问题方面,相比LSO 算法和GA 算法具有一定优越性。
1 模型构建
1.1 问题描述与条件假设
现经过专家评审,提出m个具备专业化、系统化的备选医药冷链配送中心进行统一的分拣及配送工作方案,需要从中选出合适的配送中心进行建设,以物流服务响应概率为约束条件,保证传统配送成本最低、碳排放成本最低。模型相关假设如下;
(1)供需双方的位置已知,所有备选配送中心已经过专家审核进行确定。
(2)假设配送车辆正常行驶,不考虑因拥堵或者车辆故障产生的碳排放成本。
(3)不考虑供应商和需求点产生的碳排放成本。
1.2 变量和参数设定
m为备选配送中心个数;n为需求点个数;xij为从供应点i到配送中心j的运输量;xjk为配送中心j到需求点k的运输量;dij为供应点i到配送中心j的运输距离;djk为从配送中心j到需求点k的运输距离;Rk为需求点k的需求量;p为单位药品运输成本;vij为车辆从供应点i到配送中心j的平均运输速度;vjk为车辆从配送中心j到需求点k的平均运输速度;Sj为配送中心j的单位运营成本(存储及保养费用);O为配送中心j的固定建设成本;N为系统总成本;tij为药品从供应商i到配送中心j所需时间;tjk为药品从配送中心j到需求点k所需时间;tj为配送中心j处理药品消耗的时间;tmax为需求点能接受的最晚时间;M表示备选配送中心处理货物能力;B表示备选配送中心的运出量;λ为碳税价格。
1.3 传统配送中心选址成本
传统配送中心选址成本主要包括备选配送中心的固定建设成本、运营成本和运输成本,用公式表示为;

1.4 低碳配送中心选址成本
低碳方面,在冷链物流过程中,需要将温度保持在较低的水平,会产生大量的能源消耗和二氧化碳。因此,参考文献[9]中研究得到的配送中心产生的碳排放成本,具体公式为:

其中,EEj为所消耗的电能(单位:MWh);δ1为电能的碳排放因子;所消耗的燃油量为Wjkg;燃料的低位发热值为μ2;燃料的单位热值含碳量为μ3;燃料的碳氧化率为μ4;Cj为物流配送中心j处理单位产品的碳排放量;Dj为配送中心j的吞吐量;(Dj)w为假设凹函数;w属于{0,1}。
配送过程中碳排放量,根据Zhang 等人[10]碳排放量的测算思路,可由式(3)进行计算:

其中,E(v)表示车辆以速度v行驶1 km 的碳排放量。这里的系数(g,a,b,c,h,e,f)是由车辆类型和车辆消耗能源结构决定的。冷藏车相关参数依次为(429.51,-7.822 7,0.061 7,0,0,0,0)。
根据实际测算,冷藏车每公里消耗的燃料是一般配送货车的1.15~1.20 倍[10]。基于此,结合陶志文等人[11]的研究可知,“相对碳排放量测算方法”对普通货车和冷藏车设置权重系数,普通货车权重系数为0.4,冷藏车权重系数为0.6,进行加权计算后得出其碳排放量,分别见式(8)和式(9):

综上,配送过程中产生的碳排放成本N3为;

1.5 物流服务响应概率
在众多约束条件中,医药冷链配送的及时性尤为重要,以往文献只考虑在时间窗约束下药物是否能按时送达到需求点,较难体现出医药冷链物流的动态性和及时性。因此,结合文献[2]引入物流服务响应概率这一概念。以物流服务响应概率为约束条件,建立冷链物流配送中心。
物流服务响应概率指的是在规定时间内将药品从配送中心j送到需求点k的概率,记作Pjk,则:

其中,F(vjk) 表示车辆从配送中心j到需求点k的速度函数,服从正态分布:vjk~N(ζ,φ2),则:

由此可以推得配送中心对多个需求点的物流服务响应概率PS的计算公式:
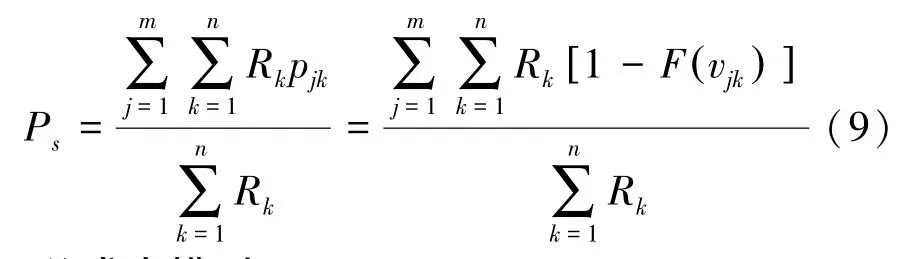
1.6 总成本模型
选址系统总成本N等于传统配送中心选址成本加上低碳配送中心选址成本,如式(10)所示;


其中,式(10)为目标函数;式(11)为配送中心对多个需求点的物流服务响应概率约束条件;式(12)表示配送中心处理货物能力大于等于供应商提供的货物和各需求点相加货物的总和;式(13)表示冷链备选配送中心的运出量大于等于所有需求点总的需求量;冷链配送系统总时间主要包括配送过程中消耗的时间和冷链配送中心处理货物时间tj,式(14)表示冷链配送系统总时间要小于等于需求点能接受的最晚时间。
2 基于改进狮群算法的模型求解
2.1 算法原理
由模型可以看出,本文构建的选址模型属于NP-hard 问题,通常采用启发式算法求得满意解。本文采用启发式算法—改进后的狮群算法(ILSO)对其进行求解。
基础狮群算法(LSO)[5]共分为3 部分。第一部分为狮王,主要负责保卫领土,优先享用食物,狮王代表种群最优解;第二部分为母狮,母狮通过相互配合捕捉猎物,捕捉后的猎物统一交由狮王进行分配;第三部分为幼狮,幼狮共有3 种运动方式,通过这3种不同运动方式增加了算法的多样性。
2.2 算法改进
结合基础狮群算法,本文改进点共有2 个。这里给出解析阐释如下。
首先,本文在基础狮群算法上引入调节因子。基础狮群算法在每次迭代后会更新所有的母狮和幼狮的位置,这可能会导致在前期搜索时,将最优位置的母狮和幼狮进行更新,降低了算法的寻优能力。因此引入调节因子:

其中,ω表示转移母狮和幼狮位置的数量比率;tc为当前迭代次数;Tc为总迭代次数。随着迭代次数的增加,调节因子ω的值增大,这样在算法的前期,更容易保留狮群中母狮和幼狮最优位置。在算法的后期,能转移更多的母狮和幼狮,提高算法的随机性和跳出局部最优的能力。
其次,在狮群算法迭代过程中引入高斯扰动,提高算法的随机性,防止算法陷入局部最优,加快算法收敛速度。此处需用到的公式为:

其中,Xbest(k)表示经高斯扰动后第k代狮群的最优位置,gk表示第k代种群最优位置。高斯扰动在最优解位置进行扰动变异操作得到最新解,加强算法寻优的能力。
至此,研究给出了算法流程如图1 所示。

图1 ILSO 流程图Fig. 1 Flow chart of ILSO
3 算例分析
3.1 改进算法性能验证与分析
为验证ILSO 算法的性能,在仿真平台Matlab 2020b 上进行函数优化测试,选取4 个国际通用测试函数,见表1。

表1 测试函数Tab.1 Test functions
为进一步验证改进狮群算法(ILSO)的性能,将与基础狮群算法(LSO)、遗传算法(GA)进行测试结果对比,其中迭代次数为500 次,函数维度为50 维,种群规模均为100。成年狮比例为0.5;GA 的交叉概率为0.8,变异概率为0.1。各算法独立运行20次,记录结果的平均值、标准差和最优值。实验结果见表2。

表2 测试函数结果对比Tab.2 Comparison of test functions results
算法收敛曲线如图2 所示。对于单峰函数f1、多峰函数f2,ILSO 算法均能求得最优解,且对比LSO 算法和GA 算法,均值和方差更小,改进算法具有较好的寻优能力和稳定性,说明结合高斯变异的狮群算法,具有更好的寻优能力。对于固维函数f3、f4,由于维数的降低,各算法的求解精度都有所提高,但整体上ILSO 更加稳定,求解精度更高。

图2 收敛曲线Fig. 2 Convergence curve
综上,ILSO 在测试标准函数性能方面,优于LSO 和GA。
3.2 算例验证
已知某市K 公司生产某种类型疫苗,用来保证全市疫苗及时供应。并假设该K 公司供应能力无穷大,该公司计划在该市新建配送中心。经过实地勘探需求点并且结合专家建议后,新建配送中心从5 个备选配送中心选出,全市共有20 个需求点。表3 为供应商相关信息,表4 为备选配送中心相关信息,表5 为需求点相关信息。

表3 供应商信息Tab.3 Related information about suppliers
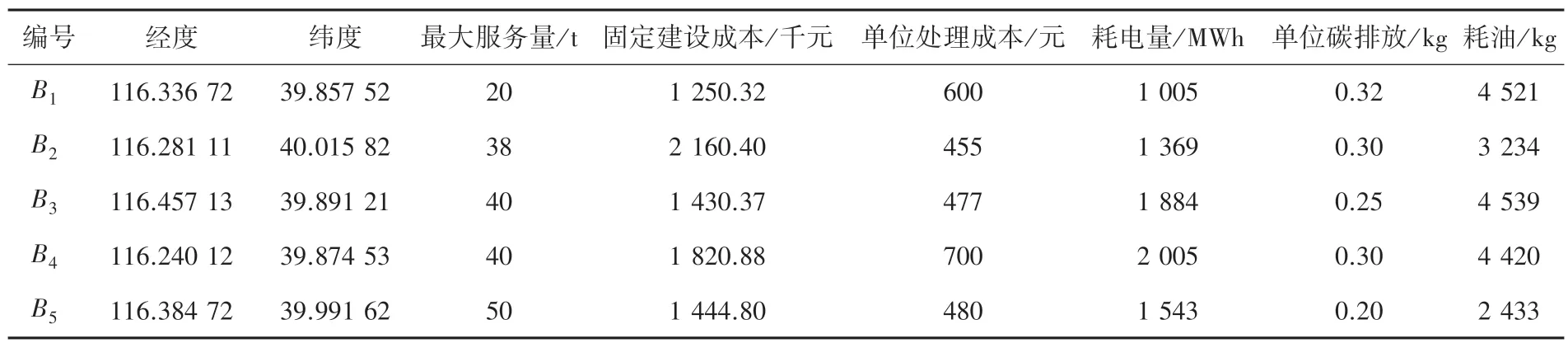
表4 备选配送中心相关信息Tab.4 Information about alternative distribution centers

表5 需求点相关信息Tab.5 Information about demand points
本文以欧氏距离为使用距离,相关公式参考文献[9]。已知,K 公司单位药品运费为10.2 元/(kg·km),表6 为各点之间距离,表7 为相关常量取值。

表6 供应商、配送中心和需求点之间的距离Tab.6 Distance between suppliers,distribution centers and demand points
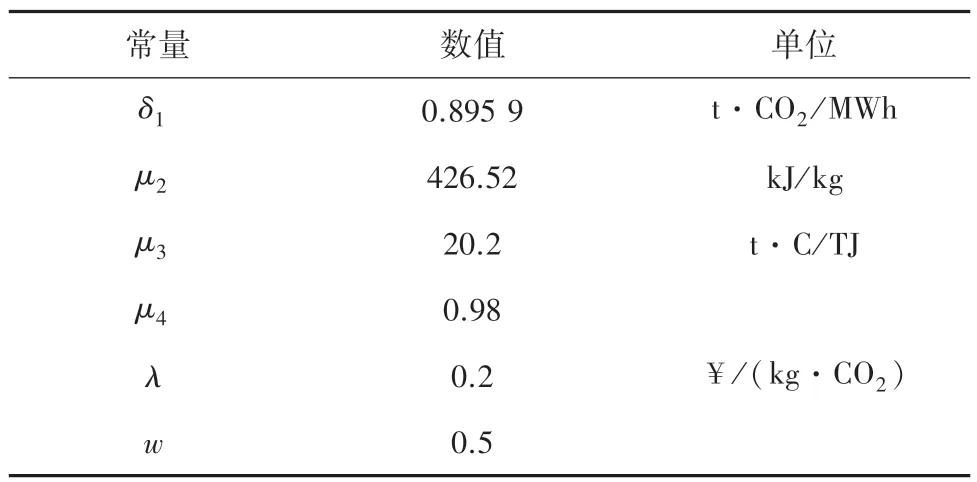
表7 相关常量取值Tab.7 Relevant constant value
3.3 结果分析
将GA 算法、LSO 算法和ILSO 算法进行对比分析。选取式(10)为目标函数,以总成本最小为目标,GA 算法交叉概率设置为0.8,变异概率设置为0.1,种群大小为100;LSO 和ILSO 中成年狮子比例为0.5,种群大小为100。图3、图4 和图5 分别为GA 算法、LSO 算法和ILSO 算法的冷链配送中心选址连接图。

图3 (GA)连接图Fig. 3 (GA)connection diagram

图4 (LSO)连接图Fig. 4 (LSO)connection diagram

图5 (ILSO)连接图Fig. 5 (ILSO)connection diagram
以图5 中ILSO 算法连接图为例进行说明,其中横坐标表示经度,纵坐标表示纬度。红色三角形共有20 个、表示20 个需求点,蓝色正方形共有5 个、表示5 个备选配送中心,红色三角形与蓝色正方形之间的连线,表示某需求点的药品由该配送中心进行配送。文中,ILSO 算法在5 个备选配送中心中选出2 个配送中心为其周边需求点进行配送,分别为1(116.336 72,39.857 52)和 5(116.384 72,39.991 62)。其中,配送中心1 负责需求点1、3、4、6、8、9、10、11、16、19、20 的配送任务;配送中心5 负责需求点2、5、7、12、13、14、15、18、19 的配送任务。
图6 是3 种算法经多次运行,取重复次数最多的迭代效果对比图,表8 是3 种算法运行20 次取平均值的性能比较。GA 算法在迭代196 次左右达到最优值6 252.84 千元,LSO 算法在迭代91 次左右达到最优值6 072.36 千元,ILSO 算法在迭代56 次左右达到最优值5 183.53 千元。ILSO 算法相比LSO算法目标函数降低了14.63%,相比GA 算法目标函数降低了17.11%。因此,ILSO 算法较好地节约了选址成本,而且ILSO 算法在迭代56 次左右达到最优值,LSO 算法在91 次左右达到最优值,GA 算法在196 次左右达到最优值。ILSO 算法相比GA 算法和LSO 算法有更强的收敛能力,求解效率更高。总体而言,ILSO 算法较LSO 算法和GA 算法可以更好地应用于求解配送中心选址问题。
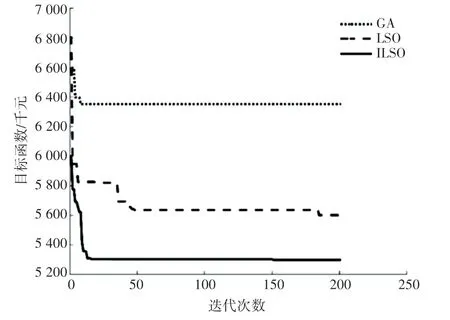
图6 3 种算法迭代效果对比图Fig. 6 Comparison of iterative effect of three algorithms

表8 3 种算法的性能比较Tab.8 Comparison of three algorithms
表9 是在物流服务响应概率为90.14%的情况下,ILSO 算法运行20 次的各子成本平均值。总体可以分为3 部分,即配送中心产生的成本、配送过程产生的成本和碳排放成本。其中,占比最大的是配送中心产生的成本,占总成本的68.47%;其次,是运输过程产生的成本,占总成本的17.55%;最后,是碳排放成本,占总成本的13.98%。

表9 ILSO 下的各子成本Tab.9 Each sub-cost under ILSO
3.4 敏感度分析
考虑到实际配送中,可能存在因为路况不好或者配送车辆故障等原因,导致药品不能及时送达等情况。基于此,对物流服务响应概率进行敏感度分析,使用ILSO 算法计算物流服务响应概率从80%提高到95%的情况下,总成本变化情况以及传统成本和低碳成本之间的关系。
总成本变化曲线如图7 所示。由图7 可以看出,随着物流服务响应概率的提高,总成本呈现快速增长,以85%和90%为分界点,当时间满足率在80%~85%之间时,直线斜率较小,总成本增长幅度较小;当时间满足率在90%~95%时,直线斜率最大,总成本增长最快。

图7 总成本变化曲线Fig. 7 Curve of total cost change
图8 为随着物流服务响应概率的增加,总成本中各子成本之间的变化情况,其中选址成本加上运输成本为传统配送中心选址成本。根据表10 以物流服务响应概率90%为例,选址成本在总成本中占比最大、为72.21%。运输成本在总成本中的占比为15.29%,碳排放成本在总成本中占比为12.49%。因此,企业在选址决策时,从成本最低角度来看应该重点考虑传统成本。
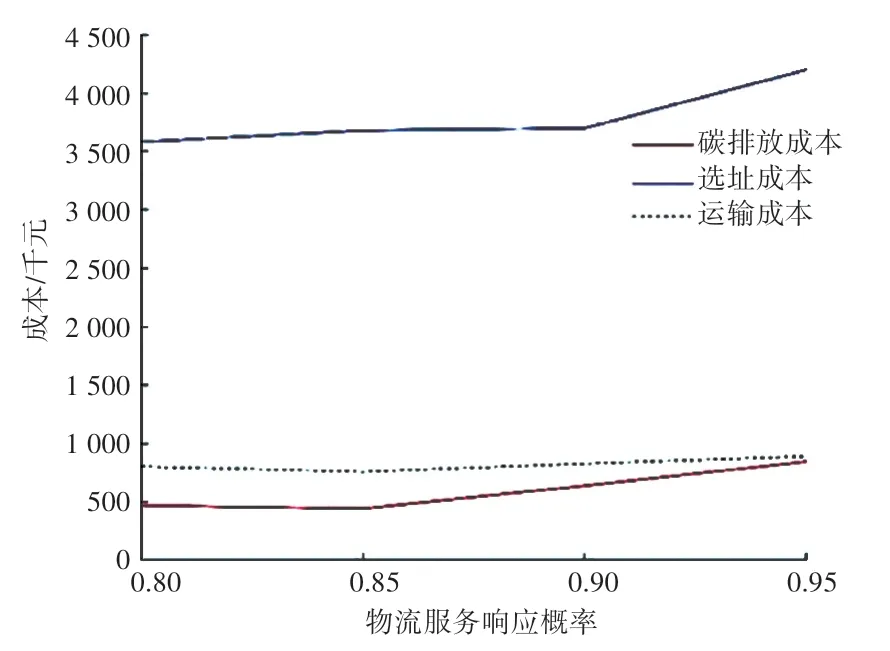
图8 各类子成本变化曲线Fig. 8 Variation curves of various sub-costs
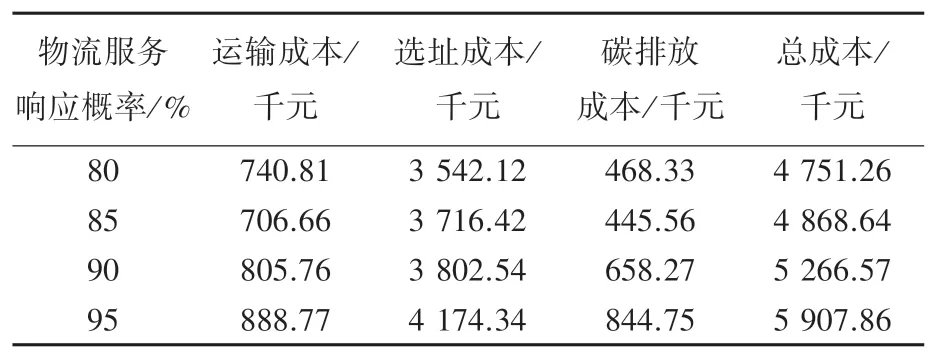
表10 随物流服务响应概率变化的各子成本Tab.10 The sub-costs under different logistics service response probability
碳排放成本变化曲线如图9 所示。由图9 可知,随着物流服务响应概率的提高,碳排放成本并不是直线增加。相反,碳排放成本存在一个先降低、再快速增加的过程。因此,在低碳背景下企业在做选址决策时,选择在哪里建立配送中心以及建立几个配送中心至关重要。但是,对于总成本而言,这一变化影响不大。

图9 碳排放成本变化曲线Fig. 9 Curve of carbon emission cost change
4 结束语
针对配送中实际存在药品可能无法及时送达等情况,提出物流服务响应概率这一概念,并且以物流响应概率为约束条件构建选址模型,在模型中不仅考虑了配送中心产生的碳排放成本,而且还考虑了配送过程中冷链运输车产生的碳排放成本。
在算法改进方面,针对基础狮群算法的局限性。一方面通过引入调节因子,调节狮群中母狮和幼狮的位置转移概率,提高算法随机性。另一方面引入高斯扰动策略,对狮王位置进行多次的变换,加强算法寻优能力。通过对国际通用标准测试函数进行测试表明,本文提出的ILSO 算法相比于LSO 算法和GA 算法具有更强的寻优能力和稳定性。
将ILSO 算法应用于配送中心选址问题,并与LSO 算法和GA 算法进行对比,证明ILSO 算法可以有效降低物流选址总成本,总成本相比LSO 算法减少14.63%,相比GA 算法减少17.11%。其次,通过对物流服务响应概率进行敏感度分析,得出随着物流服务响应概率的增加,碳排放成本呈现出先降低、后快速增加的情况。
