改进麻雀搜索算法求解DFJSP 问题

王 灿，叶春明

（上海理工大学 管理学院，上海 200093）

0 引言

随着经济全球化和制造企业的规模化，分布式制造成为一种常见的生产模式。分布式柔性作业车间调度问题（Distributed flexible job shop scheduling problem，DFJSP）是一个具有重要研究意义的基础性问题，传统的单一工厂集中性生产逐渐被淘汰，多个柔性作业车间相互协同生产调度成为研究的重点。

目前，有关DFJSP研究较少，何怡［1］针对DFJSP 提出一种改进蚁群算法，通过两阶段参数自适应动态调整，并利用旅行商问题验证了算法的有效性，将其应用于DFJSP 的求解。吴锐等人［2］针对DFJSP 特点，设计了三维向量编码，并提出一种改进人工蜂群算法求解。吴秀丽等人［3］提出一种改进差分进化算法求解DFJS 的双目标优化模型，对总成本和提前或延期惩罚同时进行了优化。王彪［4］提出引入自适应移动因子的改进混合蛙跳算法对分布式柔性生产调度进行优化。马庆吉［5］提出一种新的编码方式和基于启发式规则的解码方式，设计了相应的优化策略，并改进灰狼算法求解DFJSP。孟磊磊等人［6］提出一种引入变邻域搜索算法、针对关键工厂全解空间禁忌搜索的混合蛙跳算法。陈文洲等人［7］设计一种基于帕雷托优化方法的人工蜂群算法对低碳DFJS 双目标优化模型进行求解。Giovanni 等人［8］提出一种改进遗传算法求解DFJSP。Lu 等人［9］认为DFJSP 本质是三维解空间探索问题，涉及制造单元分配、机器选择和工序排序三个调度决策，并通过改进遗传算法求解该问题。

麻雀搜索算法（sparrow search algorithm，SSA）是2020 年由薛建凯［10］根据麻雀种群的觅食行为和反捕食行为提出的一种新型群体智能优化算法，与其他算法相比，其搜索精度、收敛速度和稳定性等方面极具竞争力，已被应用于多个领域，目前已然应用于解决车间调度问题。刘丽娜等人［11］提出一种量子计算、正余弦搜索和警戒者数量递减策略改进的麻雀搜索算法，并引入多邻域搜索和高斯扰动策略来求解作业车间调度问题。因此，本文提出一种改进麻雀搜索算法（improved sparrow search algorithm，ISSA），并验证其在求解分布式柔性作业车间调度问题中的有效性。

1 分布式柔性作业车间调度问题

1.1 符号定义

为方便理解，对本文出现的相关符号进行定义，具体含义见表1。

表1 符号定义Tab.1 Symbols definition

1.2 问题描述

DFJSP 包含工序排序、工厂选择、机器选择三个子问题［12］，实质是一个典型的组合优化问题［1］，可将其描述为：将n个工件在f家工厂加工，每家工厂有mr台机器，一个工件的所有工序只能在一家工厂加工，每道工序的可选择加工机器以及加工时间已知。DFJSP 满足以下假设：

（1）所有机器从0 时刻开始可用。

（2）各工件加工的优先级相同，同一工件各道工序有先后约束。

（3）每道工序在同一时刻只能被一台机器加工。

（4）所有工件在0 时刻可以被加工且不考虑工件的运输时间。

（5）机器加工过程中没有故障。

调度的目的是安排每家工厂的每台机器上工件的加工顺序，为每一个工件选择合适的工厂，为每一道工序选择适当的机器，使完工时间达到最小。

1.3 模型建立

本文以最小化全局最大完工时间Cmax为目标进行优化。具体数学模型如下［13］：

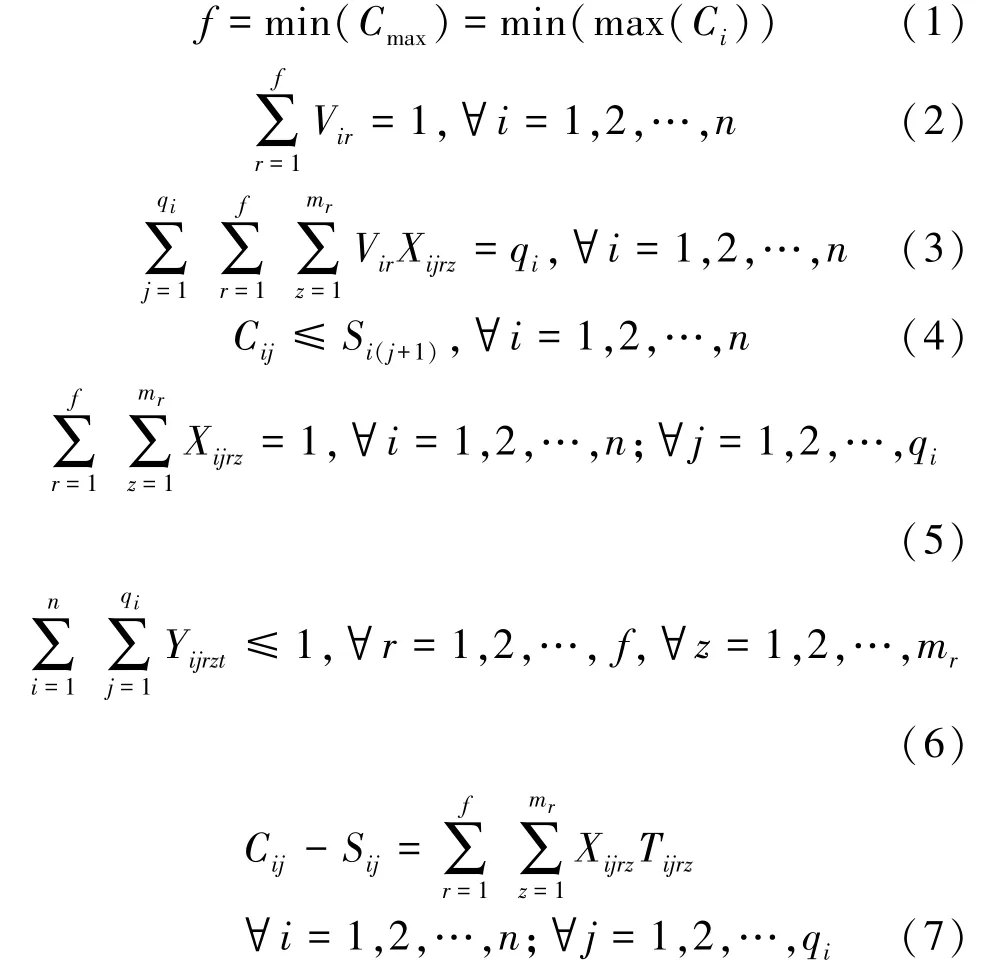
其中，式（1）为目标函数，表示全局最大完工时间的最小化；式（2）表示每个工件只能被分到一家工厂；式（3）表示每个工件的所有工序须在一家工厂完成加工；式（4）表示各工件的工序加工有先后约束；式（5）表示各工序只能选择在一家工厂的一台机器上加工；式（6）表示一台机器在任意时间节点只能对一道工序进行加工；式（7）表示每道工序直到加工完成不会被中断。

2 改进麻雀搜索算法求解DFJSP

2.1 SSA 概述

麻雀搜索算法模拟了麻雀群体的觅食和反捕食行为，在搜索精度、收敛速度和稳定性等方面有较强的竞争力。麻雀个体分为发现者、加入者和侦察者，发现者负责搜寻并为麻雀种群提供食物丰富的区域和方向，加入者跟随发现者以获得食物。此外，种群中存在一定比例的个体负责侦查预警，如发现危险则发出报警信号并在种群中移动，当预警值大于安全值时，发现者需带领加入者移动到其他安全的区域寻找食物。研究对此拟做阐释分述如下。

（1）发现者。每次迭代过程中，发现者位置更新如下：

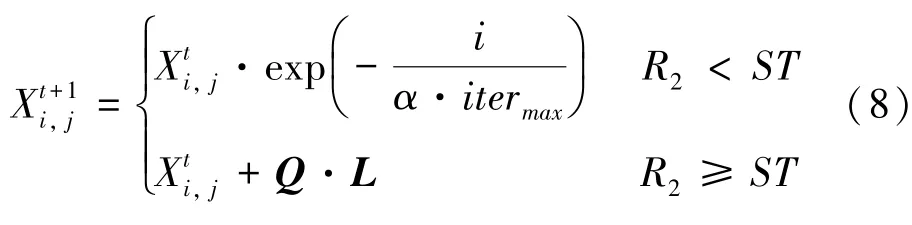
其中，t表示当前迭代次数，j ＝1，2，…，d；itermax表示最大迭代次数；Xi，j表示第i个麻雀在第j维中的位置信息；α∈（0，1］ 表示一个随机数；R2（R2∈［0，1］）表示预警值；ST（ST∈［0.5，1］）表示安全值；Q是服从正态分布的随机数；L表示一个1× d的矩阵且元素全部为1。

（2）加入者。加入者位置更新如下：

其中，Xp表示当前发现者占据的最优位置；Xworst表示当前全局最差的位置；A表示一个1×d的矩阵，元素随机取值为1或-1，且A＋＝ AT(AAT)-1。

（3）侦查者。侦查者位置更新如下：

其中，Xbest是当前全局最优位置；β是服从标准正态分布的随机数；K∈[-1，1]，fi表示当前麻雀个体适应度值；fg表示当前种群中最佳适应度值；fw表示当前种群中最差适应度值；ε为极小的常数。

2.2 编码与解码

本文选用基于工序序列的编码，编码仅包含一条工序序列，序列长度等于所有工件的工序数之和，用来确定工序排序。

麻雀搜索算法用于处理连续型问题，无法直接应用于车间调度等离散型问题，因此需要选择合适的编码方式。n个工件共D道工序，个体位置向量为X ＝［x1，x2，…，xd，…，xD］，各元素可在［-δ，δ］ 中任意取值，并按一定顺序存储。假设有3 个工件、共8 道工序，各元素在［-2，2］ 中任意取值，个体位置向量如图1 所示。

图1 个体位置向量Fig. 1 Individual position vector

采用文献［14］中的转换方法实现连续个体位置向量向离散车间调度之间的转化。转换结果如图2 所示，可得工序序列为O31→O11→O21→O32→O22→O12→O13→O33。

图2 调度方案Fig. 2 Scheduling scheme

与一般车间调度问题相比，DFJSP 需考虑工厂选择，本文工厂选择采用文献［15］的方法，包含3个步骤：

（1）选择每个工件的第一道工序，并维持这些工序的序列，推导得出一个工件序列，如从O31→O11→O21→O32→O22→O12→O13→O33之中选出O31→O11→O21，进而推出工件序列J3→J1→J2。

（2）计算各工件在各工厂的平均加工时间，将工件-工厂-机器表缩减得到工件-工厂表。

（3）按照工件序列，根据当前最大完工时间最小化规则将工件分配给特定工厂。

2.3 种群初始化

SSA 算法随机初始化产生种群个体的方式，会导致生成种群分布不均匀，种群多样性减少，影响算法寻优效率。为保证求解速度和质量，本文初始化种群的生成策略为随机生成与反向学习相混合，50%个体采用随机生成方式，50%个体采用反向学习生成方式。利用反向学习策略［16］生成种群的主要思想：首先随机生成初始种群，再根据初始种群生成其反向种群，从中选择较优的种群作为下一代种群。操作步骤为：

（1）随机初始化n个麻雀个体的位置X ＝［x1，x2，…，xd，…，xD］ 作为初始种群P1，其中各元素可在［-δ，δ］ 中任意取值。

（2）生成初始种群P1中每个麻雀个体的反向个体，构成反向种群P2，其中反向个体位置X' ＝其中。

（3）将种群P1、P2合并，根据适应度值对2n个麻雀个体升序排序，最终选取适应度值前n个麻雀个体为初始种群。

2.4 莱维飞行优化发现者位置

麻雀在觅食状态下的运动路线是莱维飞行轨迹，特点是大范围的探索，折线方式的急剧转向，目标是获得更多食物机会。在SSA 算法中，由于发现者在搜索过程中的带头作用，加入者位置更新易受发现者影响，使得麻雀种群容易出现聚集，陷入局部最优，因此发现者的位置更新必须有一定的随机性。为避免SSA 容易早熟而陷入局部最优，提高全局寻优能力，在发现者位置更新公式中引入莱维飞行［17］。利用Levy 飞行来增加发现者搜索方向的多元性，以增强算法的全局搜索能力，避免陷入局部最优。

Levy 飞行的随机步长s的计算公式为：

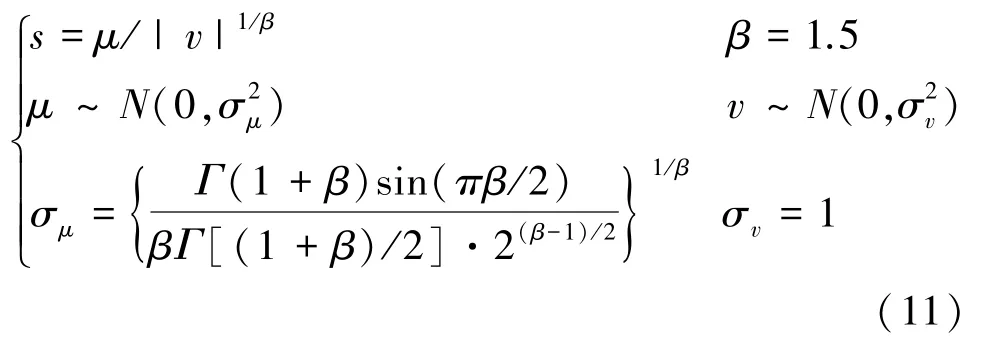
当R2＜ST时，发现者个体位置的每一维都在缩小，因此将发现者位置更新公式改进为：

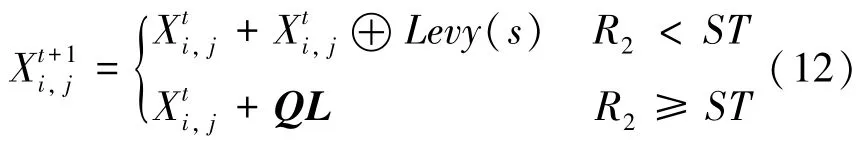
其中，“ ⊕”表示点乘，Levy（λ）表示步长服从Levy 分布的随机搜索向量s（μ，v）。

2.5 学习更新策略优化加入者位置

加入者在有效控制全局探索和局部开发的平衡中发挥重要作用，但发现最优解后，加入者迅速向最优解靠拢，容易陷入局部最优，因此，对加入者的位置引入学习更新策略，使加入者不仅向最优麻雀个体学习，也进行自我学习和随机个体学习。

（1）自我学习。在加入者位置中引入自适应惯性权重因子ω来提升加入者对自身的学习，权重因子ω计算公式如下：

迭代前期，权重因子ω值较大，可提高全局搜索能力，迭代后期ω值自适应减小，有利于进行局部搜索，并提高收敛速度。

（2）最优个体学习。借鉴萤火虫算法［18］中的吸引度规则，萤火虫种群中发光弱的会被发光强的吸引并向其移动，且吸引度仅仅与发光强度、距离相关，距离越大，吸引度越小。吸引度β计算方式如下：

其中，β0表示最大吸引度，即r ＝0 时的吸引度；γ表示光吸收系数，在［0.1，10］ 中任意取值；r表示2 只萤火虫之间的距离；β0＝1。

（3）随机个体学习。向随机个体学习有助于提升种群多样性，但随机个体影响因子过大不利于算法收敛，因此，随机个体学习因子S定义为：

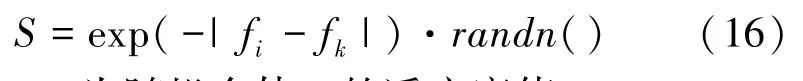
其中，fk为随机个体k的适应度值。

加入者位置更新公式改进为：

其中，Xk，j表示随机个体k的位置。

2.6 正态云模型优化侦查者位置

为进一步提高SSA 跳出局部最优的能力，且提升算法的收敛速度和求解精度，在侦查者位置更新公式中引入云模型［19］。云模型是处理定性概念和定量描述间的不确定转换模型，反映了随机性和模糊性［20］。云的数字特征为期望（Ex）、熵（En）和超熵。期望是能够代表定性概念量化的最典型样本，熵反映了云滴的离散程度和取值范围，超熵反映了云滴的凝聚程度。正态云滴生成过程可定义如下：

其中，Nd表示期望生成的云滴数目。

将当前全局最优位置作为正态云模型的期望Ex，侦查者位置更新公式改进为：

其中，P表示麻雀种群中侦查者的位置；En表示侦查者距离麻雀最优个体的范围；He表示侦查者位置的分散程度。在迭代前期，En值较大，能够提高全局搜索能力，在迭代后期自适应减小，有利于进行局部搜索，提高收敛速度。因此，En，He计算方式如下：

其中，DISPmax表示侦查者距离全局最优位置的最大距离，φ、δ为正整数。

2.7 交叉和变异算子

交叉和变异两个操作相互配合、相互竞争，能够均衡算法的全局搜索和局部搜索能力。考虑到算法的运行时间，本文对每次迭代发现者中任2 个麻雀个体进行交叉操作，因个体位置为连续型向量，故本文设计了一种交叉策略。对每次迭代发现者中任一个麻雀个体进行变异操作，变异算子采用SIM 算子。

交叉策略如图3 所示。首先，在父代中随机选择几个位置可不连续的基因，2 条染色体选择位置相同；然后，将父代1 中所选基因复制到相同位置的子代1 中，并将父代2 中所选基因复制到相同位置的子代2 中；接着，将父代1 中的剩余基因复制到子代2 的同一位置，并将父代2 中的剩余基因复制到子代1 的同一位置。

图3 交叉示意图Fig. 3 Schematic diagram of crossing

变异算子采用SIM 算子，即反转突变，如图4 所示。在麻雀个体中选择一个随机的基因序列，将该序列中的基因顺序颠倒。

图4 变异示意图Fig. 4 Schematic diagram of mutation

2.8 改进麻雀搜索算法步骤

至此，本文改进麻雀搜索算法流程如图5 所示。

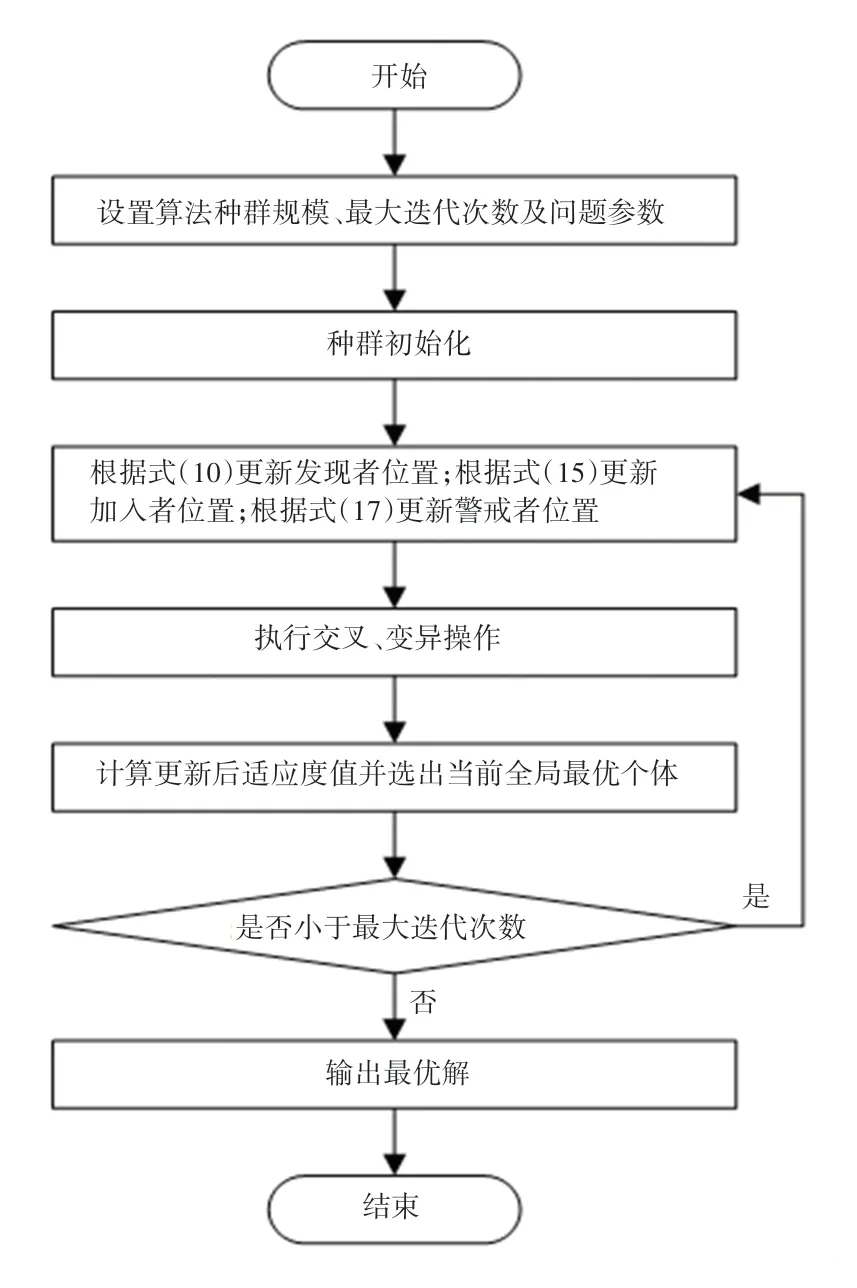
图5 ISSA 算法流程Fig. 5 Algorithm process of ISSA

3 仿真实验与分析

3.1 算例生成

本文使用Fisher 等人［21］设计的3 个典型问题mt06、mt10 和mt20 以及15 个Lawrence［22］基准测试例子la01～la15，并假设所有工厂完全相同，分别考虑2 家、3 家工厂的情况。

3.2 实验结果及分析

为验证ISSA 算法求解分布式柔性作业车间调度的有效性，与SSA 算法、PSO 算法对比进行研究分析。

本文算法运行环境为：Windows10 64 位操作系统，Intel（R）Core（TM）i5-1135G7 ＠ 2.40 GHz 2.42 GHz处理器，16.0 GB 内存，Matlab R2017a 开发软件。

为避免测试结果的随机性，更加准确地对ISSA、SSA、PSO 算法就DFJSP 进行比较，设置每个算法最大迭代次数为500 次，种群规模为100，针对每个算例，每种算法独立运行20 次，取运行结果的最小值和平均值，2 家工厂、3 家工厂实验结果分别见表2、表3。

表2 2 家工厂测试结果Tab.2 2 FMU test results

由表2、表3 结果可知，在最小值方面，ISSA 优于SSA，大部分优于PSO；在平均值方面，ISSA 绝大部分优于SSA 和PSO。综上，ISSA 在多工厂大部分算例上均表现优异，整体寻优性能优于SSA 和PSO。

为更好地对比3 种算法的收敛效果，选取具有代表性的实例mt10、la05、la10、la15，分别绘制了2家工厂、3 家工厂的研究中各算法的收敛曲线对比图，如图6、图7 所示。

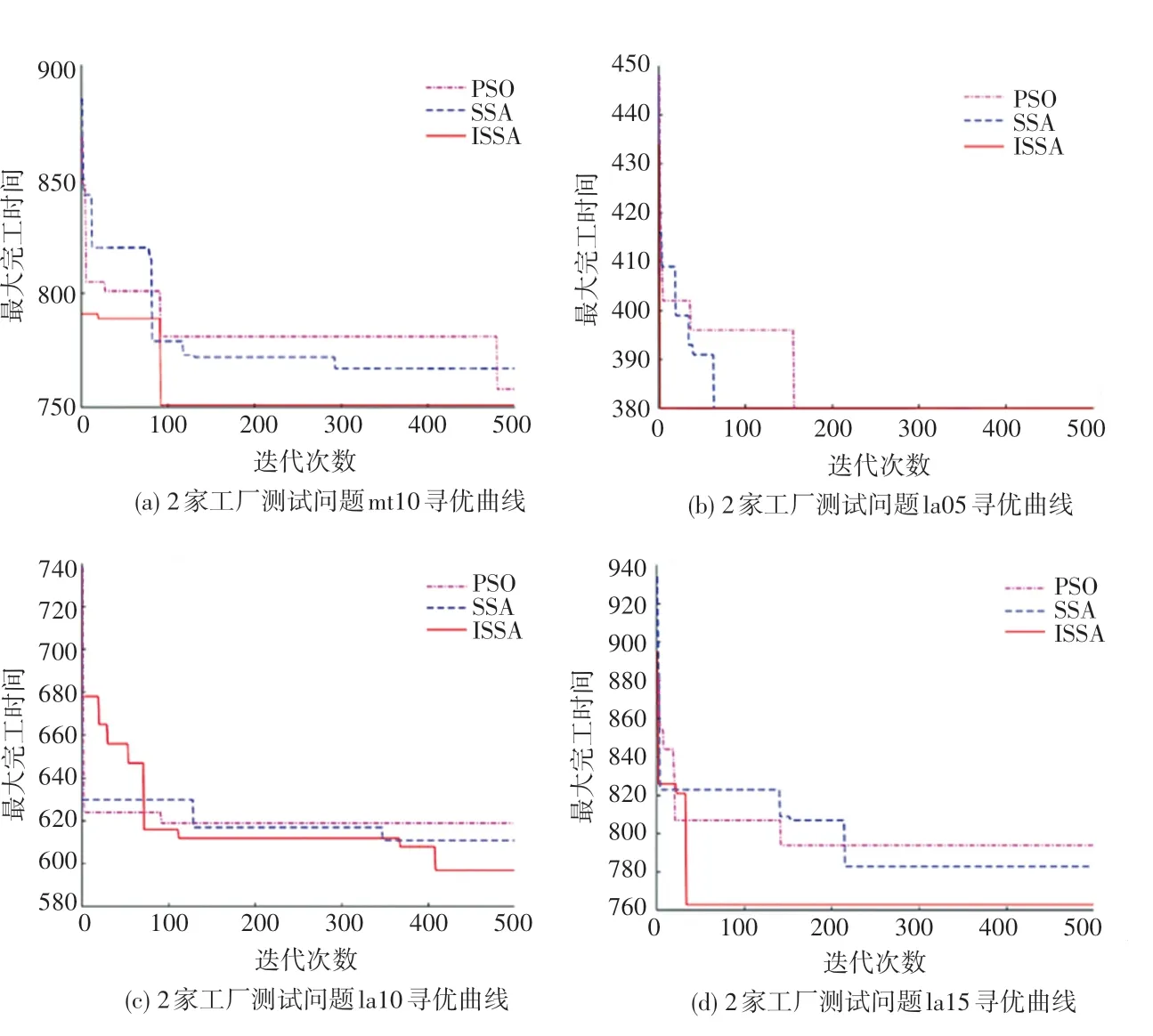
图6 2 家工厂不同算法寻优曲线对比Fig. 6 Comparison of optimization curves of different algorithms for two factories

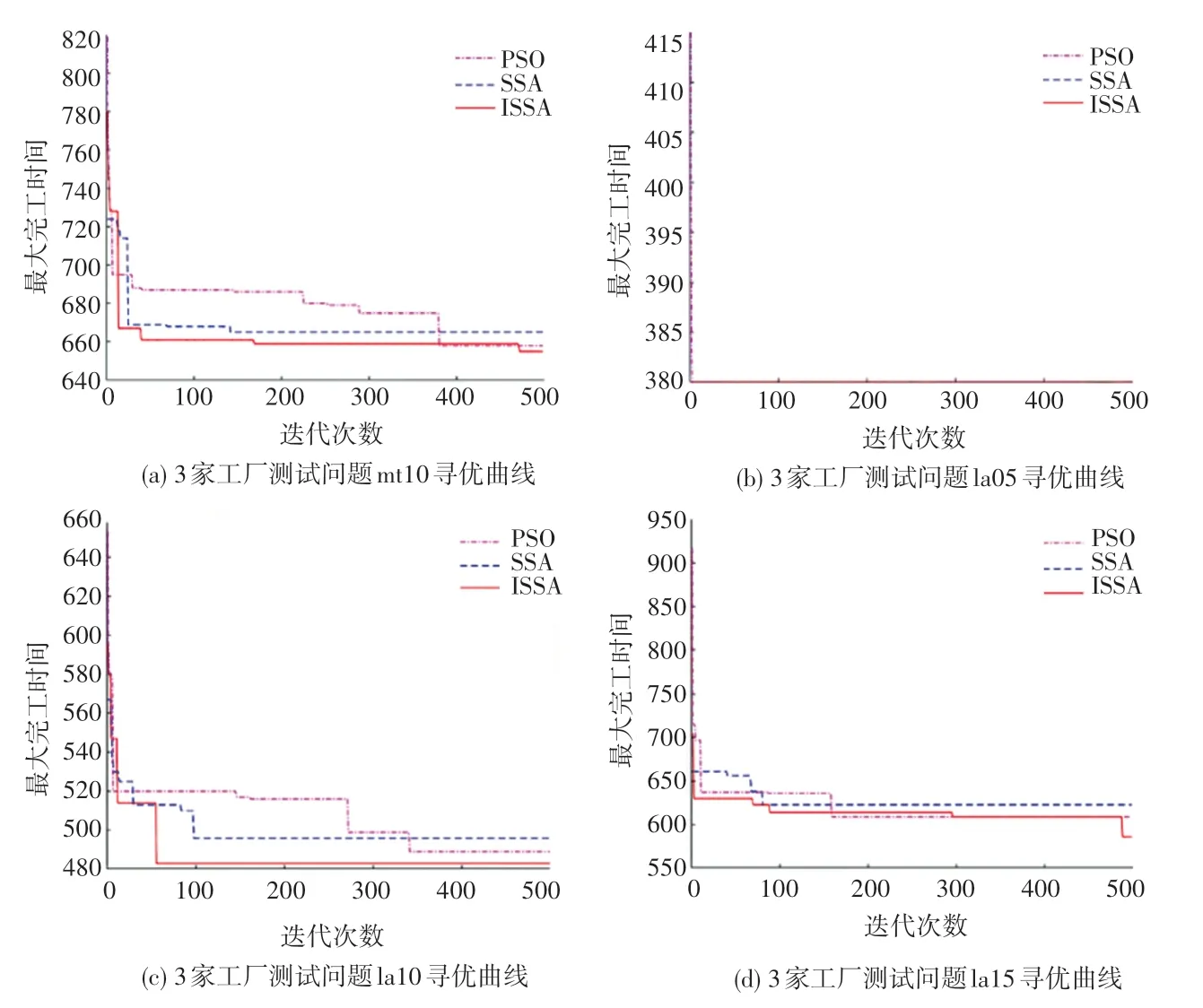
图7 3 家工厂不同算法寻优曲线对比Fig. 7 Comparison of optimization curves of different algorithms for three factories

由图6、图7 中ISSA 与SSA、PSO 算法寻优曲线对比可以看出，在求解2 家工厂、3 家工厂mt10、la05、la10、la15 测试问题时，ISSA 寻优曲线基本位于SSA、PSO 寻优曲线左下方，且除2 家工厂la10、3家工厂mt10、la15 测试问题外，其余测试问题寻优曲线ISSA 均在100 次迭代内居于领先位置，说明ISSA 在求解DFJSP 时的收敛精度和收敛速度优于SSA 和PSO。此外，2 家工厂la10、3 家工厂mt10、la15 测试问题在迭代进行100 次后虽没能持续保持领先，但ISSA 能够在迭代后期跳出局部最优，找到更优解。综上可知，利用莱维飞行、学习更新策略、正态云模型、交叉变异等对经典麻雀搜索算法改进后，ISSA 能够有效平衡全局搜索和局部开发，在求解DFJSP 过程中具有更高的收敛精度和更快的收敛速度。实验利用ISSA 对DFJSP 求解得到的最好调度结果的部分加工甘特图如图8 所示。

图8 部分算例甘特图Fig. 8 Partial examples Gantt chart

4 结束语

本文研究了具有较高复杂度和求解难度的DFJSP，针对其特性，建立了以最小化最大完工时间为优化目标的调度模型。为了有效求解该模型，结合反向学习策略、莱维飞行、学习更新策略、正态云模型及交叉变异算子，提出了一种改进麻雀搜索算法（ISSA），有效避免了SSA 求解时易陷入局部最优的缺点。通过仿真实验与其他算法进行对比，分析验证了ISSA 的性能，表明所提算法能有效求解DFJSP，且具有一定的优越性。目前，DFJSP 的相关研究还有所欠缺，在未来工作中，将进一步改进麻雀搜索算法或利用其他算法及其改进算法来求解该问题，并探索研究更加符合生产实际的多目标DFJSP。