大跨度铁路悬索桥变形验算中的列车荷载折减系数
2022-02-07王兴超李文杰
王兴超 李文杰
1.大连理工大学 建设工程学部,辽宁 大连 116024;2.中国交通建设集团有限公司,北京 100088
中国已经建造了多座多线铁路大跨度桥梁[1],在这些桥梁的设计中遇到了诸多不同于中小跨度铁路桥梁设计的新问题。多线大跨度桥梁承载力设计和变形验算中列车荷载的组合问题即其中之一。这些问题除与大跨度桥梁(斜拉桥、悬索桥或其他组合形式的桥梁)的结构形式有关外,主要与列车荷载模式及列车荷载的概率特性有关。许多学者对大跨度桥梁的挠度特征进行了研究,但是没有深入研究其荷载组合[2-6]。
对于中小跨度铁路桥梁,现行铁路桥梁设计规范均假定列车荷载满布于整个桥梁,并且考虑列车同时出现在桥梁上的概率较小而对列车荷载进行折减。如,中国TB 10002—2017《铁路桥涵设计规范》规定,采用ZK(客车)或ZC(城际轨道交通)活载时,双线桥梁结构按两条线路在最不利位置承受100%的ZK 或ZC活载计算;多于两线的桥梁结构按以下两种情况最不利者考虑:两条线路在最不利位置承受100%的ZK或ZC 活载,其余线路不承受列车荷载;或所有线路在最不利位置承受75%的ZK 或ZC 活载。欧洲规范EN 1991⁃2Eurocode1:Actions on Structures -Part2:Traffic Loads on Bridges和国际铁路联盟规范UIC 776⁃1Loads to be Considered in Railway Bridge Design规定,对于双线桥梁,LM71(正常轨道交通)荷载施加到一条或两条轨道上,取最不利效应;对于三线或三线以上的桥梁,荷载施加到一条或两条轨道上,或者在三条或多条轨道上施加0.75LM71,取最不利效应。美国铁路工程和养护协会标准AREMA 2010Manual for Railway Engineering规定,对于双线桥梁,在双线上均施加全部活载;对于三线桥梁,在双线上施加全部活载,第三线上施加1/2 活载;对于四线桥,在双线上施加全部活载,第三线上施加1/2 活载,第四线上施加1/4 活载;对于四线以上桥梁,由工程师决定加载方式;活载的布置方式应能够使结构产生最大活载应力。大跨度铁路桥梁的长度一般比列车长度大得多,需要按列车可能达到的最大长度合理确定相应的列车荷载。因此,设计大跨度铁路桥梁时,其列车荷载的折减除应考虑列车同时在桥梁上出现的概率外,还应考虑同时使桥梁构件达到最大内力的概率。文献[7]以五峰山公铁两用悬索桥为对象,针对承载能力极限状态设计的列车荷载折减系数进行了研究,表明大跨度桥梁的列车荷载折减系数取值小于规范中针对中小桥梁规定的列车荷载折减系数。
进一步计算表明,在验算列车静活荷载作用下大跨度铁路桥梁的挠度时,采用规范规定的多线大跨度铁路桥梁列车的折减方法或折减系数或取文献[7]针对大跨度铁路桥梁分析得到的列车荷载折减系数,按折减后的列车荷载计算所得挠度不能满足要求。实际上,规范规定的列车荷载折减方法或折减系数是针对承载能力极限状态的,而桥梁的挠度验算属于正常使用极限状态设计。铁路桥梁承载能力极限状态针对结构安全,而正常使用极限状态只是针对影响列车行驶平稳性的结构变形等,并不涉及结构的安全性。因此,对大跨度桥梁变形验算和承载力设计采用相同的列车荷载折减方法或折减系数是不合适的。目前针对大跨度铁路桥梁变形验算中列车荷载折减方法或折减系数的研究很少[8-10]。因此,本文以一座铁路悬索桥为研究对象,通过随机模拟对多线大跨度桥梁挠度验算中列车荷载的折减方法进行研究。
1 工程概况及有限元模型
某铁路大桥为钢桁梁悬索桥,跨径布置为(84+84 +1 092+84+84)m,见图1。大桥下层为四线客运专线铁路(见图2),根据TB/T 3466—2016《铁路列车荷载图示》及文献[7,11]的建议,列车设计荷载为ZK 活载,设计速度250 km/h,设计列车荷载加载长度为550 m,桥面宽度为30 m。列车荷载布置见图3。
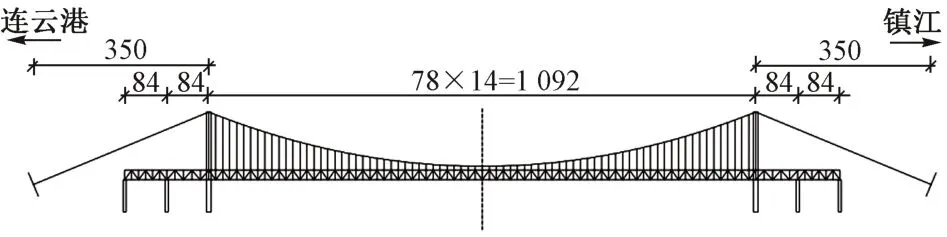
图1 铁路大桥立面布置(单位:m)

图2 桥上铁路线及列车编号
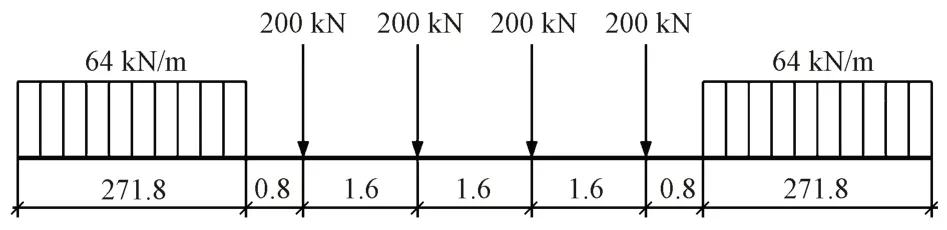
图3 列车荷载布置(尺寸单位:m)
主缆由多股平行钢丝成品索组成,采用高强度锌铝钢丝,强度等级为1 860 MPa,中跨和边跨成桥线形均为二次抛物线。全桥共154 根吊索,采用PPWS 高强度镀锌平行钢丝索,每根吊索有337丝直径5 mm 的平行钢丝编排而成,强度等级为1 770 MPa。钢桁架加劲梁由主桁、铁路桥面系、公路桥面系与横联组成。主结构钢材采用Q370q⁃E,辅助结构钢材采用Q345q⁃D。主梁为板桁结合钢桁架,主桁间距为30 m,桁高16 m,节间长度14 m。铁路桥面系采用纵横梁体系的正交异性钢桥面板,每14 m 设置一道横梁。公路桥面系采用密横梁体系正交异性钢桥面板结构,桥面板厚16 mm,下设U 形加劲肋。主塔为钢筋混凝土框架结构,分别由上、中、下塔柱,上、下横梁及塔顶鞍罩房等部分组成,分南主塔和北主塔。南主塔塔高179.5 m,桥塔横桥向为门式框架结构;北主塔塔高191.5 m,桥塔横桥向为门式框架结构。
为计算列车荷载下桥梁的竖向变形,建立桥梁有限元模型。模型单元包括索单元、梁单元等,加劲梁和主塔要承受轴向拉压、弯曲和扭转作用,选用梁单元进行模拟,共计26 779 个单元。主缆和吊索只能承受拉力,不能受弯、受扭、受压,而且成桥过程中需设定初拉力,采用索单元进行模拟,共计410个单元。模型采用的边界条件为:主塔和桥墩与地基固结;主塔与加劲梁通过支座连接,加劲梁可以产生竖向位移,加劲梁的竖向位移、横向位移与主塔一致;主缆和索鞍之间采用刚性连接,相对位移为0;吊索与加劲梁采用刚性连接;主缆端部完全固结。桥梁构件的材料特性见表1。
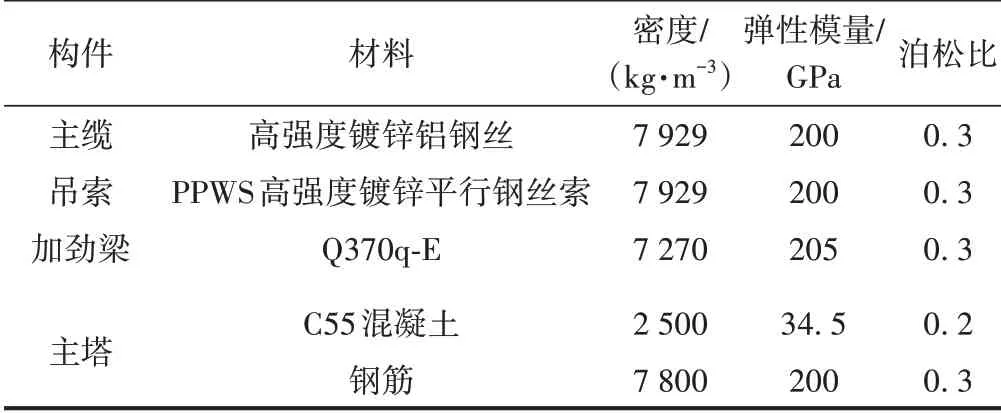
表1 材料物理和力学特性
2 列车荷载下主梁挠度历程曲线
大跨度桥梁设计时,可将所有线路上的列车布置于使桥梁产生最大挠度的位置,计算桥梁的最大挠度,这时只需进行一次有限元分析。但采用随机模拟的方法分析大跨度桥梁某一位置的最大挠度时,根据随机列车在桥梁上位置的不同,要进行多次有限元计算。模拟的次数越多,有限元的计算量越大,需要的时间也越多。如果计算中桥梁整体可以作为一个完全的线弹性体系考虑,则可通过有限元分析建立类似于结构力学中影响线的历程曲线,按照随机模拟的列车在桥梁上的位置,利用历程曲线得到所考虑桥梁位置的挠度。这样不需要每次根据桥梁上列车的随机位置采用有限元方法计算桥梁的挠度,从而使计算大大简化。
大跨度悬索桥为几何非线性结构,理论上主缆的线形与桥梁上的荷载有关。但大跨度悬索桥主要受其自重控制,列车荷载相对于其自重小得多,对桥梁变形影响较小。因此,在计算列车静荷载下桥梁的挠度时,可将其近似视为几何线性结构,即可通过建立的历程曲线确定桥梁某一位置由不同数量的列车、不同位置的列车和不同重量的列车产生的挠度,将这些挠度进行叠加可得到桥梁的总挠度。
每一线路上的列车单独从桥梁的一端行驶到另一端时桥梁上每一位置的最大挠度,见图4(a)—图4(d)。4 列列车同时布置于桥梁时使桥梁不同位置产生的最大挠度见图4(e),桥梁1/4 跨、跨中和3/4 跨处的最大挠度见表2。比较桥上4 条线路上的每一列列车单独行驶时桥梁最大挠度之和与桥上4 条线路上的4 列列车同时行驶时桥梁最大挠度(表3),发现两者非常接近,说明对于大跨度悬索桥,挠度计算中可以忽略几何非线性的影响,用桥梁每条线路上的列车产生的桥梁挠度之和来计算相同行车条件下桥梁相同位置的挠度。

图4 最大挠度的历程曲线
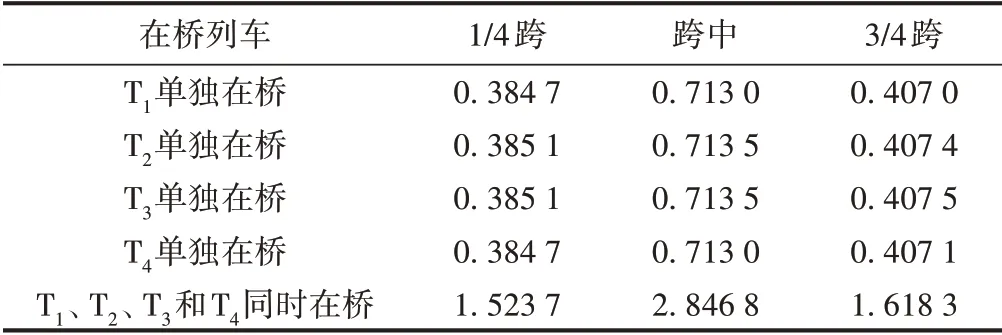
表2 列车荷载下主梁最大挠度 m

表3 两种计算方法挠度比较 m
基于上述分析,使桥梁每一线路上的列车从桥梁的一端行驶到另一端,计算得到桥梁跨中挠度的历程曲线,见图5。可知,当列车行驶到桥梁跨中附近时,桥梁的跨中竖向挠度达到最大,且四条线路上的挠度历程曲线非常接近。因此,为简化计算,在桥梁挠度随机模拟中,采用其中的一条历程曲线或采用四条曲线的平均曲线均可。本文采用四条历程曲线的平均曲线。
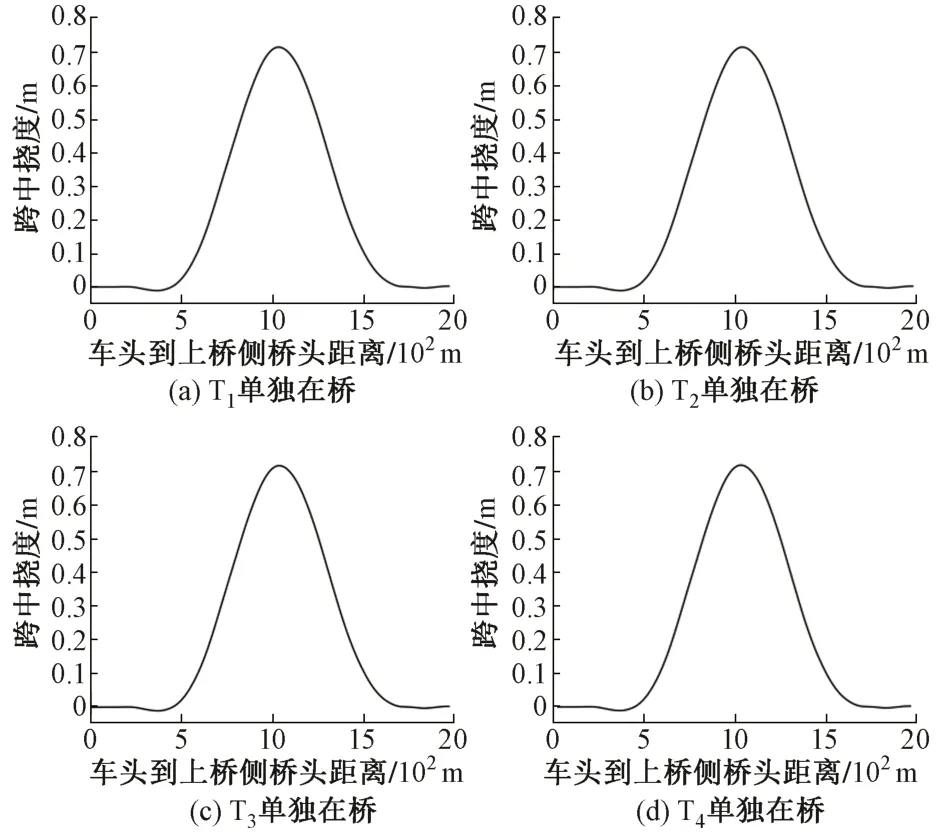
图5 跨中挠度历程曲线
3 列车及列车行驶过程中的随机特征
列车在多线桥梁上行驶,使桥梁产生的竖向挠度值具有非常明显的随机性。这种随机性来源于列车在桥的随机性、在桥位置的随机性和竖向静荷载的随机性。
1)列车在桥的随机性
高速列车运行虽然有严格的时间控制,但受多种因素影响,实际中做到与规定的时间分秒不差是不可能的。另外,在桥梁的设计使用年限内,列车运行时刻表会根据具体情况进行多次调整,所以列车某时刻是否行驶在桥梁上具有较强的不确定性。对于高速列车的控制,我国采用CTCS⁃2 或CTCS⁃3 控制系统,要求同一条线路上列车的时间间隔不小于3 min。根据文献[7],本文将每条铁路线上列车的发车时间作为一个随机因素考虑,假定同线列车发车时间间隔服从平均值为μΔT=3 min、变异系数为δΔT=0.3 的均匀分布,即一条铁路线上的相邻两列列车运行时间间隔服从均匀分布U(td,tu),其概率分布函数为
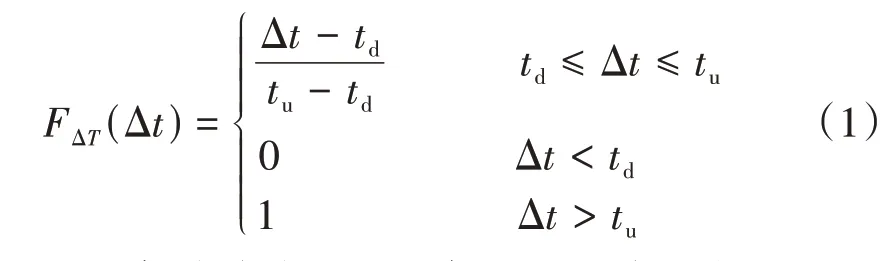
式中:Δt为一条铁路线上的相邻两列列车运行时间间隔;tu、td分别为相邻列车发车时间间隔的上限和下限。tu、td值可按下式确定:
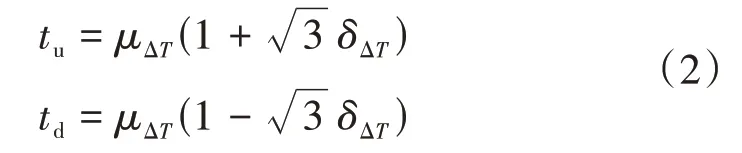
由式(2)得tu=4.56 min,td=1.44 min。由此可见,对本文依托工程而言,理论上不会存在一条线路上有两列列车同时出现在桥上的情况。
桥梁长度比桥梁两端车站间的距离小得多,列车不会总行驶在桥梁上,而是以一定的概率行驶在桥梁上。本文列车速度为v=250 km/h,桥梁总长度L=84 ×4+1 092=1 428 m,列车长度l=550 m,则桥梁的一条线路上有列车行驶的概率为

如果桥梁上有n条线路,则桥梁上同时有k列列车行驶的概率为
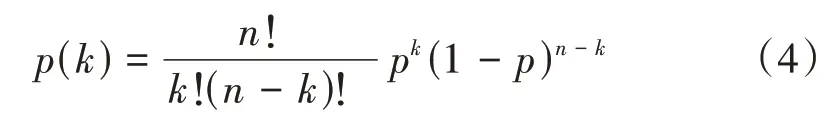
由于桥梁设计关心的是桥梁上有列车行驶的情况,因此本文只分析桥梁上有列车行驶的概率。在桥梁上有列车行驶的条件下,有k列列车的概率为
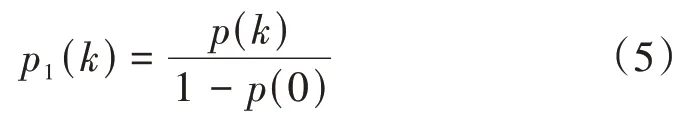
表4 为根据式(5)计算的桥梁上有列车行驶时不同数量列车的概率。以四线桥梁为例,由表4可知,如果桥梁上有列车行驶,是1 列列车的概率较大,为0.758 2;是2 列列车的概率为0.213 7;是3 列列车的概率为0.026 8;是4 列列车的概率为0.001 3。由此可见,在桥梁上有列车行驶的前提下,同时有多列列车的概率很低,这是大跨度桥梁承载力设计和桥梁挠度验算中需对列车荷载进行折减的原因之一。
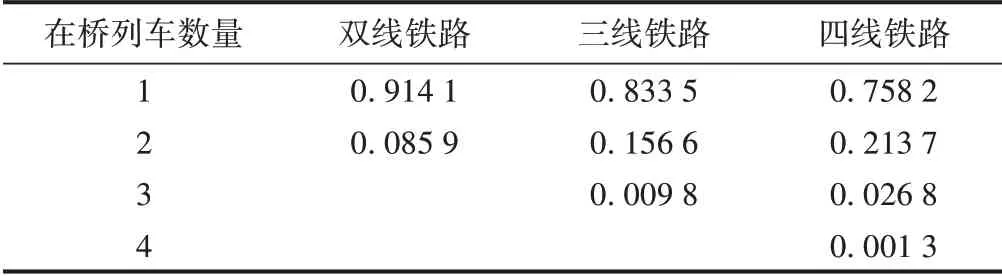
表4 桥梁上有列车行驶的条件下列车同时在桥的概率
2)列车在桥梁上位置的随机性
在同线路上列车发车时间为随机变量的假定下,某时刻列车在桥梁上的位置也是随机性的,其随机特征决定于同线路上列车发车的时间间隔。由于不同线路上的列车在桥梁上行驶时位置是不确定的,这些列车同时出现在使桥梁构件达到最大内力或桥梁跨中最大挠度的概率很小。这是大跨度桥梁构件内力和桥梁挠度计算中需对列车荷载进行折减的另一个原因。
3)列车竖向静荷载的随机性
列车本身的重量及列车上人、物的重量也是不确定的。研究表明[12],列车荷载服从正态分布,均值系数为0.7,变异系数为0.07,概率分布函数为

式中:μQ为列车竖向静荷载的平均值,取为μQ=0.7Qk,Qk为根据图3 所示的列车荷载图式确定的列车荷载标准值;σQ为列车竖向静荷载的标准差,σQ=μQ δQ=0.049Qk。
大跨度悬索桥的竖向刚度较小,列车在桥梁上行驶产生的竖向冲击力很小,根据相关研究可以忽略冲击力的影响。
4 多线大跨度铁路桥梁挠度概率分析
根据列车在桥、在桥位置和列车荷载的概率模型,结合挠度历程曲线,可通过理论推演建立桥梁竖向挠度的概率模型,但推演过程非常复杂,而且涉及多维积分,难以直接用其计算桥梁挠度验算所需的列车荷载折减系数。考虑到采用蒙特卡洛方法可以模拟列车的行驶过程,根据列车行驶在桥梁上的位置,利用挠度历程曲线确定桥梁的挠度,再通过统计分析建立桥梁挠度的概率模型更为直观和简单。本文采用蒙特卡洛方法通过随机模拟研究桥梁挠度的概率特征。
4.1 列车车队随机模拟和桥梁挠度采样
根据式(1)采用蒙特卡洛方法产生多线桥梁每条线路上列车发车时间间隔和距离间隔的随机样本。线路Li列车发车的第j个时间间隔为Δtij;根据x=v⋅Δt可得到每条线路上列车的间距,线路Li上的第j间距为Δxij。根据式(6)采用蒙特卡洛方法产生上述列车的竖向荷载随机样本,线路Li的第j列车的荷载为Δqij。
将生成的随机车队施加在两条铁路线的每条线路上。从某时刻开始计时,每0.1 s 进行一次采样,确定桥梁每条线路上列车的状态,即此刻桥梁每条线路上是否有列车、列车的位置和列车的静荷载。根据这些信息利用挠度历程曲线确定桥梁上每列列车产生的桥梁跨中挠度,将得到的挠度相加即得到此刻桥梁跨中挠度的一个样本,以两条铁路为例,叠加方式见图6。对列车车队模拟24 h,得到864 000 个桥梁跨中挠度。对这些挠度样本进行统计分析,即得到桥梁挠度的概率特性。
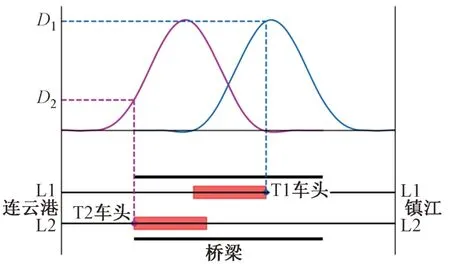
图6 两条铁路线上列车荷载的叠加
4.2 挠度统计分析和列车荷载折减系数
对按上述方法得到的列车静荷载下桥梁跨中挠度样本进行统计,得到桥梁跨中挠度的概率分布。除去桥梁上无列车行驶情况的数据(即挠度为0 的数据),将得到的桥梁跨中挠度样本自小到大排列,并将最小值与最大值的区间等分为若干个子区间,统计每一子区间内跨中挠度样本的数量,从而得到桥梁跨中挠度的概率分布,见图7。
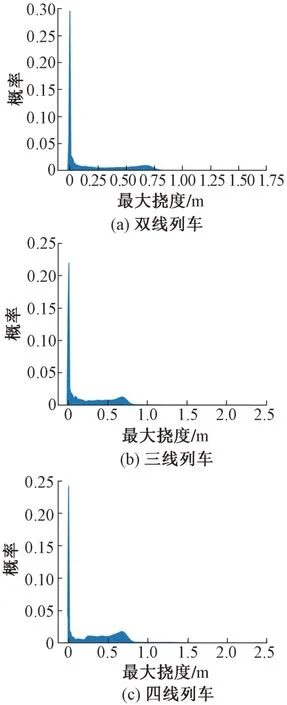
图7 多线列车铁路桥跨中挠度概率分布
针对不同线路的情况,将列车分别布置在使桥梁产生最大挠度的位置,计算得到多线铁路桥梁的最大挠度Dmax。由图7 可知,桥梁跨中挠度概率分布呈现多峰分布,虽然统计分析时已经除去了桥梁上无列车行驶的情况,但大部分情况下列车荷载产生的桥梁跨中竖向挠度接近0,桥梁竖向挠度达到最大挠度(双线、三线和四线分别为1.427、2.140、2.853 m)的概率很小。
桥梁挠度验算属于正常使用极限状态设计的内容。根据GB 50216—2019《铁路工程结构可靠性设计统一标准》的规定,正常使用极限状态设计的荷载组合包括特征组合、频遇组合和准永久值组合。特征组合用于不可逆正常使用极限状态设计,频遇组合用于可逆正常使用极限状态设计,准永久值组合用于长期效应为决定因素的情况。列车在大跨度桥梁上行驶时桥梁产生竖向变形,桥梁变形是可逆的,所以桥梁挠度的验算宜采用频遇组合。可利用本文桥梁挠度的随机模拟结果,确定桥梁列车荷载的频遇值系数。
GB 50216—2019 规定了两种确定正常使用极限状态可变荷载或荷载效应频遇值的方法。其中一种方法是按荷载或荷载效应被超越的总持续时间与设计基准期的比值确定,本文采用此方法。桥梁跨中挠度D(t)的随机过程曲线如图8 所示,在设计时间段T内,桥梁挠度超过某一值Dx的总持续时间为Tx=∑Δti,用Tx与时间段T的比值ηx(称为允许超越时间比)表征频遇值作用效应持续的短暂程度。该标准建议取ηx=0.1,表示如果桥梁的设计使用年限T=100年,桥梁竖向挠度超过规定值Dx的平均时间Tx约为10年。
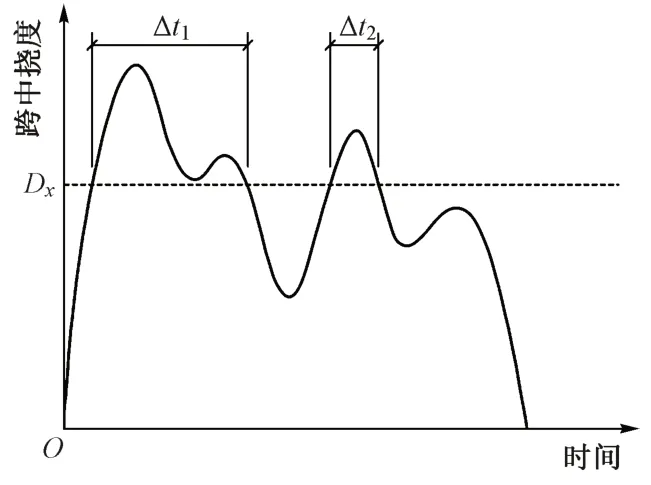
图8 跨中挠度随机过程曲线示意
对桥梁跨中挠度进行了T=24 h 的随机模拟,竖向挠度Dx与总平均时间Tx的关系曲线见图9。以四线为例,按GB 50216—2019,取ηx=0.1,则允许桥梁24 h内超越时间为Tx=0.1T=2.4 h 对应挠度为Dx=0.656 2 m。参考TB 10095—2020《铁路斜拉桥设计规范》的规定,桥梁在列车静活荷载下主梁的挠度不小于其主跨的1/500。大桥的主跨跨度为1 092 m,因此允许的挠度值为Dx=1 092/500=2.184 m。显然,该桥在列车静活荷载下主梁的竖向挠度满足要求。
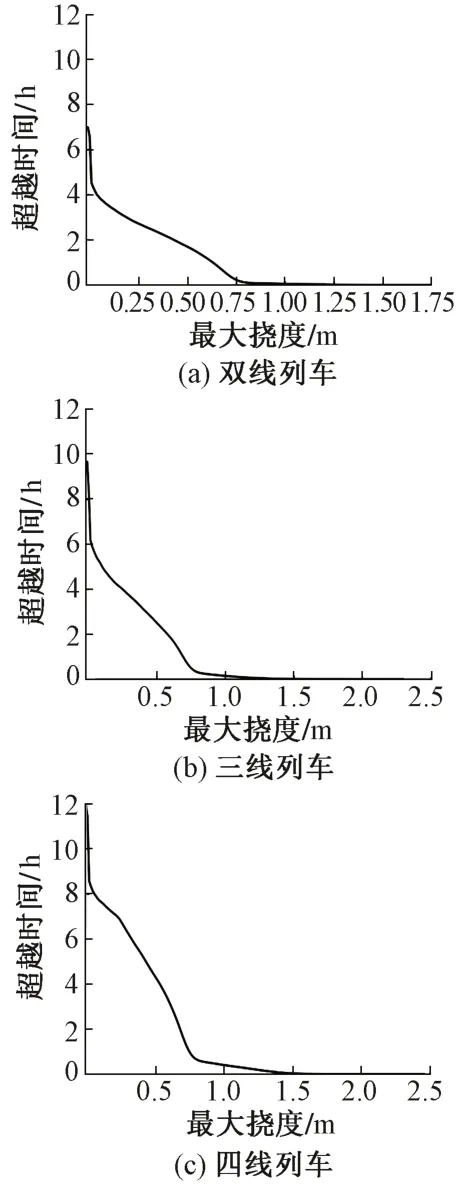
图9 多线铁路主梁竖向挠度超越时间
定义多线大跨度铁路桥梁主梁挠度验算的列车静活荷载折减系数ηD为

在超越时间比ηx=0.1的条件下,双线、三线和四线大跨度铁路桥梁竖向挠度验算时列车静活荷载的折减系数值见表5。可知,不同数量铁路线的折减系数十分接近。随着铁路线数量的增加,Dx和Dmax都有所增加,并且增加幅度相近,这导致折减系数的变化并不显著,折减系数建议值则不发生变化。

表5 主梁竖向挠度折减系数
5 结论
本文以一座铁路悬索桥为研究对象,通过对列车的随机模拟研究了多线大跨度铁路桥梁主梁挠度的概率特征,根据正常使用极限状态设计可变荷载频遇值的概念,确定了多线大跨度桥梁竖向挠度验算的列车静活荷载折减系数。得出以下结论:
1)列车静活荷载下多线大跨度铁路桥梁的挠度验算属于正常使用极限状态设计的内容,竖向挠度验算应按正常使用极限状态的要求确定荷载折减系数。
2)按正常使用极限状态的频遇组合,基于主梁挠度的概率分析,双线、三线和四线大跨度铁路桥梁竖向挠度验算时列车静活荷载的折减系数均可取为0.25。
