基于一维深度卷积生成对抗网络的钢轨波磨识别方法
2022-02-07谢烨赵闻强杨红运包学海
谢烨 赵闻强 杨红运 包学海
1.浙江省交通投资集团有限公司 智慧交通研究分公司,杭州 310016;2.浙江杭海城际铁路有限公司,浙江 海宁 314499
轨道交通列车具有载重量大、运行密度高等特点,频繁的轮轨相互作用会导致钢轨上出现波浪形的磨损,即钢轨波磨。车轮在经过钢轨波磨区域时引发的强烈振动和噪声会大大加快钢轨和轴箱内零件的疲劳损坏速度[1-3]。波磨出现前后驾驶室内噪声波动幅值可达到10 dB 左右,波磨造成的振动还会导致轴向吊耳断裂、钢轨扣件弹条断裂等问题[4-6],大大增加列车运行维护成本。所以,对钢轨波磨进行识别具有十分重要的意义。
由于钢轨发生波磨位置不确定,虽然使用波磨测量仪进行检测具有很高的准确性,但需要投入大量的时间和人工成本。振动监测是一种在线状态监测方法,具有直接、实时的优点,并且设置后无需人工干涉即可对数据进行采集,目前已广泛应用于各种设备的状态监测中[7-8]。将振动监测应用于钢轨波磨监测中,可根据轮轨接触产生的振动直观地观察到振动状态的变化;根据振动特征制定辨识模型,在钢轨波磨的状态监测上更具即时性。目前许多学者基于振动响应对钢轨波磨的状态监测进行了研究。文献[9]对钢轨波磨振动信号进行降噪处理,然后使用希尔伯特-黄变换(Hilbert⁃Huang Transform,HHT)对信号进行时频分析,得到了较为准确的分析结果。文献[10]通过仿真模型得到钢轨波磨振动仿真信号,计算小波包能量熵,实现了较为准确的钢轨波磨检测。文献[11]通过使用时间-能量信息的波磨指数和能量因子,设计了一种双指标联合钢轨波磨评价方法,可以对钢轨波磨的波长和幅值进行评价,并通过实测钢轨波磨信号验证了其方法的准确性。
随着大数据技术的发展与普及,智能状态监测与诊断成了新的研究热点,使用设备的振动信号训练分类模型并对其状态进行分类,已经广泛应用于滚动轴承[12-14]、齿轮箱[15-17]和发动机[18-20]等机械设备的状态监测与故障诊断。已有学者将智能诊断模型引入钢轨波磨的识别研究中。文献[21]对地铁钢轨波磨振动信号进行空间域分割后,使用一维卷积神经网络进行了波磨识别与分类,并使用实测钢轨波磨振动信号进行试验,得到了很高的钢轨波磨识别率。文献[22-23]通过经验模态分解(Empirical Mode Decomposition,EMD),提取包含故障的本征模函数(Intrinsic Modal Functions,IMF)的能量和峭度,将其多尺度能量和峭度特征输入神经网络进行波磨识别。
针对现有研究方法中存在的数据模型与真实钢轨波磨数据有较大偏差,即波磨故障识别准确率较低问题,本文提出一种基于一维深度卷积生成对抗网络的钢轨波磨识别方法。首先使用一维生成对抗网络生成与实际波磨振动信号结构相同的伪样本,对样本信号的数据集进行扩充;然后提取波磨振动信号的时域统计指标作为波磨数据的特征;最后使用分类算法对不同特征的波磨振动数据进行学习与分类,以实现准确地提取实际波磨数据故障特征,识别钢轨波磨故障的目标。
1 生成对抗网络基本原理
生成对抗网络(Generative Adversarial Networks,GAN)是一种生成模型,由Goodfellow在2014年首次提出[24],由生成网络G和判别网络D构成。G通过学习真实样本的结构,生成与真实样本结构相似的伪样本;D用来分辨输入数据是真实样本还是伪样本。G与D通过博弈,彼此不断学习提升。直到D无法判断输入数据是真实样本还是伪样本时,说明G已经学习到真实样本数据结构。
GAN的训练方法如下。
1)高斯噪声通过G生成伪样本,将伪样本和真实样本输入最后一层激活函数为sigmoid 函数的D,真实样本的标签设定为1,伪样本的标签设定为0,转化为一个二分类问题。使G的权值不变,通过反向传播方法更新D中的权值,使D的判断能力提高,用交叉熵作为其损失函数J(D),表达式为
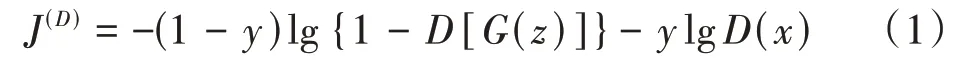
式中:y为样本标签;x为真实样本;G(z)为生成的伪样本,z为输入G的高斯噪声;D(x)和D[G(z)]为真实样本和伪样本通过判别网络的输出。
2)将伪样本输入D,并将伪样本的标签记为1,通过反向传播方法更新G的权值,使D将伪样本判断为真实样本,从而使G可以学习真实样本数据的结构。同样使用交叉熵作为损失函数J(G),表达式为

3)不断进行迭代交替训练。G的目标是生成足够真的伪样本,使得D无法准确判断;D的目标是尽量准确判断真实样本和伪样本。G和D的损失函数可以等价为
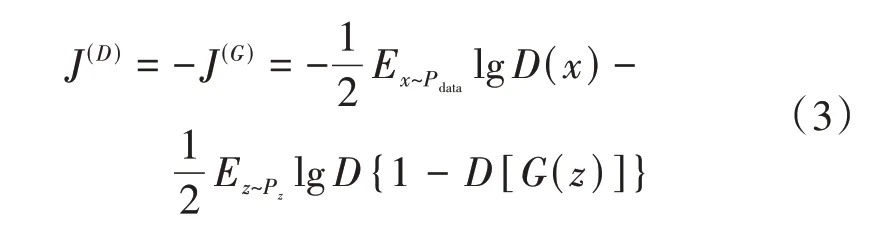
式中:Ex~Pdata为x的熵,Pdata为x的概率分布;Ez~Pz为z的熵,Pz为z的概率分布。
总体损失函数V(D,G)表达式为
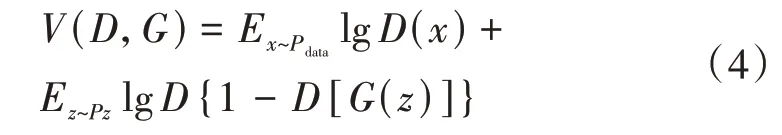
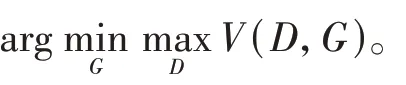
网络训练的最终理想结果是使G和D达到纳什均衡,D无法判别G生成的伪样本是否为真实样本,即D[G(z)]=0.5。深度卷积生成对抗网络(Deep Convolutional Generative Adversarial Networks,DCGAN)是一种基于GAN 的改进算法[25]。该算法是将G和D均设计为卷积神经网络,以卷积神经网络强大的特征提取能力,提高GAN 的效果。基于此,本文使用1D⁃DCGAN 对一维钢轨波磨振动信号进行伪样本生成。
2 基于1D⁃DCGAN 的钢轨波磨识别方法
DCGAN 最初被应用于图像生成。对于一维波磨振动信号,设计合理的1D⁃DCGAN 有助于网络提取波磨振动信号的特征和学习波磨振动数据的结构。基于1D⁃DCGAN 的钢轨波磨识别方法分为以下四个步骤。
1)波磨振动数据预处理;
2)波磨振动数据伪样本生成;
3)波磨振动数据时域特征提取及降维;
4)分类模型的训练与钢轨波磨状态识别。
2.1 波磨振动数据预处理
从实测数据中筛选出质量较好的波磨振动数据,将50%的数据作为1D⁃DCGAN 模型训练数据,剩余50%的数据作为波磨识别测试数据。将训练数据进行归一化处理,然后输入到设计好的1D⁃DCGAN 模型中。
2.2 1D⁃DCGAN的模型结构设计
1D⁃DCGAN 网络参数见表1。模型中,以高斯噪声z作为G的输入,经过反卷积和激活函数输出G(z),将G(z)和x随机输入D,经过多层卷积层计算,输出标签为0或1,其中0代表伪样本,1代表真实样本。为了将输出层得到的伪样本数值限制在[-1,1],使用tanh作为生成网络输出层的激活函数;为了使判别网络的输出值为0 或1,使用sigmoid 作为判别网络的输出层激活函数。在GAN 的训练过程中,由于判别网络和生成网络训练不平衡,容易出现生成网络梯度消失。为减少这一影响,每更新一次判别网络参数,训练四次生成网络。

表1 1D⁃DCGAN网络参数
2.3 时域统计指标的特征提取及降维
对实测钢轨波磨振动数据与1D⁃DCGAN 生成的伪样本进行时域统计指标特征提取,包括均值、均方根值、方根幅值、绝对平均值、偏斜度、峭度、方差、最大值、最小值、波形指标、峰值指标、脉冲指标、裕度指标、偏斜度指标、峭度指标共15种时域特征统计指标。通过主成分分析(Principal Component Analysis,PCA)降维后,前3 个主成分分量的累计贡献率就可以达到95%以上。为了便于特征可视化和减少分类模型的计算量,提取前3 个主成分作为钢轨波磨振动数据的特征。
2.4 分类模型的训练与钢轨波磨状态识别
分别使用K 近邻算法(K⁃Nearest Neighbor,KNN)、支持向量机(Support Vector Machine,SVM)和决策树(Decision Tree,DT)三种不同的分类模型对钢轨波磨特征进行分类。为了模拟不同程度的钢轨波磨状态,将振动信号的幅值A分别缩小50%和增大50%。
在钢轨波磨状态识别过程中,将正常钢轨的标签设定为0,幅值为0.5A、1.0A、1.5A的钢轨波磨数据标签分别设定为1、2、3。将测试数据输入到训练好的分类模型中,对正常钢轨与不同波磨程度的钢轨进行状态识别。
3 试验验证
3.1 数据概况
试验数据选用杭海(杭州—海宁)城际铁路的列车实测轴箱振动信号。杭海城际铁路于2021 年6 月开始进行初期运营,全长46.38 km,全线共12个站点,列车采用DC1500V架空接触网授电的B2型车,2动车 +2 半动车,4 辆编组,运行速度为80 km/h。使用振动采集器对列车轴箱的振动信号进行采集,传感器的布置见图1。采样频率为5 120 Hz,每条数据为1 000 个采样点。对获取的轴箱振动信号进行筛选,共获得400条品质较好的钢轨波磨样本数据。其中200条数据作为训练数据,输入到1D⁃DCGAN 中进行模型训练;剩余200 条数据作为测试样本,用作最后的钢轨波磨识别。

图1 轴箱振动测试中传感器的布置
3.2 数据生成
使用所设计的1D⁃DCGAN 模型进行数据生成。首先将200条真实的钢轨波磨样本数据进行归一化处理,然后输入到模型中进行训练。其中,优化器使用Adam,学习率设置为0.000 01,迭代次数100 万次。为了得到最好的模型,每迭代5 万次对当前模型进行保存,然后继续迭代。迭代完成后,挑选判别器对真实样本和伪样本的判别准确率都在50%左右的模型,这个模型就是当前最优模型。使用binary crossentropy作为损失函数,batch_size 设定为10,padding 选择same。训练完成后,将1D⁃DCGAN 生成的数据进行反归一化,以得到与真实样本相同的幅值。
通过训练好的网络生成伪样本,与真实样本进行对比,见图2。可知:在时域上,伪样本与真实样本的幅值基本一致,且结构表现较为一致;在频域上,伪样本与真实样本均在500 Hz和800 Hz附近幅值较大,二者主要频段基本一致。
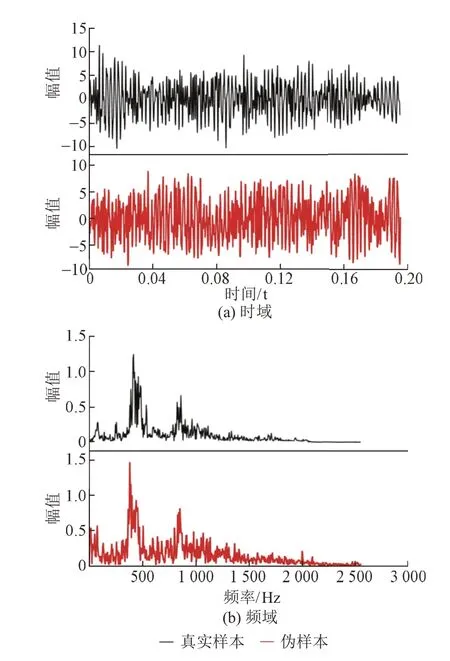
图2 真实样本与伪样本的时频曲线对比
对真实样本、1D⁃DCGAN 生成的伪样本及无损钢轨数据,计算15 个时域特征指标,使用PCA 降维后提取前3 个主成分分量作为其特征,见图3。可知:伪样本与真实样本的特征基本相同,并且与正常钢轨提取的特征区别较大。

图3 真实样本、伪样本与无损钢轨波磨数据特征对比
3.3 数据集的建立
挑选4 000 个正常钢轨的振动信号,作为无波磨故障的振动信号;通过1D⁃DCGAN 生成1 000 个伪样本波磨数据,作为波磨振动信号。为了对不同程度的波磨情况进行模拟,分别将波磨信号的幅值A缩小至0.5A和增大至1.5A,即训练数据包含4 000 个无波磨数据和1 000 个0.5A的波磨数据、1 000 个1.0A的波磨数据和1 000个1.5A的波磨数据。将测试数据中的200 条钢轨波磨数据进行幅值放大、缩小后,与200 条无波磨数据一起作为测试数据集。
3.4 试验结果及分析
计算不同幅值波磨数据的15种时域统计指标,使用PCA 对特征进行降维后,取前3 个主成分分量作为其特征,见图4。可知:波磨信号的幅值越高,波磨振动的信号越大,使用一维深度卷积生成对抗网络的钢轨波磨伪样本与真实波磨样本特征越接近。
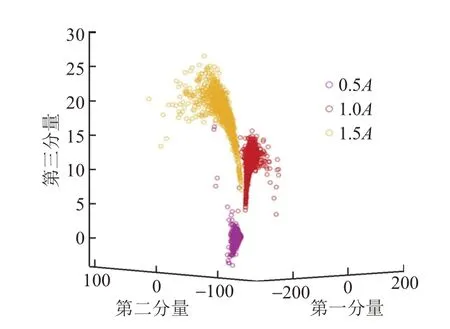
图4 不同幅值波磨数据特征对比
为了表明研究数据量对模型训练以及分类准确率的影响,分别用不同数量的数据进行模型训练,并对比其准确率。使用KNN、SVM 和DT 三种分类模型进行模型训练和分类,训练模型的数据量分别为样本总量的20%、40%、60%、80%和100%,其分类准确率与样本数量的关系见图5。可知:三种分类模型的平均分类准确率都随着训练数据样本数量的增加而增大,其中平均分类准确率最高的是SVM,可以达到96.344%;准确率随数据规模变化最明显的是DT,从89.5%增至92.5%。
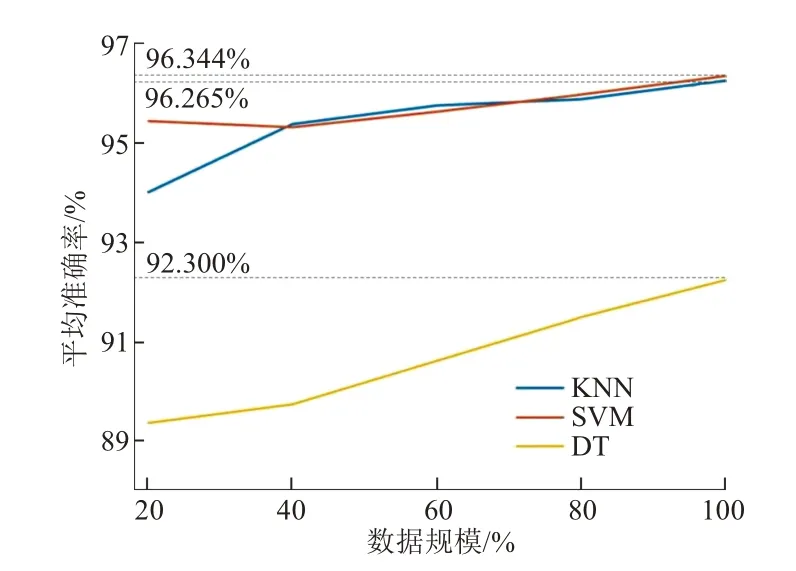
图5 三种分类模型的平均分类准确率随样本数量的变化曲线
4 结论
本文提出一种基于1D⁃DCGAN 的钢轨波磨识别方法。首先使用1D⁃DCGAN 生成的钢轨波磨伪样本进行数据集扩充;然后计算数据的15 种时域统计指标,进行PCA降维,并取前3个主成分分量作为钢轨波磨的特征进行分类模型的训练;最后通过训练好的模型进行钢轨波磨识别。主要结论如下:
1)1D⁃DCGAN 生成的伪样本,在时域、频域和时域统计指标方面都与真实样本基本一致,可以在样本不足时用来扩充数据集。
2)KNN、SVM 和DT 三种分类模型的平均分类准确率都随着训练样本规模增加而增大,其中SVM 的平均分类准确率最高。
