钢筋非均匀锈蚀诱发无砟轨道混凝土轨道板开裂的分析
2022-02-07陈宣东章青顾鑫夏晓舟许骁波邱森烨
陈宣东 章青 顾鑫 夏晓舟 许骁波 邱森烨
河海大学 力学与材料学院,南京 211100
随着我国高速铁路的快速发展,无砟轨道混凝土轨道板得到了广泛应用,覆盖全国大部分地区[1]。轨道板由钢筋、混凝土组成,在沿海地区,氯盐侵蚀诱发的钢筋锈蚀是导致轨道板耐久性失效的主要因素之一[2-3]。因此,研究钢筋锈蚀诱发的轨道板开裂问题对于评估轨道板的服役状态具有重要意义。
在轨道板的浇筑过程中,由于混凝土的水化作用,会在钢筋表面形成一层致密的钝化膜,抑制钢筋的锈蚀[4]。然而,服役环境中的氯盐通过混凝土的孔隙结构逐渐扩散到混凝土内部,并在钢筋表面聚集。当钢筋表面氯离子浓度达到临界值时,钢筋表面钝化膜被破坏,钢筋开始锈蚀[5]。由于钢筋锈蚀产物的体积大于原始体积[6],钢筋与混凝土交界面处产生膨胀应力;当膨胀应力超过混凝土的抗拉强度时,混凝土保护层开始出现裂纹[4];随着侵蚀时间的增加,裂纹不断扩展,进而轨道板的混凝土保护层开裂、剥落,最终导致轨道板结构承载力下降,严重时造成轨道板破坏失效[7]。诸多学者基于数值模拟方法,在钢筋与混凝土交界面施加钢筋锈蚀位移,研究了钢筋锈蚀诱发的轨道板开裂过程[4,8-13]。如,文献[8]基于氯盐侵蚀试验,采用半椭圆函数描述钢筋非均匀锈蚀位移曲线。文献[9-10]采用厚壁圆筒理论,获得均匀锈蚀下保护层锈蚀开裂时钢筋临界锈蚀率。文献[11]基于ABAQUS 软件中的混凝土塑性损伤本构,研究钢筋非均匀锈蚀对轨道板开裂形态的影响。另外,文献[1]建立了轨道板钢筋锈蚀的细观力学模型,研究了温度和列车荷载共同作用下钢筋锈蚀对混凝土保护层开裂的影响。
尽管对钢筋锈蚀诱发混凝土保护层开裂的问题已进行了研究,并建立相关的数值模型,但依然存在诸多问题亟待解决。首先,环境介质侵蚀诱发的轨道板中钢筋锈蚀具有非均匀特性,针对钢筋锈蚀层非均匀分布的表征,国内外学者在试验的基础上建立了高斯分布模型[14]和椭圆模型[10]。这些模型含有较多物理意义不明确的拟合参数,特别是工程上关注的锈蚀率、非均匀度等参数未能直接体现在现有模型中[14]。其次,现有的数值模拟研究多集中在小尺寸上(100~300 mm 混凝土矩形截面)[15],而忽略了结构构造对钢筋锈蚀开裂的影响。再次,钢筋锈蚀诱发保护层开裂的数值模拟研究多基于经典连续介质力学理论[11],但经典连续介质力学理论及数值方法受限于微分方程的连续性要求,并不能很好地描述钢筋锈蚀诱发的轨道板裂纹扩展问题[16]。基于非局部积分思想的近场动力学理论和方法[17-21],避免了传统数值方法采用局部微分方程求解不连续问题时的奇异性等问题。近场动力学具有宏-微观结合与非局部积分特色,与传统方法相比,其具备强大优势,能很好地模拟钢筋锈蚀诱发混凝土保护层裂纹萌生、扩展及剥落[16]。
本文提出以钢筋锈蚀率、最大锈蚀层厚度及最小锈蚀层厚度为自变量的钢筋锈蚀层分布模型;基于近场动力学理论,建立轨道板锈蚀开裂数值模型,研究钢筋锈蚀诱发的轨道板破坏模式,分析钢筋非均匀/均匀锈蚀、保护层厚度对轨道板破坏模式的影响。
1 钢筋非均匀锈蚀诱发保护层开裂的理论模型
1.1 键型近场动力学理论
近场动力学(Peridynamics,PD)是基于非局部作用思想建模并通过求解空间积分方程描述物质力学行为的方法[20-21]。该方法将物体视为大量含有质量和体积的物质点的集合,每个物质点xi与周围有限近场范围内的物质点xj发生相互作用,故近场动力学不采用传统的应力-应变本构,而通过物质点间的键力密度本构建立受力与变形的关系。近场动力学物质点的积分-微分型的运动方程为
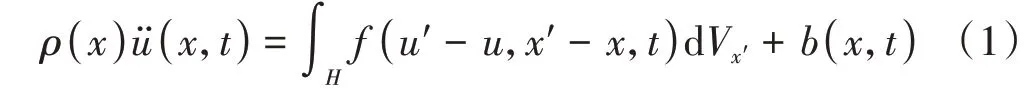
式中:ρ为质量密度为加速度;f为物质点x与x'间的键力密度函数,反映物质点间相互作用的本构信息;u、u'分别为变形前后的位移;近场范围定义为为近场范围半径;Vx'为物质点x'的体积;b为外力密度。
对于均质各向同性材料,键型近场动力学对势键力函数定义为
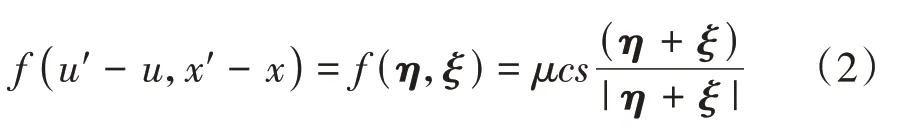
式中:η为相对位移矢量;ξ为相对位置矢量;c为微弹模,不同维度问题的微弹模表达不同;s为键伸长率;μ为表示键损伤的状态变量。
针对钢筋锈蚀诱发轨道板开裂二维分析的平面应变假定,c、s、μ计算式分别为
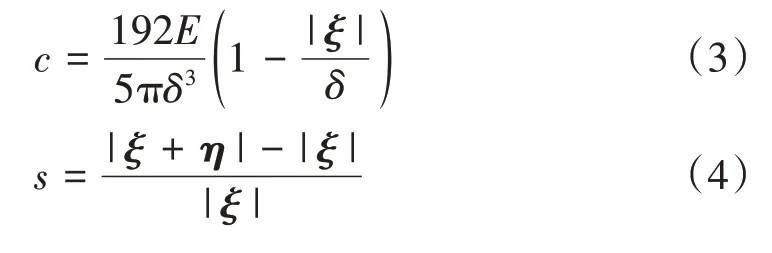
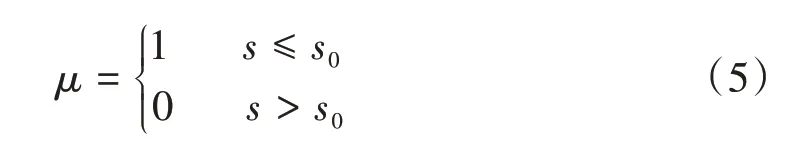
式中:s0为临界伸长率。
s0与材料弹性模量E及断裂能量释放率G0相关[17],计算式为
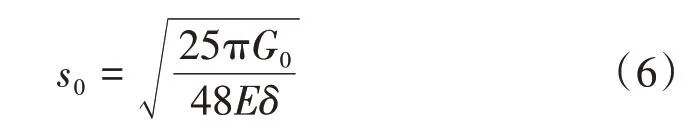
物质点的损伤dc为近场范围内断键数与键总数之比,计算式为
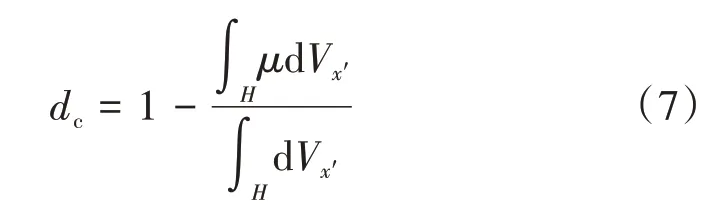
近场动力学运动方程的求解涉及空间离散、时间差分及数值积分方法,缺乏成熟可用软件,需要自主研发。由于钢筋锈蚀过程缓慢,钢筋锈蚀诱发轨道板的破坏过程可近似为准静态,因此采用动态松弛方法(ADR)[16]求解近场动力学控制方程,以高效模拟锈胀力作用下轨道板的准静态开裂破坏。
1.2 钢筋非均匀锈蚀模型
Zhao 等[14]基于钢筋混凝土板的加速腐蚀试验,提出了描述钢筋非均匀锈蚀层分布特征的高斯分布模型,表达式为
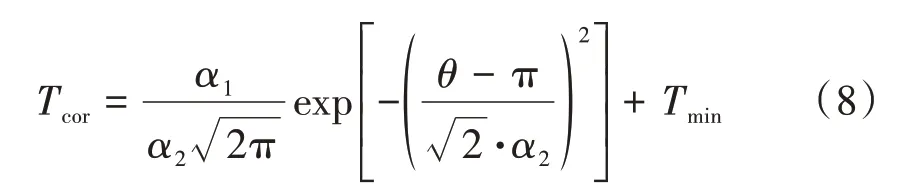
式中:Tcor为钢筋锈蚀层厚度,μm;Tmin为钢筋最小锈蚀层厚度,μm;θ为环绕钢筋的角度;α1、α2为拟合参数。
尽管Zhao 等[14]提出钢筋非均匀锈蚀的高斯分布模型可以很好地反映钢筋锈蚀形态,但模型中的α1和α2物理意义不明确,工程上关注的锈蚀率等参数未能直接反映在现有模型中。在此基础上,本文将建立具有直接物理含义的钢筋非均匀锈蚀高斯分布模型。
钢筋锈蚀率可表示为
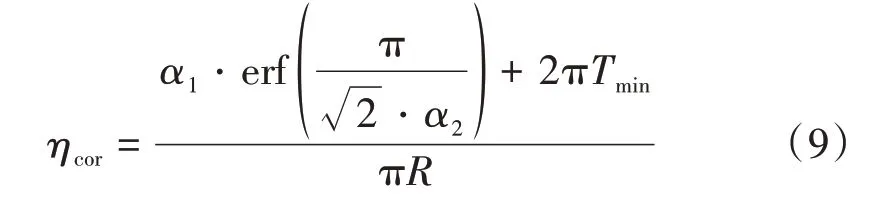
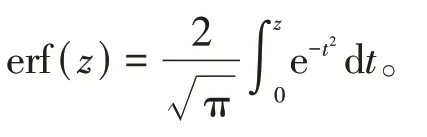
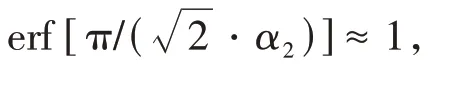
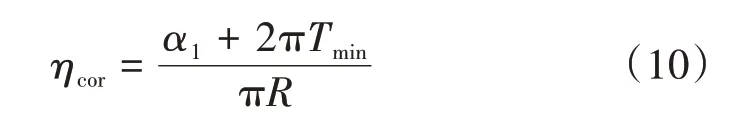
因此,拟合参数α1可以表示为
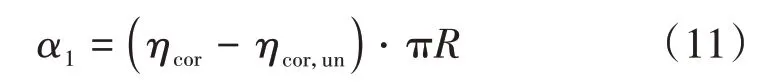
式中:ηcor,un为钢筋均匀锈蚀部分的锈蚀率,ηcor,un=2Tmin/R。
式(8)的钢筋锈蚀层厚度在θ=π 达到最大值Tmax,即

以上,建立了以钢筋最大锈蚀层厚度、最小锈蚀层厚度及锈蚀率为自变量的钢筋非均匀锈蚀的锈蚀层厚度模型。在近场动力学数值计算中,可以通过将锈蚀层分布模型逐级施加在混凝土与钢筋交界面上,实现锈蚀位移边界加载。
2 数值模拟实施
以CRTSⅢ型轨道板为研究对象,轨道板由平面几何尺寸为5 600 mm × 2 500 mm 的重复性单元组成。重复性单元的剖面及配筋信息见图1。考虑轨道板的重复性单元组成特征和对称特性,仅选取重复性单元进行几何建模与数值模拟。由于重复性单元中下部钢筋远离侵蚀面,一般不会发生锈蚀,锈蚀主要发生在上部钢筋[2],故在数值模拟中仅考虑上部钢筋锈蚀。
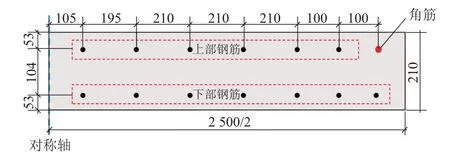
图1 CRTSⅢ型轨道板剖面及配筋信息(单位:mm)
在数值模拟中,混凝土强度等级为C60,弹性模量为36.0 GPa[22],断裂能密度为115 N/m[23]。轨道板计算区域的几何尺寸为1 250 mm × 210 mm,采用1 mm间距的均匀点阵离散结构,共261 068 个方形物质点,见图2。轨道板底侧为固定端约束,左侧为对称边界,其余边界为自由边界。角部钢筋直径为16 mm,其余钢筋直径为12 mm,在钢筋与混凝土交界面处施加位移荷载,每个物质点施加的位移荷载值与钢筋锈蚀深度、锈蚀率及所处位置有关。数值求解流程见图3。图中,i、n为计算步。
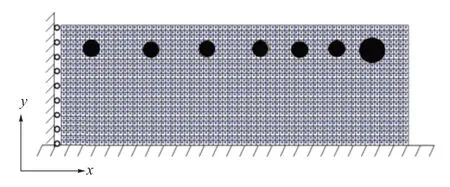
图2 轨道板的近场动力学点阵离散示意
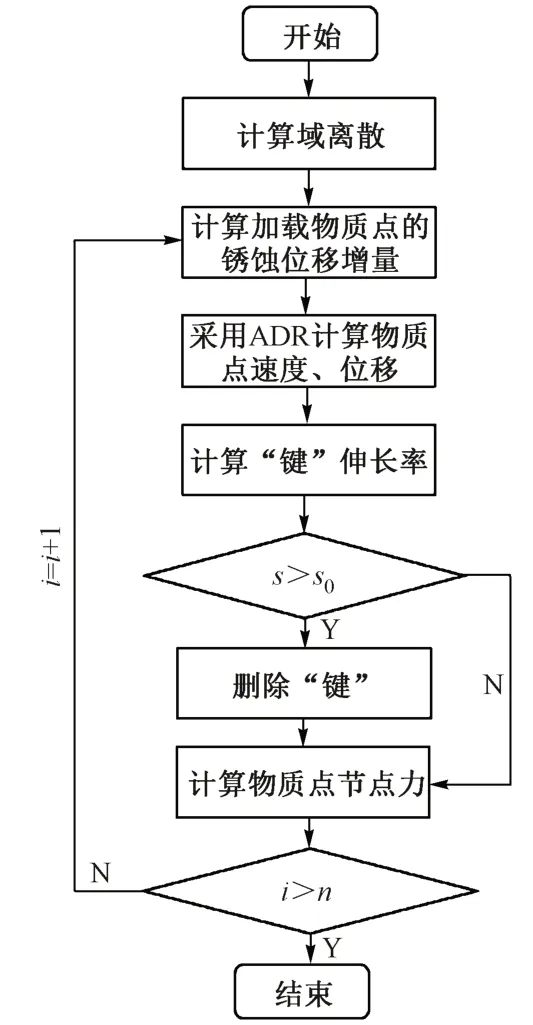
图3 数值模拟流程
3 计算结果分析
3.1 钢筋锈蚀诱发轨道板开裂的破坏模式
钢筋锈蚀率取无砟轨道板的临界锈蚀率0.75%,最大锈蚀层厚度为100 μm,最小锈蚀层厚度为0,保护层厚度为53 mm。共分19 000 个计算步,对应最大加载位移为100 μm,每步均匀加载。钢筋非均匀锈蚀诱发轨道板开裂破坏过程的典型形态见图4。可见,随着计算步增加,轨道板经历了界面处裂纹萌生、裂纹扩展、裂纹贯穿三个阶段。轨道板界面处出现裂纹萌生对应的最大锈蚀位移为26.3 μm,轨道板中形成贯穿性裂纹对应的最大锈蚀位移仅为 89.5 μm。钢筋一旦出现锈蚀迹象,应对轨道板进行修复处理,以免钢筋锈蚀诱发轨道板裂纹贯通,甚至发生局部层裂现象。随着氯盐侵蚀诱发钢筋腐蚀的累积,轨道板最终在混凝土保护层和钢筋间出现贯穿性裂纹,严重影响轨道板的安全服役。
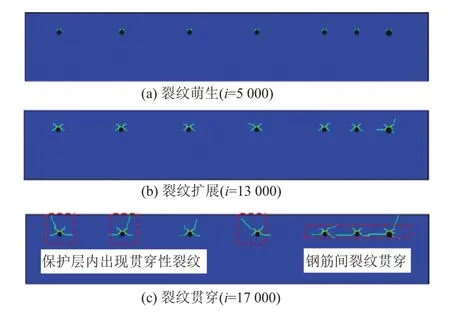
图4 钢筋非均匀锈蚀诱发轨道板开裂破坏过程的典型形态
3.2 钢筋锈蚀非均匀性对轨道板破坏形态的影响
钢筋锈蚀层分布曲线见图5。
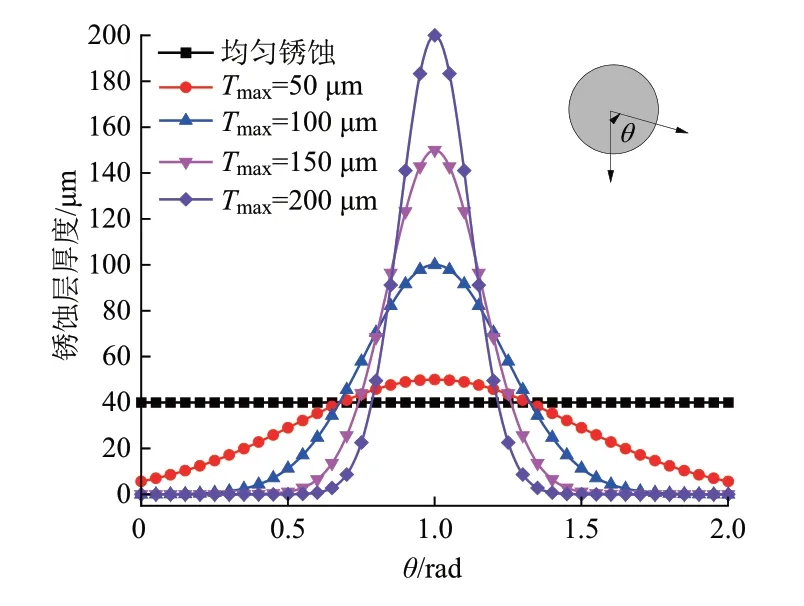
图5 钢筋锈蚀层分布曲线
基于钢筋锈蚀层分布曲线,钢筋均匀锈蚀及非均匀锈蚀诱发的轨道板破坏形态见图6,其中钢筋锈蚀率均为0.75%。可见:对于均匀锈蚀情况,钢筋锈蚀诱发的轨道板的损伤主要集中在钢筋周围,并且有向四周扩展的趋势,但此时轨道板并未出现严重的损伤,如钢筋间裂纹贯通及混凝土保护层出现贯穿性裂纹;对于非均匀锈蚀情况,随着锈蚀的非均匀程度的增加,轨道板出现了钢筋间裂纹贯通及混凝土保护层贯穿性裂纹。模拟结果表明:非均匀锈蚀对轨道板的危害比均匀锈蚀严重,仅采用锈蚀率方式评价钢筋锈蚀对轨道板破坏程度是不合理的,应当考虑钢筋锈蚀非均匀性对轨道板损伤发展的影响。

图6 钢筋均匀锈蚀及非均匀锈蚀诱发的轨道板破坏形态
在相同锈蚀率及锈蚀深度下,贯穿性裂纹首先出现在右侧角部钢筋,表明钢筋直径越大,钢筋锈蚀诱发的轨道板保护层劣化越严重。
试验中均匀锈蚀与非均匀锈蚀下混凝土的典型开裂形态见图7。可见,近场动力学模拟结果与试验结果具有良好的一致性,验证了构建的钢筋非均匀锈蚀诱发轨道板开裂分析的近场动力学方法的可靠性。

图7 均匀锈蚀与非均匀锈蚀下混凝土的典型开裂形态
3.3 保护层厚度对轨道板破坏形态的影响
不同保护层厚度下轨道板的破坏形态见图8,其中,锈蚀率为0.75%,最大锈蚀层厚度为100 μm,最小锈蚀层厚度为0。可知:当保护层厚度为30 mm 时,钢筋锈蚀在保护层内部诱发了贯穿性主裂纹,主裂纹均在保护层内部成一定的角度,主裂纹之间的混凝土出现了剥落现象;随着保护层厚度增加,保护层内部仍有主裂纹扩展演化,但未能贯穿到混凝土表面。同时,由于轨枕下方钢筋间距较小(100 mm),钢筋间形成了连通裂纹,而对于钢筋间距较大的210 mm 区域,钢筋间的裂纹只有相向扩展连通的趋势。因此,保护层厚度和钢筋间距显著影响轨道板的开裂破坏形态。
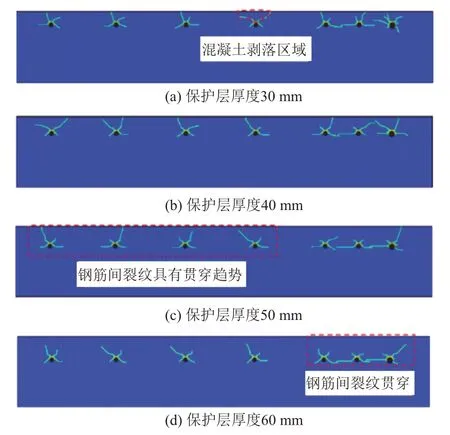
图8 不同保护层厚度下轨道板的破坏形态
4 结论
本文建立了以锈蚀率、最大锈蚀层厚度和最小锈蚀层厚度为自变量的锈蚀层厚度分布模型,基于键型近场动力学理论,通过在钢筋与混凝土交界面施加锈蚀位移荷载,数值模拟了钢筋锈蚀诱发轨道板开裂破坏过程。得到以下结论:
1)随着钢筋锈蚀程度的加深,钢筋锈蚀诱发了轨道板混凝土保护层内出现两种裂纹形态:保护层内的贯穿性裂纹及局部钢筋间裂纹连通;实际工程中应采用无损检测手段,探明轨道板内是否发生钢筋间裂纹连通。
2)钢筋锈蚀非均匀性对轨道板的破坏形态具有显著影响。与均匀锈蚀相比,非均匀锈蚀对轨道板的损伤更加严重。实际工程中在评估钢筋锈蚀对轨道板破坏产生的影响时,应考虑锈蚀的非均匀性。
3)随着保护层厚度的增加,钢筋锈蚀诱发的保护层裂纹有可能还未扩展到保护层表面,而保护层内部及钢筋间已经形成宏观性裂纹。同时,钢筋间距较小时,钢筋间的裂纹容易连通,进而增加保护层剥落的风险。
