基于组合赋权—SPA 的采空区围岩稳定性研究

祁 云 汪 伟 刘 娇 葛佳琪 周倍淇 张孟浩 齐庆杰

(1.山西大同大学煤炭工程学院,山西 大同 037000;2.辽宁工程技术大学安全科学与工程学院,辽宁 阜新 123000;3.中国安全科学学报编辑部,北京 100011;4.中国矿业大学(北京)应急管理与安全工程学院,北京 100083;5.晋能控股集团塔山煤矿,山西 大同 037000;6.中国煤炭科工集团应急科学研究院,北京 100013;)

采空区围岩失稳是矿山开采最常见的事故之一, 采空区围岩失稳不仅直接威胁工作人员和设备的安全,而且也增加了矿山开采活动的难度与阻力[1]。随着全国浅部矿产资源的枯竭,矿山开采逐步向深部高应力集中区转移,围岩内积聚的大量势能受采动影响急剧释放,围岩失稳事故愈发严重[2]。科学准确地评价采空区围岩稳定性是控制和规避采空区失稳灾害的重要措施,但是由于影响采空区稳定性的因素存在随机性、突发性和不确定性等特点,采空区围岩稳定性的准确评判与预测存在较大难度[3]。因此,研究如何提高采空区围岩稳定性评价结果具有重要意义。

目前,采空区围岩稳定性评价主要有数值模拟分析法和以模糊数学理论为基础的建模分析法。其中数值模拟分析法能够从时空关系上直观地揭示采空区失稳变形的过程,但需要提前对各控制条件进行理想化假设,使得分析结果与实际情况具有较大差异,难以在现场实践中得到应用[4-6]。建模分析法虽不能直观反映采空区失稳变形的过程,但该方法能够模拟人的思维过程、逻辑性较强且计算结果准确可靠。近年来,众多学者广泛采用多种建模理论和方法研究采空区围岩的稳定性,汪伟等[7]建立遗传BP 神经网络辨识模型,得出了训练样本与检验样本平均误差仅差0.4%,有效辨识了采空区危险等级。赵国彦等[8]基于模糊熵原理改进云模型,建立采空区稳定性二维评判模型,并引入模糊熵表征采空区稳定性的复杂程度。王海峰等[9]通过引入支持向量机理论,利用有向无环图构建了采空区稳定性分级模型,计算结果真实地反映了采空区稳定性的实际情况。王正帅等[10]针对采空区不稳定性因素特点建立模糊可拓评价模型,通过分析综合关联度确定采空区稳定性等级。胡建华等[11]基于粗糙集理论建立采空区危险性判别模型,对比分析采空区三维数值模拟结果验证了判别模型的正确性。黄亮等[12]基于偏序集理论构建采空区危险性评价模型,通过Hasse 图展现的采空区危险性层集信息判断其危险程度。上述采空区稳定性评价方法对采空区围岩失稳问题的防治起到了一定的推动作用,但是由于影响采空区稳定性的因素较为复杂且具有模糊性、不确定性,指标的定性分析向定量分析转化过程中误差较大。

鉴于此,本研究拟将改进的AHP 法、EWM 法和SPA 理论引入采空区围岩稳定性评价中,旨在消除主、客观因素对指标权重的影响以及边界模糊性对SPA 法的影响,建立改进组合权—SPA 的采空区围岩稳定性评价模型,以期为采空区围岩稳定性准确预测提供新方法。

1 组合权的确定

1.1 改进AHP 指标权重确定

为了避免AHP 法判断矩阵一致性检验的盲目性与主观性问题,采用3 标度法构建各指标重要度判断矩阵[13-14],并基于最优传递矩阵的性质,设置AHP 法自动调整器,通过构造反对称矩阵和最优传递矩阵将判断矩阵转换成拟优化一致矩阵,然后利用方根法计算层次单排序获取主观权重,具体步骤如下:

(1)建立采空区稳定性评价系统递阶层次结构模型。分析采空区围岩稳定性评价各指标的联系与影响,结合专家意见,将各指标进行层次化分解,确定上下层指标间的隶属支配关系。

(2)构造判断矩阵。为了反映隶属于同一约束的不同指标两两比较的重要关系,采用3 标度法对各约束条件下的指标进行重要性比较,构造比较矩阵:

式中,aij为比较矩阵中因素i相对于因素j的重要性且满足aii=0,aij+aji=0。aij=1,指标i比j重要;aij=0,指标i与j同等重要;aij=-1,指标i不如j重要。

(3)自动调整器的设置。

① 反对称矩阵的构建。引入对数函数对比较矩阵An×n中各元素aij进行变换,构建反对称矩阵Bn×n=(bij)n×n。

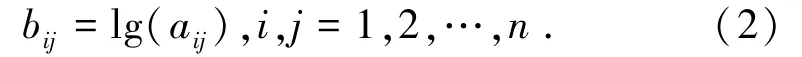
② 最优传递矩阵的确立。为了尽可能地减少人为误差,降低劣质反对称矩阵中劣质元素对评判结果的影响,采用线性加权法把Bn×n种各元素进行下式变换,得到最优传递矩阵Cn×n=(cij)n×n。

③ 拟优化一致矩阵。引入指数函数优化Cn×n中各元素,进而得到拟优化一致矩阵Vij=(vij)n×n。

(4)各指标层次单排序。为了简化权值的计算过程,各指标权值采用实际应用较广泛且能够保证权值可靠性的乘积方根法进行计算。其计算式为

1.2 EWM 法主观权重确定

熵权法(EWM)是一种根据各指标的有效信息变异程度大小确定客观权重的方法[15]。若指标的有效信息变异程度越大,则其提供的信息量就越大,所占权重就越高。EWM 法计算权重步骤如下:

(1)构造决策矩阵X。按照定性与定量结合的原则对围岩稳定性评价的m个样本,n个围岩稳定性评价指标的原始数据矩阵D=(dij)m×n进行无量纲、标准化处理构造决策矩阵X=(xij)。

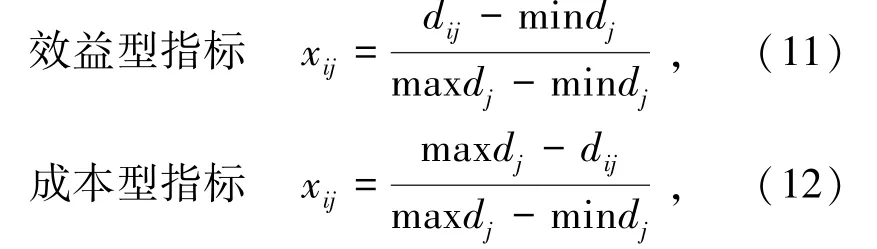
式中,mindj、maxdj分别为针对某一指标不同评价因素相对效益型指标和成本型指标的贴近值。

(2)确定评价指标熵值。为了避免指标特征比重值为零,确保评价指标熵具有数学意义,并将xij·lnxij对指标熵的影响控制在合理范围内,需要对决策矩阵中部分元素进行修正,进而确定评价指标熵值。

式中,yij为评级指标特征比重;ψ为修正系数;ej为第j项指标熵权值。

(3)计算第j项指标的信息权重:

1.3 改进组合权的确定

为了确保决策者对采空区围岩稳定性指标的主观认识和客观调查数据能够真实地反映围岩稳定性变化特征,引入折衷系数耦合各指标因素的主观、客观权重,建立改进的决策模型;通过引入n维空间的欧几里得度量,保证主、客观权重与折衷系数间的差异度保持一致,最终得出组合权的理想值:

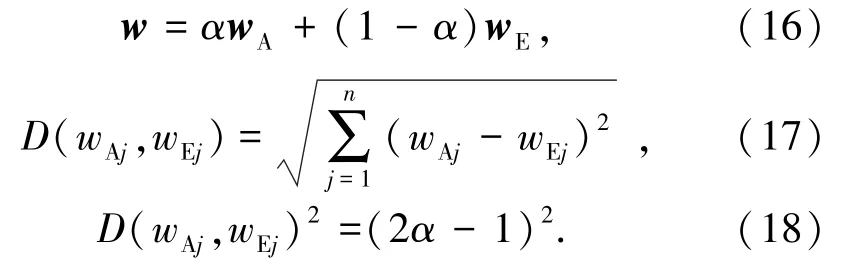
式中,α为权重折衷系数;D(wAj,wEj)为欧几里得度量;D(wAj,wEj)2为主、客观权重与折衷系数的差异度。

2 改进组合权耦合SPA 评判模型

2.1 构建集对分析(SPA)模型

基于工程实际中对评价精度的要求,传统的集对分析(SPA)理论中同异反联系度模型显得过于粗糙、简单,且只能处理确定的分级标准,无法区分评判指标处于相邻或间隔时的等级差异[16-17]。为此,需要对传统的联系度可展性进行优化。

(1)假设多因素评判集U={u1,u2,…,un},所邀m位参评专家对评判因素us(1≤s≤n)的评判指标等级P={p1,p2,...,pm},则评判目标关于评判因素us的同异反评价为rs1+rs2i+…+rsm-1i+rsmj,i为差异度系数,i∈[-1,1];j为对立度系数,j=-1;其中rs1+rs2+…+rsm-1+rsm=1,进而得到初始同异反评价矩阵:

(2)评判集合或集对在某种背景条件下的同一度、差异度和对立度系数构成同异反多元系数矩阵E=(1,i1,i2,…,im-2,j)T,与评判集U中各指标因素的权重向量W=(w1,w2,…,wn)构造出赋予评判指标权重集对分析的同异反评价模型:

即:

2.2 构建改进组合权耦合SPA 综合评判模型

设第s个评价对象的联系度us,对评判指标中第k项指标进行集对分析得到其联系度usk,结合上述改进组合权的计算构造赋予各指标组合权重集对分析模型:

结合式(16)、式(20)、式(21)可以得出:

改进组合权耦合SPA 综合评判模型充分利用集对分析理论兼顾评价指标的不确定性特点,同时引入组合权重对评判指标进行定量化,优化采空区围岩稳定性评判模型,以提高评价结果的准确度。为了更直观展示评价过程,绘制采空区围岩稳定性评价流程,见图1所示。

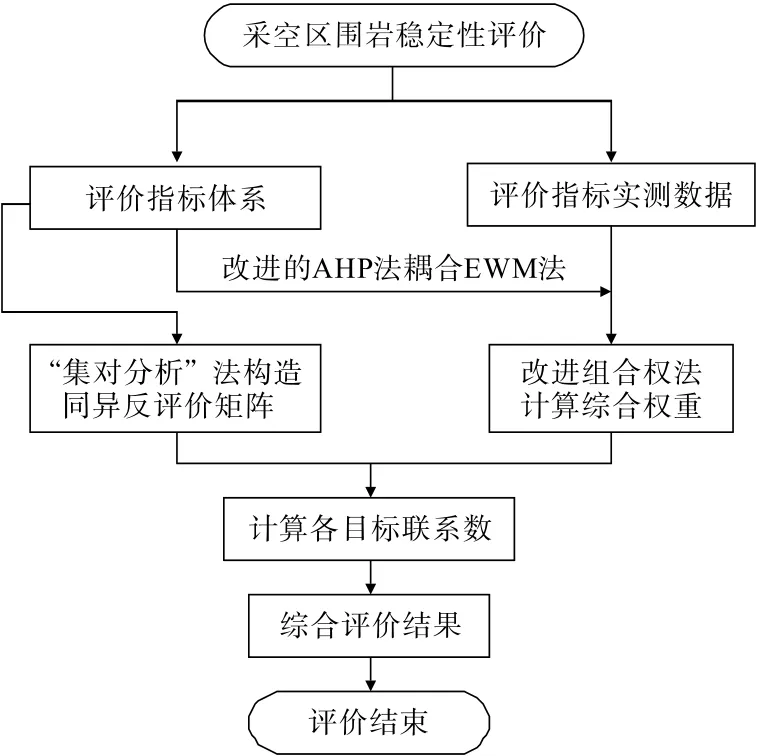
图1 综合评价流程Fig.1 Comprehensive evaluation process

3 采空区围岩稳定性评价实例

3.1 采空区围岩稳定性评判指标

采空区围岩稳定性是多因素共同作用的结果,一般认为具有失稳破坏倾向性的采空区围岩在持续的采动扰动影响下应力逐渐积聚至大于岩石的抗压强度后才会引起其变形破坏,由于采动扰动、岩石抵抗强度随工作面推进距离的变化呈现动态变化,综合考虑影响采矿区围岩稳定性的因素,根据山西某矿己组煤层实际情况和参考文献[13]的基础上,建立以岩体结构、地质构造、采动扰动和岩石抗压强度为主要因素的具有11个单项指标的采空区围岩稳定性评价指标体系,见表1。参考文献[14]将采空区稳定性划分为Ⅰ、Ⅱ、Ⅲ和Ⅳ级,分别表示稳定、较稳定、基本稳定和不稳定4种状态,见表2。则评价对象相对于评价因素us的同异反评价为rs1+rs2i+rs3i+rs4i+rs5j,其中,rs1+rs2+rs3+rs4+rs5=1。基于“均分原理”取i1=0.5、i2=0、i3=-0.5、j=-1,将其代入联系度表达式中计算联系度值即可求得其对应的稳定性等级。

表1 采空区围岩稳定性评价体系Table 1 Evaluation system of goaf stability

表2 等级划分及判断区间Table 2 Grade division and judgment interval

3.2 “AHP+EWM”综合权重的确定

通过比较法分析山西某矿己组采空区围岩稳定性评判指标间的重要程度,采用3标度法对其量化构造判断矩阵,并根据式(1)～式(7)求出其最大特征值所对应的特征向量:w=(0.333 3,0.333 3,0.333 3) ,w1=(0.387 3,0.169 8,0.442 9),w2=(0.490 5, 0.311 9,0.197 6) ,w3=(0.336 2,0.265 6,0.221 2,0.088 5,0.088 5) ,然后利用式(8)～式(10)对特征值进行一致性检验,所求各判断矩阵的CR值均小于0.1,故判断矩阵和特征向量符合要求,则采空区围岩稳定性评判因素AHP权重向量为:wA1=(0.387 3,0.169 8,0.442 9) ,wA2=(0.490 5,0.311 9,0.197 6) ,wA3=(0.336 2,0.265 6,0.221 2,0.088 5,0.088 5)。然后根据表1中数据,分别对评判对象的原始数据进行无量纲规范化处理,通过式(11)～式(15)得出采空区围岩稳定性因素EWM法的权重量:wE1=(0.302 1,0.341 3,0.356 6),wE2=(0.296 8,0.329 4,0.373 8) ,wE3=(0.179 6,0.166 6,0.200 8,0.230 3,0.222 7)。

引入欧式距离函数将AHP 法主观权重与EWM法客观权重进行结合,并根据式(16)～式(18)得折衷系数α为0.73,最终求出各评判指标的理想综合权重为w1=(0.364 3,0.216 1,0.419 6),w2=(0.438 2,0.316 6,0.245 2),w3=(0.293 9,0.238 9,0.215 7,0.126 8,0.124 7)。各指标综合权重雷达图如图2所示,由图2 可知,不同评判指标对采空区围岩稳定性的影响具有一定差异,影响采空区围岩稳定性的主要因素呈U21＞U13＞U11＞U22＞U31的关系,可将其作为采空区稳定性防治的主要判据。

图2 各指标综合权重Fig.2 Comprehensive weight of each index

3.3 采空区围岩稳定性等级的确定

依据评判指标体系,利用文献[14]中收集的山西某矿采空区数据,针对3 个待预测的采空区评判指标因素邀请理论知识扎实、实践经验丰富的专家进行打分评判,对评判结果归一化处理,见表3。

表3 待评采空区及单指标评价结果Table 3 Goaf to be evaluated and single index evaluation results

根据式(20)计算得出1 号采空区评判结果联系度表达式为

同理

同理2 号采空区评判结果联系度表达式为

3 号采空区评判结果联系度表达式为

经计算各采空区评价结果可得1 号和3 号采空区的平均联系度值分别为0.213 8和0.371 2,其评判等级均为II 级(较安全);2 号采空区的平均联系度值为0.170 8,其评判等级为Ⅲ级(一般安全),见表4。由表4 分析可得评判结果与采空区围岩稳定性实际情况相吻合,说明评判模型对采空区围岩稳定性预测结果准确,具有一定的普适性,具有指导意义。

表4 采空区稳定性评判结果Table 4 Evaluation of rock burst tendency

4 结 论

(1) 针对采空区围岩稳定性评价中各指标因素的确定性与不确定性间的相互影响问题,提出了改进组合权—SPA 的采空区围岩稳定性评判模型,引入折衷系数、欧氏距离函数优化决策模型,减少AHP 法的主观性、经验性与EWM 法的客观性对评判结果的影响,使得综合权重更加符合实际,进而获得较准确的SPA综合联系度参数,为采空区稳定性评价提供新思路。

(2)通过改进组合权法确保了采空区围岩稳定性预测各指标因素的权重分配合理,但分析各指标的权重值表明,采空区围岩稳定性影响因素对稳定性影响的程度具有差异性,影响山西某矿采空区稳定性的主要因素呈U21＞U13＞U11＞U22＞U31的关系。

(3)改进集对分析法对1 号、2 号和3 号采空区围岩稳定性预测结果与实测结果基本保持一致,仅1 号采空区评判结果相对保守,但从危险性角度看评判结果可信度更高,这可能与该矿岩石抗压强度实测结果偏高现象相符合。

(4)基于改进组合权耦合SPA 的采空区围岩稳定性评价模型对山西某矿进行预测时,计算结果不但能够清楚有效地反映各评判指标的级别,还能根据各指标的联系度参数对其危险等级进行排序,使得评判结果具有较高的准确度,为采空区围岩失稳事故的合理管控提供依据。