风电机组虚拟惯量控制的应用方法研究
2022-02-06柴斌侍乔明摆世彬王永平刘若鹏
柴斌,侍乔明,摆世彬,王永平,刘若鹏
(1.国网宁夏电力有限公司超高压公司,宁夏 银川 750011;2.南京南瑞继保工程技术有限公司,江苏 南京 211102;3.国网宁夏电力有限公司,宁夏 银川 750001)
0 引 言
随着我国风电装机容量的不断增加,风电在电网中渗透率不断提升。由于传统的风电机组并网存在的解耦特性,使得风电机组在最大功率跟踪控制方式下不会响应系统频率的变化,无法为电网提供惯量和一次调频支持,这给电力系统的频率稳定带来了巨大挑战[1-3]。
风电虚拟惯量控制能够使得风电机组响应系统频率的变化,为电网提供惯量和暂态调频支持[4]。相比传统的同步发电机组,风电机组通过虚拟惯量控制参与电网调频存在自身的特点和限制[5]。目前,风电参与电网调频的研究主要从风电场协调控制角度开展[6-7],实际风机参与调频时,为了保证风电机组参与调频的快速性,风电机组需自身能够自动检测系统频率,调整风机出力,然后自动恢复正常运行状态,因此,要实现虚拟惯量控制在风电机组中的实际应用,还需要考虑风电机组的频率响应特点,进一步研究虚拟惯量控制在风机实际执行的时序。
针对风电机组参与电网调频存在的特点和限制,以直驱永磁风力发电机组(directly-driven wind turbine with permanent-magnet synchronous generator,D-PMSG)为研究对象,基于已有的比例微分(proportion differential,PD)虚拟惯量控制方法,提出了一种实用的风电虚拟惯量控制方法,给出了该方法在实际风电机组中应用的具体步骤,并通过仿真分析和实验测试,验证了所提方法在实际风机中应用的可行性。
1 风电虚拟惯量控制的原理及特点
1.1 风电PD虚拟惯量控制的基本原理
D-PMSG主要由风力机、传动轴、永磁发电机(permanent-magnet synchronous generator,PMSG)、全功率变流器(full-power converter,FPC)及其控制系统组成,其中,风力机直接驱动PMSG 旋转发电,全功率变流器实现对PMSG 输出功率的变换与控制。D-PMSG机组并入电网后系统结构如图1所示。
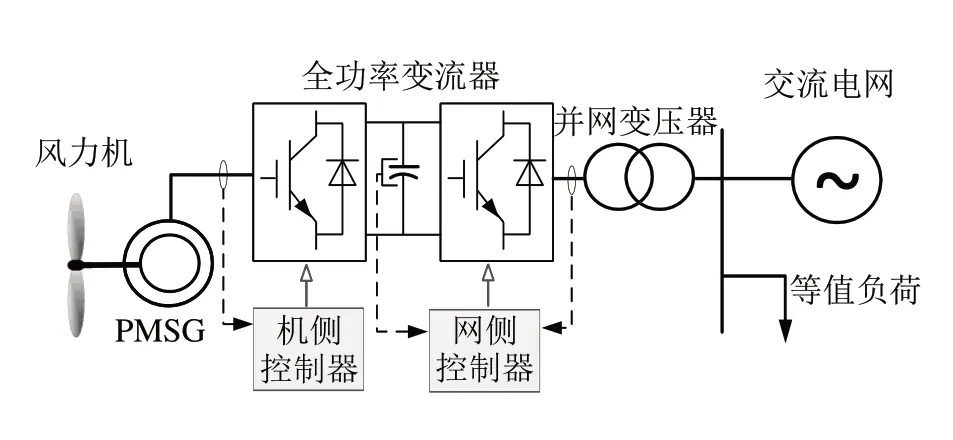
图1 D-PMSG 并网系统结构
图1中,风力机捕获的风电功率Pwind的表达式[8]为

式中:ρ为空气密度;r为风轮的半径;v为风速;Cp为风力机的功率系数;θ为桨距角;λ为叶尖速比;λ=ωwr/v;ωw为风力机风轮的转速。
D-PMSG 机组PD 虚拟惯量控制是在风电机组最大功率跟踪控制(maximum power point tracking,MPPT)的基础上,引入与系统频率偏差比例、微分量相关的辅助功率PVIC,使风电机组在系统频率波动时改变其出力,实现对传统同步发电机组一次调频特性和惯性响应特性的模拟,其原理如图2所示,图中,PVIC表达式[3]为
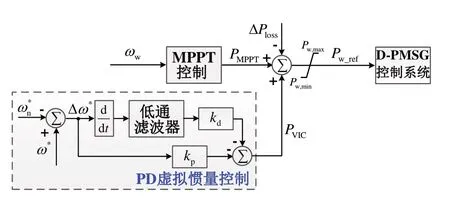
图2 风电PD虚拟惯量控制的原理
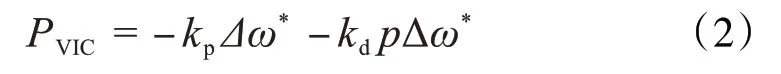
式中:p为微分算子;kp、kd分别为比例、微分控制系数;Δω*为系统频率偏差量的标幺值,Δω*=ω*-1,ω*=ω/ωn;ω为系统角频率;ωn为系统的额定角频率。
风电机组的参考功率Pw_ref由MPPT控制输出功率PMPPT和虚拟惯量控制辅助功率PVIC组成,即

PMPPT表达式[9]为

式中:kmax为使风力机捕获风能达到最大值的控制系数,其数值为0.5ρπr5Cpmax/λopt3;Cpmax、λopt分别为最优功率对应的功率系数和叶尖速比。
1.2 风电机组通过虚拟惯量参与电网调频的特点
风电机组虚拟惯量控制引入前后的系统频率响应特性对比结果如图3所示。图中,未引入虚拟惯量控制时,风电机组工作在MPPT 控制状态,风电机组不响应系统频率变化;虚拟惯量控制引入后,系统频率波动时,D-PMSG通过改变机组的出力参与电网调频,有效降低了系统频率的下降速率,减小了系统频率波动的最大偏差值。
从图3特性可见,相比传统同步发电机组,D-PMSG通过虚拟惯量控制参与电网调频具有如下特点:
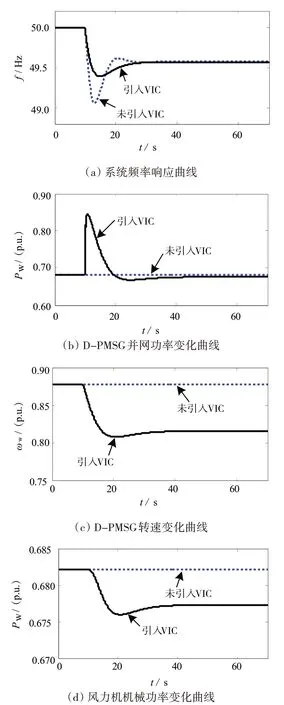
图3 风电机组引入虚拟惯量控制前后系统的频率响应特性对比
1)快速性和可控性。全功率变流器具有快速、灵活的响应特点,D-PMSG 的出力能够根据需求进行快速调节,从而为系统提供快速的有功支撑。
2)暂时性。D-PMSG 主要通过调节机组出力、改变机组的转子动能来为系统提供调频支持,在这个过程中,由于风机转子动能的有限性,一方面,需要考虑风机转速的限制,保证风机转速在一定范围(如0.6~1.0 p.u.)内变化,防止风机因转速过低而引起风机停机;另一方面,风机参与电网调频过程后,由于其转子转速偏离了最优转速,因此需要考虑通过转速恢复控制使机组转速回到最优转速,从而保证机组的发电效率。
2 风电机组虚拟惯量控制方法的应用
2.1 实用的风电机组虚拟惯量控制策略
一种实用的PD 虚拟惯量控制方法的原理如图4所示。
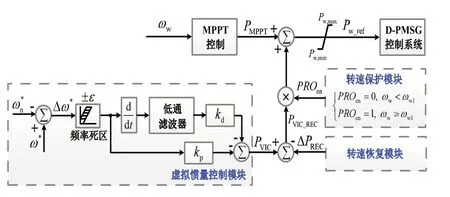
图4 实用的PD虚拟惯量控制策略
该方法主要从以下三个方面进行了改进:
1)频率事件的检测。风电机组通过虚拟惯量控制参与系统调频,主要目的是应对系统中的较大或异常负荷波动,对于系统中幅值较小的负荷波动则可以不用响应。为了保证机组的发电效率,有必要设置系统响应的死区,使得虚拟惯量控制只有在系统频率超过死区时才动作。另外,虚拟惯量控制主要改善的是系统频率的暂态特性,而对于系统频率的静态偏差,风电机组则无法也不需要响应。因此,风电机组虚拟惯量控制启动条件为系统频率超过频率区间[fL,fH]且系统频率变化率|df/dt|大于阈值δf。
2)转速保护模块。风机转速较低时,由于机组的转子动能较小,风机虚拟惯量控制容易导致机组转速的快速下降,严重时容易引起机组停机。因此,引入转速保护模块,当风机转速低于安全值ωw1时,通过将转速模块使能置零,从而使风机直接退出系统调频。
3)转速延时恢复模块。风电机组通过虚拟惯量控制参与系统暂态调频后,由于调频过程中转子动能的改变使得转速偏离最优值,同时由于下垂控制环节的存在,虚拟惯量控制所得的辅助功率PVIC=-kpΔω*≠0,这使得机组在偏离MPPT 点处再次达到稳定。因此,只要系统频率存在偏差(范围超过死区),风电机组转速就不会自动恢复到最优值。风电机组转速偏离最优值,不仅影响风电机组的发电效率,同时还会影响机组再次参与系统调频的能力。考虑到系统二次调频的时间较长,异常负荷扰动后,系统频率偏差将会较长时间存在。因此,主动参与系统暂态调频后,风电机组有必要采用适当的控制方法,使风机转速及时恢复到最优值。
2.2 风机转速恢复控制方法
风电机组转速恢复控制的本质是逐渐减小PVIC直至其等于零,从而为风机提供一个趋向最优转速的加速转矩。转速恢复控制的常用方法是在PVIC的基础上叠加一个与之相反的补偿功率ΔPREC,从而抵消PVIC的作用。图4中,经转速恢复控制补偿后,风机实际添加的调频辅助功率为PVIC_REC,PVIC_REC=PVIC-ΔPREC。
目前常用的转速恢复控制方法是采用(proportional integral,PI)控制器来得到补偿功率,其原理如图5所示。图中,ωw0为风机转速参考值(MPPT 控制所对应的转速),ΔPREC为进行转速恢复而产生的补偿功率,触发信号控制转速恢复过程的起停。
采用图5所示的PI 转速恢复方法存在PI 参数难以选择的问题:若PI 参数取值过小,则风机转速恢复速度会较慢;若PI 参数取值过大,则容易导致风机有功出力变化幅度过大,从而给系统频率带来二次影响。同时,PI 转速恢复方法中,补偿功率ΔPREC的大小完全由风机转速偏差的大小来决定,因此无法很好地预估和控制转速恢复对系统频率二次影响的大小。
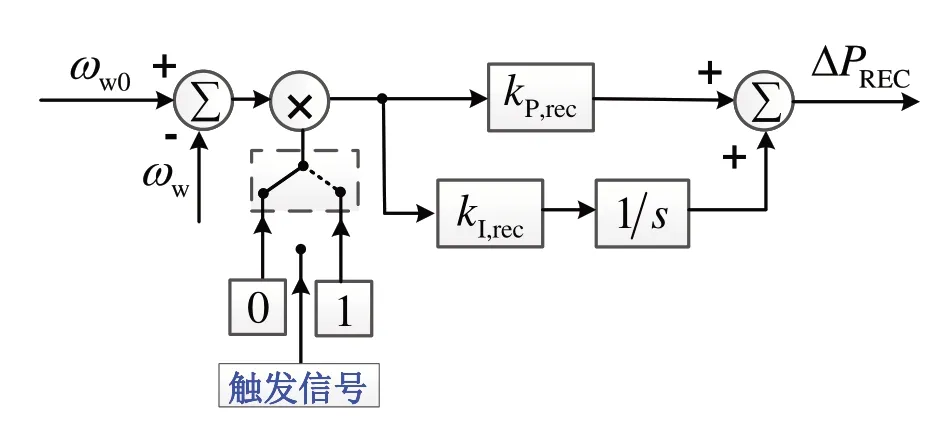
图5 比例积分转速恢复控制原理
考虑到转速恢复控制的本质是逐渐减小PVIC_REC直至其等于零,从而使风机主动退出虚拟惯量控制。因此,通过直接对虚拟惯量控制模块输出的调频辅助功率PVIC进行补偿来实现风电机组转速的恢复控制,其原理如图6所示。

图6 风机转速恢复控制方法
补偿功率的表达式如式(5)所示:
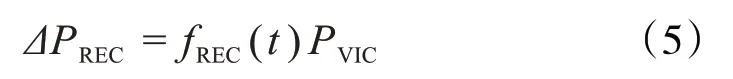
式中:fREC(t)为补偿函数,风电机组的转速恢复过程由该函数决定。
当机组转速低于最优转速时,风电机组需要通过减小机组出力来增加转子动能,从而实现转速的恢复。这个过程中,风机出力的减小必然会对系统频率产生二次影响,这是无法避免的。然而,合理的转速恢复过程可以尽量减小这种影响,采用如下函数实现平滑过渡:
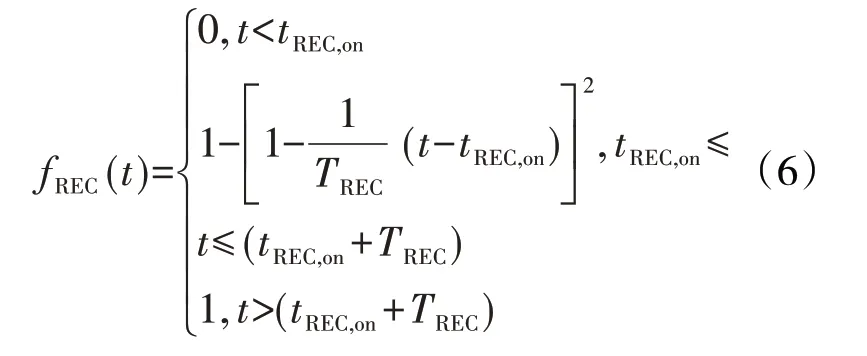
式中:tREC,on为转速恢复控制的启动时刻;TREC为转速恢复过程持续的时间。补偿函数的变化曲线如图7所示。

图7 转速恢复控制函数值的变化曲线
转速恢复过程中,转速恢复启动时刻和持续时间的不同均会对系统频率产生影响。由于系统惯性响应的过程通常为5~10 s,因此,转速恢复通常在虚拟惯量控制启动后的5~10 s内启动。对于风机转速恢复的持续时间,考虑到电网频率的一次调节时间通常为10~30 s,因此可选择的30 s。
图8为D-PMSG 在未引入转速恢复控制和采用式(5)和式(6)所示的转速恢复控制条件下所对应的响应过程。
图8中,tVIC,on为虚拟惯量控制启动的时刻,tREC,on和tREC,off分别为转速恢复启动和完成的时刻,tREC,on-tVIC,on=10 s,转速恢复过程持续的时间TREC=25 s,tREC,off=tREC,on+TREC。从图8(b)中可见,D-PMSG通过减小机组输出的电磁功率,使其小于风力机的机械出力,从而实现了转速的恢复。

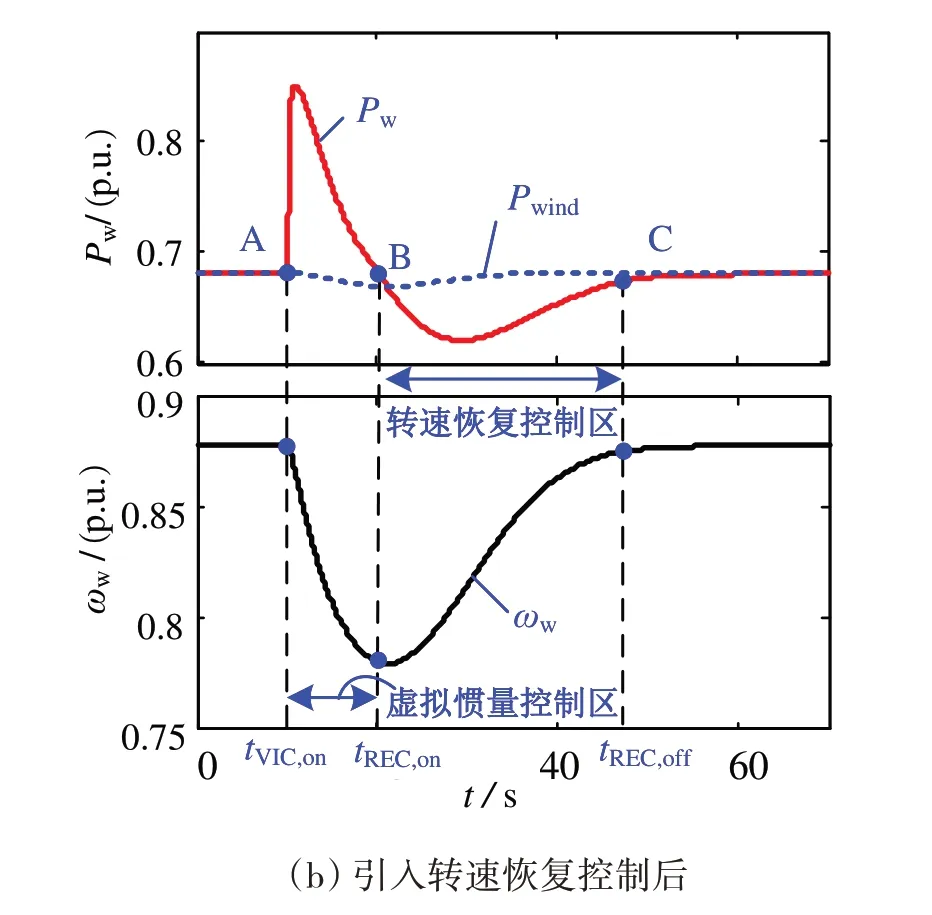
图8 转速恢复控制引入前后D-PMSG的响应特性对比
图9为不同转速恢复控制参数条件下的系统频率响应曲线对比,其中,转速恢复case1 代表tREC,on-tVIC,on=10 s,TREC=25 s 时的响应曲线,转速恢复case2 代表tREC,on-tVIC,on=5 s,TREC=35 s 时的响应曲线。从图9中可见,通过调整转速恢复控制启动的时刻和持续时间,不仅能够实现风机转速的恢复控制,同时可以有效控制风机转速恢复过程对系统频率产生的二次影响。
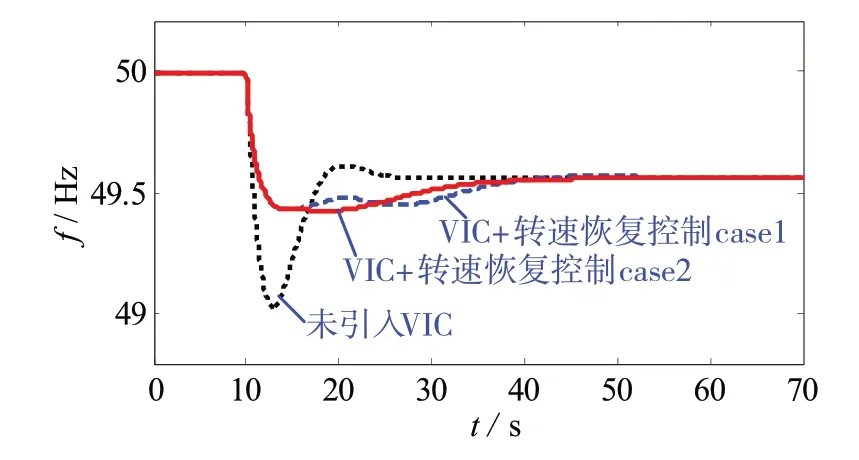
图9 不同转速恢复控制参数下的电网频率特性对比
2.3 风电机组虚拟惯量控制应用的实施步骤
1)频率事件检测。当系统频率超过频率区间[fL,fH]且系统频率变化率|df/dt|大于阈值δf时,虚拟惯量控制模块使能位VICen置1,即VICen=1,此时,虚拟惯量控制模块启动,此时刻记为tVIC,on。
2)虚拟惯量控制过程。当VICen=1 时,风电机组参与系统频率的暂态响应控制。由于虚拟惯量控制仅提供暂态调频支持,因此虚拟惯量控制有效作用的时间TVIC通常为5~10 s。虚拟惯量控制过程中,ΔPREC=0,PVIC_REC=PVIC。
3)转速恢复过程。当t>(tVIC,on+TVIC)且VICen=1时,转速恢复使能位RECen置1,转速恢复控制过程启动。转速恢复启动的时刻记为tREC,on,tREC,on=tVIC,on+TVIC。经转速恢复控制补偿后,风机实际添加的虚拟惯量调频辅助功率PVIC_REC=PVIC[1-fREC(t)]。
4)MPPT运行。当t>(TREC+tREC,on)时,PVIC_REC=0,转速恢复过程完毕,将VICen和RECen置为零,此时机组退出此次调频过程,恢复到MPPT 运行状态,等待参与下一次系统频率控制。转速恢复控制结束的时刻记为tREC,off,tREC,off=tREC,on+TREC。
上述过程完成后,虽然系统频率可能仍存在一定的静态偏差,但由于不满足虚拟惯量控制模块启动的条件,因此风电机组虚拟惯量控制不会启动。
3 实验验证
3.1 实验系统
为了进一步验证本文所提的虚拟惯量控制应用方法在实际风机电机组中应用的可能性,搭建了一套系统容量为35 kVA 的模拟风电并网实验系统[10],系统的结构如图10所示。实验系统主要包含两套7.5 kW 的模拟D-PMSG 机组及一套20 kVA 的模拟同步发电机组,每套模拟D-PMSG包含模拟风力机、PMSG、全功率变流器、并网变压、模拟同步发电机,用换流器基于虚拟同步发电机算法进行模拟。实验过程中,风电虚拟惯量控制算法基于实际的风电变流器控制器来实现。
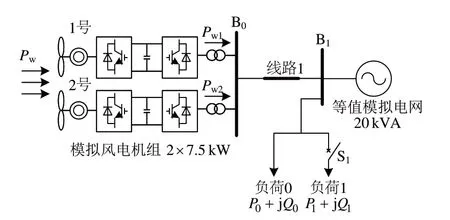
图10 直驱永磁模拟风电并网实验测试系统
图10中,1 号和2 号模拟D-PMSG 的风机风速分别设置为9.5 m/s 和7.0 m/s,系统初始负荷P0为20 kW,突加4.3 kW(21.5%)的负荷扰动,分别在无虚拟惯量控制和所提的实用虚拟惯量控制方式下进行实验对比。所提实用虚拟惯量控制方法中,kp=2.14×105,kd=3.42×105,ωw1=0.6ωwn,系统负荷扰动发生5 s 后,风电机组转速恢复控制启动,恢复过程持续时间TREC为35 s。系统频率死区设置为49.9~50.1 Hz,系统频率变化率的阈值δf取0.2%。
3.2 实验结果
3.2.1 未引入虚拟惯量控制
未引入虚拟惯量控制时,风电机组工作在MPPT 控制方式下,系统的响应特性曲线如图11所示。


图11 未引入虚拟惯量控制时系统响应特性曲线
图11中,当系统遭受较大负荷功率扰动时,由于两台模拟D-PMSG 机组均未引入虚拟惯量控制,在恒风速条件下机组的转速和输出功率基本保持不变,机组不响应系统频率的变化。此时系统调频负担完全由模拟同步发电机承担,系统频率波动范围较大,其最低点达到48.92 Hz。
3.2.2 采用所提的实用虚拟惯量控制策略
图12为采用所提的实用虚拟惯量控制策略的响应特性。

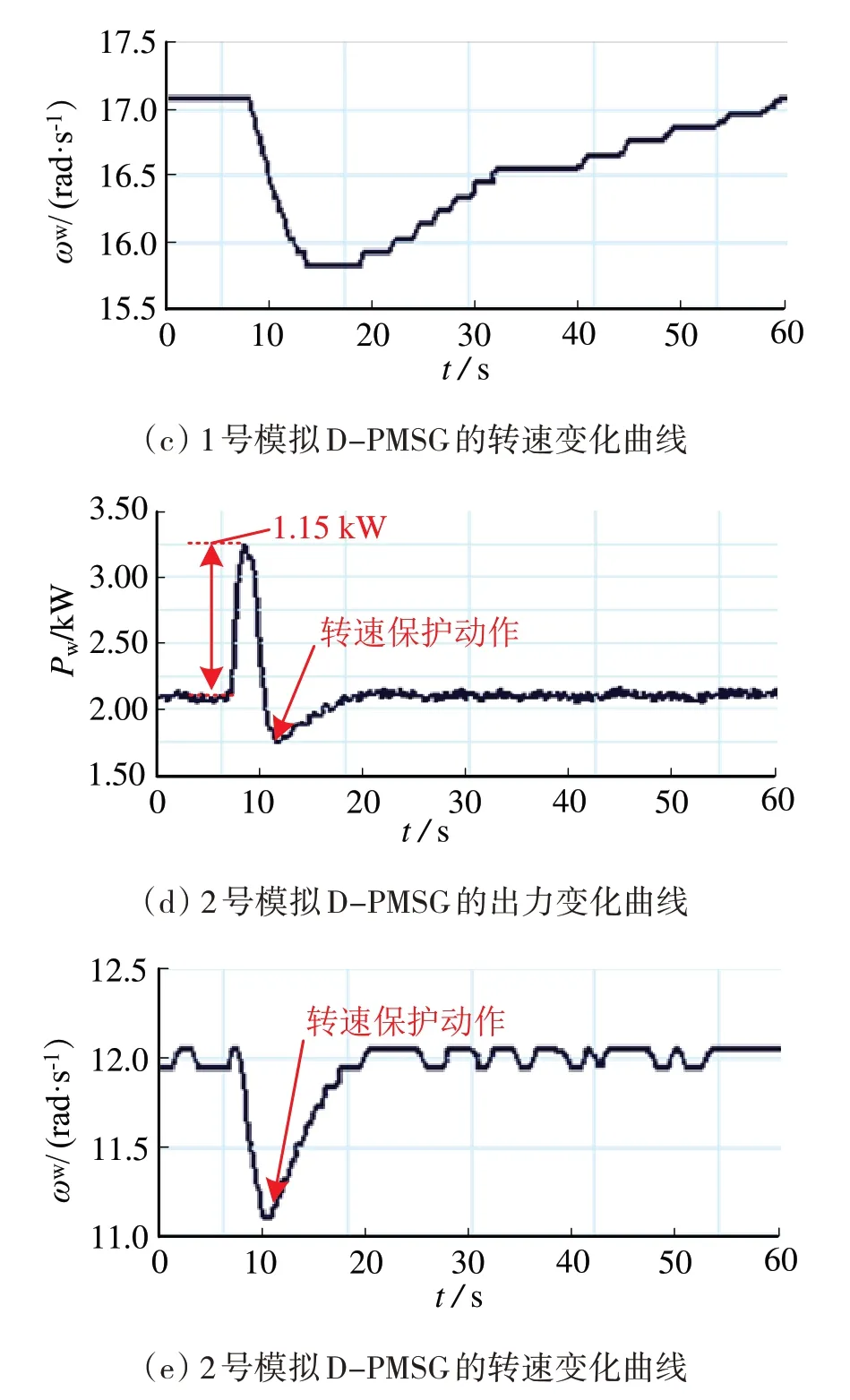
图12 采用所提虚拟惯量控制方法时的响应特性曲线
图12中,虚拟惯量控制的引入使得系统频率的最低点由48.92 Hz 提升到了49.33 Hz。调频过程中,1 号风机通过转速恢复控制的作用,风机转速能够自动恢复到MPPT 状态;2 号风机由于风速较低,参与调频过程中,当转速低于设定值时,在转速保护的作用下能够及时退出频率控制。
通过以上实验测试结果可见,所提的实用虚拟惯量控制方法在实际的风电换流器控制系统中实现时,风电机组能够正确检测系统频率扰动情况,有效参与系统调频,参与调频过程中,当风机转速较低时,风机转速保护能够及时动作,从而避免风机因转速过低引起停机。参与调频过程后,风机转速能够正常恢复到MPPT 控制工作点,从而保证风机的发电效率。
4 结论
为实现风电PD 虚拟惯量控制在实际风电机组中的应用,针对风电机组参与电网调频存在的特点和限制,基于已有的PD 虚拟惯量控制方法,提出了一种实用的风电虚拟惯量控制方法,并给出了该方法的具体执行步骤。所提方法从频率事件检测、风机转速保护、风机转速恢复三个方面对已有PD 虚拟惯量控制方法进行了优化,使风电机组在正确响应的频率扰动后能够及时恢复到最优转速运行,从而提高风电机组的发电效率,并为下一次调频控制做好准备。本文通过仿真分析和实验测试,验证了所提方法在实际风机中应用的可行性。
