混沌双算子亨利溶解度算法的瓦斯涌出量预测模型∗

付 华，刘 昊，徐耀松，赵俊程，许 桐

(辽宁工程技术大学电气与控制工程学院，辽宁省 葫芦岛 125105)

煤矿井下开采过程中，煤壁缝隙会涌出瓦斯气体，过快或过量的瓦斯涌出会引发瓦斯爆炸、煤与瓦斯突出等事故，对瓦斯涌出量的精准预测是防治煤矿瓦斯事故的重要措施[1]。

近年来，国内外许多学者利用瓦斯涌出密切相关的易测过程变量和机器学习算法建立预测模型，有效地提升了对瓦斯涌出的防治能力。Yang 等[2]构建了一种改进的灰色GM(1，1)和RBF 神经网络相结合的瓦斯涌出量预测模型；刘鹏等[3]融合支持向量机和决策树算法提出一种增强决策树回归算法，并应用于瓦斯涌出量的预测。上述研究没有对所用算法的参数进行优化，在一定程度上限制了预测精度。任志玲等[4]采用遗传模拟退火算法优化回归型支持向量机的参数，建立了瓦斯涌出量的非线性回归拟合模型；徐耀松等[5]提出一种改进的万有引力算法，用于搜索更优的BP 神经网络的初始权值和阈值，提高了瓦斯涌出量预测模型的精度和收敛速度；董晓雷等[6]采用遗传算法优化SVM 的关键参数，对回采工作面瓦斯涌出量进行预测；温廷新等[7]提出了融合BP 神经网络、PSO 算法和AdaBoost 算法的瓦斯涌出量的分源预测模型。上述学者利用智能优化算法对预测模型的关键参数进行优化，有效提升了预测的精准度。但瓦斯涌出不是简单的静态过程，影响因素众多且信息堆叠，有必要经过预处理以进一步提高数据驱动预测模型的效率和精度。皮子坤等[8]使用主成分分析方法进行降维，建立了改进果蝇算法优化GRNN 的预测模型。但主成分分析更适用于线性数据，对于存在复杂非线性关系的瓦斯涌出量相关因素数据[9]，采用非线性降维方法更合理高效。肖鹏等[10]通过改进的遗传算法优化BP 神经网络的参数，经核主成分分析(Kernel Principal Component Analysis，KPCA)维数约简后的瓦斯涌出量相关数据作为输入变量，所构建的耦合算法预测模型表现出较好的泛化能力和预测精度。

最小二乘支持向量机对于非线性小样本问题具有优秀的求解精度[11]，相比神经网络更适用于瓦斯涌出量的预测建模，但其预测能力受惩罚参数和核参数配置的影响较大。亨利溶解度优化算法(Henry Gas Solubility Optimization，HGSO)具有全局寻优能力强、需调节参数少等特点，已成功应用于多类实际优化问题[12]。因此，将融合Tent 混沌映射和哈里斯鹰算法(Harris Hawk Optimization，HHO)的改进亨利溶解度算法(Improved Henry Gas Solubility Optimization，IHGSO)用于优化最小二乘支持向量机(Least Squares Support Vector Machines，LSSVM)的关键参数，建立煤矿井下回采工作面的瓦斯涌出量动态预测模型。为降低瓦斯涌出量影响因素数据间相关性的影响，提高模型的运算效率，使用KPCA 对选取的瓦斯涌出量影响因素进行特征提取。

1 瓦斯涌出量影响因素的选取与数据降维

1.1 瓦斯涌出影响因素的选取

瓦斯涌出是煤体或岩层破裂向采掘空间释放瓦斯的动态过程。瓦斯在煤层中的赋存状态随矿井开采区域地质条件和采掘情况的变化而动态变化，煤层厚度和深度等地质因素决定着煤层瓦斯含量和分布情况，开采规模、开采顺序和采掘工艺等开采因素影响着瓦斯涌出的速率。

瓦斯涌出量的影响因素具有强耦合性、高度非线性和随机性等特征[13]，煤层中的瓦斯含量作为瓦斯涌出量最主要的影响指标，两者之间的关系可以利用下式表示，

式中:q1表示排放时间内单位暴露面积上的瓦斯量；q0表示在排放时间内的平均瓦斯量；a为瓦斯含量系数，可根据w＝求得；w表示瓦斯含量；p表示瓦斯压力；re为钻孔半径；m为煤层厚度。由式(1)可以确定煤层瓦斯含量与瓦斯涌出量呈正相关关系。

瓦斯涌出过程可由多种影响因素从不同的角度表征，选取多个影响因素可以弥补不同检测手段的不足。因此，根据回采工作面瓦斯涌出特性和影响因素的分析以及有关研究[14]，结合矿区的实际情况，从地质因素和开采技术角度出发选取瓦斯涌出量指标变量，并从时间角度将其划分为动态和静态变量。动态辅助变量包括开采层瓦斯含量、临近层瓦斯含量、推进速度、采出率、日产量；静态辅助变量包括煤层深度、煤层厚度、煤层倾角、煤层间距、采高、邻近层厚度、层间岩性、工作面长度，将其中13个指标作为瓦斯涌出量预测模型的辅助变量。

1.2 瓦斯涌出量影响因素数据的降维

运用KPCA 算法提取出低维瓦斯涌出量主成分影响因子代替高维初始影响因子，实现对预测模型效率的提升。瓦斯涌出的相关因素数据共同构成数据集D＝[D1D2…Dp]T，其中，p为选取瓦斯涌出量影响因素的种类数目。为减少量纲对预测指标的影响，首先对D进行标准化处理得到D′。

式中:i，j＝1，2，…，m，m为数据集样本数量。通过映射函数将D′映射到高维空间，即:

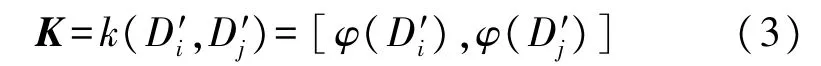
式中:φ为非线性映射函数。将K中心化得到，通过对其协方差矩阵特征分解[15]，计算得的n个特征值λ和特征向量μ。选取前q个较大的特征值，对这q个特征值及其对应的特征向量计算得到特征提取后的瓦斯涌出量影响因素主成分数据集Z，即预测模型的输入参量，

2 混沌双算子亨利溶解度算法

标准亨利溶解度算法中的初始个体都是在搜索空间内随机生成的，迭代过程中在集群内逐渐靠拢；最差个体以随机更新的方式带领种群跳出局部空间，但在一定程度上削弱了算法在局部空间的开发能力；而且只有一种位置更新策略，导致算法难以实现全局遍历搜索和局部开发之间的平衡和适时切换。因此，将Tent 混沌映射引入种群初始化过程，利用概率转换参数实现搜索策略的自适应变换，增强算法的寻优性能。

2.1 种群初始化过程

利用混沌变量的随机性、遍历性和规律性的特性在初始解空间内进行优化搜索，生成分布性更好的初始种群。Tent 混沌映射相比其他混沌映射具有更好的遍历性和更快的搜索速度[16]，Tent 混沌映射的表达式如下:

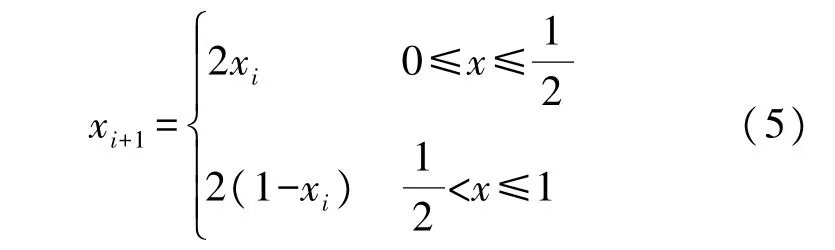
将混沌序列分量转换到对应解空间内:

2.2 迭代寻优过程

随着IHGSO 的寻优迭代，IHGSO 通过概率转换参数自适应地选择HGSO 算子或HHO 算子，进而实现IHGSO 在全局和局部空间内搜索策略的转换[17]。概率转换参数E的公式如下:

式中:t为当前迭代次数，T为最大迭代次数，E0为(－1，1)的随机值。由式(7)可以看出，概率转换参数E的选取考虑了随机性和迭代次数的作用，其值是随着迭代过程动态变化的。在算法迭代初期，t值较小，E的绝对值大于1，算法自适应地选择HGSO 算子执行全局探索过程索；随着寻优过程的推进，t值越来接近T，E的绝对值逐渐小于1，算法自适应地选择HHO 算子执行局部开采过程。设R为逃脱系数，是在0 到1 间的随机数，则IHGSO 在局部领域内寻优LSSVM 最佳关键参数的过程为:

①当R≥0.5 且｜E｜≥0.5 时，执行软围攻策略靠近关键参数最优解，数学表达式为:

式中:Δx(t)表示第t次迭代最优个体与当前个体的差值，J＝2(1－R)。

②当R≥0.5 且｜E｜<0.5 时，执行硬围攻策略靠近关键参数最优解，公式如下:

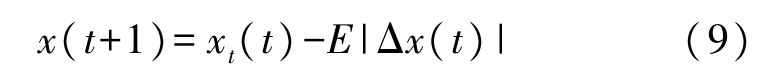
③当R<0.5 且｜E｜≥0.5 时，执行渐进式软围攻策略靠近关键参数最优解，迭代公式如下:

式中:D表示问题维度；S为D维随机向量；LF 为Levy 飞行函数；u和v为(0，1)均匀分布的随机数；τ＝1.5。

④当R<0.5 且｜E｜<0.5 时，执行渐进式硬围攻策略靠近关键参数最优解，如式(13):

2.3 性能测试与分析

2.3.1 测试函数选取

为了验证IHGSO 的优化性能和稳定性，选用10个单峰、多峰和固定维数基准测试函数进行寻优对比测试。测试函数的具体信息如表1 所示。

2.3.2 实验参数设置

选取亨利气体溶解度算法、哈里斯鹰算法、海洋捕食者算法[18](Marine Predators Algorithm，MPA)、鲸鱼优化算法[19](Whale Optimization Algorithm，WOA)、粒子群算法[20](Particle Swarm Optimization，PSO)、灰狼优化算法[21](Grey Wolf Optimizer，GWO)、麻雀搜索算法[22](Sparrow Search Algorithm，SSA)和改进算法进行对比，所有算法的共有参数保持一致，种群规模设置为50，最大迭代次数设置为1 000，维数取值如表1 所示。各算法参数的详细设置如表2 所示。

表1 测试函数

表2 各算法的参数设置

2.3.3 实验结果及分析

为了去除偶然性引起的误差，通过MATLAB 分别对10 个标准测试函数进行30 次独立试验。表3列出了上述8 种算法对单峰(F1－F5)、多峰(F6－F8)和固定维数(F9－F10)测试函数得到的实验结果。

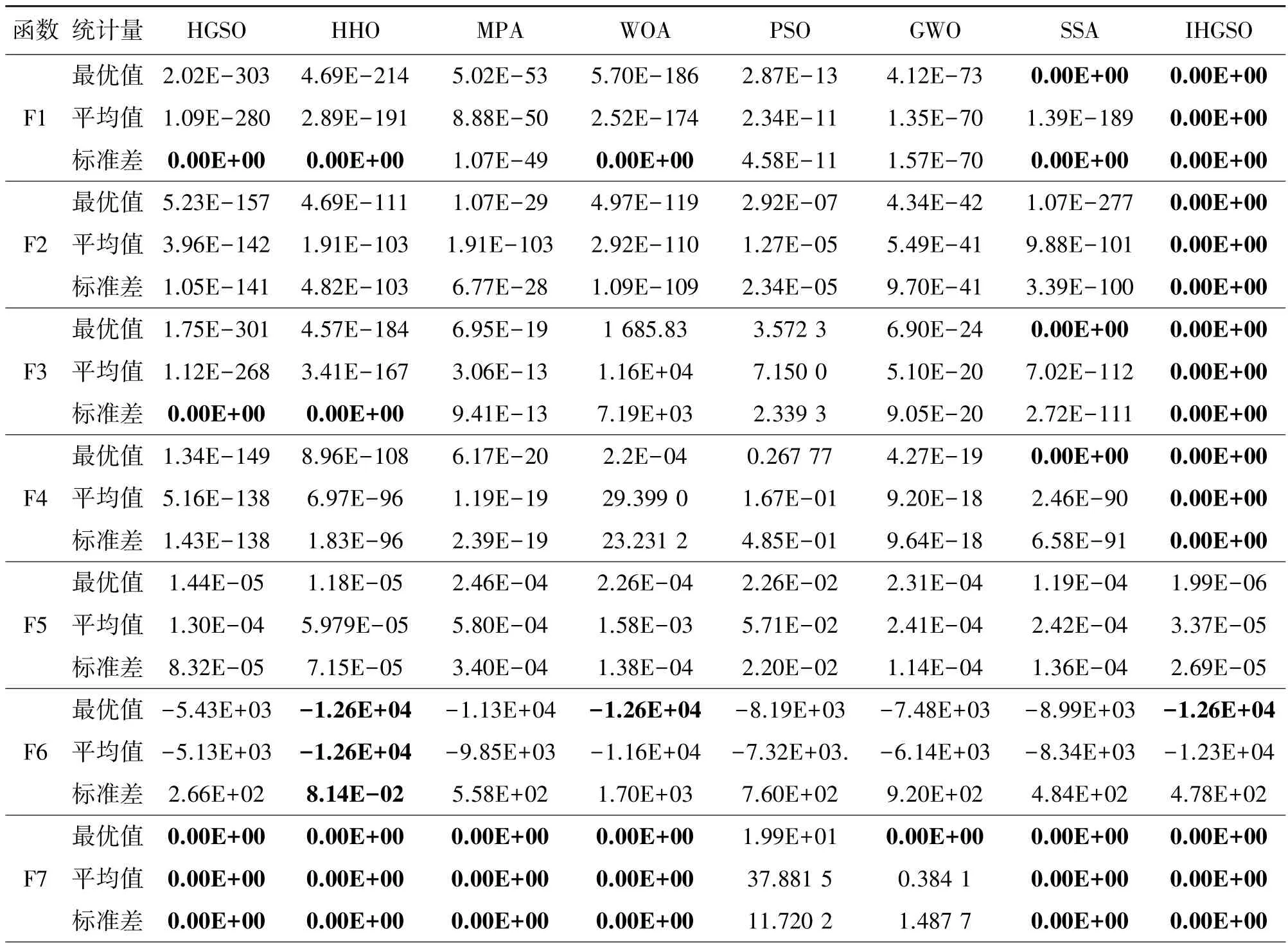
表3 测试函数寻优结果

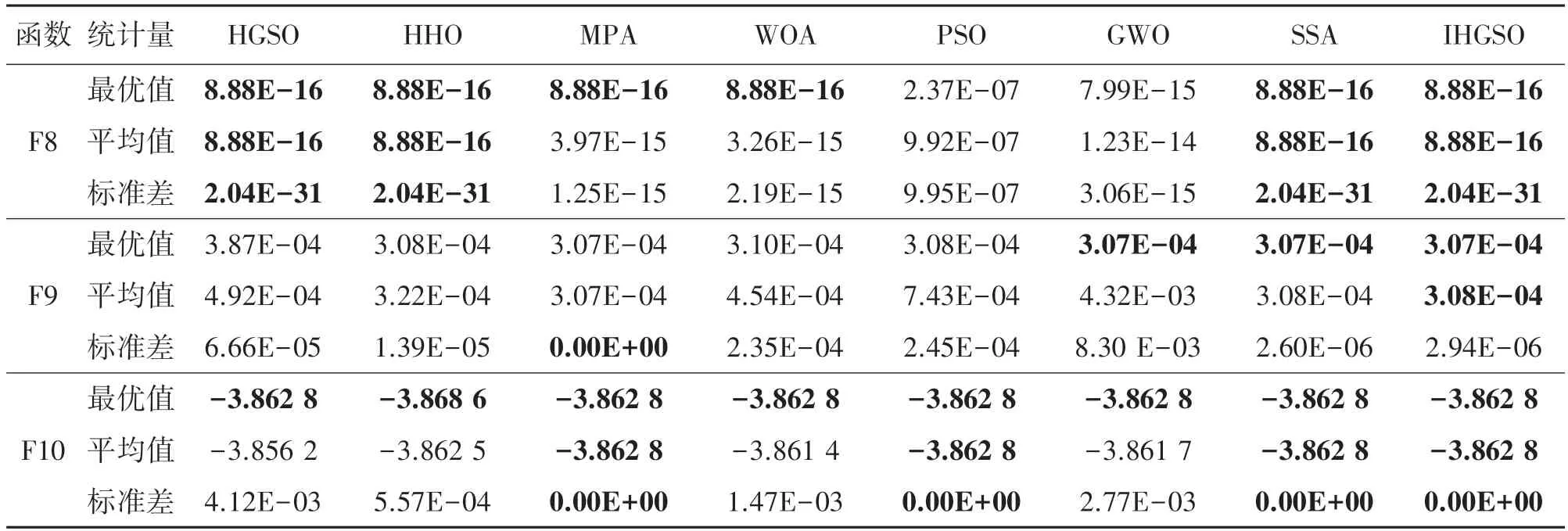
续表3 测试函数寻优结果

在相同的约束条件下，对于单峰函数F1、F3 和F4，SSA 和IHGSO 能找到其理论最优解0，但SSA的平均寻优结果不如IHGSO，IHGSO 对比其他算法在标准差上的表现优异；对于单峰函数F2，只有IHGSO 算法经过迭代搜寻到理论最优值，并且平均值和标准差都为0；对于单峰函数F8，虽然IHGSO没有寻找到其理论最优解，但是三个评价指标都优于其他算法。在对5 个单峰函数的多次寻优测试中，IHGSO 各评价指标均为最优，说明IHGSO 具有优秀的局部寻优能力和稳定性。对于多峰函数F6，HHO、WOA 和IHGSO 都能够寻找到最优值，但HHO 的30 次寻优结果的平均值和标准差更加优秀，证明了HHO 良好的局部极值逃逸能力；对于多峰函数F7 和F8，HGSO、HHO、WOA、SSA 和IHGSO在对其多次寻优得到的结果基本都为理论最优值，IHGSO 表现出优秀的收敛精度和稳定度。在对固定维数测试函数的寻优中，几种算法寻找到的最优解基本一致，都能收敛到理论最优解附近。但在平均值和标准差上，IHGSO 优于其他对比算法几个至十几个数量级，展现出更优秀稳定的寻优效果。

通过基准测试函数迭代收敛曲线的绘制进一步直观地对比各个算法的收敛性和跳出局部空间的能力，选取测试中与结果平均值相近的一次绘制各算法的迭代收敛曲线，其中横轴表示迭代数，纵轴表示适应度值的对数。由图1 可知，对于不同类型的测试函数，在几种算法收敛到相同精度的情况下，IHSGO 所需的迭代次数最少，证明改进策略能有效提升算法的收敛速度。随着迭代次数的增加，其他几种算法均出现不同程度的停滞，IHGSO 收敛曲线阶梯波动式下降表明IHGSO 能够脱离局部最优停滞。

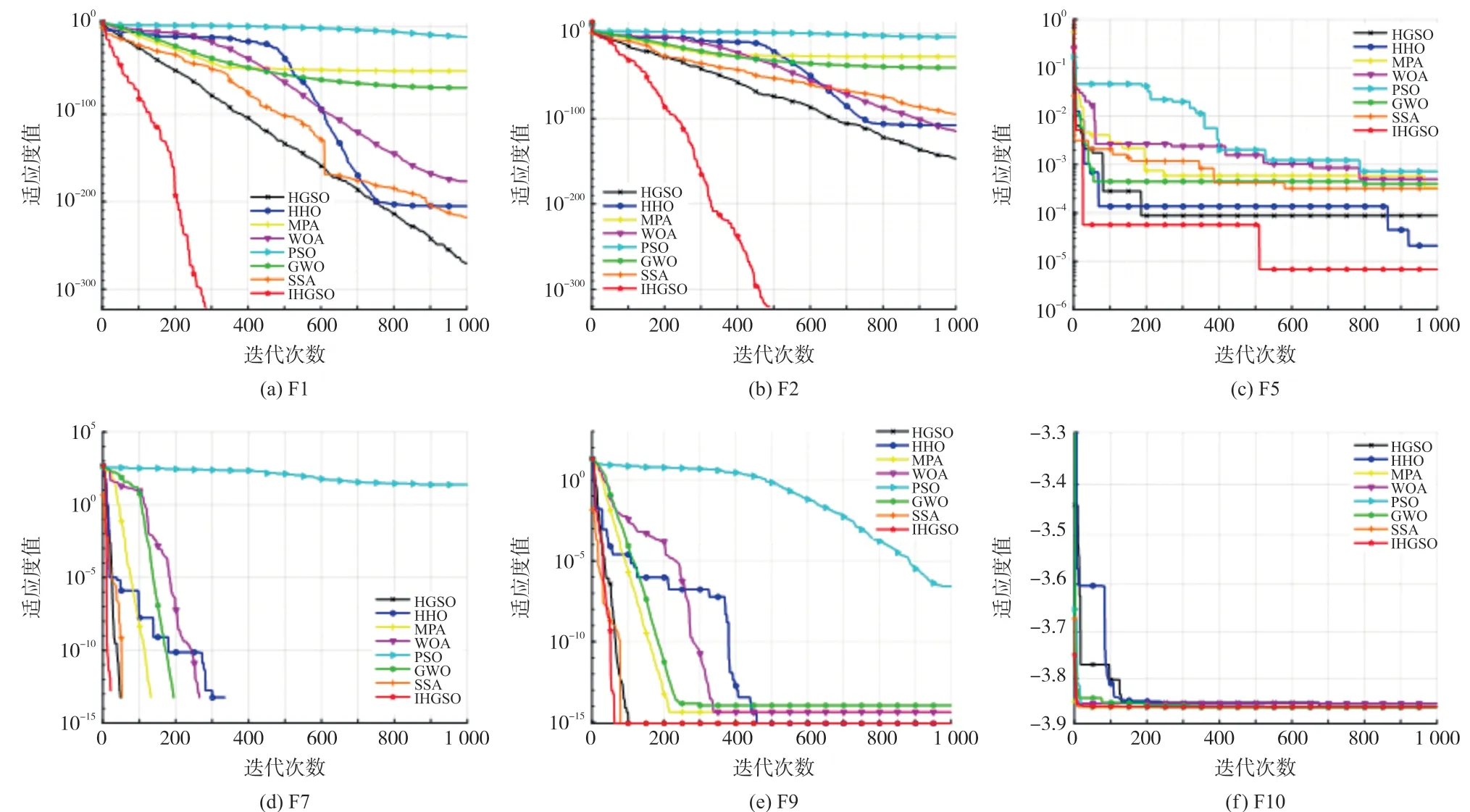
图1 部分函数收敛曲线

综上可知，IHGSO 在对不同测试函数的寻优中，相比于其他算法不仅寻优精度高，寻优稳定性方面也优势明显，证明了改进策略的有效性和改进算法的优越性。

3 煤岩瓦斯涌出量预测模型的模型的构建

3.1 瓦斯涌出量LSSVM 预测算法

将瓦斯涌出量影响因素维数约简至q维的主元数据Z＝[Z1Z2…Zq]T作为LSSVM 预测模型的输入参量，对瓦斯涌出量Y进行预测。LSSVM 的目标优化函数和约束条件如下式:

式中:J(·)表示目标函数，φ(·)表示非线性函数，c表示惩罚因子，ξ表示误差变量，ω表示法向量，b表示偏置量。

经过训练得到的瓦斯涌出量LSSVM 模型回归函数为:

式中:K(zi，zj)表示径向基核函数，g表示核函数宽度。

瓦斯涌出量LSSVM 预测模型中有2 个待优化参数，即惩罚系数c和核函数参数g，这两个参数的选取直接关系到模型的抗干扰能力和泛化能力。利用改进的亨利溶解度优化算法调整LSSVM 的关键参数，从而得到煤矿井下瓦斯涌出量IHGSO-LSSVM预测模型。

3.2 瓦斯涌出量IHGSO-LSSVM 预测步骤

①IHGSO 参数初始化。设置种群规模、迭代次数等参数，在搜索空间内随机选取初始种群，然后经过Tent 混沌搜索得到混沌种群；

②确定LSSVM 参数c和g的范围，c∈(0，100]，g∈(0，100]；

③IHGSO 根据概率转换参数自适应地选择搜索策略，通过个体迭代更新不断靠近LSSVM 关键参数最优解，并更新迭代次数t；

④将瓦斯涌出影响因素特征提取后的主成分数据作为模型的输入，从而进行模型训练。将模型的输出值和真实值之间的均方根误差作为适应度函数来度量模型的偏差情况，适应度最优时作为最优解，

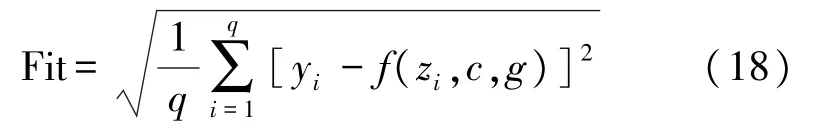
⑤判断是否满足终止条件:t≥T，若满足则继续执行步骤⑥，否则返回步骤③；

⑥输出最优解，即LSSVM 模型的核函数参数值和惩罚参数值，利用该优化后的参数训练LSSVM 模型，即完成IHGSO 优化LSSVM 的瓦斯涌出量预测模型的建立。

4 实验测试与分析

4.1 瓦斯涌出量影响因素预处理

实验数据选自某矿井工作面的历史监测数据，筛选出30 组实测数据作为研究对象，并从中选取21 组数据作为训练样本，剩余数据作为测试样本。部分瓦斯涌出量影响因素数据如表4 所示。

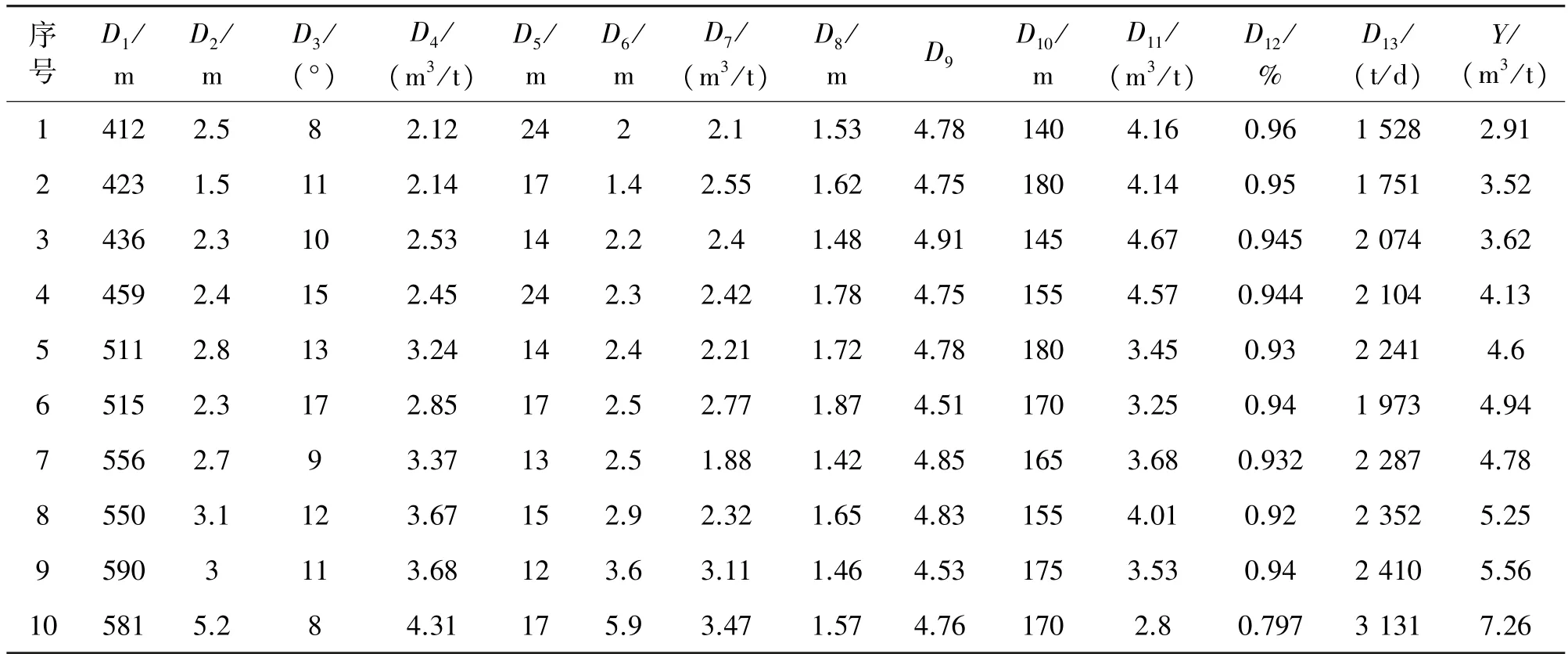
表4 部分瓦斯涌出量影响因素数据

对十三类瓦斯涌出量预测指标进行核主成分分析，得出各主成分排序后的方差贡献度并计算累计方差贡献度，如图2 所示。

从图2 中可以看出，前3 个主元的累计方差贡献率为87.09%，表明这3 个主元能够实现所有主元表达能力的85% 以上。因此，在原始的13 个特征指标提取3 个主成分作为瓦斯涌出量预测模型的输入变量。

图2 各成分贡献占比图

4.2 瓦斯涌出量IHGSO-LSSVM 模型结果

将KPCA 预处理后的瓦斯涌出相关因素主成分数据作为输入，对IHGSO-LSSVM 预测模型进行仿真实验，结果如表5 所示。IHGSO-LSSVM 预测模型的最小误差为0.036 3，最大误差为0.198 7，测量结果的误差均在0.2 m3/min 以内，说明该模型具有较好的拟合精度。

表5 IHGSO-LSSVM 预测模型结果

经过多次训练得到改进的亨利溶解度算法优化LSSVM 的最优适应度，如图3 所示。

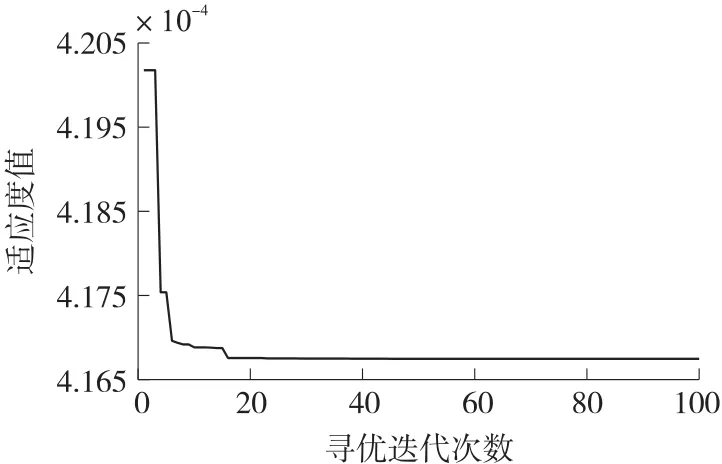
图3 适应度值曲线图

由图3 可知，IHGSO 优化算法在迭代前期能够快速收敛，且具有优秀的寻优精度。当迭代次数接近20 时，样本的均方误差就可以到达最优状态，得到的寻优参数分别为:c＝5.24，g＝2.23。

4.3 不同模型误差对比

为进一步验证瓦斯涌出量IHGSO-LSSVM 预测模型的性能，将其与ELM(Extreme Learning Machine，ELM)模型、LSSVM 模型、PSO-LSSVM 模型和SSALSSVM 模型和对比，比较测试样本的预测结果。为保证实验的客观性与一般性，对各模型进行多次实验取平均值。其中，IHGSO、PSO 和SSA 参数设置如表2 所示，种群规模和迭代次数分别设置为30 和100。图4 为5 种模型在测试样本下得到的瓦斯涌出量预测值和实际值的对比曲线，图4 中IHGSOLSSVM 预测模型效果更好，拟合精度更高。

图4 不同预测模型结果

通过均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)三种评价指标，对比分析不同模型的测量性能。三种评价指标的数学表达为:

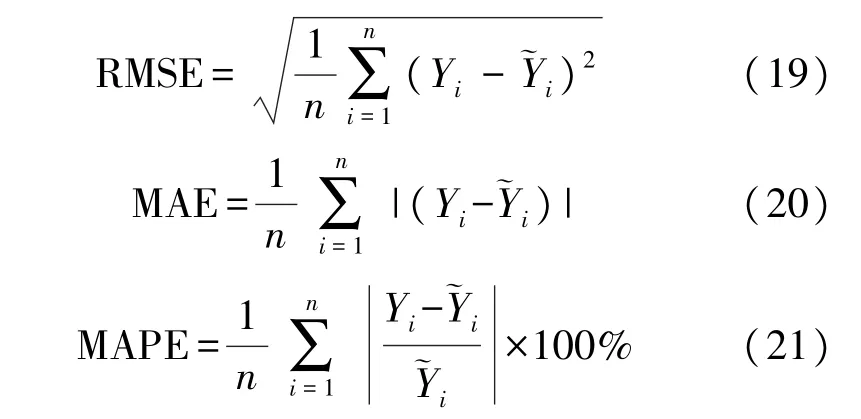
式中:n为测试集样本个数，Yi为预测值，为实际值。三种误差RMSE、MAE 与MAPE 的值越小，代表预测的精度越高，即模型的效果越好。表6 为5 种预测模型预处理前后的误差对比。

由表6 可得，经核主成分分析非线性约简后的多种模型在整体上预测准确率呈不同程度的提升，运行时间也较未经预处理有所减少。经特征提取处理后的ELM、LSSVM、PSO-LSSVM、SSA-LSSVM 和IHGSO-LSSSVM 五种模型的平均绝对百分比误差分别为8.015 2%、14.465 0%、12.390 4%、3.041 1%和1.565 6%。经PSO、SSA 和IHGSO 优化后的LSSVM模型在预测精度上提升显著，运行时间虽有所增加但仍处在合理范围内。其中，IHGSO-LSSVM 模型在预处理前后都表现出优秀的预测性能，能够准确实时地对井下瓦斯涌出量进行预测，达到理想的预测效果。

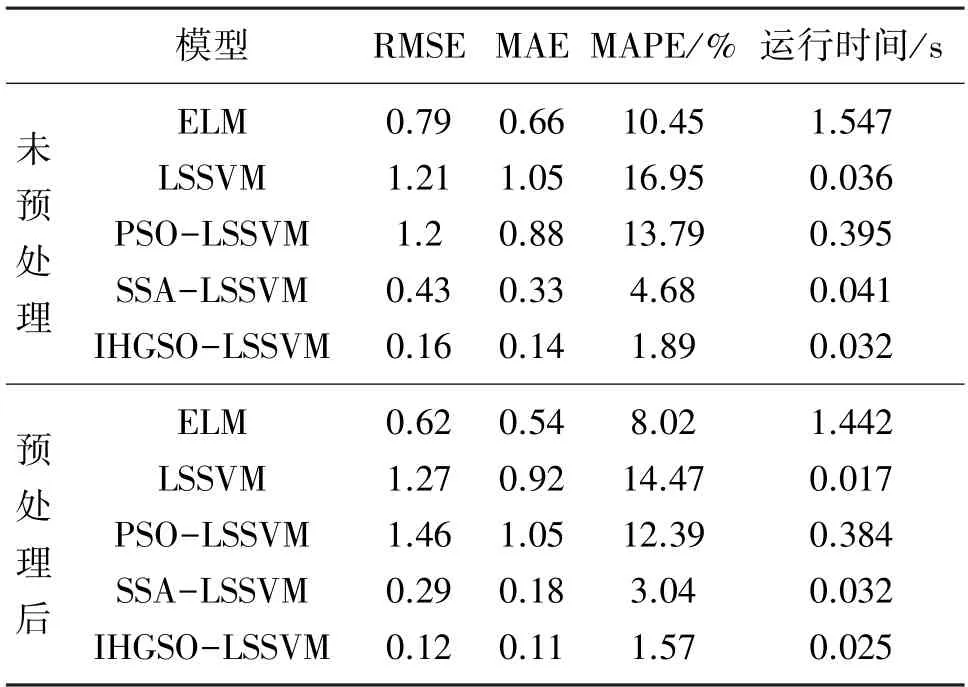
表6 不同预测模型结果误差对比

5 结论

本文提出了一种基于混沌双算子亨利溶解度算法优化LSSVM 的煤岩瓦斯涌出量预测模型。引入Tent 混沌映射和哈里斯鹰算子的改进亨利溶解度算法在基准函数寻优测试中，相较标准HGSO 综合性能显著提升，相比于其他算法具有更好的收敛性能和求解稳定性，验证了改进策略的有效性和改进算法的优越性。IHGSO 能够有效地对LSSVM 的惩罚因数和核函数参数进行优化，改善了LSSVM 对初始惩罚因数和核函数参数依赖。利用KPCA 进行瓦斯涌出特征的提取，降低了模型输入参量的维数。经KPCA 特征提取后的煤岩瓦斯涌出量预测模型的均方根误差和平均绝对误差可缩小至0.156 4 和0.133 2，平均绝对百分比误差为1.565 6%，运行时间仅为0.024 9 s，比其他预测模型具有更好的表现。