基于遥感数据和表层声速的全海深声速剖面反演

李倩倩，李宏琳，曹守莲，严娴，马志川

(1.山东科技大学 测绘与空间信息学院，山东 青岛 266590；2.哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨 150001)

1 引言

海水声速是海洋环境观测的基本要素之一，对于水下声波定位与目标探测、海洋环境监测和资源勘探等一系列活动至关重要[1–2]。获取声速剖面最直接的方法是现场观测，但此类方法费时费力，且由于声速的时空变化特性，这些现场观测资料都不能获得大范围实时声速剖面。随着时间推移，海洋垂向观测资料（船只走航、站点观测、潜标、水下滑翔机和浮标等）日益增多，特别是中国Argo 实时资料中心[3]提供的大量观测剖面以及网格产品，在海洋科学研究和应用中发挥了重要作用。然而，现有垂向观测资料的空间分辨率仍然较低，且不能实时地描述海洋内部的结构变化特征。而另一方面，随着遥感卫星传感器的不断发展，海面温度和海面高度等资料逐渐完善，它们能实时地提供海面信息且具有较高的空间分辨率。但通过遥感卫星资料得到的信息仅仅停留在海洋表层或者近表层，无法获得海表面以下的信息。因此，利用遥感卫星观测数据和Argo 剖面数据相结合的方式来反演海洋声速剖面成为重要的研究课题。

理论上，声速剖面可以表示为深度和时间的矩阵形式，然而，该表示形式需要大量参数，不利于声速剖面的反演估计，为此Tolstoy 等[4]提出了经验正交函数（EOF）的表示方法。从而声速剖面可以利用有限几阶EOF 系数进行表示，声速剖面的反演问题最终变为EOF 系数的反演[5–6]。自20 世纪80 年代以来，世界各国海洋学家提出将海面信息映射到海洋内部，从而反演温度、盐度剖面。早期，Hurlburt 等[7]通过考虑水动力和能量交换特征，构建数值海洋预测模型，将模拟的高度计数据动态传递到海洋内部得到模拟数据对温跃层的敏感性。Carnes 等[8–9]在墨西哥湾流区域发现了关于海面高度、海面温度与海洋标准层之间的统计关系，随后，他们对西北太平洋和西北大西洋的温度剖面进行EOF 分解，建立海面数据与温度剖面的回归关系，即单经验正交函数回归（single Empirical Orthogonal Function regression，sEOF-r）方法。该方法已被美国海军海洋预报系统[10]采用。Chen 等[11]利用海面数据结合sEOF-r 方法重构了全球范围的声速剖面，并证明声速误差与动态漩涡活动相关。

近年来，人工神经网络（Artificial Neural Networks，ANN）在海洋环境参数反演估计中的应用越来越多。Liu 等[12–13]首次提出将自组织映射（Self-Organizing Map，SOM）神经网络应用在气象与海洋方面，发现自组织映射神经网络可以从联合高频雷达和声学多普勒流速剖面仪（ADCP）数据集中提取非均匀的、各向异性的三维沿海海洋流场变化。Charantonis 等[14]，Chapman 和Charantonis[15]使用自组织映射方法逐步重建高度相关的海洋滑翔机稀疏数据集中的缺失数据（温度、盐度剖面）。随后进一步提出基于数据空间局部相关性改进的SOM 神经网络新方法，根据卫星提供的海洋表面信息以及Argo 浮标测量的深海海流速度提高深海洋流的重构速度精度。Chen 等[16–17]利用SOM 神经网络建立了温度剖面对应的经验正交系数与西北太平洋海表面等多维信息的自组织特征映射图，从而获取待反演的系数并有效地重构了1 000 m 以内的温度剖面。Jain 和Ali[18]采用人工神经网络的方法根据海表面参数以及温、盐剖面直接反演250 m 深度的声速剖面。与传统线性反演方法相比，神经网络等非线性方法可以捕捉海表面数据与声速剖面异常之间的非线性关系，从而提高反演精度。

为此本文在前人研究的基础上，利用人工神经网络的方法根据遥感卫星观测数据和Argo 历史数据建立局域时空海洋声速场。即利用中国Argo 实时资料中心提供的历史声速剖面生成EOF 基函数与系数，联合实时测量的海面遥感数据和表层声速仪测量的固定深度处数据，利用SOM 神经网络实现对全海深声速剖面的实时反演。

2 数据与方法

2.1 数据来源

本文所使用的温度、盐度剖面数据来自中国Argo实时资料中心提供的全球海洋Argo 网格数据集[3]。其时间覆盖范围为2004 年1 月至2020 年12 月，空间分辨率为水平1°×1°，垂向标准层共有58 层（0～1 975 m）的逐年逐月网格化资料。

卫星遥感数据主要包括海表面温度（Sea Surface Temperature，SST）数据和海平面高度异常（Sea Level Anomaly，SLA）数据产品。SST 产品来源于美国国家海洋和大气管理局（Nation Oceanic and Atmospheric Administration，NOAA）的每日最优插值SST（Optimum Interpolation Sea Surface Temperature，OISST）[19]。该数据集将来自不同观测平台（卫星、船舶和浮标）的数据构建在一个常规全球网格上，其空间分辨率为0.25°×0.25°。SLA 数据为海面高度减去长时间序列的平均海面高度，其来自于卫星海洋数据存储、验证、插值处理中心（Archivings Validation and Interpretation of Satellite Oceanographic，AVISO）提供的0.25°×0.25°的月平均网格数据，该数据融合了TOPEX/POSEIDON、JASON-1/2 和ERS 等多颗卫星的测高资料[20]。

2.2 数据时空匹配

本文选取东南印度洋（14.5°～17.5°S，85.5°～90.5°E）范围为研究区域，海表面遥感数据对应截取14.375°～17.625°S，85.375°～90.625°E 之间的数据。如图1 所示，蓝色圆点表示海表面遥感数据所在位置，红色圆点表示Argo 数据所在位置。图1 表明，遥感数据与Argo 数据在经度、纬度方向都相差0.125°，即Argo数据格点和海表面数据格点之间存在空间不匹配的问题。本文通过对Argo 数据点周围的4 个海表面数据取算数平均，将遥感数据降采样为1°×1°。从而保证SST 和SLA 数据与Argo 数据在水平方向上的采样位置一致。同时，海表面数据中的SST 是日平均数据，与SLA 和Argo 的月平均数据在时间上不匹配，因此本文将SST 数据按月进行算数平均，从而实现3 组数据在时间采样上的一致性。

2.3 构建声速剖面EOF 函数

利用EOF 方法表示声速剖面可以大大降低声速剖面反演所需要的参数个数，基函数确定后，利用有限的几阶系数即可表示声速剖面。假如某测区内有N条实测声速剖面，将其插值到M个深度标准层，从而声速剖面可以表示为矩阵CM×N

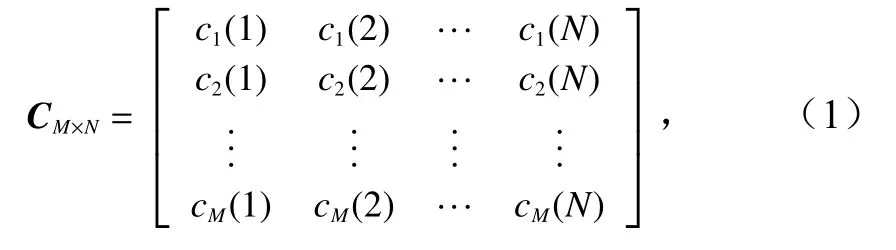
式中，每一列代表一个声速剖面，每一行代表N条剖面在同一深度处的声速。

对式（1）中每行取平均，获得平均声速CM×1，声速剖面矩阵与平均声速矩阵之间的差值称为声速扰动∆CM×N，求声速扰动的协方差矩阵COVM×M

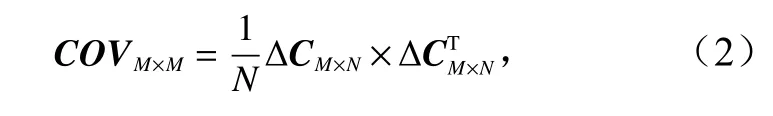
并对其进行特征分解得：

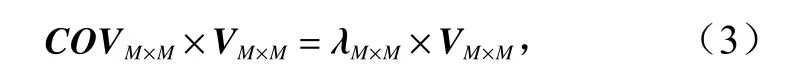
式中，λM×M为特征值矩阵；VM×M是特征向量矩阵，即为EOF 基函数。

将EOF 投影到声速扰动 ∆CM×N，可得到：

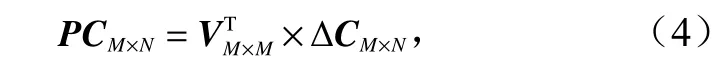
式中，PCM×N中的每一列为对应声速扰动剖面的EOF系数。

每一个特征向量对应的特征值表示此特征向量的权重，计算前k阶的贡献率为

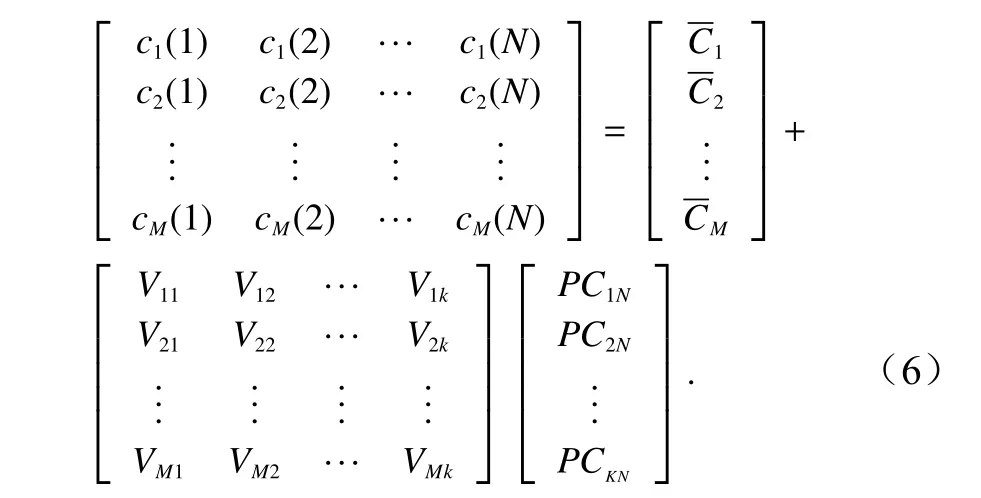
当Q≥0.95时，认为前k阶经验正交函数可以表示当前海域内声速剖面的主要特征。因此，前k阶经验正交函数即可重构样本中的任一声速剖面，其中N个重构声速剖面表示为

2.4 SOM 神经网络

SOM 是在1981 年由芬兰学者Kohonen[21]提出的一种无监督竞争式学习前馈型神经网络模型。SOM算法步骤如下：

（1）初始化神经网络。对输入层的输入变量与竞争层输出神经元的初始连接权值赋予一个较小的常数，一般在[0，1]之间。设置学习率初始值为（0，1）之间某一数值，初始化邻域函数，确定邻域半径及邻近神经元集合，该集合随着训练进行而减小。

（2）构建输入向量。输入层输入变量，对于输入层的X={x1,x2,···,xn}，X中各元素分别对应研究海域内声速剖面的EOF 系数、地理位置以及对应的SST、SLA 数据。首先对输入变量进行归一化处理，然后输入到网络。

（3）计算输入向量与神经元之间距离。对于每一个输入变量，计算出输入数据与所有的输出神经元j之间的欧式距离dj。计算公式如下：

式中，wi j为 输入层第i个神经元和输出层第j个神经元之间的权值。

（4）找出获胜神经元c。通过计算得到最小距离dj的神经元j，距离最小的神经元j，作为获胜神经元c或最佳匹配单元（Best Matching Unit，BMU）。

（5）确定获胜邻域Sn(t)。确定获胜神经元的邻域范围，邻域范围一般由邻域函数确定，本文的邻域函数H采用Gaussian 函数，函数形式如下：

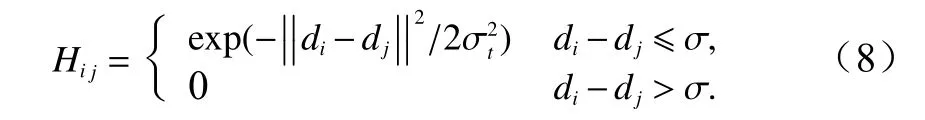
根据式（9）对获胜神经元c及邻域内的权值向量进行更新，使其向输入向量不断靠拢，

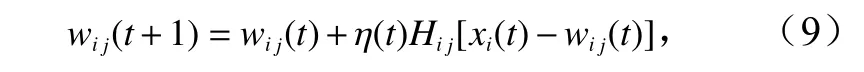
式中，wi j(t+1)为第t+1 次迭代过程中第j个节点的权重向量；H(t)为邻域函数；η(t)为学习速率。

（6）更新学习率以及邻域函数，学习率随着学习次数的增加而减小。

（7）重复步骤（3）和（4），直到完成所有输入数据的学习。

本实验中，根据Liu 等[12]提出的一种基于海面以下和现有数据之间相关性的距离度量函数，即式（11），计算已知信息与SOM 输出层单元之间的欧氏距离，通过寻找SOM 输出层中最佳匹配单元得到参考向量，将输入数据匹配到最佳单元来实现。

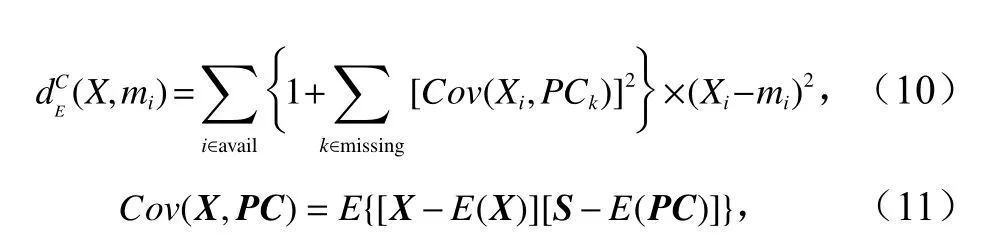
为了验证反演方法的精度，利用均方根误差（Root Mean Squar Error,RMSE）来表示声速剖面估计值与测量值之间的误差，定义均方根误差为

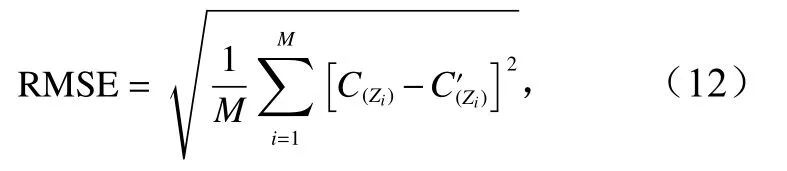
式中，M为深度点数；分别为测量和反演剖面在深度Zi处的声速值。

图2 给出了反演声速剖面的流程，具体步骤如下：

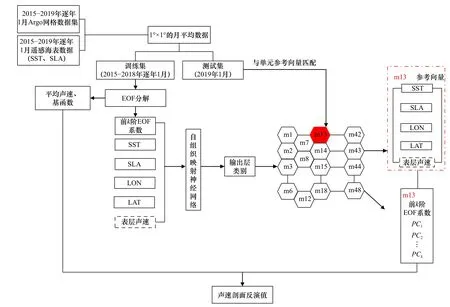
图2 声速剖面反演流程Fig.2 Flow of sound speed profile inversion

（1）将实验海域的声速剖面、海表面温度（SST）与海表面高度异常（SLA）数据分成训练集和测试集；

（2）对训练集的声速剖面进行EOF 分解，得到该区域的历史平均声速剖面、基函数以及系数PC（基函数在扰动矩阵上的投影）来表示训练集声速剖面；

（3）将步骤（2）中的系数与SST、SLA、纬度（LAT）、经度（LON）以及表层声速之间利用SOM 神经网络建立映射关系，通过验证集不断调整参数，得到最优训练模型；

（4）反演测试集EOF 的系数，将测试集的SST、SLA、LAT、LON 以及表层声速输入训练模型，计算与模型结果的最佳匹配单元（BMU），得到EOF 系数；

（5）将步骤（4）反演的EOF 系数结合步骤（2）的历史平均声速剖面和基函数得到声速剖面反演值。

3 实验数据处理及分析

从Argo 网格数据集中提取东南印度洋（14.5°～17.5°S，85.5°～90.5°E）范围内的月平均数据，利用该数据集中的深度、温度和盐度数据，通过Dell Grosso声速经验公式[22]计算声速剖面。利用上文提到的时空匹配方法，将海表遥感数据集和Argo网格数据集进行时空对准。将数据分为两部分，其中2015–2018 年逐年1 月的声速剖面和对应的SST、SLA 数据为训练集，主要用来生成声速剖面的平均值以及EOF 基函数，并且训练sEOF-r 和SOM 的模型参数。本文76 条声速剖面用于训练SOM，为了调整神经网络模型的超参数，20 条声速剖面作为验证集对模型的能力进行初步评估，测试集的24 条剖面用来评估模型的泛化能力。

3.1 EOF 基函数

该训练集中声速剖面的个数为N=76，深度上的分层数为M=1 976。图3a 的灰色细线为训练集中的声速剖面，黑色粗线为平均声速剖面。声速扰动如图3b 所示，最大值约为9 m/s，可以看出扰动主要位于水深400 m 以浅。图3c 为前6 阶EOF 的累计方差贡献率，可以看出，前5 阶EOF 的累积贡献率可达95.51%，已大于95%，所以此海域的海水声速剖面可用前5 阶EOF 近似表示。

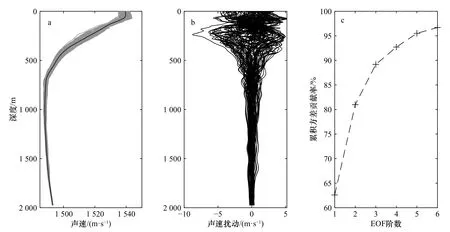
图3 训练集中的声速剖面（灰色线为实测剖面，黑色线为平均剖面）（a）、声速扰动（b）和前6 阶经验正交函数（EOF）的累积方差贡献率（c）Fig.3 The sound speed profile in the training set (gray lines are the measured profile,black line is the average profile) (a),residual sound speed (b) and the cumulative variance contribution rates of the first 6-order empirical orthogonal function (EOF) (c)

声速剖面反演精度主要取决于3 个方面：第一，训练集提取出的EOF 基函数是否具有代表性；第二，历史平均声速剖面是否具有代表性；第三，反演方法估计得到的EOF 系数是否准确。首先分析EOF 基函数的代表性，图4 为训练集和测试集前5 阶基函数之间的相关系数矩阵。该图表明，同组基函数相互正交，而测试集中的基函数与训练集中的基函数有明显差异，其中第1、3 阶表现为极强相关，第2 阶为中等程度相关，而第4、5 阶表现为极弱相关。

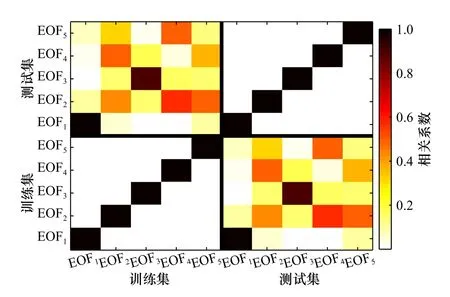
图4 训练集和测试集的经验正交函数基函数之间的相关系数Fig.4 Correlation coefficient between empirical orthogonal function (EOF) basis functions of training set and test set

图5 分别给出了训练集和测试集的前两阶基函数，测试集中前6 阶EOF 的累积贡献率以及训练集和测试集平均声速剖面的差值。图5a 表明，两组集合的第1 阶基函数非常相似，而第2 阶基函数的差异显著，尤其是在250 m 深度处，二者差异明显。图5b表明前2 阶基函数的累计方差贡献率就达到95.6%，其中第2 阶的累计方差贡献率为9%。以上分析表明，由测试集获取的基函数具有一定的代表性误差，其误差主要由第2 阶基函数造成，因此基函数的选取对声速剖面的反演很重要。图5c 是训练集与测试集平均声速剖面的差值，可以发现误差主要分布在上层，误差在2.66 m/s 之内。

图5 训练集和测试集的前两阶基函数（a）、测试集前6 阶经验正交函数（EOF）的累积方差贡献率（b）和训练集和测试集的平均声速误差（c）Fig.5 The first two order basis functions of the training set and the test set (a),the cumulative variance contribution rate of the first six orders of empirical orthogonal function (EOF) in the test set (b) and the average sound speed error of the training set and test set (c)

为了验证EOF 基函数和平均声速剖面的代表性误差对重构声速精度的影响，图6 利用训练集中提取出的基函数和平均声速剖面，通过最小二乘法对测试集中的声速剖面进行重构。图6 给出了利用前5 阶EOF 重构测试集的声速剖面与实际测试集声速剖面之间的绝对误差，误差范围为0～2.48 m/s。可以看出误差主要分布在400 m 以浅，即声速剧烈扰动的深度。图6 中的白色虚线为利用式（12）计算得到的声速剖面均方根误差，最大均方根误差约0.56 m/s。

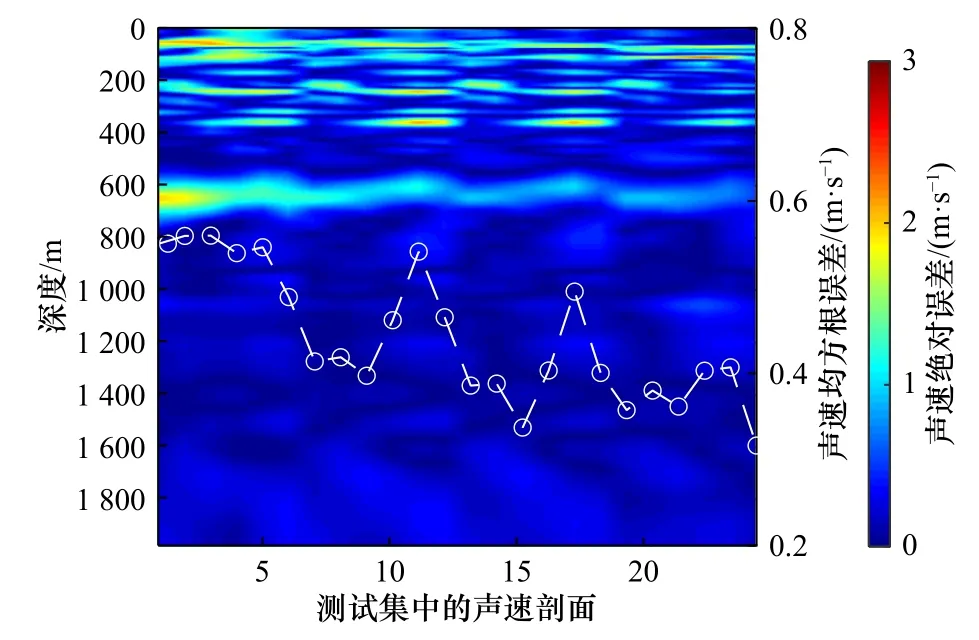
图6 声速剖面重构误差Fig.6 The reconstruction error of the sound speed profile

经验正交函数（EOF）是目前使用最广泛的声速剖面表示方法，EOF 方法对于一定数量的声速剖面在提取其主要特征时，获取的基函数比较准确，因此在这里暂不考虑EOF 基函数的代表性误差，历史平均声速剖面可以替换为现场观测的少数CTD 平均数据，这部分在文章后面会有讨论，研究表明利用现场CTD 数据可以提高声速剖面的反演精度。若是不考虑EOF 基函数和历史平均声速剖面的代表性误差，图6 的结果可以认为是EOF 系数准确时，声速剖面反演精度的最高值，因此本文将之作为衡量反演方法优劣的标准。Casagrande 等[23]曾在研究中给出了EOF系数的物理解释，第1 阶EOF 系数 α1表示了温跃层的垂直位移，即 α1越大则代表温跃层越浅，跃层深度的变化周期也反映在 α1的演化趋势中，第2 阶EOF 系数α2则表示了温度梯度的改变，在温跃层变化剧烈的时刻，α2取值也比较大。从物理意义来看，第3 阶及以上的EOF 对声速剖面的调制效果不显著。

3.2 海表面遥感数据与声速剖面的相关性分析

如图7a 为平均声速剖面的声速梯度，可以发现60～130 m 的跃层部分梯度较大，130～400 m 的跃层部分梯度较小，梯度极大值约在106 m。图7b 为SST、SLA 和声速剖面（Sound Speed Profile，SSP）在0～1 975 m 深度的相关图，从图中可以发现，SST 与SSP 的相关性在上层随着深度增加不断减小，说明SST 可以约束剖面的表层精度；SLA 在60～130 m 深度内，具有中度相关性，SLA 与SSP 的相关性最大值约在103 m，与平均声速剖面声速梯度的极大值深度106 m 相近。在130～400 m 跃层深度内，声速梯度在0.1 s−1附近，该梯度相比于60～130 m 深度梯度较小，但比其他深度的梯度要大，而该范围的声速与SST、SLA 的相关性很弱，这也是误差集中在130～>400 m深度的主要原因。由以上分析可知，由于海面遥感数据可以反映表层声速剖面的结构变化，又由于深层海水的声速比较稳定，因此这两部分反演结果的误差较小。但是对于梯度较小的跃层部分（130～400 m），其声速相对深海来讲扰动较强烈，然而该深度处的声速与SST、SLA 的相关性极弱，从而导致该深度范围的声速反演误差较大。

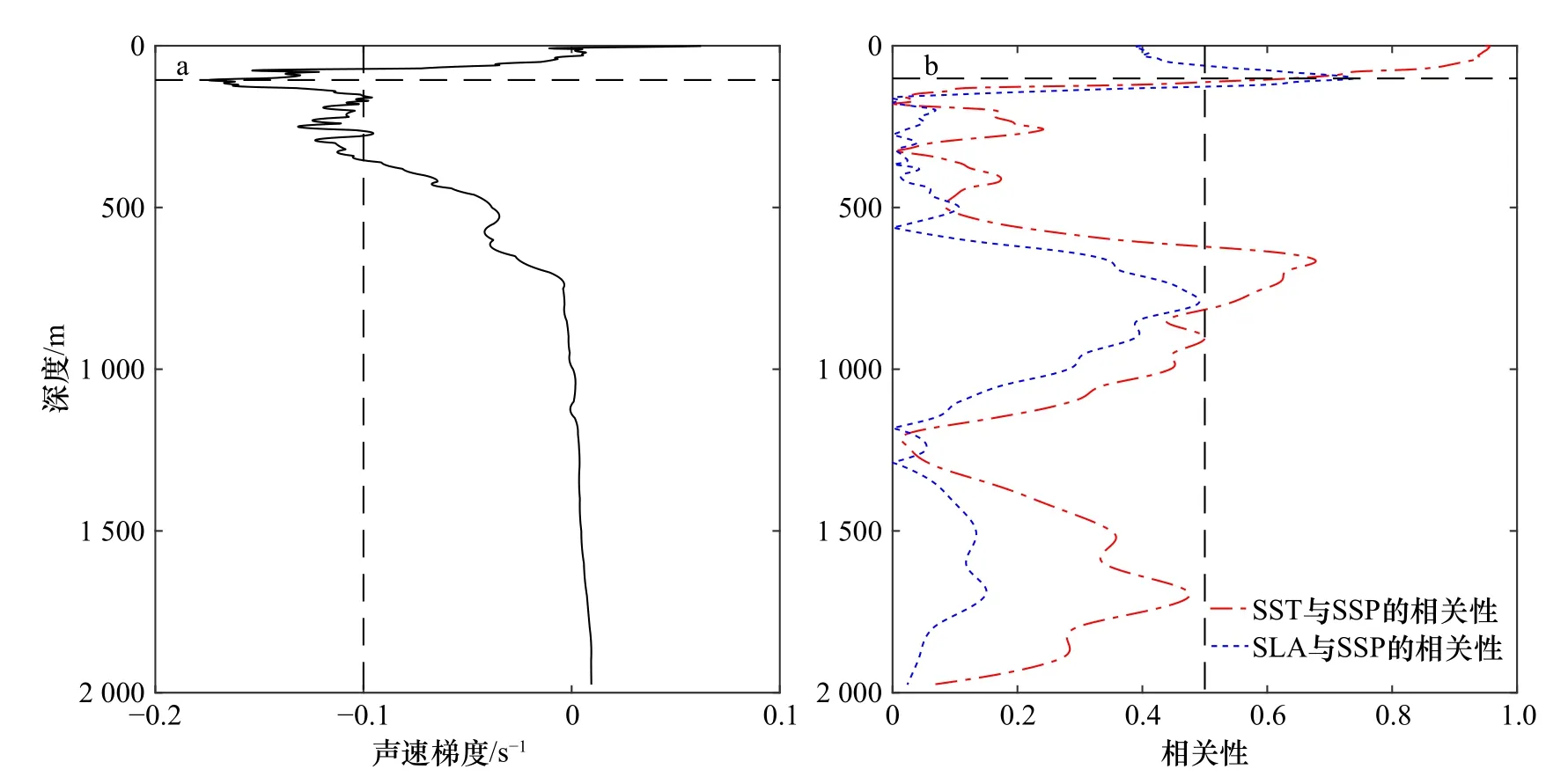
图7 平均声速剖面的声速梯度（a），海表面温度（SST）、海表面高度异常（SLA）和声速剖面（SSP）的相关性（b）Fig.7 Sound speed gradient of mean sound speed profile (a),correlation between sea surface temperature (SST),sea level anomally(SLA) and sound speed profile (SSP) (b)

3.3 声速剖面反演及结果分析

SOM 神经网络是将训练集的SST、SLA、经度（LON）、纬度（LAT）、表层声速仪测量数据和前5 阶EOF 系数利用自组织网络算法映射到输出层不同单元上，每个单元代表一类聚类分析的参考向量。由于缺少表层声速仪实测数据，本文将Argo 剖面在10 m深度处的声速c10假设为表层声速仪的测量值，若具备表层声速仪的实测数据，那么该固定深度替换为表层声速仪的实际测量深度。反演声速剖面的过程是在输出层单元上寻找与待反演剖面已知信息的最小欧氏距离对应的单元，已知信息包括位置信息（LON，LAT），对应位置的海面遥感数据（SST，SLA）以及10 m深度处声速c10，最佳匹配单元中的参考向量即为反演的EOF 系数PCk，结合利用训练集得到的EOF 基函数和平均声速剖面得到声速剖面的估计值。

竞争层节点数由经验公式（13）确定，经过调试发现使用48 个类，初始邻域半径和最终邻域半径分别为4 和0.1 时，均方根误差最小，声速剖面估计效果最好。

确定竞争层最少节点数的经验公式如下：

式中，N代表训练样本的个数。

经典sEOF-r 方法的计算过程大致为：由声速剖面的重构方程（6）计算出训练集中每条剖面对应的EOF 系数。将EOF 系数PC与海面数据建立一阶线性回归关系，利用训练集中的SLA、SST 数据，得到拟合系数的最小二乘估计。进而利用测试集中的SST 和SLA 数据可以计算得到声速剖面的估计值。

EOF 系数与海面遥感数据建立线性回归关系的表达式为

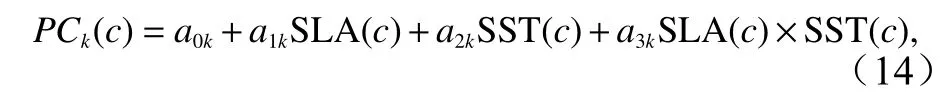
式中，k为选取的EOF 阶数；ak为拟合系数。利用训练集中的SLA、SST 数据，得到拟合系数的最小二乘估计。进而利用测试集中的SST 和SLA 数据可以计算得到声速剖面的估计值。

为了表述方便，这里将本文提出的方法表示为SOM-c10方法。图8 给出不同方法反演得到的声速剖面绝对误差，其中图8a 为 SOM-c10方法的反演结果，与实际测试集声速剖面在0～1 975 m 海深所有剖面的绝对误差约不超过5.02 m/s。图8b 为未考虑表层声速仪数据的经典SOM 神经网络，利用SST、SLA、经度（LON）、纬度（LAT）以及前5 阶EOF 系数训练模型的反演结果，可以发现17 号剖面在350 m 附近的反演误差最大，约为6.20 m/s。图8c 为sEOF-r 方法的反演结果，可以发现第20 号剖面在220 m 附近的反演误差最大，约为7.22 m/s。与经典SOM 神经网络相比，SOM-c10方法的最大误差降低约1 m/s，并且15～18 号剖面反演结果明显变好；与经典sEOF-r 方法相比 S OM-c10方法的最大误差降低约2 m/s。

图8 测试集中声速剖面反演误差Fig.8 The inversion error of the sound speed profiles in the test set

根据均方根误差公式（12），图9 给出不同方法的均方根误差随测试集声速剖面的变化，其中最小二乘解与图6 中的一致。可以看出，SOM-c10方法的最大均方根误差约为1.36 m/s，最小均方根误差约为0.57 m/s，标准差为0.16 m/s；经典SOM 神经网络的最大均方根误差约为1.69 m/s，最小均方根误差约为0.59 m/s，标准差为0.24 m/s；sEOF-r 方法的最大均方根误差约为1.86 m/s，最小均方根误差约为0.67 m/s，标准差为0.35 m/s。图9 表明，本文提出的 SOM-c10方法性能最稳定，除第13～18 号剖面以外，其他情况下的反演精度最高。相反，sEOF-r 方法的性能最不稳定，其对第13～18 号剖面的反演精度最高，然而对其他剖面的反演精度却是很低。

图9 不同方法的均方根误差Fig.9 The root mean square error for different methods

图10 绘制出了测试集中的第13～18 号声速剖面，可见这6 条剖面大致可以分为两类，第Ⅰ类为黑色实线表示的剖面（第13，14 号声速剖面），有两个较明显的负跃层；第Ⅱ类为红色实线表示的剖面（15～18 号声速剖面），在100～300 m 水深处，其声速梯度变化较小，而在320 m 附近出现正梯度。

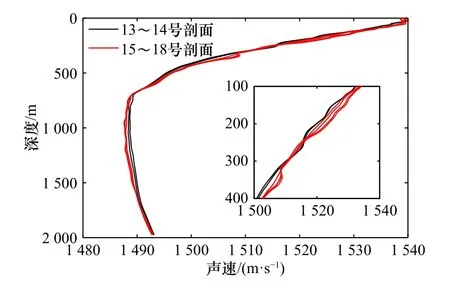
图10 测试集中的13～18 号声速剖面Fig.10 The 13th−18th sound speed profiles in the test set

以第13 号和16 号剖面为例，图11 给出了sEOF-r方法和 SOM-c10方法的反演结果，从图中不难看出，sEOF-r 方法的反演结果与实测值更加吻合，而SOM-c10方法在跃层处的误差显著。相比于sEOF-r 方法，SOM神经网络不仅利用海面遥感数据，还考虑了剖面的位置信息。然而更多的先验信息却带来较高的反演误差，其原因有可能是训练集的水平位置分辨率不高。因为研究表明，SOM 神经网络在反演该6 条剖面的EOF 系数时，匹配到训练结果的同一个神经元，即相同的EOF 系数。从图9 不同方法的均方根误差结果可以发现，SOM-c10方法反演的13 号、14 号剖面比15～18 号剖面的均方根误差要小，说明反演的EOF 系数得到的声速剖面与测试集的13 号、14 号这类剖面更接近。

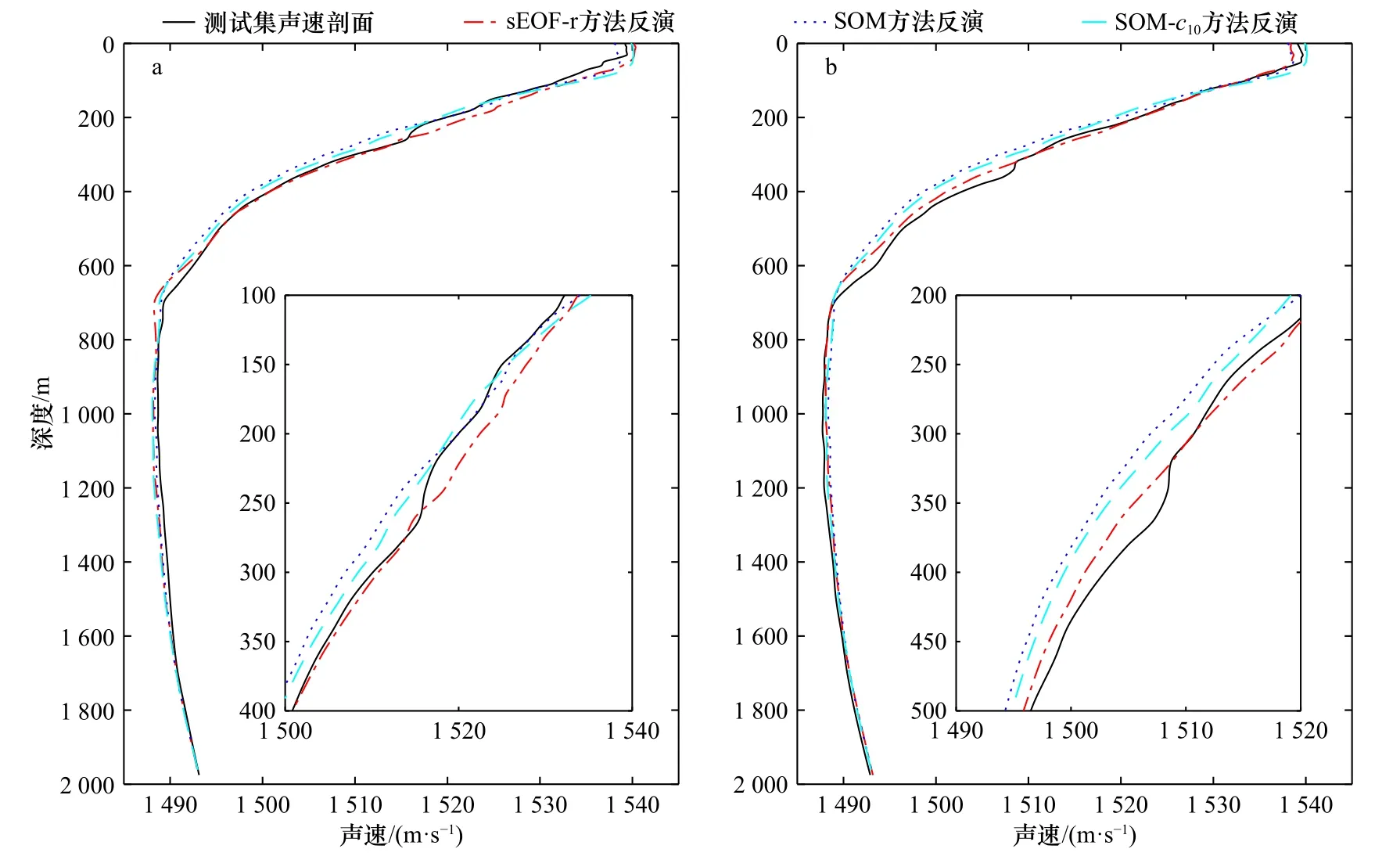
图11 测试集中第13 号剖面（a）和第16 号剖面（b）的反演情况Fig.11 The inversion of 13th profile (a) and 16th profile (b) in the test set

对于减小平均声速剖面的代表性误差，是比较容易实现的，通常在海上作业时会利用CTD 通过定点测量方式获取几个站位的海水声速剖面来消除声速误差的影响，该实时测量的声速剖面一般会比历史平均声速剖面更具有代表性，在一定程度上可以提高反演精度。因此本文从测试集中选取具有代表性的第13 号和17 号剖面，取其平均值作为现场平均声速剖面。图12a 是sEOF-r 方法的反演结果，可见选取新的平均声速剖面之后，大部分均方根误差都略有降低；图12b 是 SOM-c10方法的反演结果，选取新的平均声速剖面之后，大部分均方根误差都有明显降低，且部分均方根误差与最小二乘法结果相近。

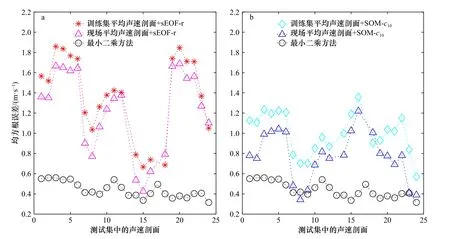
图12 不同平均声速剖面下sEOF-r 和SOM-c10 方法的反演结果Fig.12 Prediction results of sEOF-r and SOM-c10 method with different mean sound speed profiles

4 结论

本文提出一种联合表层声速的自组织映射的非线性反演方法，海表面遥感数据和表层声速仪测量的固定深度处数据（本文选取10 m 深度声速值作为表层声速）作为输入，寻找最佳匹配单元以获得声速剖面的EOF 系数，再结合历史平均声速剖面和基函数来实时反演全海深声速剖面。就印度洋中部海域的实验结果来看，综合考虑表层声速仪的数据后，本文提出的方法反演性能最稳定且精度最高。选择前5 阶EOF 系数可以满足反演方法的精度相关要求，重构的均方根误差在0.5 m/s 附近，该方法也初步解释了海表面遥感数据与声速剖面扰动之间存在关系，同时，在表层和跃层梯度较大的深度范围内，声速剖面与海表面遥感数据具有较高的相关性。

在反演全海深声速剖面时有两点需要引起注意，一是，本文方法对测试集中6 个剖面的反演精度略差于经典sEOF-r 方法，其原因有可能是训练集的水平位置分辨率不高所造成的，SOM 神经网络在处理该6 条剖面时，获得的为同一个最佳匹配单元，即EOF系数相同。二是，声速剖面基函数的代表性问题。这也是作者下一步拟进行研究的问题。