联合重力异常和重力垂直梯度异常数据反演皇帝山海域海底地形

2022-02-04阳凡林沈瑞杰梅赛屠泽杰辛明真

海洋学报 2022年12期

阳凡林，沈瑞杰，梅赛，屠泽杰，辛明真

(1.山东科技大学测绘与空间信息学院，山东青岛 266590；2.自然资源部海洋测绘重点实验室，山东青岛 266590；3.中国地质调查局青岛海洋地质研究所，山东青岛 266237)

1 引言

海洋约占地球表面积的71%，蕴藏着极其丰富的矿产和生物资源。海底地形数据是研究海洋生物、海洋化学及海洋地球物理学等相关学科的基础。自20 世纪50 年代回波测深技术广泛应用以来，搭载单波束和多波束的研究船可以开展高精度、高分辨率的海底地形勘测。然而船载水深测量存在效率低、测量结果分布不均匀的问题，使用回声测深技术对全球海底地形进行完全覆盖式勘测仍需要很长时间[1]。

卫星测高技术的出现，可以全天候、连续准确地在全球范围内直接获取海面高度的观测数据，其测量效率和覆盖范围是船载水深测量无法比拟的。随着卫星测高资料的积累，利用测高数据获取的海洋重力信息已成为反演海底地形的主要数据来源。目前，利用重力数据进行海底地形反演的研究方法主要有：重力地质法（Gravity Geologic Method，GGM）[2–3]、导纳函数法（Admittance Method）[4]、最小二乘配置法（Least Squares Collocation，LSC）[5–6]和Smith and Sandwell（SAS）法[7]。其中，GGM 和SAS 法使用最为广泛，两者大多以重力异常数据作为输入。Kim 等[8]将GGM 与SAS法构建的海底地形模型进行比较，发现GGM 在预测短波长（≤12 km）分量方面具有优势，而SAS 方法在预测长波长（≥25 km）分量方面具有优势；李倩倩和鲍李峰[9]，彭聪等[10]均对SAS 方法和GGM 进行了比较分析，后者给出了两种方法的水深和海底地形复杂程度的适用条件；范雕等[11]应用导纳函数法建立了不同均衡补偿模式下的海底地形模型，并对各项地球物理参数的影响进行了详细分析；郭金运等[12]利用迭代延拓法，提升了重力异常向下延拓的精度。

除重力异常外，重力垂直梯度异常（Vertical Gravity Gradient Anomalies，VGG）也是反演海底地形的重要数据，其反映了重力场在垂直方向上的变化情况，且重力垂直梯度异常相比于重力异常含有更多的高频信号成分，能够更好地描述异常特征[13–14]；Wang[15]指出大洋地壳的质量补偿对重力梯度的影响很小，提出可以利用重力垂直梯度异常反演水深的思路；Wessel 和Lyons[16]通过对高斯型海山模型的研究，指出重力垂直梯度异常具有放大短波信号、抑制长波信号的作用；吴云孙等[17]推导了重力垂直梯度异常与海底地形之间的关系并反演了南海海域的海底地形模型；胡敏章等[18]通过叠加重力异常（波长<100 km）和重力垂直梯度异常（波长100～200 km）反演的海底地形构建了中国海域的海底地形模型，其精度与V15.1 相近；范雕等[19]利用多元回归分析技术，通过解算重力异常和重力垂直梯度异常的偏回归系数和常数项来反演海底地形。

目前，联合重力异常和重力垂直梯度异常数据进行海底地形反演的研究较少。本文针对重力异常、重力垂直梯度异常和船测水深数据各自的特性，通过稳健回归分析降低了船测数据和重力数据中异常点的偏差影响，分别使用重力异常和重力垂直梯度异常数据反演了太平洋皇帝山海域（35°～45°N，165°～175°E）的海底地形模型，采用滑动窗口赋权的方法，选择滑动窗口内的最优权值，联合两种重力数据构建的模型。最后，以船测水深数据为外部检核，与DTU18 和SIO V23.1 全球海底地形模型以及地形剖面处的实测水深数据进行比较分析。

2 研究区域和数据来源

夏威夷皇帝海山链位于太平洋西北侧，该区域存在海底山脉且两侧海隆聚集，海底深度跨度大（200～8 000 m），是开展海底地形反演的热点区域。本文选取的研究区域位于其南部（35°～45°N，165°～175°E），考虑到边缘效应，将研究区域的经纬度均向外扩充1°，研究区域如图1 所示。

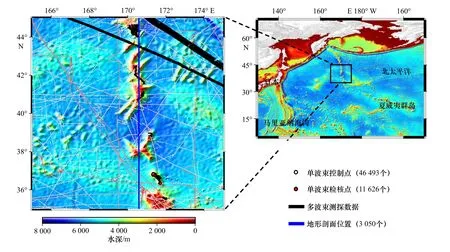
图1 研究区域与船载测深轨迹分布Fig.1 Study area and shipborne bathymetry trace distribution map

2.1 船载测深数据

本文采用的船载测深数据来自于美国国家地球物理数据中心（National Geophysical Data Center，NGDC）发布的实测数据，其中单波束数据时间跨度为42 a（1961–2002 年），多波束数据时间跨度为16 a（2004–2019 年）。由于早期数据可能存在测量误差，以全球地形模型ETOPO1 作为约束条件进行互差比较，依照“3σ”准则，采用10′×10′的窗口大小，5′的移动步长滑动剔除单波束数据中的粗差点，得到61 169 个单波束船测点。均匀选取其中4/5 的船测点作为控制点，剩余船测单波束数据和滤波抽稀后的多波束数据用于后续模型的精度评定及地形剖面对比。

2.2 重力数据

重力异常数据（图2a）和重力垂直梯度异常数据（图2b）均来源于加州大学圣地亚哥分校（University of California,San Diego，UCSD）的斯克里普斯海洋研究所（Scripps Institution of Oceanography，SIO）于2021年8 月发布的V31.1 版本，格网分辨率为1′×1′。对比先前版本，V31.1 模型补充了新的Altika、Cryosat LRM、Cryosat SAR 和Sentinel-3A/B 卫星测高数据。为了方便说明，下文将重力异常和重力垂直梯度异常数据合称为重力数据。

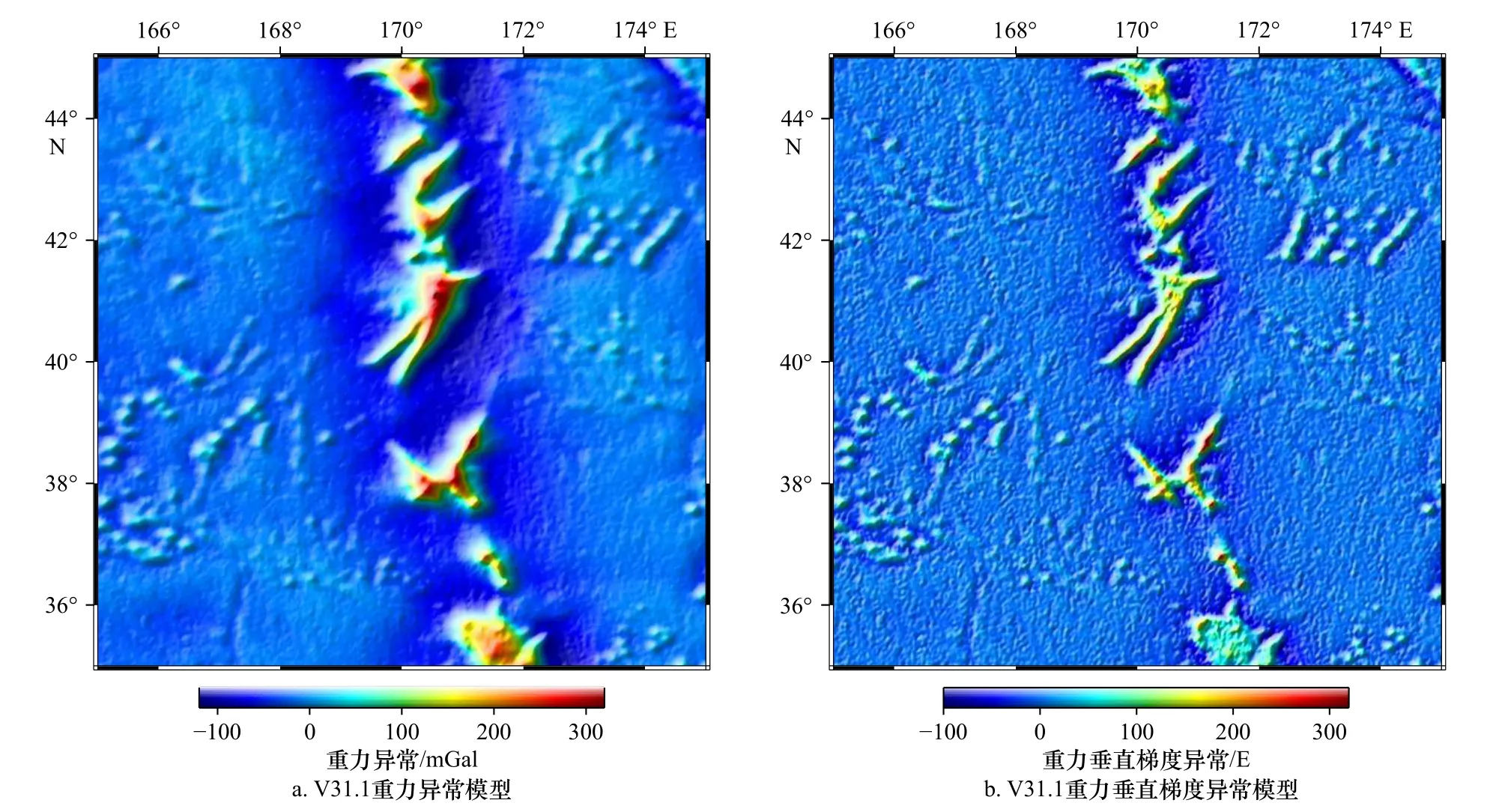
图2 重力模型示意图Fig.2 Gravimetric model diagram

2.3 海底地形模型

本文采用目前广泛使用的ETOPO1、DTU18 和SIO V23.1 海底地形模型（1′×1′）作为参考模型。

ETOPO1 由美国国家地球物理中心（National Geophysical Data Center，NGDC）和美国国家海洋和大气管理局（National Oceanic and Atmospheric Administration，NOAA）于2008 年8 月发布，该模型集成了来自区域和全球数据集的地形、测深和海岸线数据。

DTU18 由丹麦科技大学（Technical University of Denmark，DTU）于2019 年9 月发布，该模型补充使用了3 a 的Sentinel-3A 卫星和7 a 的Cryosat-2 LRM 卫星数据，并使用FES2014 海潮模型进行潮汐改正。

SIO V23.1 由美国SIO 的Sandwell 团队于2021 年11 月发布，该模型结合了最新的重力模型数据、卫星测高数据以及优化的船测水深数据，是公认精度最高的全球海底地形模型之一。

3 海底地形反演方法

Smith 和Sandwell[7]于1994 年提出了依据线性回归分析技术反演海底地形的方法。其基本原理是利用重力数据和海底地形在强相关性波段内的线性关系，反演一定波段的海底地形，并叠加其他波段的船测水深数据得到全波段海底地形模型。由于线性回归分析技术会受到重力数据或船测数据中一定异常点的影响，因此采用稳健回归分析法，提高线性回归分析中比例因子的鲁棒性；并提出滑动窗口赋权，联合由重力异常和重力垂直梯度异常构建的模型，通过对窗口内的两种模型分配最优权值，构建研究海域最终的海底地形模型。下面对使用的方法进行具体介绍。

3.1 反演波段的选择

Parker[20]于1973 年将快速傅里叶变换[21]应用到位理论，根据Parker 公式，在不顾及地壳挠曲均衡影响下，海底地形与重力异常G0(k)之间的关系可以描述为

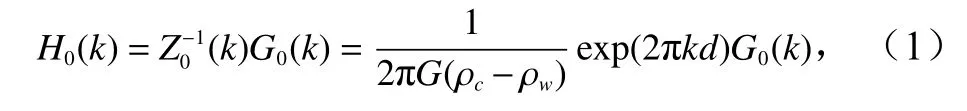
同理，海底地形与重力垂直梯度异常G1(k)之间的关系可以描述为[18]

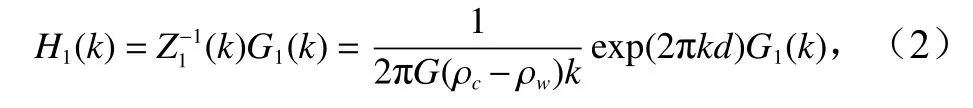
式中，G为地球引力常数；k为径向频率(kx,ky)=(1/λx,1/λy) ），其中 (kx,ky)和(λx,λy)分别为x和y方向的频率和波长；d为平均海深值；ρc和ρw分别为地壳和海水密度；Z(k)为导纳函数。

由Parker 公式可知，在频率域内重力数据和海底地形在一定波段范围内具有相干性，若将重力数据和水深看作两种不同的信号，两者的相干性可以表示为

式中，r2(k)为互谱相干函数，当r2(k)趋近于1 时，说明两种信号呈线性相关，趋近于0 时，说明两种信号完全不相干；G(k)、H(k)分别代表重力信号和地形信号的傅里叶变换；G*(k)、H*(k)表示为G(k)、H(k)的复数共轭。研究海域内重力数据与海底地形相干性关系如图3 所示。

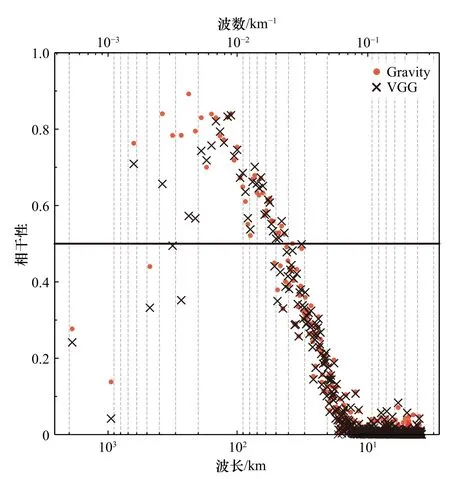
图3 重力数据与海底地形的相干性Fig.3 Coherence between gravimetric data and seafloor topography

重力垂直梯度异常在50～200 km 波长范围内与海底地形相干性大于0.5，而重力异常数据在50～400 km 波长范围内相干性大于0.5，考虑到在波长大于200 km 时，会受到地壳均衡补偿影响[22]，海底地形产生很少或没有重力场变化，因此本文选择的反演波段为50～200 km。

3.2 稳健回归分析

稳健回归分析的原理是基于最小二乘估计的迭代加权法，通过对权的优选以提高拟合精度与可靠性，使参数的估值尽可能避免粗差的影响，得到正常模式下的最佳估值[23]，对于线性回归模型

Huber 函数将残差分为两组：一组残差超过初始标准差的某个因子c，另一组残差不超过这个限制。u代表标准化的残差指标（ui=vi/σ0），σ0为单位权中误差，c表示调和系数，本文取c=2。参数a的稳健估计可用迭代加权最小二乘求解，陈艳国[25]指出了具体求解步骤。反演波段的重力数据和船测水深数据线性拟合结果如图4 所示。

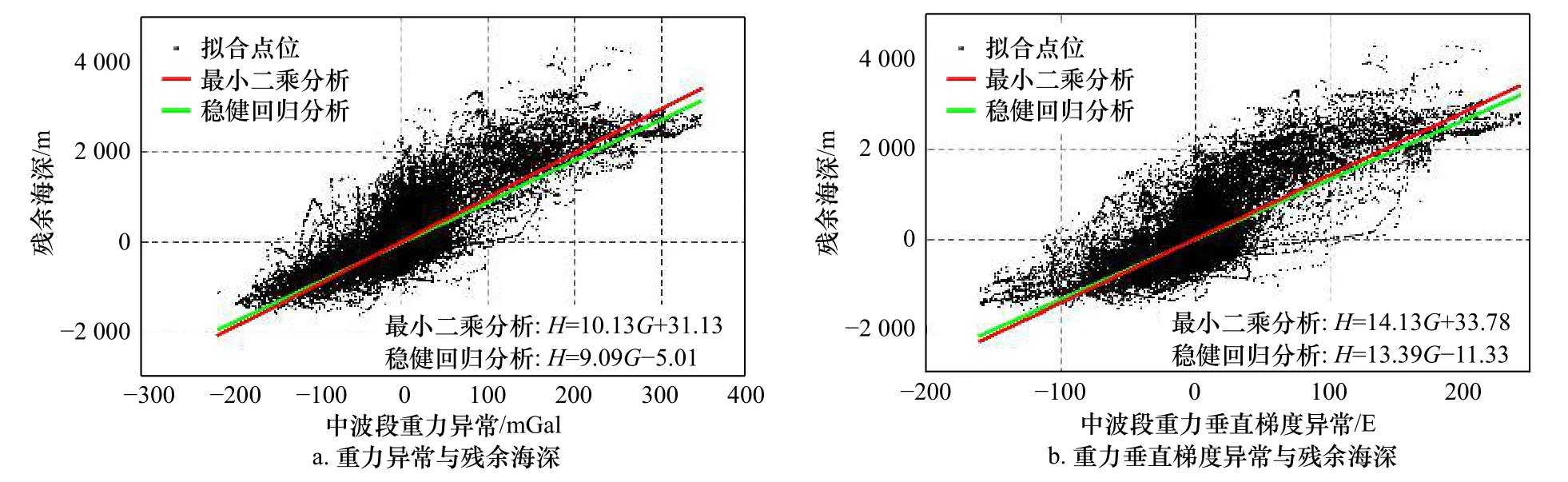
图4 反演波段重力数据与残余海深线性拟合结果Fig.4 Results of linear fitting between gravity data of inversion band and residual sea depth

可以看出，在研究海域，重力数据与残余海深在反演波段表现出了良好的线性关系。文献[26]指出，传统的最小二乘分析相比于稳健回归分析更容易受到离群点的影响，导致其斜率（即比例因子）倾向于离群点，而利用Huber 损失函数的稳健回归分析通过给予离群点较小的权值，能够减小对离群点的敏感度问题，以此提高比例因子的鲁棒性。

3.3 滑动窗口赋权

滑动窗口赋权是建立在最小二乘赋权[27]的基础上，将重力异常反演的模型G0(i)和重力垂直梯度异常反演的模型G1(i)与船测水深值H(i)进行计算。假设滑动窗口内G0(i)所占的权重为xi，则G1(i)所占的权重为1−xi，融合得到的G′(i)可表示为

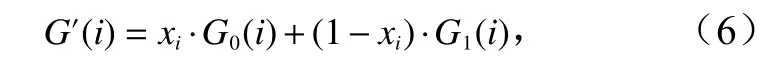
将融合后的G′(i)和H(i)进行比较，以其差值的标准差最小为准则分配最优权值，计算公式为

以此对滑动窗口内的G0(i)和G1(i)分配最优权值，进而融合得到区域不同地形起伏条件下的权值分配。研究海域内，重力垂直梯度异常模型的权值分配如图5 所示。

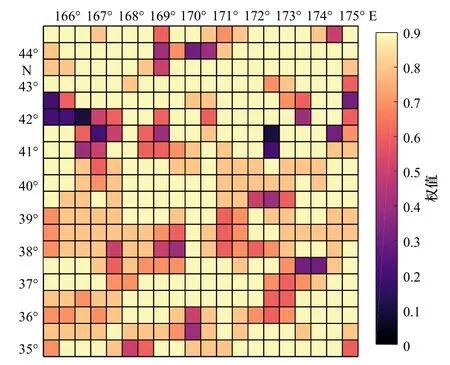
图5 重力垂直梯度异常模型权值xi 分配示意图，相应的，重力异常模型的权值分配为1−xiFig.5 The schematic diagram of weight distribution xi of vertical gravity gradient anomalies model.Accordingly,the weight distribution of gravity anomalies model is 1−xi

基于上述分析，本文反演海底地形模型的基本流程如图6 所示。

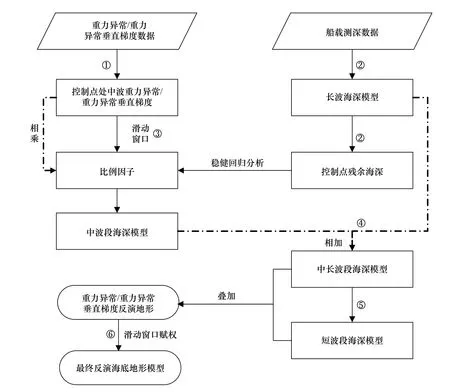
图6 海底地形反演流程Fig.6 Flowchart of seafloor topography inversion

①通过相干性分析，获取重力数据和海底地形之间相干性高的波段作为反演波段，将重力数据进行带通滤波和向下延拓处理，获得反演波段的重力数据G(x)并插值到船测控制点处；

② 将格网化的船载测深数据进行低通滤波得到长波海深模型，内插至船测控制点处与海深值做差得到控制点处残余海深；

③将步骤①的中波重力数据与步骤②的残余海深以滑动窗口方式进行稳健回归分析，解算格网点处比例因子S(x)和常数项；

④ 将比例因子S(x)和重力数据G(x)相乘并叠加常数项得到反演波段海底地形，与长波海深模型相加得到中长波海深模型；

⑤ 将中长波海深模型内插至船测控制点得到控制点处中长波水深值，与控制点处水深测量值做差得到控制点处短波水深并格网化，最后与中长波海底地形模型相加得到全波段海底地形模型；

⑥ 采用滑动窗口赋权融合重力异常和重力垂直梯度异常数据构建的海底地形模型，得到最终的海底地形模型。

4 模型构建结果及精度评价

4.1 多源海底地形模型的构建

以20′×20′的窗口大小[28]，通过稳健回归分析拟合格网处比例因子和常数项。分别将重力异常和重力垂直梯度异常构建的模型称为SGA（Single Gravity Anomalies）和SVG（Single Vertical Gradient）。以SGA和SVG 模型与船测检核点间标准差最小为准则，采用滑动窗口赋权法以30′×30′的窗口大小，将SGA 和SVG 模型分配窗口内的最优权值，融合构建的最终模型称为MGM（Multiple Gravity Model），反演结果如图7 所示。

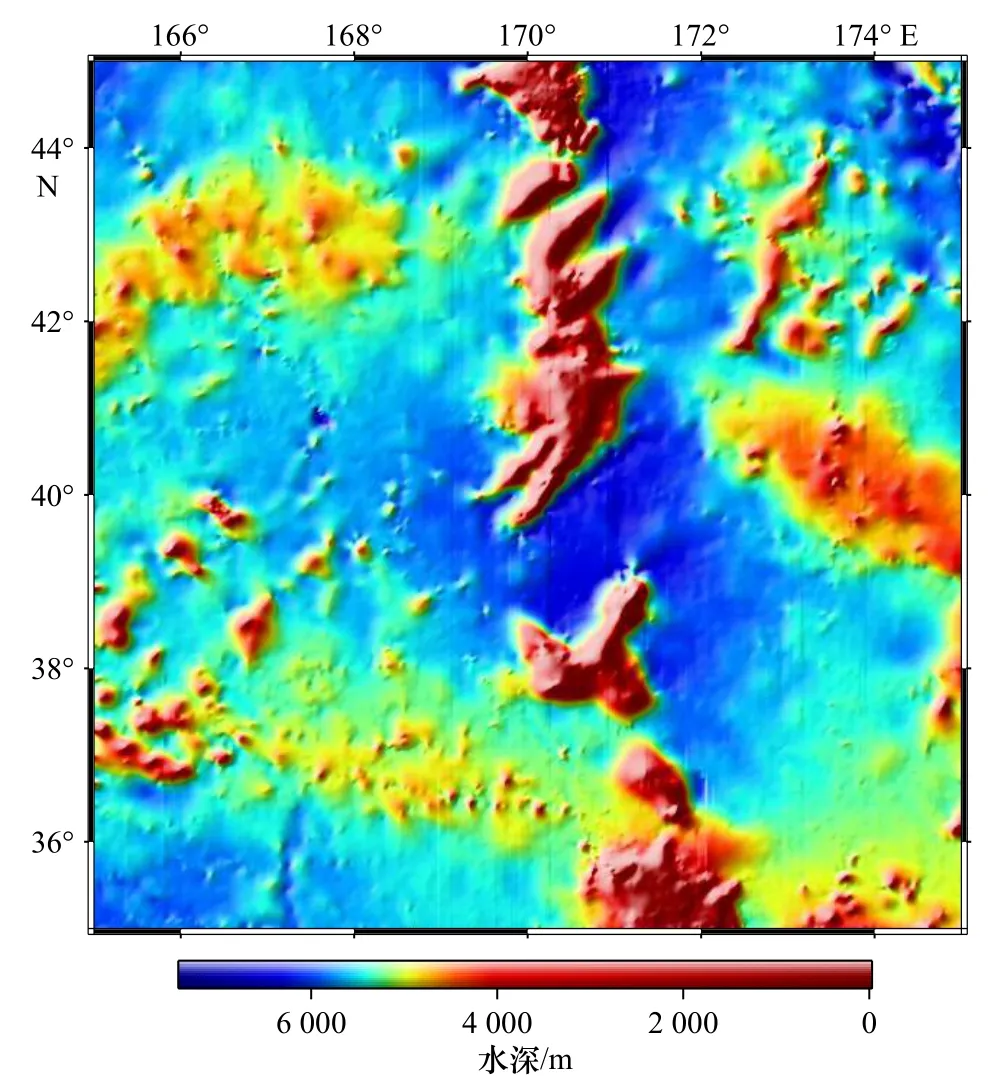
图7 MGM 海底地形模型Fig.7 The seafloor topography model of multiple gravity model

4.2 与单一重力数据源模型比较分析

为验证本文方法的优越性，对SGA、SVG、传统最小二乘赋权法（MGM_LS）和MGM 4 种模型进行比较分析，考虑到构建以上4 种模型时均未使用多波束数据进行约束，且多波束数据集中分布在地形起伏变化剧烈海域，因此使用该数据作为外部检核条件，得到的统计结果如表1 所示。

表1 海底地形模型与多波束数据差值统计结果Table 1 Difference statistics of seafloor topographic model with multibeam data

以标准差作为质量评估依据，SVG 模型相较于SGA 模型，其精度提高了13.11%，表明在地形起伏变化剧烈的区域，重力垂直梯度异常能更好的反映地形起伏变化；使用传统最小二乘赋权法构建的模型MGM_LS，其精度低于SVG 模型，而通过滑动窗口赋权构建的模型MGM 相较于仅使用单一重力数据构建的SGA 和SVG 模型，精度分别提高了14.92%和2.08%左右，表明本文采用的滑动窗口赋权融合了两种重力数据在不同地形起伏变化下的反演优势，在复杂海域的水深反演表现更为突出。

4.3 MGM 精度评价

船测水深数据在预处理后，可作为研究海域内的真值对反演模型进行外部检核。将MGM 内插至船测水深处与船测水深值做差，并定义模型与检核点海深差值与检核点海深值之比作为相对误差，得到的差值分布如图8 所示。

结合图8a 和图8b，MGM 与单波束测深数据在绝大部分海域差值较小，与多波束测深数据差值较大的区域分布在地形起伏变化剧烈的海山链、海隆与海沟交界处；根据直方图统计，差值大于1 000 m 的仅占4.48%，可能是由于多波束实测数据集中分布在地形变化幅度大的海域，存在粗差未剔除；由图8c 可知，在两侧相对平坦海域，MGM 相对误差保持在3%以下，精度较高；在中心海山链区域，相对误差在10%～50%范围内占比约为7%，是模型的主要误差源。

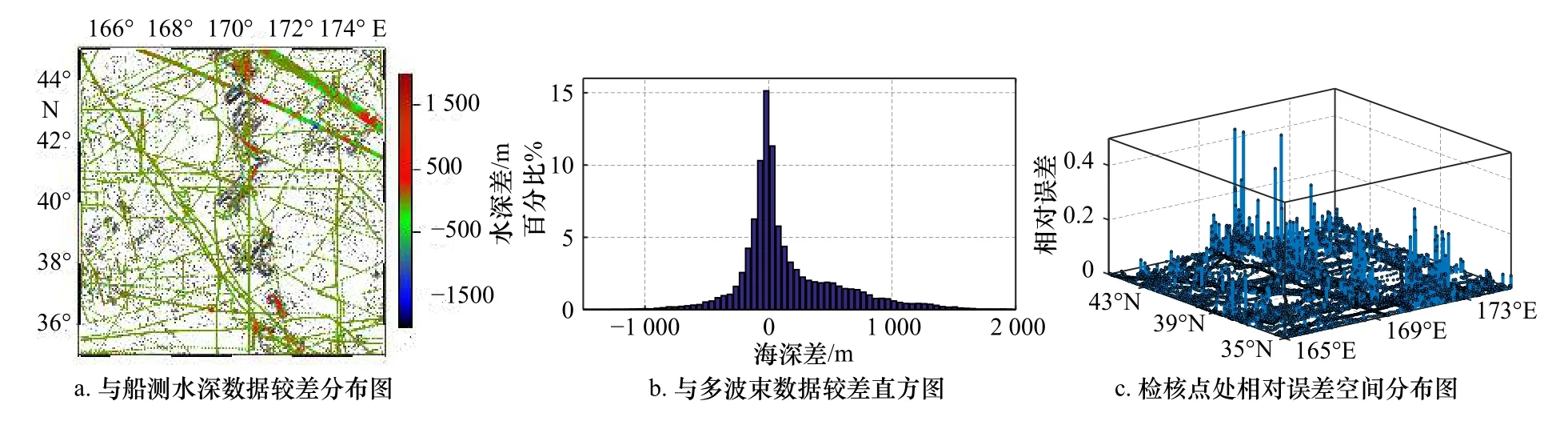
图8 MGM 差值分布图Fig.8 Difference distribution diagram of multiple gravity model

为进一步验证MGM 的可靠性，引入DTU18 和V23.1 模型进行比较分析，得到的统计结果如表2所示。

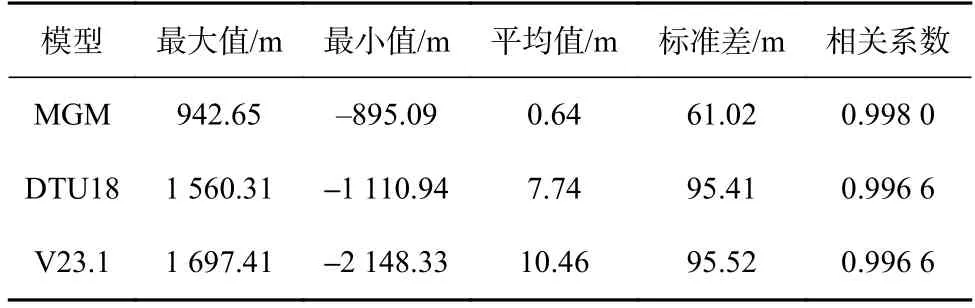
表2 海底地形模型在检核点处差值统计结果Table 2 Difference statistics of seafloor topographic model at check point

由表2 知，在研究海域，本文联合重力异常和重力垂直梯度异常构建的模型MGM，其误差极值更小，相较于DTU18 和V23.1 模型，其精度提高了约36%。其次，MGM 与船测数据间相关系数达0.998 0，表明MGM 与实测水深数据更为贴近。由于3 种模型中均存在与船测水深数据差值较大的点，但仅占检核点总数的极小部分，为直观看出其分布情况，取相对误差大于6%的点位作为精度较低的异常点。分别统计模型与检核点差值在400 m 内的频率分布直方图（图9）以及精度较低的异常点位分布图（图10）。

图9 检核点处差值结果统计直方图Fig.9 Statistical histogram of the difference results at the check point

图10 异常点空间位置分布图（黑色圆点代表异常点位）Fig.10 Spatial distribution map of outliers (black dots represent outliers)

根据直方图可看出，MGM 与船测水深数据一致性良好，两者差值在300 m 以内的占比达99.42%，优于DTU18 和V23.1 模型的98.12%和98.66%，相较于以上两种模型，MGM 的异常点数量分别减少了21.18%和17.32%，表明在地形起伏变化剧烈海域，MGM 仍与船测水深数据间有较好的拟合效果。基于前文分析，3 种模型在异常点位的空间位置分布上具有一致性，主要集中在中心海山链附近，该部分海域地形起伏变化剧烈，对反演地形容易造成较大的影响。

地形剖面图可以直观反映出剖面线上的地形起伏情况。为进一步探究皇帝海山链区域对反演精度的影响，提取其地形剖面进行比较分析[29]，结果如图11所示。其中蓝色曲线代表MGM 绘制的地形剖面图，红色曲线代表船测水深数据，可作为该地形剖面的实际地形。

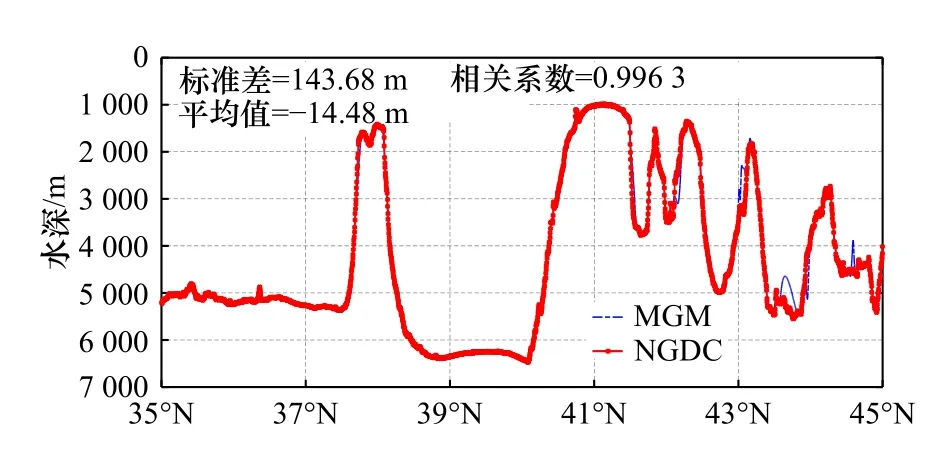
图11 皇帝海山链地形剖面图Fig.11 The topographic profile of the Emperor Seamount Chain

由图11 知，皇帝海山链区域的整体地形走势清晰明显，该剖面的海深范围为984～6 475 m，平均水深约为4 428 m。MGM 与实测数据的差异主要分布在42°～44°N 海域附近，该区域地形起伏变化剧烈，海山海沟连续交错，对反演结果造成了一定程度的影响。整体上，MGM 与实测水深数据在描述海山地形走势上表现出了良好的一致性，两者相关性达0.996 3。

综上所述，文中利用滑动窗口赋权联合重力异常与重力垂直梯度异常反演海底地形的方法具有较强的可行性，尤其在地形起伏变化剧烈的海域，可有效提高海底地形反演精度。