基于FHN 神经元自适应多通道随机共振图像增强*

房 涛，方琳灵，刘 艳，潘树文

(1.浙大城市学院信息与电气工程学院，浙江 杭州 310005；2.中国移动杭州研发中心融合通信系统部，浙江 杭州 311121)

图像是人们获取外界信息的主要方式，但现实生活中图像在获取、处理、传输和显示的过程中，都会难以避免地受到各种各样外界噪声的干扰，使得图像的成像质量严重退化，这是非常不利于后续更高层次的图像处理任务的，比如图像分类、目标检测等等[1-2]。因此，如何提高图像的质量，对于后续相关的图像分析研究是非常有意义的。

图像增强的方法是非常丰富多样的，很多的学者依据自己的研究内容也在不断地提出新的图像增强算法[3-4]。首先是基于灰度变换和直方图均衡化等空域的图像增强算法，灰度变换主要通过变换函数改变像素灰度的动态变化范围，以增强图像灰度级细节，一般包括线性变换、分段线性变换、非线性变换等等[5]；直方图均衡化则是通过对图像进行非线性拉伸变换，对原始图像的像素值进行重新分配，使得不同灰度级别范围内的像素数量保持均匀性[6]。在空域的基础上，研究人员进一步借助傅里叶变换等方法将图像变换到频率空间域后通过非线性滤波算法处理，实现图像的增强处理，其主要包含低通滤波、高通滤波以及同态滤波等等[7]。随着仿生视觉的发展，基于视网膜-大脑皮层(Retinex)理论在图像增强方面也得到了快速发展与应用，单尺度Retinex 和多尺度Retinex 图像增强算法陆续被提出，在实际应用过程中也具有比较好的效果[8]；同时在考虑到图像存在局部细节色彩失真的情况，研究人员在多尺度Retinex 算法的基础上又进一步提出了包含色彩恢复因子的Retinex 图像增强算法[9]。另外，由于深度学习在图像处理领域中应用的广泛，对于不同的外部场景，研究人员也提出了很多有针对性的图像增强算法，比如解决低光照强度下图像增强的LLNet[10]和LightenNet 网络[11]，以及基于生成对抗网络(GAN)的低质CT 图像增强等等[12]。

然而，上述的这些方法多是利用先验知识消除导致图像质量退化的噪声，使得被高斯噪声干扰的图像能够被较好地增强。但是在实际操作过程中图像质量退化过程的信息往往是比较匮乏的，这也导致模型参数是难以被准确估计的[13]。此外，传统的方法多是尽可能把噪声作为干扰而加以消除，然后保留图像中的有用信号。这种策略对处理高信噪比图像是有效果的，但对于噪声与有用信号的特征差异很细微的低信噪比图像，最终也是很难取得理想的图像增强结果[14]。在近些年来，当Benzi 等人[15]在研究周期性复发的冰河期问题时，发现在偏心率如此小的周期性下，地球的气候不足以发生这么大的变化，为了合理地解释这种现象，他们提出了双稳态的非线性气候模型，完美地解释了周期性冰河期的原因，并将这种现象称之为随机共振。自此之后，随机共振吸引了大批学者的研究关注，同时为噪声与弱信号的处理提供了一种新的思路。部分学者利用随机共振机制在处理相关图像任务时也取得了很好的实验结果，比如Marks 等[16]研究了阈值系统在图像增强方面的应用，使得含噪声图像能够具有最佳的视觉效果。

因此，本文受随机共振思路的启发，提出一种基于FHN 神经元自适应的多特征并行通道级联随机共振图像增强方法。首先将原始图像分解为朝向、亮度以及亮度对比度等特征信息独立通道；然后构建基于遗传算法的自适应随机共振多特征并行通道对信息流进行并行处理，通过遗传算法来确定每一个通道FHN 神经元随机共振系统的最优参数，以实现特定噪声自适应最优FHN 神经元参数设置；最终对多通道的输出特征增强信息进行融合，再通过一个级联的FHN 神经元模型对融合后的信息流进行深度优化，实现FHN 神经元非线性系统和带噪声输入图像的最佳匹配，达到噪声、图像输入信号以及FHN 神经元三者之间的随机共振，完成对原始输入图像增强的目的。

1 基本原理

图像由于受到采集设备以及外界噪声干扰的原因，会导致图像质量出现不同程度的退化，这种图片质量的下降往往会对后续图像处理任务产生直接的影响，传统的方法也大多采用滤波等方法去除图像中存在的噪声，这具有一定的局限性。受随机共振思路的启发，将输入图像进行降维，利用随机共振系统，将图像中存在的噪声有效利用实现对退化图像的有效增强。因此对于特定的受噪声干扰的原始输入图像信号，如何寻找合适的共振系统参数就成为了非常重要的研究内容。为了避免图像信息特征的单一性，本文将输入图像的朝向、亮度以及亮度对比度等关键特征信息提取出来，建立单独特征通道；然后在每一个特征通道上构建FHN 神经元自适应求解的随机共振方法，建立多特征通道并行信息处理的机制，并通过遗传算法自动快速迭代求解确定每一个通道FHN 神经元随机共振系统的最优参数，以实现不同特征信息通道的最优输出；然后通过对特征独立通道的最优输出特征增强信息进行融合，再通过一个级联FHN 神经元对并行特征通道融合数据做深度优化，实现FHN 神经元非线性系统和带噪声输入图像的最佳匹配，实现输入图像信噪比的增强，方法原理的整体结构图如图1 所示。

图1 多通道自适应FHN 神经元随机共振原理框图

1.1 FHN 神经元模型随机共振机制

在上世纪50 年代Hodgkin 和Huxley[17]基于乌贼巨轴突的大量电生理实验数据建立了著名的Hodgkin-Huxley(H-H)模型，可以很好地用来研究神经元的相关脉冲发放特性，在保留H-H 模型生物特性的基础上FitzHugh 和Nagumo[18]通过一定的简化，提出了二维FHN 神经元模型，具体表达形式如下:

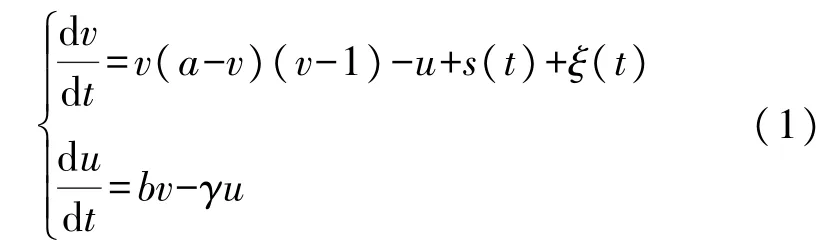
为便于计算，本文考虑高斯白噪声激励下简化的一维FHN 神经元模型，在外加信号刺激的情况下，其Langevin 方程模型如下:

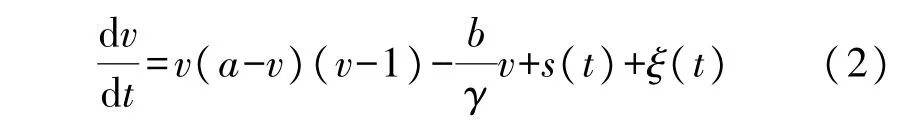
确定性方程的势函数为

式中，v、u分别表示FHN 神经元的膜电压动作电位与离子通道慢过程恢复变量；a反映了膜电压动作电位v的快变程度，b反映了离子通道慢过程恢复变量u对系统的影响，γ为正常数；s(t)为输入信号，ξ(t)为高斯白噪声。令，当系统参数b/γ＜时，势函数有两个稳定点:其中，vsp1表示神经元细胞的膜电位处于静息状态，vsp2则表示神经元细胞的膜电位处于激发态；以及一个不稳定的点vup，具体表达式如下:

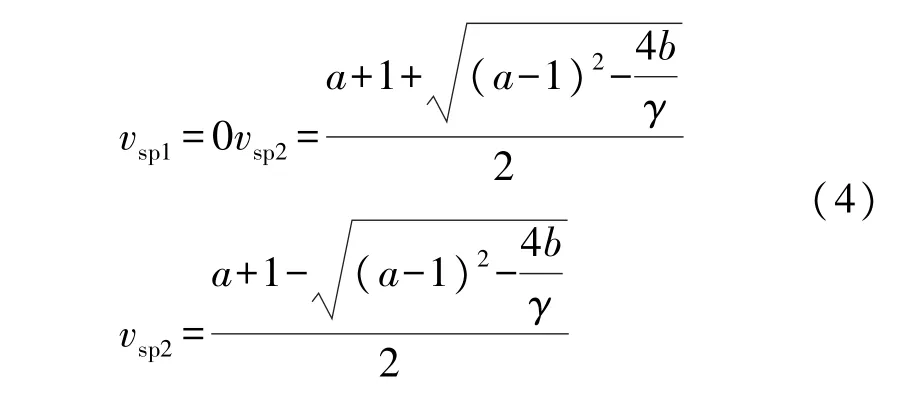
通过消融实验可以发现当FHN 神经元的参数b和γ保持固定不变时，通过改变参数a使其逐渐增大，此时势函数的稳定点会由一个演变为两个再变为一个，二者的势阱深度也会动态变化，一个加深另一个则相应地减弱，不稳定点则会跟着发生相应的改变，其具体变化如图2(a)所示；同理，当FHN神经元的参数a和γ保持固定不变时，通过改变参数b使其逐渐增大，神经元细胞的膜电位处于静息状态时的势阱变化不大，而神经元细胞膜电位处于激发态时的势阱深度则会慢慢减小，直至变得不再稳定，具体如图2(b)所示。

图2 FHN 神经元系统中势函数的示意图

通过上面的分析，在输入信号和噪声一定的情况下，如何确定一维非线性FHN 神经元模型最优的系统参数a和b，使经过随机共振系统输出信号的信噪比相对于输入信号的信噪比之间的信噪比增益可以达到最大值，便成为了一个非常具有价值的研究方向。针对这种情况，本文提出了基于遗传算法的FHN 神经元系统多参数自适应随机共振的弱信号增强方法。

1.2 随机共振信号增强评价指标

图像增强效果的评价方法一般可以分为主观评价和客观评价，而主观评价很容易受到观察者个体不同主观因素的影响，所以本文采用峰值信噪比(Peak Signal to Noise Ratio，PSNR)作为FHN 神经元随机共振效应的评价指标，同时也是本文作为参数优化算法的适应度函数，是一种使用比较广泛且客观的图像质量评价方法[19]，其具体计算方式如式(5)、式(6)所示:

式中，MSE 表示增强后的复原图像与原始图像的均方误差，M和N分别表示增强后的复原图像和原始图像的行数和列数，I(i，j)和K(i，j)分别表示原始图像和增强复原后图像的第i行和j列的像素灰度值，L表示实验图像的灰度等级。

1.3 自适应FHN 神经元随机共振多参数优化

目前针对随机共振系统参数自适应优化主要有蚁群算法、鱼群算法等优化方法[20]，本文采用遗传算法，对各个特征独立通道以及级联中使用的FHN 神经元随机共振系统的参数a、b进行自适应实时同步优化，并将上述介绍的PSNR 评价指标作为适应度函数，构建以多通道并-级联FHN 神经元模型为核心的自适应最优随机共振系统，具体结构如图3 所示。

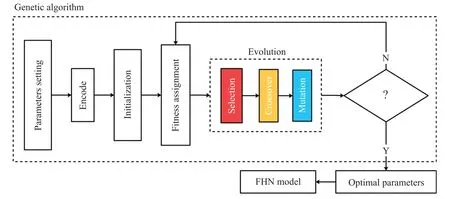
图3 基于遗传算法优化FHN 神经元参数示意图

首先，定义不同特征通道下的FHN 神经元系统参数a、b的搜索空间和精度，设aε[amin，amax]，bε[bmin，bmax]，搜索精度δa＝0.1，δb＝0.01。并根据系统参数的搜索空间和搜索精度，将系统参数a、b二进制编码长度分别设为u_la、u_lb，本实验根据FHN 神经元参数变化特性，可以令u_la＝4、u_lb＝4，即:

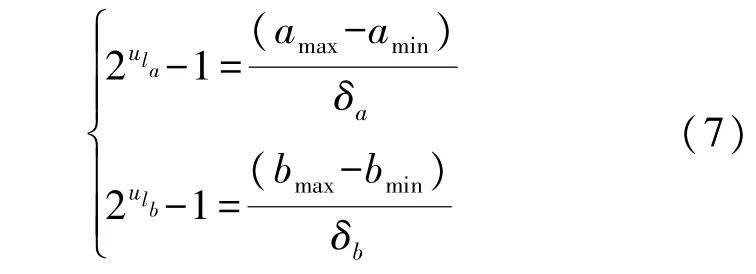
对系统参数a、b进行整体编码，获取相对应的编码字节

其次，进行种群初始化，本实验设定总的种群规模为20，然后根据随机性选取部分个体构成一个初始种群。同时对不同特征通道根据一维FHN 神经元随机共振系统输出信息，计算增强评价指标PSNR 作为适应度函数，即PSNR ＝f(a，b)，根据式(5)和(6)，进行适应度计算，并求解出对应的系统参数a、b。

最后，根据上述步骤中获取的个体适应度，采用轮盘赌的方式选择优良的个体，然后进一步通过交叉、变异等操作形成新的种群。并设定最大迭代次数，当满足条件时，终止循环，并将系统每一个特征的独立通道计算的最大输出PSNR 对应的系统参数a、b，作为各自独立通道FHN 神经元随机共振系统的最优参数。

2 实验结果及分析

本文所有的实验均在Ubuntu 20.04 LTS 版本上安装MATLAB R2016b 版本进行实验，主要硬件包括AMD Ryzen 5 5600H 的CPU 和16GB 的内存。另外，本文以本实验室基于常规微生物学实验需要而采集的菌落图作为实验对象，采用仿自然光悬浮式暗视野系统，以F/1.4 大光圈镜头，对培养后皮氏培养皿上所生长的菌落进行了千万像素级的成像。

本实验从采集的菌落图像中，随机挑选5 张菌落图分别命名为Colony_1、Colony_2、Colony_3、Colony_4 和Colony_5，然后分别使用全局直方图均衡化、低通滤波、单尺度Retinex、多尺度Retinex 以及本文提出的图像增强算法在随机挑选的5 张菌落图上进行实验，菌落图增强实验结果如图4 所示。其中，第1 行为菌落实验原图；第2 行为全局直方图均衡化菌落增强结果图；第3 行为低通滤波菌落增强结果图；第4 行为单尺度Retinex 算法菌落增强结果图；第5 行为多尺度Retinex 算法菌落增强结果图；第6 行为本文算法菌落增强结果图。

图4 菌落示意图

通过对菌落图实验结果的直观观察，可以发现利用全局直方图均衡化对Colony_1～Colony_5 实验菌落图像进行增强处理后，增强图像具有更高的对比度，图像锐化效果比较突出，但这也会导致图像背景发生较大的失真，丢失部分原图像的背景信息，细节信息缺失，增强后的菌落图像颗粒感明显，噪声无法得到有效的抑制。低通滤波算法增强处理后的结果相对原图的边缘细节部分变得模糊，甚至部分小的细菌会被当成噪声滤除了，这种现象在Colony_1 和Colony_2 这种细节信息丰富的菌落图像中是比较明显的，同时也可以发现，经过低通滤波后增强的图像菌落和背景图之间的对比度没有得到有效的改善。单尺度Retinex算法则会导致菌落图像目标区域与背景区域的对比度下降，增强后的菌落图像细节部分不突出，整体看起来菌落图像增强效果不够明显。多尺度Retinex 算法对于菌落图虽然有比较好的增强效果，但增强之后的图像失真比较严重，会有比较明显的灰度化现象出现，破坏了原有图像的色彩结构。本文提出的方法不仅能较好地保持原有图像的色彩结构，同时对于细节的重构也是比较理想的，不仅提高了菌落和背景的对比度，还能很好地解决了灰度化现象的问题。

另外，为了更好地对不同算法的增强结果进行量化分析，本文采用在图像质量评价方面比较有统一性的PSNR 值作为定量评价的依据，具体结果如表1 所示。通过对Colony_1～Colony_5 实验菌落图上不同增强算法实验结果的分析，可以发现全局直方图均衡化和单尺度Retinex 图像增强算法的稳定性和鲁棒性是比较差的，对于不同的实验对象，PSNR 值波动较大，全局直方图均衡化增强细节比较丰富的Colony_1 和Colony_2 菌落图像时有一定不足，而单尺度Retinex 算法则与全局直方图均衡化有所不同，受限于尺度单一的限制，它对Colony_3、Colony_4 以及Colony_5 等相对于Colony_1 和Colony_2 细节较少的图像表现比较差。多尺度Retinex 增强算法则解决了单尺度Retinex 算法尺度单一的缺陷，在Colony_1～Colony_5 实验菌落图上具有比较好的表现。另外，可以发现低通滤波、多尺度Retinex 以及本文提出的基于FHN 神经元自适应的多通道随机共振图像增强算法，面对不同的实验对象都具有比较稳定的表现，这也证明算法具有很强的鲁棒性，可以适应不同实验环境。同时通过对比，也可以明显直观地发现对于相同的实验对象，本文的实验结果是要远远优于其他算法的，如图5 所示，这也证明本文算法的有效性和实用价值。

表1 菌落图在不同图像增强算法下的PSNR 值

图5 增强算法的PSNR 值实验结果可视化

同时本文对不同算法在图像平均检测处理速度上进行了统计，如表1 所中的每秒处理帧数(Frames Per Second，FPS)指标所示，根据实验结果显示，本文方法虽然相对于低通滤波这种直接滤波处理速度较慢，但其PSNR 值是有较大优势的；另外，根据实验结果对比分析，本文方法在处理速度上和增强效果上都是优于全局直方图均衡化、单尺度Retinex、多尺度Retinex 等方法的。这也进一步证明了本文方法在图像增强方面的实用性和有效性。

为了进一步阐述本文所提方法在图像去噪方面的优越性和一般性，本文随机选取三幅低剂量CT脑部图像，从图像中可以看出由于噪声的干扰，原始图像整体显示比较暗淡，轮廓与背景的对比度差异性不明显。

图6 是对三幅含噪图像采用单尺度Retinex、多尺度Retinex 以及本文提出方法的处理结果图，通过实验结果的对比分析，可以看到单尺度Retinex 很难去除较大强度的噪声，而且经过滤波还会对图像产生模糊的作用，这样不利于观察图像中的细节信息。通过多尺度Retinex 方法处理获得的CT 脑部图像增强结果图，可以发现对噪声可以产生一定的屏蔽作用，同时可以增强图像整体亮度，但是对于噪声强度较大图像的增强效果并不是很好。而本文提出的基于随机共振的方法可以很好地处理噪声，并利用噪声的特点将其与图像信息有机统一，最终达到增强图像的目的，这一点也可以从图中看出，经过增强处理之后的图像几乎没有颗粒噪声的存在，所以从图像上看起来目标区域与背景区域对比度较为明显，而且能很好地实现噪声能量的转化，改善了传统方法在图像处理时细节模糊的不足，最终提高了图像的增强效果。

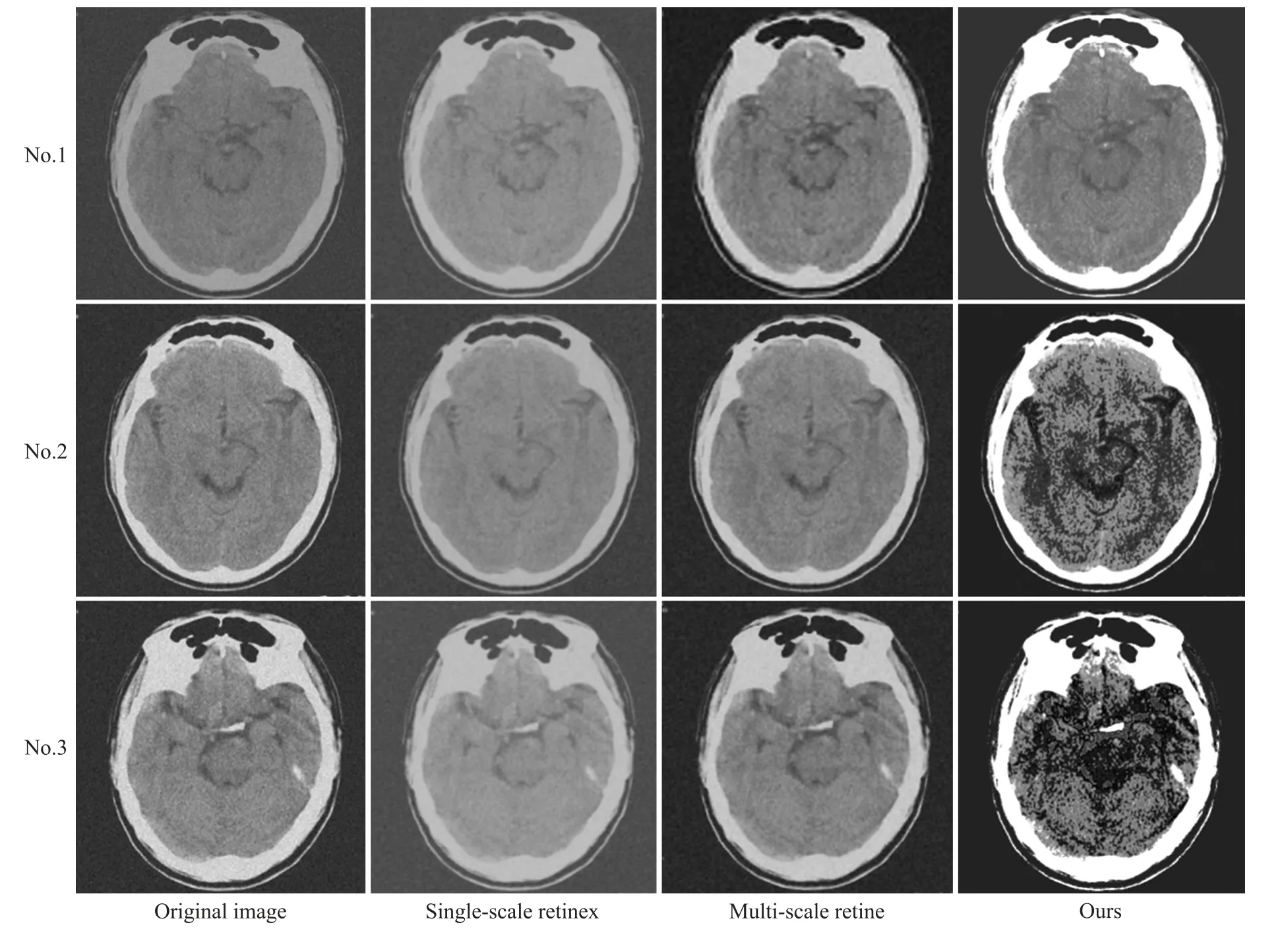
图6 不同增强算法的低剂量脑部CT 图实验结果

鉴于图像信息熵是图像质量评价的常用指标，它从信息论的角度反映图像信息丰富程度。通常情况下，图像信息熵越大，其信息量就越丰富，质量越好。因此为了便于更好地说明本文提出方法的有效性，本文计算低剂量脑部CT 图增强实验结果的信息熵值，如表2 所示，从表中实验结果可以发现，对于随机选取的三幅图像，本文方法的信息熵是要优于另外两种方法的，三种方法的信息熵分别为6.638 4、6.377 9、6.539 3，这也直接表明，本文方法在对低剂量脑部CT 图处理时，可以获得更多的图像细节和图像轮廓对比度。

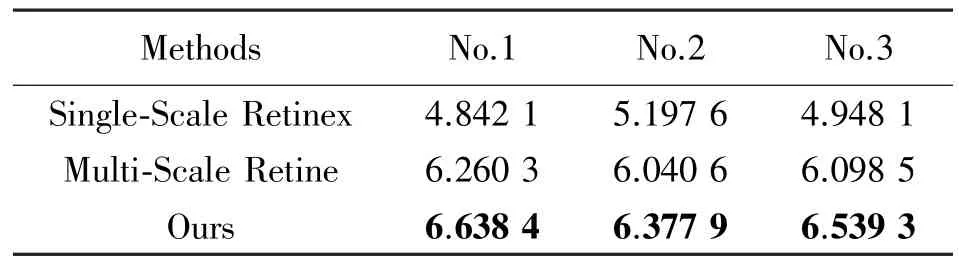
表2 不同增强算法实验结果信息熵值

为了证明本文方法的有效性，进一步对实验结果进行像素分布范围统计，本文利用了直方图对不同实验方法图像增强结果进行分析对比，如图7 所示，可以直观地发现本文提出方法的像素等级分布，相对于单尺度Retinex 方法、多尺度Retinex 方法是更加广泛和均衡的。另外，单尺度Retinex 方法图像增强之后的直方图分布是比多尺度Retinex 方法要狭窄的，这个结果也与表2 中的信息熵计算结果相符。

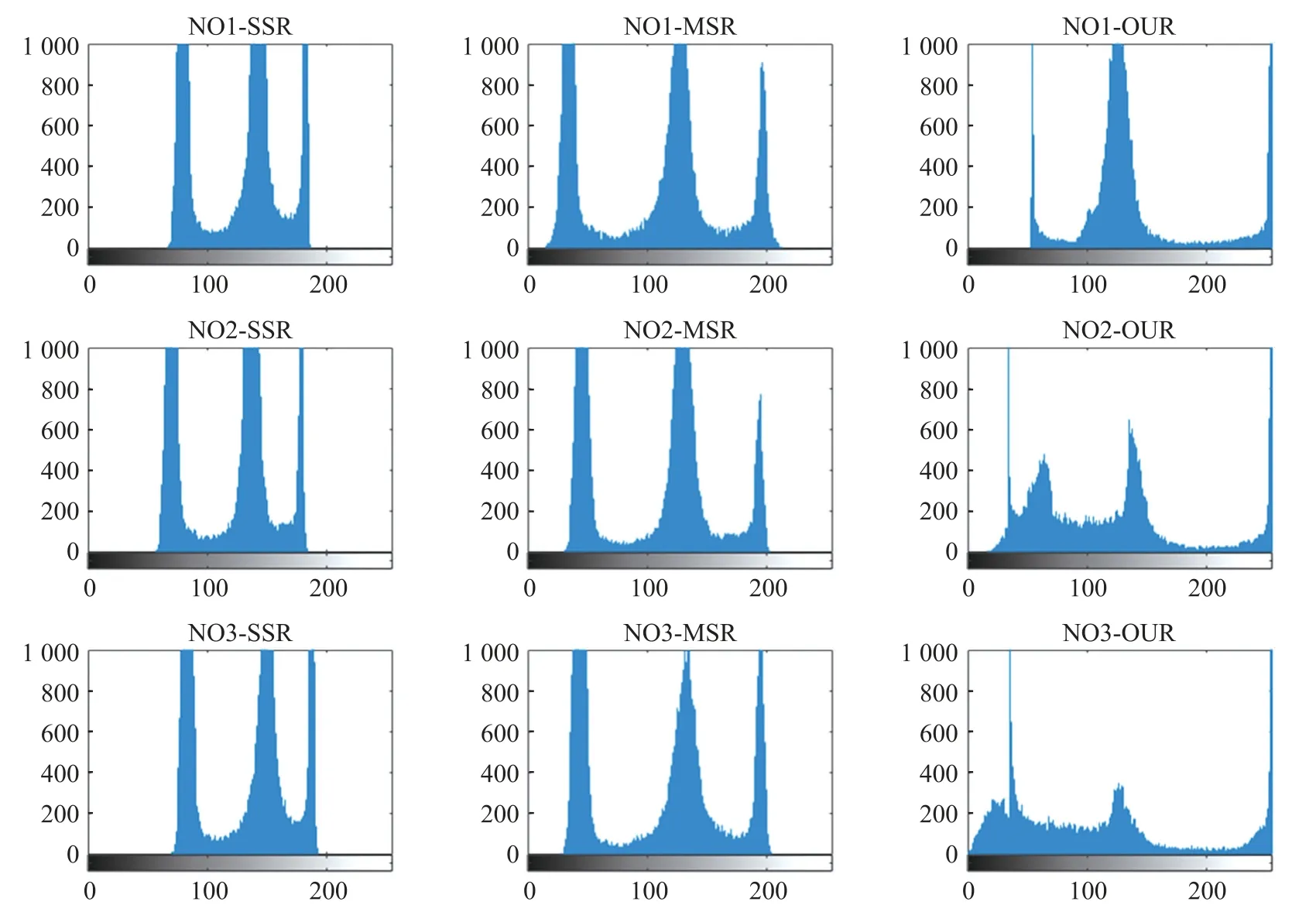
图7 低剂量脑部CT 图不同方法增强结果直方图

4 总结与展望

本文提出利用基于遗传算法优化的FHN 神经元模型的自适应多通道随机共振机制实现弱信号的增强算法，提高受到噪声干扰的图像质量。本文提出的与传统增强方法抑制噪声的思路是截然不同的，主要利用非线性FHN 神经元、图像信号以及噪声之间的共振协同作用，使噪声能量向图像信号能量实现转移，从而对受到噪声干扰的菌落图像实现增强效果。实验结果表明，本文方法在菌落图的对比度提升以及图像细节增强方面，相对于传统算法具有更好的实验效果。因此，对基于遗传算法优化FHN 神经元模型的自适应多通道随机共振机制实现弱信号增强算法的研究为图像增强处理提供一种更加新颖的思路。