基于改进A*＋RDP 算法的无人艇回坞路径规划方法*

张美燕，杨庆生，蔡文郁*

(1.浙江水利水电学院电气工程学院，浙江 杭州 310018；2.杭州电子科技大学电子信息学院，浙江 杭州 310018)

无人艇(Unmanned Surface Vessel，USV)[1]具有广泛的应用前景，在科研、环境监测、军事用途、资源勘探和巡逻搜救等领域，无人艇已经成为国内外海洋装备的研究热点。无人艇一般随母船执行任务，因此要求具备快速作业与安全回坞的能力。高效可靠的无人艇收放技术可以提高海上作业的效率[2]，图1 所示为母船尾部外挂喇叭口状桁架式回收坞方案，外挂式回收坞和母船的连接形式为柔性连接，即在母船两侧锚机和中间的拖带绞车，共三根缆绳固定回收坞三个固定点，依靠无人艇自动回坞就可以实现无人艇的安全回收。

图1 无人艇回收坞结构示意图

目前关于无人艇自动回坞技术的研究不多[3-4]。2014 年，Joel 等[3]采用三维激光雷达实现对回坞码头建图识别，应用于小型无人水面舰艇的自动回坞，但是具有三维激光雷达成本较高、点云数据建图耗时过多等缺陷，因此不适用于动态回坞场景。2018 年，Yilmaz 等[4]研究了基于视距(Line of Sight，LOS)和纯追踪(Pure Pursuit，PP)的自动回坞导引策略，并提出优化模型预测控制器(Model Predictive Controller，MPC)和级联PID 控制器的参数来优化无人艇的路径跟随性能。

除此之外，无人艇自主回坞的关键是要解决复杂海况下的路径规划问题[5-6]。无人艇的路径规划方法主要划分为全局路径规划、局部路径规划和混合路径规划等几种。基于搜索的全局路径规划方法将无人艇视为无动力学约束的质点，仅考虑空间约束，相关的研究比较成熟。具有代表性的路径规划方法——A*搜索算法[7]通过构建合适的启发式函数，使得搜索过程往代价值更小的方向搜索，兼顾搜索效率和路径质量。随机采样搜索算法RRT*(Rapidlyexploring Random Tree)[8]能够快速找到可行的路径，但是随机采样特性导致路径质量不高。2006 年，Larson 等[9]将A*搜索算法用于无人艇的避障路径规划，在有限的时间内搜索最佳路径；2014 年，Kim 等人基于改进的A*算法，即在A*算法的代价函数中增加曲率半径代价，规划更合理的无人艇路径[10]。2019 年，Song 等[11]提出了一种改进的A*算法，结合路径平滑算法规划路径，并于Springer 号无人艇验证可行性。在路径规划的基础上，考虑运动学和动力学等约束，如速度、方向、旋转角速度、旋转半径(曲率)等，从而规划出无人艇回坞的具体轨迹。

本文针对无人艇回坞路径规划问题，提出全局路径搜索和轨迹生成相结合的路径规划方法，使用改进的A*启发式搜索算法和拉默-道格拉斯-普克算法(Ramer-Douglas-Peucker，RDP)[12]计算全局路径点，满足无碰撞和艏向约束；考虑无人艇的运动学参数、轨迹连续性约束，采用贝塞尔曲线构建生成推力变化率(Snap)[13]最小的规划路线，满足安全回坞的需求。

1 基于改进A*＋RDP 算法的自动回坞路径规划

传统的路径规划算法一般将路径长度作为优化目标之一，即航迹的路径总长度L(p)，本文也将航迹总长度作为优化目标之一[14]。无人艇在回坞阶段需要与移动的回收坞进行对接，为了避免发生碰撞，保证船体和被救援人员的安全，无人艇控制系统必须保证推进力变化平滑，不存在推进力的突变。本文将总轨迹的Snap 值之和最小(即无人艇的推力变化率最小)也作为优化目标，因此本文研究的自动回坞路径规划优化目标如下所示:

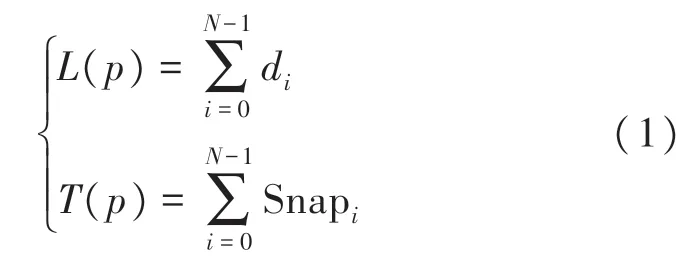
式中，p表示路径规划算法得到的参考轨迹函数，di表示第i段航迹的长度，N段航迹组成的总轨迹长度为L(p)，Snapi表示第i段航迹的加速度变化率，N段航迹的Snap 总和为T(p)。

基于改进A*＋RDP 算法的自动回坞路径规划主要流程如图2 所示，主要包括栅格地图生成、全局路径规划、RDP 算法优化、轨迹曲线插值等四个部分。将自动回坞区域的电子海图生成栅格地图数据，输入A*全局路径规划算法获取避障安全路径，然后采用RDP 算法简化路径点，降低计算复杂度，最后采用曲线插值方法输出平滑路径导引回坞任务。

图2 自动回坞路径规划流程图

1.1 栅格地图生成

无人艇路径规划首先需要对环境进行建模，因为船载电子海图包含了岛屿、礁石等海上障碍物信息，本文直接采用电子海图生成路径规划所需的栅格地图。电子海图模型采用地理坐标系统，不便于直接进行路径规划，采用墨卡托投影方法[15]将地图信息的经纬度转换为米制单位，转换公式如下所示:

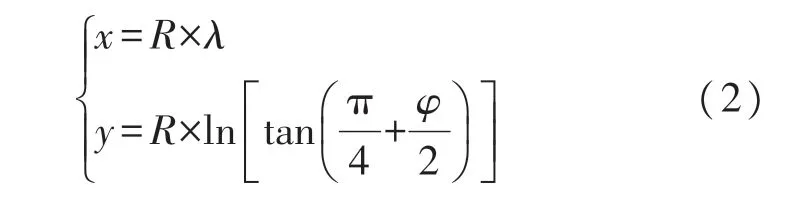
上式表示经纬度坐标(λ，φ)对应的米制投影坐标为(x，y)，R表示地球半径。经过墨卡托投影转换，地图信息的经纬度统一转换成米制单位。除此之外，电子海图中的静态障碍物也需要映射到栅格地图中。在实际工程中，栅格地图以二维数组形式保存，每个栅格点处，障碍物区域对应数值为255，非障碍物区域数值为0。按上述方法进行栅格化处理，原始电子海图如图3(a)所示，处理后的栅格地图如图3(b)所示。

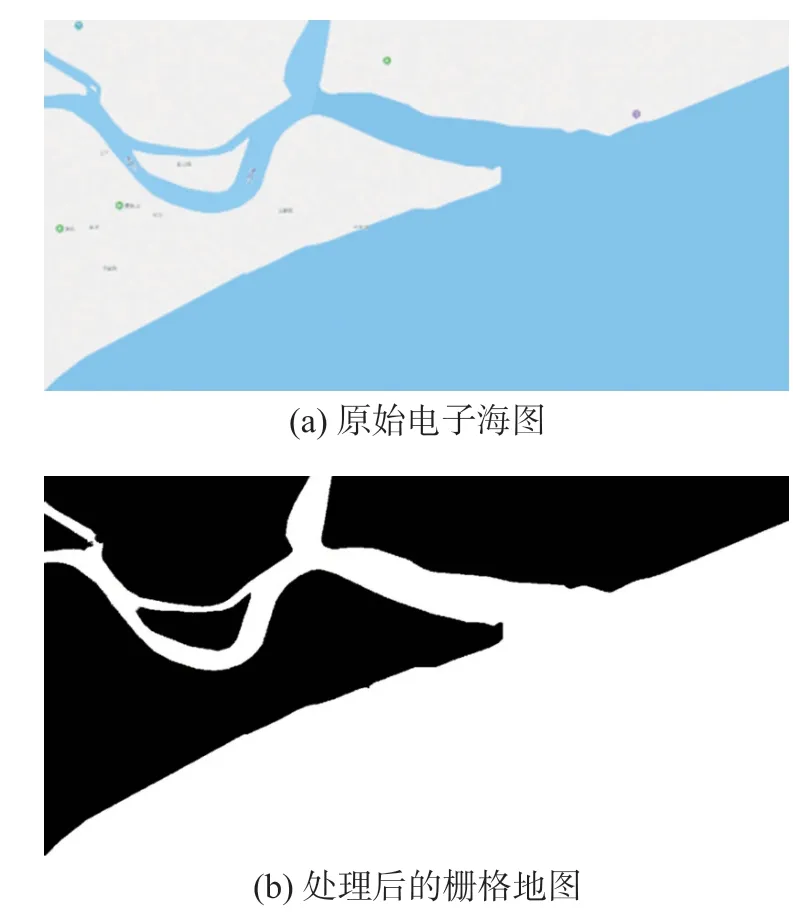
图3 地图处理示意图

1.2 全局路径规划

全局路径规划的目标是在离散的栅格化地图，规划出一条满足碰撞约束、艏向约束、安全距离约束的无人艇路径。本文以A*算法作为全局路径规划算法的基础，研究以无人艇为规划对象的A*改进算法。传统的A*算法节点搜索策略将规划对象视为质点，不考虑规划对象的运动学约束，节点搜索方向为邻近的8 个栅格，即规划对象不受转向约束，节点搜索示意如图4(a)所示。本文的研究对象为无人艇，搜索策略应该考虑无人艇的艏向，并根据其转向角度限制范围进行搜索，考虑约束的搜索示意如图4(b)所示。除此之外，传统的A*算法不考虑规划对象的物理尺寸和安全距离约束，但是无人艇在海上行驶，应遵守安全距离约束，如图4(c)所示，需考虑横向安全距离和纵向安全距离。

图4 改进A*算法工作原理

A*算法中每个节点都存储了自身的键值f，键值决定了节点在访问列表中的优先级，键值越低意味着代价越小，访问优先级高。节点n的键值计算表达式f(n)如下式所示:

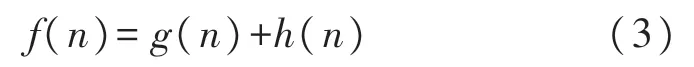
式中，g(n)为节点n到起始点的距离，h(n)代表搜索的启发式函数。本文使用节点到目标点的欧氏距离作为启发式函数，如下式所示:

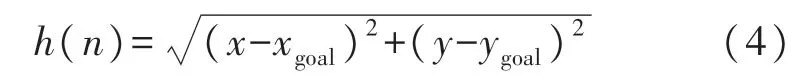
式中，(x，y)代表当前点坐标，(xgoal，ygoal)代表目标点坐标。

本文研究的A*改进算法主要包括以下两方面:

①启发式函数h(n)改进

采用欧氏距离作为启发式函数时，如果当前节点位置下无人艇的偏航角并不是朝着目标节点，此时的代价估计值应该更大，也就说欧氏距离并不能反映出无人艇艏向角度的影响。本文在启发式函数基础上额外考虑了艏向角偏差的加权值，如下式所示:

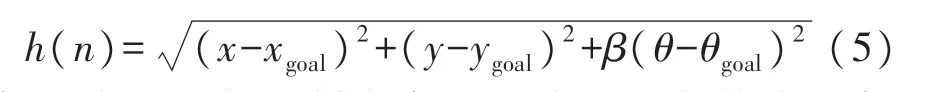
式中，θ为无人艇的艏向角，θgoal为无人艇指向目标点的艏向角，β为权重因子，取值0.2。基于改进后启发式函数的A*算法原理示意如图5 所示。

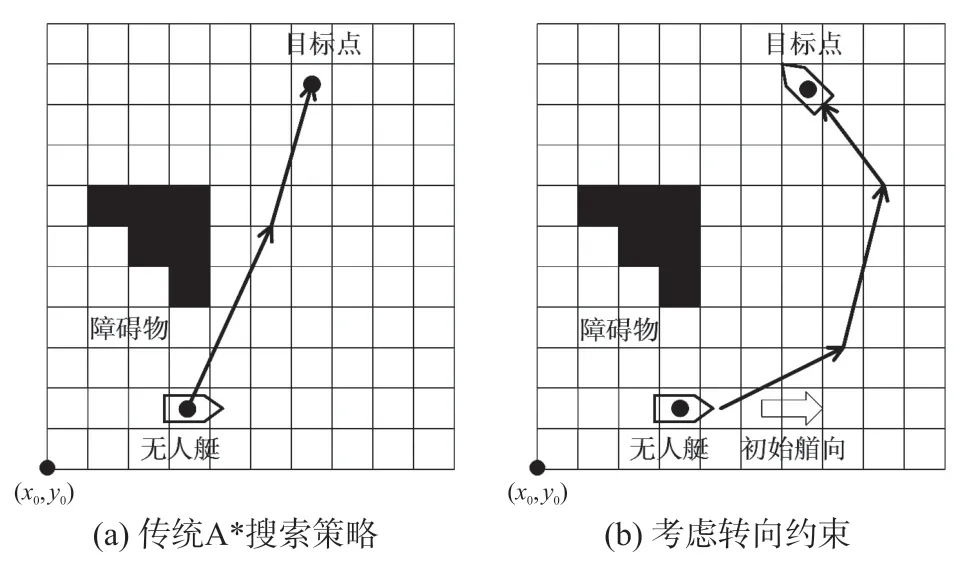
图5 改进启发式函数算法原理

②安全避障约束改进

如图6(a)所示，在传统的A*搜索策略中，只有当路径点完全处于障碍物的坐标点时才判定为不可通行，这与实际情况并不相符，因此需要额外考虑安全约束。如图6(b)所示，当前节点向邻节点拓展搜索时，邻节点向周围的横向安全距离D和纵向安全距离L范围可到达的节点进行障碍物判断:若有障碍物，则标记该邻节点为不可通行，否则，标记为可通行。

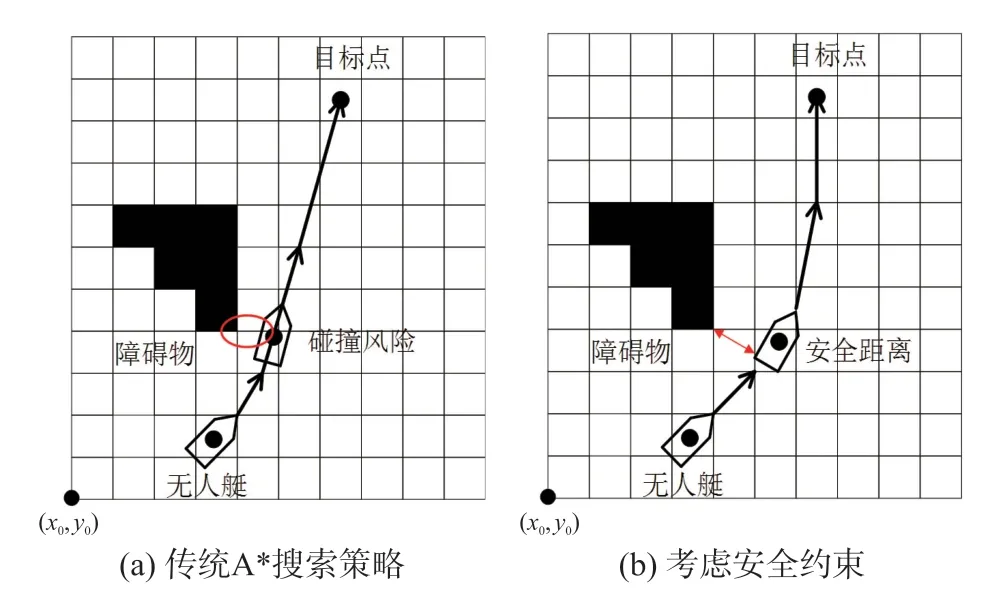
图6 考虑安全约束的搜索策略

1.3 RDP 算法优化

栅格地图的精度越高，路径中包含的离散路径点数越多，但是过多的路径点产生了矢量特征的冗余。拉默-道格拉斯-普克(RDP)矢量数据压缩算法可以用较少的矢量数据保留原始矢量数据的特征。原始轨迹经过RDP 算法优化的路径点保留了原始路径的基本轮廓，但是减少了路径点。因此，本文结合RDP 算法对全局路径进行简化，减少中间路径点、增加直达点。

1.4 轨迹曲线插值

改进A*算法规划的全局路径是由直线段构成的路径，不适合直接作为无人艇的参考航迹，因此需要进行平滑处理。本文利用Bezier 曲线[16]的凸包性质和导数性质，通过控制点约束各阶Bezier 曲线，实现对各阶轨迹施加不等式约束。伯恩斯坦形式的Bezier 曲线表达式如下:

以最小化总体轨迹的Snap 值之和为优化目标，将每段Bezier 曲线的时间取值归一化到[0，1]区间，总路径轨迹的Snap 值之和为:

式中，τ∈[0，1]，pi＝[pi0，pi1，pi2，…，pin]T为第i段Bezier曲线的多项式系数向量，Qi为对应第i段曲线的Q矩阵:

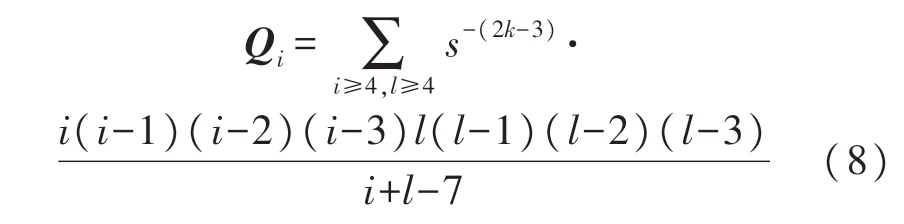
因此，基于全局路径点的Bezier 曲线参数求解问题可转化为如下约束优化模型:

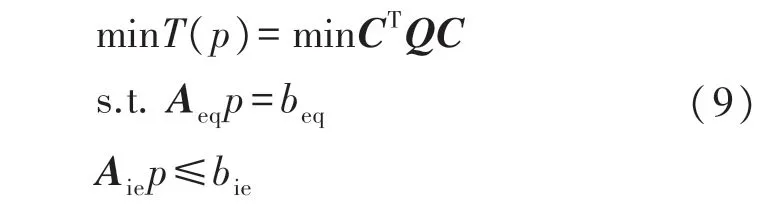
式中，C为Bezier 曲线系数组成的向量，Aeq为等式约束矩阵，Aie为不等式约束矩阵，beq和bie分别是等式约束值和不等式约束值。Bezier 曲线的参数求解问题，转化为二次规划(Quadratic Programming，QP)问题[17]。为满足该模型的参数变量求解，本文取n＝7 阶Bezier 曲线。由于航迹必须通过全局路径规划的各路径点，还需满足起始航速、起始加速度等约束，构建等式约束矩阵如下所示:

式中，j表示第j段轨迹，l表示阶次，μ表示分量，为归一化系数表示起始点组成的向量表示l阶的第i个控制点，定义如下:

除此之外，在各段Bezier 曲线的连接处必须满足各阶连续性约束，即两段曲线的连接处的位置、航速和航速加速度保持连续，如下所示:

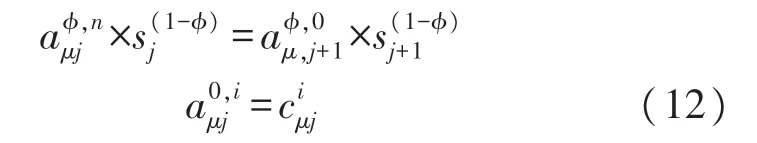
等式约束保证了航迹满足连续性约束，不等式约束保证航迹满足运动学参数的约束。本文的运动学约束主要考虑无人艇的航速和加速度约束，如下所示:

式中，v为无人艇航速，a为无人艇加速度。根据式(10)、式(12)和式(13)，将多段轨迹的约束写成矩阵形式，代入等式约束矩阵Aeq和不等式约束矩阵Aie，式(9)所示的QP 问题可通过拉格朗日等经典方法[17]求解，求解每段轨迹的Bezier 曲线参数，最终得到平滑的回坞轨迹。

2 仿真结果

为了验证本文算法的性能，选取了广东省阳江市阳江港口的实际电子海图场景，经度111.809 046 294 04，纬度21.712 751 661 48，利用MATLAB 软件编程实现算法仿真。无人艇回坞路径规划主要参数设置如表1 所示。

表1 无人艇路径规划仿真参数

为了对比A*、RRT*、改进A*＋RDP、改进RRT*＋RDP 等算法性能，包括路径质量(路径长度、路径点数量)和算法效率(算法执行时间)，不同起点和终点条件下的仿真结果如图7～图10所示。

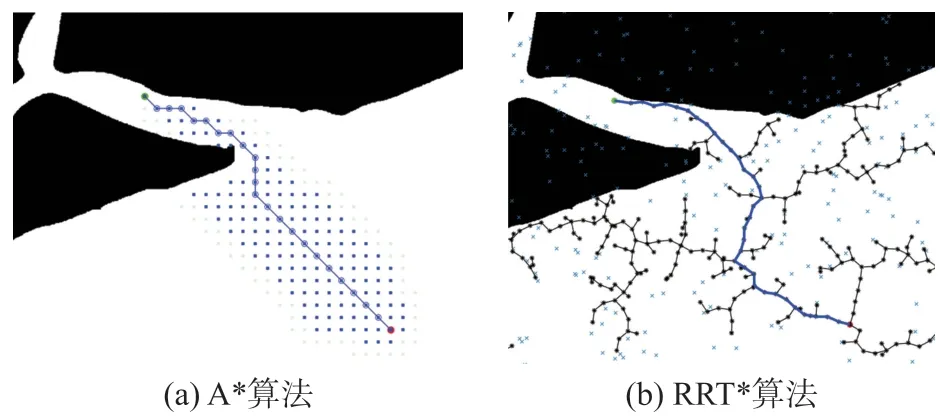
图7 A*和RRT*算法仿真对比(场景1)

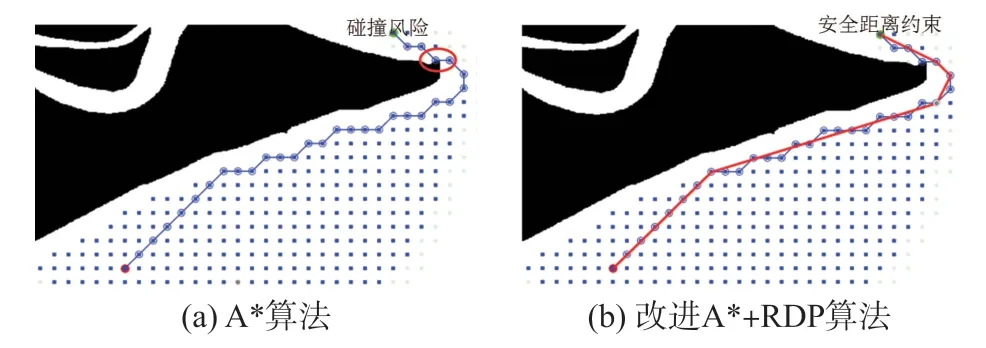
图8 A*算法仿真对比(场景2)

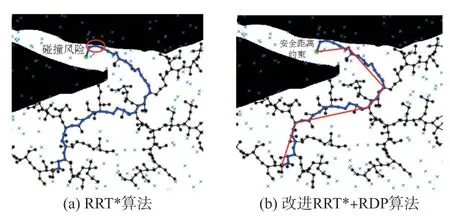
图9 RRT*算法仿真对比(场景3)

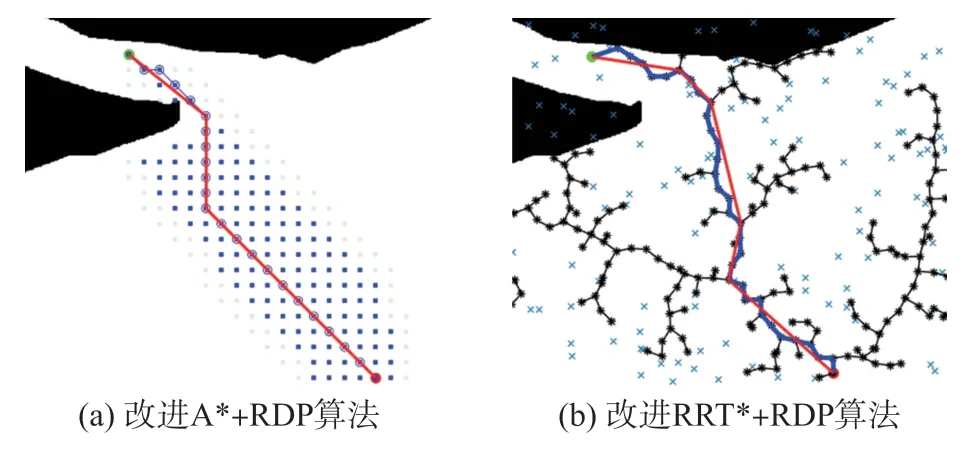
图10 改进A*和RRT*算法仿真对比(场景4)

通过多次仿真取均值，A*算法、改进的A*与RDP 结合算法、RRT*算法、改进RRT*和RDP 结合算法四种算法的数值结果对比如表2 所示。

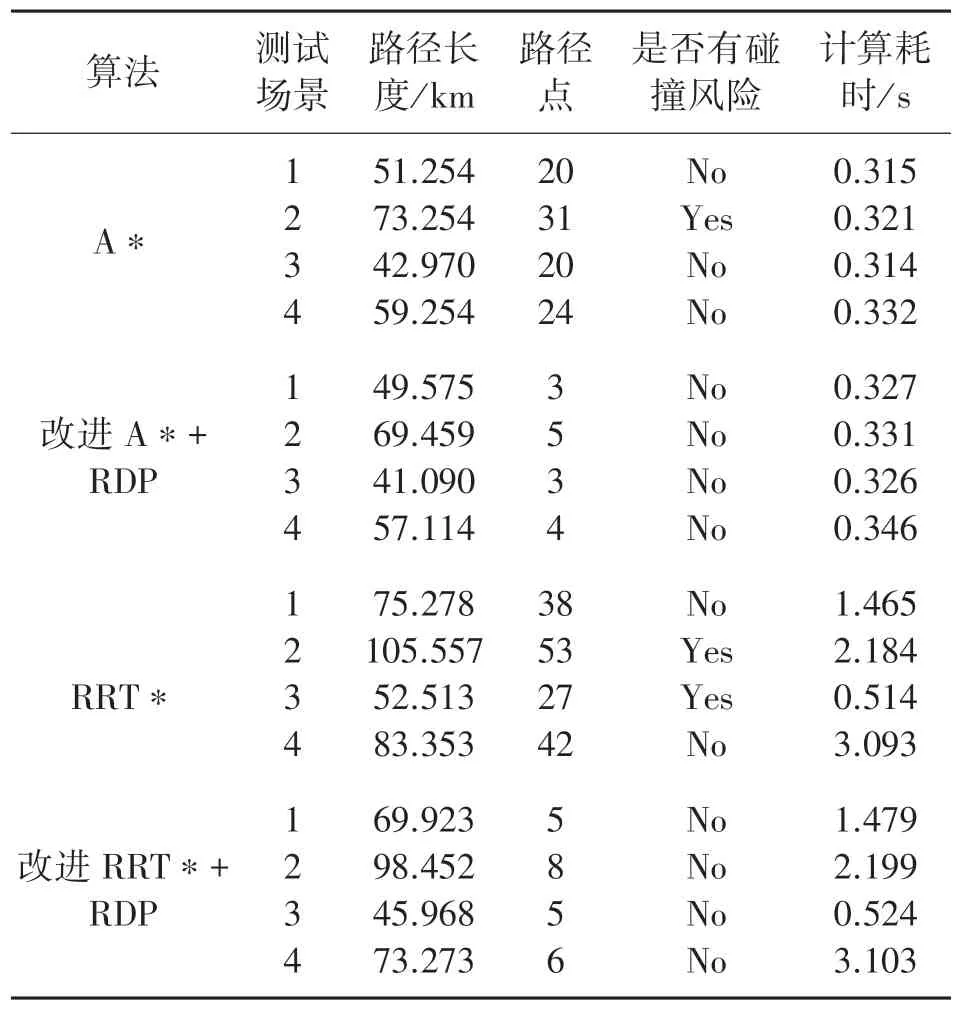
表2 对比算法仿真结果

从表2 可见:①A*算法规划的路径长度比RRT*算法更短；改进的A*＋RDP 算法相比原始A* 算法的路径长度下降约4%，改进的RRT*＋RDP 算法相比原始RRT*算法的路径长度下降约9%；②A*算法的路径点数量少于RRT*算法的路径点数量，改进后的A*＋RDP 算法和RRT*＋RDP算法，路径点数量下降约84%。上述实验结果表明，RRT*算法的路径随机性大、质量差，容易生成弯折的路径，且有碰撞风险，不利于后端的轨迹生成。改进后的A*＋RDP 算法相较于传统A*算法，增加了艏向约束和安全距离约束，无碰撞风险，同时更接近路径较短的优化目标。

轨迹曲线插值的仿真结果如图11 和图12 所示，蓝色栅格点为A*搜索算法搜索过的区域，图11(a)和图12(a)为A*算法的路径，可见A*算法在全局搜索阶段得到一条无碰撞路径；图11(b)和图12(b)为经过RDP 算法优化的路径，RDP 算法减少了A*路径的弯折，减少了路径点数量；图11(c)和图12(c)为基于Snap 值最优的多项式轨迹，生成的轨迹经过RDP 算法的所有路径点，而且轨迹间连接平滑。

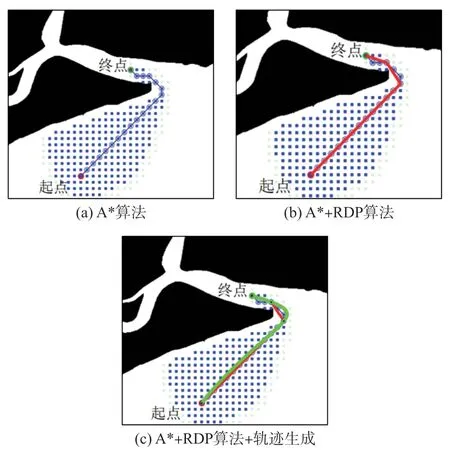
图11 轨迹曲线插值仿真结果(场景1)

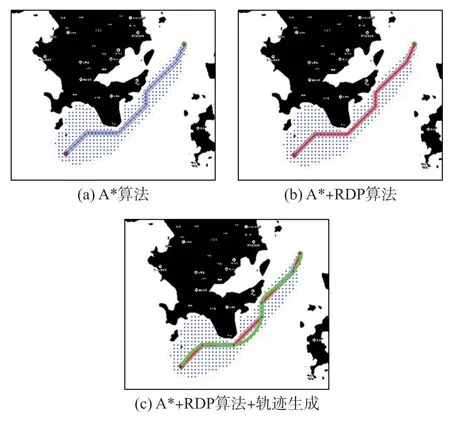
图12 轨迹曲线插值仿真结果(场景2)

图11 和图12 的仿真结果数据如表3 所示。从表3 可以看到，使用A*算法生成路径点，然后生成贝塞尔轨迹，计算耗时最多，主要是因为A*算法生成的冗余路径点较多，轨迹生成算法求解多段曲线的参数，计算效率较低。改进的A*＋RDP 算法生成路径点，再生成贝塞尔轨迹，在两种场景下的计算效率提高了约9%～13%。因此，验证了本文提出的改进A*＋RDP 算法可以减少冗余的路径点，提高轨迹生成算法的计算效率。

表3 仿真结果数据

3 结语

本文通过分析无人艇回坞路径规划的优化目标和约束条件，提出了一种全局路径规划和轨迹生成算法相结合的无人艇回坞路径规划算法。以改进A*搜索算法为基础，结合RDP 算法优化路径点数量，以路径长度和Snap 最小为优化目标，生成平滑Bezier 曲线轨迹。仿真结果验证了本文提出的改进A*和RDP 算法对全局路径的优化效果，说明基于多约束优化模型生成Bezier 曲线作为无人艇回坞路径具有可行性。