基于改进时频共空间模式的运动想象脑电信号分类*

范凌霄，高云园，2*，马玉良

(1.杭州电子科技大学自动化学院，浙江 杭州 310018；2.浙江省脑机协同智能重点实验室，浙江 杭州 310018)

脑机接口(Brain Computer Interface，BCI)是指将人或动物大脑与计算机或其他外围设备直接连接，并实现控制和通讯的方法。BCI 的研究可以帮助患者，通过脑电信号直接与外部世界进行通信[1]。由于脑电信号(Electroencephalogram，EEG)具有无创性、良好的时间分辨率和方便性，长期以来一直受到了很多学者的关注[2]。脑机接口的实现在很大程度上依赖于对脑电信号的分类[3]。

由于EEG 信号具有非平稳、低信噪比、多通道的特性，一些时域和频域特征处理方法如自回归模型[4]、双谱分析法[5]等效果较差。时频域特征处理方法如小波包变换[6]、经验模态分解[7]等能有效提取不同节律的时变和瞬时特征，解决了脑电信号时变性的问题，但是仍然存在对多通道脑电数据适应度低的问题。共空间模式(Common Space Pattern，CSP)[8]通过组合来自所有可用记录通道的信号，从空域角度寻找EEG 信号的投影方向，使任意两类EEG 信号之间的差异最大化(即找到一组权重向量，最小化一类方差的同时，最大化另一类的方差)。

虽然传统的CSP 在脑电信号运动想象分类中取得了一定效果，但空间滤波器的性能往往取决于工作频带、脑电通道和时间窗口的选择。每个受试者的最佳工作频带都是不同的，在一个固定的频带上使用CSP 方法难以获得很好的EEG 分类性能。滤波器组共空间模式(Filter Bank Common Space Pattern，FBCSP)将EEG 信号滤波到多个频带并从中提取特征，并通过互信息对特征进行自动选择，提高了分类准确率[9]。传统的CSP 方法采用了所有的可用信道，由于通道间存在冗余信息和噪声干扰，使用全部的通道信息并非对分类有利，研究人员提出了许多算法来对通道进行选择。Arvaneh M 等[10]提出了稀疏CSP (Sparse Common Space Pattern，SCSP)方法，通过在CSP 优化函数中加入L1 和L2范数约束对过滤器进行稀疏，去除与运动想象(Motor Imagery，MI) 无关的冗余通道。Tam WK等[11]提出了一种基于空间滤波器排序的CSP-Rank算法，通过观察滤波器系数的大小选择通道。除了滤波器频带优化和通道选择以外，另一个重要的问题是为脑电信号选择合适的时间窗口。Miao Y等[12]认为每个受试者在运动想象过程中事件相关去同步(Event-Related Desynchronization，ERD)的时间进程是不相同的，提出了一种时频空间滤波框架，将整个MI 周期分成多个候选时间窗，在每个时间窗上提取多个频带，从而更好地挖掘脑电信号中的信息。此外，有研究人员结合通道筛选和子频带划分提出一些改进算法。CSP 多频带滤波器排序及信道选择方法(CSP-Rank Channel Selection for Multifrequency Band EEG，CSP-R-MF)将信号分解到多个频带后，对每个频带利用CSP-Rank 算法减少冗余通道[13]。孟明等[14]提出了块选择共空间模式(Block-Selection for CSP，BS-CSP)，利用Fisher 比对通道和频带同时进行选择。

现有的一些方法都是通过结合通道选择和多频带划分，解决了传统CSP 方法存在的问题。然而他们都是在固定的时间窗口上，没有对时间窗进行选择。并且仅采用特征选择算法从各子频带特征集合中提取稀疏CSP 特征，没有对子频带进行选择，导致算法分类性能的下降。本文系统地将频带、通道和窗口的选择与传统CSP 方法进行结合，提出了一种通道选择共时频空间模式(Channel selecting for common time-frequency-space patterns，CS-CTFSP)的新框架。首先利用皮尔逊相关系数计算通道间相关性，在主通道的基础上筛选出合适的通道集合；之后从多个候选时间窗口内划分多段子频带，并利用时频共空间模式提取特征；接着引入能量和特征值两个指标，对频带进行筛选后提取稀疏的CSP 特征；最后采用LDA 分类器进行分类。本文的主要创新和贡献为:①提出了新的通道选择方法，将主通道筛选和相关性分析应用到通道选择；②利用能量和特征值对EEG 子频带进行筛选，实现特征筛选。

本文的结构如下:在方法部分描述了框架的细节并介绍了本文所使用的算法。在实验部分介绍了使用的两个公开数据集和通道阈值设置方法。结果与分析部分列出了实验结果并对其进行了分析。最后在结论部分对全文进行了总结，并讨论了未来的改进方向。

1 方法

1.1 整体框架

由于EEG 本质上是一个非平稳的时间序列信号，传统共空间模型存在不能充分利用信号的频带和时间域信息，并且无法解决通道冗余的问题。本文通过相关系数去除冗余通道后，对每个时间窗的子频带进行选择，从而提高CSP 特征表征运动想象的能力。本文提出CS-CTFSP 结构框图如图1 所示。首先通过计算其他通道与主通道间皮尔逊相关系数对通道进行选择；然后对整个MI 周期进行子时间窗分割，在每个时间窗内，通过5 阶巴特沃兹滤波器提取mu 和beta 子频段；之后利用CSP 算法提取每个子窗口的频带特征；筛除低能量和低特征值的子频带单元后利用LASSO 进行特征降维选择；最后将所得特征经过融合后送入LDA 分类器分类。

图1 CS-CTFSP 方法的总体框架

1.2 通道选择

K个通道的脑电信号，一共进行M次试验。第i次试验，第k个通道的脑电信号为:，这其中k＝1，2，…，K，i＝1，2，…，M，N是每个脑电通道的采样点数。

皮尔逊相关系数是一种量化两个或多个随机变量之间统计关系或线性相关性的一种度量，其定义如下式(1):

式中，X和Y是两个可观测变量，ρXY的取值范围是[0，1]，其值越大，则表明X与Y相关度越高。本文采用皮尔逊相关系数衡量脑电通道之间的相关性。

在基于脑电信号的运动想象通道选择中，通常选取运动感觉区域的Cz(大脑皮层中央区域)，C3(大脑皮层左侧区域)和C4(大脑皮层右侧区域)通道[15-16]。本文将这三个通道作为主通道，利用皮尔逊相关系数衡量两个通道之间的相关性，进而选择与主通道相关性高的通道作为其拓展通道。

本文每次试验都计算三个主通道与其他所有脑电通道间的相关系数，构成一个3×K维的相关系数矩阵C，其中元素cij，i＝1，2，3，j＝1，2，…，K表示第i个主通道与第j个通道间的相关系数。计算相关系数矩阵C中每列的和，得到1×K维行向量，并对其进行降序排列，记录排序后向量的前Ms个元素，在M次试验后得到M×Ms维通道排序矩阵，将其中出现频率最高的前Ms个通道作为主通道的拓展通道。通道选择算法的伪代码如表1 所示。Ms是通道选择中的重要参数，通过交叉验证确定。

表1 通道选择伪代码

1.3 窗口和频带划分

由于运动想象实验中事件相关的去同步/同步现象(ERD/ERS) 主要出现在mu 频段(8 Hz～13 Hz)和beta 频段(14 Hz～30 Hz)，因此利用8 Hz～30 Hz 的5 阶巴特沃兹滤波器提取与运动节律相关的主要频带。此外，每个受试者都有自己的运动想象方式和速度，训练空间滤波器时采用相同的时间窗口难以获得最佳的CSP 模式，多时间窗口方法会降低错误选择时间窗口而导致错误分类的风险。在这里将整个时间段分成三个子时间窗，每个时间窗相隔0.5 s。具体的分割做法如下:对于数据集1 采用的三个子时间窗口分别是[0-2.5]、[0.5-3]和[1-3.5]，对于数据集2 使用的三个子时间窗口分别是[3-6]、[3.5-6.5]和[4-7]。

另外，共空间模式提取特征时不携带任何频率信息，然而Kai K A 等人证明选择特定的频带可以提高MI-BCI 的识别率[9]。本文对三个子时间窗分别使用5 阶巴特沃兹滤波器将脑电信号分离成7 个子频带8 Hz～10 Hz、10 Hz～13 Hz、8 Hz～13 Hz(对应于mu 频段)，13 Hz～18 Hz、18 Hz～23 Hz、23 Hz～30 Hz、13 Hz～30 Hz(对应于beta 频段)，并对每个子频带分别应用CSP 提取特征。

1.4 特征提取

共空间模式是MI-BCI 中最常用的特征提取算法之一，该方法本质上是寻找一个投影向量，使得一类数据在向量投影下方差最大，而另一类数据方差最小。CSP 滤波器是通过最大化式(2)实现的:

1.5 特征筛选

经过前面的时间窗口与子频带划分，每个子窗口分成了7 个子频带，每次试验可以得到2p×7 维的特征。由于空间滤波器的有效性取决于识别最佳EEG 频带，现有的算法大都依靠特征选择方法间接筛选子频带，难以将一些无区别能力的频带单元对应的CSP 特征全部丢弃。本文提出在使用LASSO算法前对子频带进行选择，丢弃无区分能力的子频带单元对应的特征。

本文采用能量和CSP 优化函数中特征值λ两个筛选指标对子频带进行筛选[17]。能量指标广泛应用于脑电信号的特征提取中[18]。本文利用所有训练数据，通过式(4)计算每个子频带单元经过CSP 投影后的总能量。

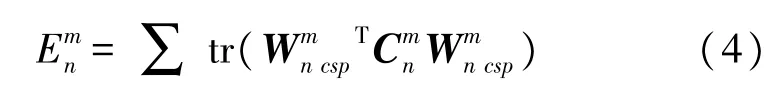
经过频带选择后，还需要对剩余的R＝2p×4 维特征进行稀疏，因为从特征集中选择有效子集，可以最大限度地减少分类误差。LASSO 回归方法是以数据驱动的方式从高维特征中进行特征选择，它不依赖于任何分类器。它通过对模型的系数施加一个L1 惩罚项，在最小二乘估计的基础上使得某些系数趋于0，丢弃系数为0 的特征，进而达到特征选择的目的[19]。LASSO 估计定义为下式(6):

式中，hi与yi分别是第i次试验的R维特征向量和类标签，γ为非负正则化参数，α0和α为回归参数(α0为标量；α是R维向量)。随着γ的增加，α的非零分量的数量减少。本文将均方误差作为稀疏指标，通过5 倍交叉验证选择特征的最佳稀疏度。

1.6 LDA 分类器

线性判别分析在BCI 系统中有着广泛的应用。LDA 的分类思想十分朴素:通过寻找一个投影向量w′，使得同类样本经投影后尽可能接近，异类样本尽可能远离[20]。算法通过最大化以下目标函数求得最优向量w′:

式中，Sb表示类间散度矩阵，Sw表示类内散度矩阵。

2 实验

2.1 数据描述

本文采用BCI 数据集BCI Competition III IVa[21]和BCI Competition IV Dataset I[22]分别对CS-CTFSP有效性进行验证。

数据集1(DS1):第1 个数据集来自BCI Competition III IVa。该数据集记录了5 名受试者(al、aa、av、aw、ay)左手、右手和足部118 个通道的运动想象数据。数据包含了每个受试者280 次试验的时间标记信息，视觉提示持续3.5 s，期间受试者要求执行MI任务。然后，参与者被要求放松1.75 s～2.25 s。EEG原始信号以1 000 Hz 采样，随后在0.05 Hz 至200 Hz之间进行带通滤波，这些信号最后被降采样到100 Hz。单次试验时间轴如图2 所示。

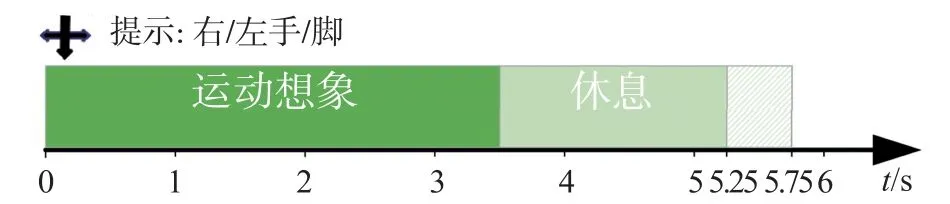
图2 来自BCI 竞赛III 数据集IVa 单次试验

数据集2(DS2):第2 个数据集来自BCI Competition IV Dataset I。此数据集记录了4 名健康受试者(a、b、f、g)的59 通道EEG 数据，每个受试者被要求完成左右手或者双脚的两类运动想象各100 次，每次试验的前6 s 首先会在电脑屏幕中央显示固定的十字，在t＝2 s 时，显示一个指向左、右或下的箭头，参与者被要求执行相应的MI 任务(左手/右手和脚)，然后在6 s～8 s 时屏幕出现黑屏，参与者被要求休息2 s，具体时间轴如图3 所示。原始信号在0.05 Hz 至200 Hz 之间进行带通滤波，后被降采样到100 Hz。

图3 来自BCI Competition IV Dataset I 单次试验

2.2 通道数目配置

通道数量Ms是配置拓展通道集的重要参数，它在分类性能中起着重要的作用。通过5 折交叉验证，根据验证集的平均分类准确率确定参数的最佳阈值。本文以DS1 的受试者aa 为例，得到验证集分类精度随着所选通道数目的变化趋势如图4 所示。

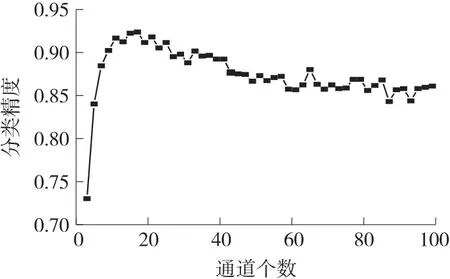
图4 验证集分类准确率随通道个数变化趋势图

在通道数目为3 个(C3、Cz、C4)时验证集只有0.72 的分类精度，随着通道个数的增加，验证集分类精度显著增大，当通道数目为16 个时具有最高的分类准确率0.92，当通道个数继续增加时(超过20个通道)，由于冗余通道和噪声的引入，验证集的分类精度开始降低。因此，本文设置使验证集分类精度达到最大值的通道数目Ms为最佳通道阈值。

3 结果与分析

3.1 分类结果

使用本文提出的方法对DS1 和DS2 两个数据集进行实验，并且和最近提出的运动想象算法BS-CSP[14]，CTFSP[12]，FBCSP[9]，CSP-R-MF[13]等进行比较。在实验中我们采用5×5 折交叉验证方法，将原始EEG 数据集按4 ∶1 随机划分为训练集和测试集，并且重复5 次实验，从而减少实验偶然性对评估结果的影响。5 种分类算法在两个测试集下的分类结果如表2 和表3。

表2 各分类算法在DS1 的准确率比较

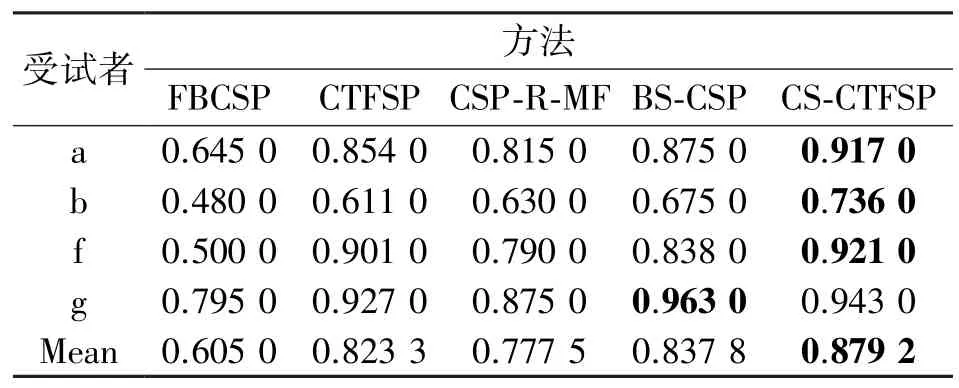
表3 各分类算法在DS2 的准确率比较

针对上述两个公开数据集，从所有受试者的平均准确度上看，本文提出的CS-CTFSP 相对于其他算法表现出了最佳的分类性能。具体来说，对于DS1 数据集的5 位受试者，CS-CTFSP 方法在aa，aw和ay 受试者上获得了最高的分类精度，而BS-CSP方法在al 和av 上获得了最高的分类精度。在DS2数据集上CS-CTFSP 方法在受试者a、b、f 上相较于BS-CSP 分类准确率得到了大幅提高，但在受试者g上低于BS-CSP。

此外，为了验证通道选择算法的合理性，可视化了选择通道分布图，对所选通道采用黑色实心点进行标记。图5 和图6 分别是DS1 受试者aa 和DS2受试者g 的通道标记图。从图中可以看出所选通道分布于额中央和中央顶区的15 个电极，即FC3、FC1、FCZ、FC2、FC4、C3、C1、CZ、C2、C4、CP3、CP1、CPZ、CP2、CP4，而与运动控制相关的神经现象通常分布在这些区域[23]。这在一定程度上验证了方法的有效性。

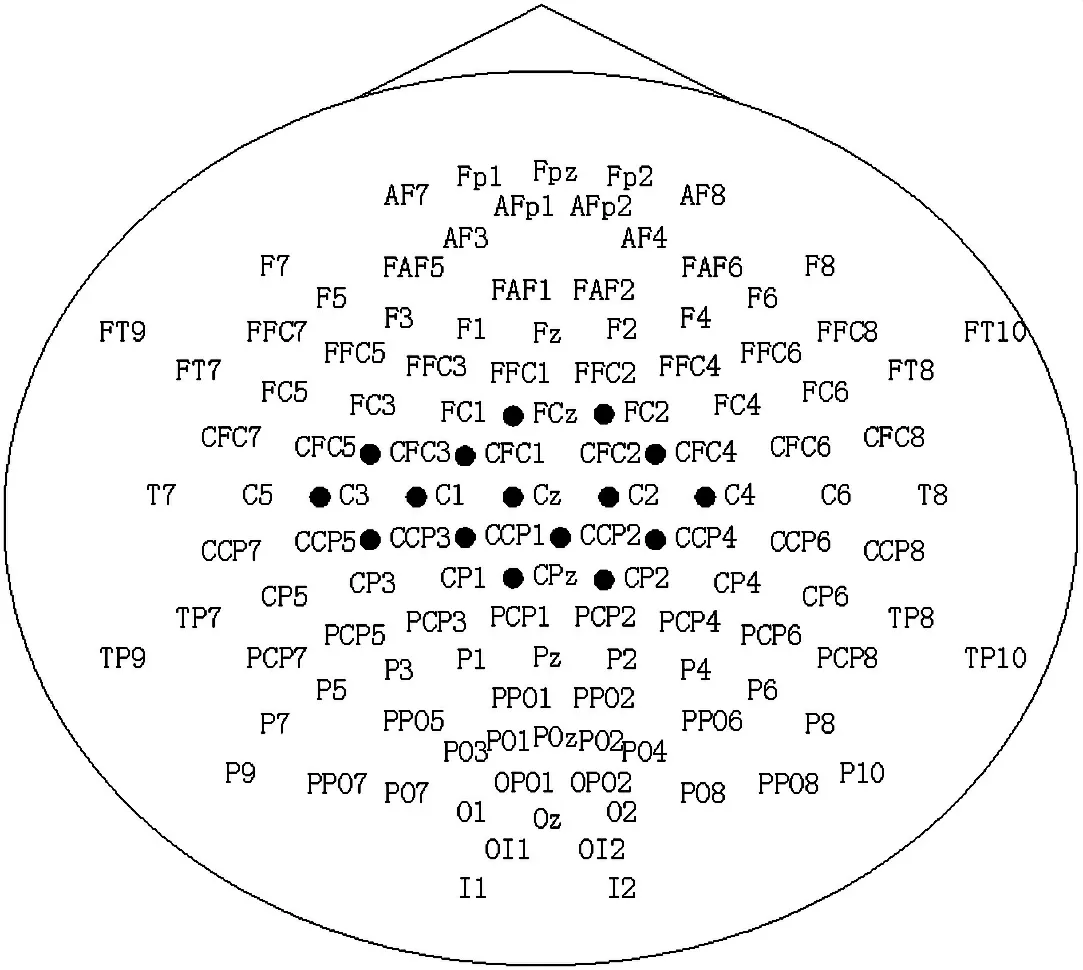
图5 DS1 受试者aa 选择通道分布图

图6 DS2 受试者g 选择通道分布图

3.2 频带筛选前后比较

在DS1 和DS2 数据集上使用全部通道，对比CTFSP 和子频带筛选后CTFSP 的分类准确率，验证子频带筛选算法的效果。

图7 为CTFSP 在子频带筛选前后两数据集下所有受试者的分类准确率。我们发现，采用子频带筛选后的CTFSP 在受试者a、f、g、aa、av、ay 准确率有1%～3%的提升，在受试者b 分类准确率有较大幅度的提升(6%)。

图7 DS1 和DS2 受试者子带筛选前后分类准确率对比

本文在3 个时间窗口上各提取了7 个子频带，一共有21 个频率单元。为了清晰地显示剔除的子频带，我们在受试者av 上可视化每个频带单元，如图8 所示。3 行代表3 个子窗口，7 列代表7 个子频带，每个方块都代表一个频带单元。白色单元表示需要剔除的频带，可以看到受试者av 三个子窗口都剔除了8 Hz～10 Hz 低频单元和23 Hz～30 Hz、13 Hz～30 Hz 高频单元，上述三个频带具有较低的能量和特征值，不具有区分二分类运动想象的能力。文献[14]中av 受试者的通道频带热点图显示，对于受试者av，低于10 Hz 和高于24 Hz 的频带Fisher比都很低，不利于运动想象的分类，这也印证了本文的结论。

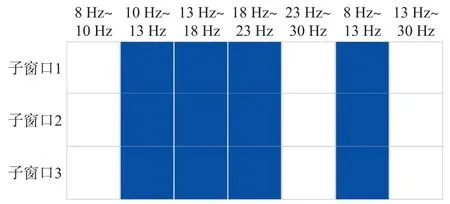
图8 DS1 受试者av 子频带单元剔除示意图

此外，为了更清楚地验证方法的有效性，本文将受试者av 在子频带筛选前后的特征分布可视化，如图9 所示，可以发现后者产生了更容易分离的特征分布，这与两种分类算法的分类结果是一致的。

图9 DS1 受试者av 在子带筛选前后特征分布图

3.3 不同融合策略下的分类性能

由于对整个运动想象时间段进行了多个子时间窗口的划分，并从中提取稀疏特征，因此需要对这些特征进行融合。本文比较了两种不同的融合策略即分类器融合和特征层融合的分类性能。表4 列出了两种不同融合策略下的分类准确率。结果显示分类器融合方法在DS2 数据集上相对于特征层融合具有更高的准确率，在DS1 数据集上两者具有几乎相同的分类性能。

表4 受试者在不同融合策略下的准确率

4 结论

提出了一种基于通道选择的时频共空间模式，能提升运动想象的分类准确率。该方法利用通道间相关性对主通道(C3、Cz、C4)进行拓展，实现通道选择。在所选通道上进行子窗口划分，以应对参与者在MI期间时间延迟的不同。在每个子窗口上对mu 波段、beta 波段及其子波段等提取CSP 特征。之后将共空间模式中的特征值λ 和频带能量作为指标对频带进行筛选，对剩余的特征使用LASSO 算法进行稀疏回归，提取最有用的特征后送入LDA 分类器分类。在两个公开的数据集上对算法进行了验证并与现有算法进行了比较，结果表明所提出的算法具有更高的分类准确率。此外，本文在两个数据集上对比了CTFSP进行子频带筛选前后的准确率，并可视化了最佳分类性能下受试者所选通道的分布情况，从而验证了通道选择和频带筛选算法的有效性。在实际应用中BCI运动想象有多分类的需求，在未来的工作中我们的目标是将算法拓展到多分类场景中。此外，迁移学习能够利用其他受试者的数据(源域)训练待测受试者(目标域)，大大减小了待测试者的训练集，故将迁移学习与CSP 结合也是后续研究的方向。