基于SSAOS-KELM 的指纹库自适应室内定位算法*

孙顺远，徐逸飞，秦宁宁，2*

(1.江南大学轻工过程先进控制教育部重点实验室 物联网工程学院，江苏 无锡 214122；2.南京航空航天大学电磁频谱空间认知动态系统工信部重点实验室，江苏 南京 211106)

近年来，位置服务(Location Based Services，LBS)不断普及，人们对于高精度的室内定位需求也不断增加。不同于传统的卫星定位系统，如GPS、北斗定位系统等，能够在室外实现精确的定位与导航[1]，但室内定位通常面邻诸多问题。由于室内卫星信号衰减，同时还有电磁干扰等，定位精度达不到使用要求，因此如何实现高精度室内定位成为了当前定位导航领域的研究重点[2]。针对室内定位存在的各种问题，国内外的学者提出了很多定位技术，如Wi-Fi、Bluetooth、RFID、UWB 等[3-6]。其中，基于Bluetooth 的定位方法成本较低，可以实现低功耗定位，且大部分智能终端都集成了蓝牙模块，为该技术的推广应用提供了良好的基础。

使用蓝牙技术进行室内定位时，需要预先在定位场景中布置蓝牙信标节点也就是接入点(Access Point，AP)，但这些信标节点只能向外广播信号强度，无法提供到达时间差等信息，因此采用基于接收信号强度(Received Signal Strength，RSS)的指纹法实现定位[7]。为了找出待测点信号与指纹库中各信号之间的关系，许多学者提出了机器学习的方法，如KNN[8]、神经网络[9]等，但是传统的定位方法存在着定位精度低、训练时间长、环境适应性差等缺点。文献[10]提出了基于极限学习机(Extreme Learning Machine，ELM)的室内定位方法，该算法网络结构紧密，无需调整中间权值，极大的减少了训练时间。文献[11]将樽海鞘群优化算法(Slap Swarm Algorithm，SSA)应用到ELM 中，优化了网络中随机产生的输入连接权值和隐藏层的偏置值，提高了ELM 的泛化能力且避免了过拟合的问题。文献[12]在ELM 的基础上引入了核函数，提出了基于核函数极限学习机(Kernel Based Extreme Learning Machine，KELM)的室内定位方法，提高了定位精度同时泛化性能更好。文献[13]则是进一步优化ELM 算法，加入了在线顺序学习阶段。该方法可以逐个或逐组学习新加入的数据，能够快速适应环境的变化，不需要重新学习所有数据，灵活性更强。

综合上述方法的优点，提出了一种基于SSAOSKELM 指纹库自适应的室内定位算法。在定位场景中的各参考点(Reference Point，RP)采集RSS 数据构建指纹库，使用以皮尔森相关系数为距离标准的K-means 聚类算法对定位场景进行分区；然后使用KELM 算法对各个分区建立定位模型，并使用SSA算法优化KELM 中待确定的参数，提高定位精度，提升模型的泛化性能。当环境发生变化，有新数据加入时，先将新数据分配至相应的分区，然后利用在线顺序学习将新增数据集加入定位模型，使用更新后的模型进行定位，使该模型能够跟上环境的变化，提高了自适应性。

1 指纹库构建

1.1 指纹数据采集

在离线阶段，根据蓝牙信标信号强度的衰减模型确定各AP 的安装间距，随后在定位区域中选取若干RP，在RP 采集接收到的各AP 的RSS 和该参考点的实际坐标，并将其存入指纹库中。其中，包括M 个AP，记为APm，m＝1，2，…，M，和N个RP，记为RPn，n＝1，2，…，N，则在RPn处接收到来自APm信号的信号强度可记为rssmn。因此，指纹库可定义为:

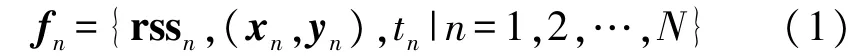
为了减小定位时的数据计算量同时提高定位精度，通常会将定位区域划分为K个更小的目标区域，记为Ck，k∈{1，2，…，K}，则分区指纹库可定义为:

1.2 基于K-means 的指纹数据划分

通常定位指纹库包含了从大量参考点收集到的RSS 数据，而定位测试点只需要使用部分指纹库的参考点数据即可。并且室内环境中存在着噪声，导致异常指纹点的产生，从而使定位产生较大的偏差。因此，采集到指纹数据库后，可以根据各RP 的信号强度以及其所在位置，使用改进的K-Means 聚类算法对指纹库进行划分。将原本的大区域划分成各个小区域，再进行定位。本文使用皮尔森相关系数[14]计算两个点之间的相关性，对于指纹库中的两个参考点fi和fj，相关系数可表示为:

皮尔森相关系数是一种线性相关系数，定义为两点的协方差和标准差乘积的比值。皮尔森系数的值介于-1 到1 之间，值越大，fi和fj之间的相关性就越强。根据各个参考点RSS 的相关性将相似度高的RP 聚为一类，则第k个分区的聚类中心可以用分区中所有RSS 的均值表示:

式中，｜Ck｜表示第k个分区所包含的数据个数。

2 基于SSAOS_KELM 的精确定位方法

2.1 核极限学习机原理

极限学习机(ELM)本质上是一种只有单层前馈网络的神经网络。不同于传统的神经网络，在任意选择输入权值和隐藏层偏差后，ELM 只需求出隐藏层输出矩阵的广义逆矩阵就可以得到输出权值。ELM 以一种新型的学习方式，解决了传统神经网络学习速度慢、易陷入局部最优等缺点。

由1.2 节可知，定位场景已经被分割成了K个小区域。则在区域Ck中，以该区域中参考点的rssn，k作为输入，以各参考点的位置标签tn，k作为输出训练定位模型，其公式如下:

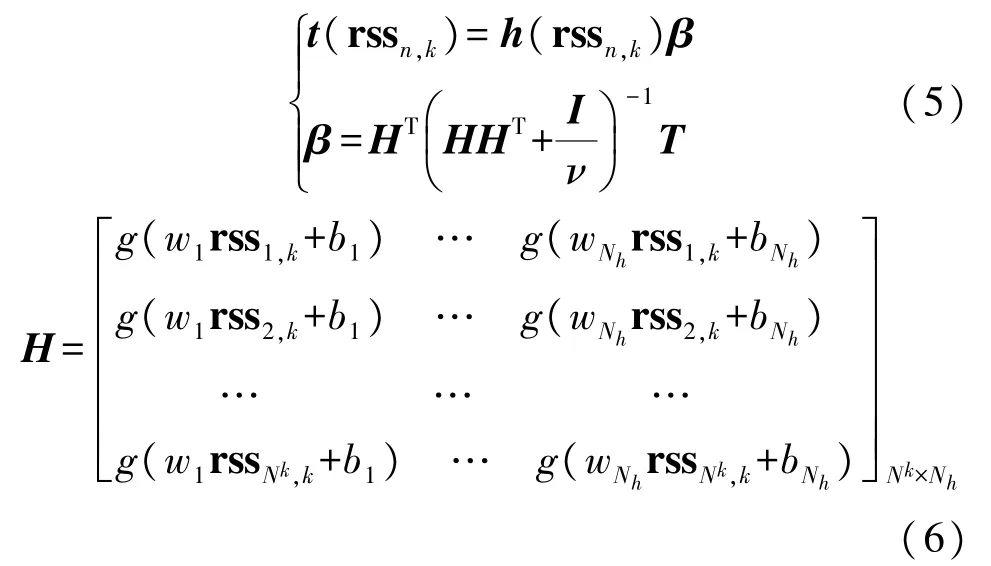
式中，h(x)和H为隐藏层输出矩阵，wi为连接输入层和隐藏层的权值，bi为隐藏层节点的阈值；β为连接隐藏层与输出层的权值；ν为正则化系数；x为输入向量；T为训练集标签，Nh为隐藏层数。

当输出矩阵H未知时，可以使用核函数来代替，映射函数g(x)的具体形式可不用给出。核函数可以将指纹数据升维，把原本在低维空间中并不线性可分的rss 向量映射到高维空间，增大其线性可分的可能性，从而更精准地实现定位。在分区Ck中，KELM 核矩阵可定义为ΩELM＝HHT和Ωij＝h(rssi，k)h(rssj，k)T＝K(rssi，k，rssi，k)，根据式(5)可知，KELM 的输出公式如下所示:

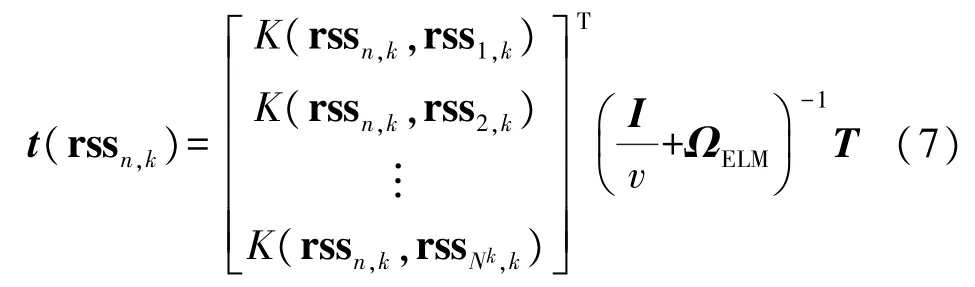
常用的核函数如线性核函数、多项式核函数和径向基核函数(Radial Basis Function，RBF)也称为高斯核函数等都可用于KELM。经过实验，使用RBF 时定位精度最高，其公式如(8)所示:

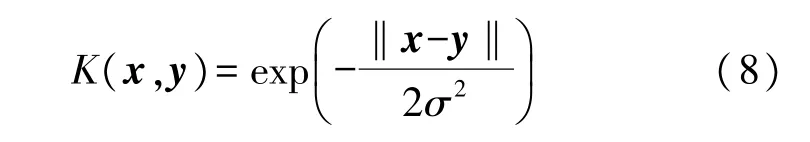
式中，‖x-y‖为样本间欧氏距离的范数，σ为高斯核参数。

KELM 使用核函数矩阵代替了ELM 中的随机映射矩阵，根据式(7)和式(8)可知，只有正则化系数ν和高斯核参数σ会对该分类器产生影响，只需调整这两个参数即可。

2.2 基于樽海鞘优化算法的KELM

2017 年Mirjalili 等人提出了樽海鞘优化算法(SSA)[15]，该算法根据海洋里樽海鞘链的群体觅食行为，进而发展演化而来。樽海鞘链由两种类型的樽海鞘组成:领导者和追随者，领导者处于链的头部，带领群体移动，链上后边的都是追随者角色。

SSA 优化算法主要分为以下2 个部分:

①领导者位置更新

假设樽海鞘群由Q个维度为D的樽海鞘组成，构成了一个D×Q的欧式空间。由2.1 节可知，KELM 只有正则化系数ν和高斯核参数σ需要优化，因此每个樽海鞘个体的维度D即为2。在搜索空间中，每个樽海鞘的空间位置用n＝1，2，…，Q表示，樽海鞘群搜索的食物位置用S＝[s1，s2]T表示。樽海鞘群搜索的上界用ub ＝[vmax，σmax]表示，下界用lb＝[vmin，σmin]表示，规定了参数ν和σ的范围。随后按照式(9)随机初始化种群:

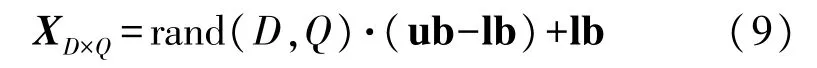
在樽海鞘链移动和觅食的过程中，处于链头部的即为领导者。在种群初始化完成或樽海鞘群位置更新后，SSA 算法以测试集的平均定位误差e为依据，重新确定领导者。e的值越小，则表明该个体离食物越近，将该个体作为领导者，其位置作为新一轮迭代的食物位置。在分区Ck中，平均定位误差e的公式如式(10)所示:

得到食物位置后，用X1表示领导者在搜索空间中的位置，其位置更新公式如式(11)所示:

由式(11)可以发现，领导者位置的更新仅与食物来源有关。式中，控制参数θ2，θ3是均匀分布于0和1 之间的随机数，可以增强X1的随机性，从而提高樽海鞘链全局搜索和个体的多样性。控制参数θ1主要用于控制整个群体的探索能力和开发能力，是SSA中最重要的参数。当θ1的值比较大时，樽海鞘群的探索能力较强，而当值比较小时，则有助于提升局部开发能力。其定义如式(12)所示:

式中，l是当前迭代次数，L是最大迭代次数。

②追随者位置更新

在樽海鞘移动和觅食的过程中，追随者的前后个体是相互影响的，能够有效避免因领导者前期搜索不充分而陷入局部极值的情况发生，并且还能够有效地搜索全局最优。追随者按照式(13)更新其位置:

式中，Xn和Xn-1是彼此紧连的两个樽海鞘的位置，因此所有的追随者都由领导者直接或间接引领。

2.3 在线连续学习

对于许多使用单层前馈网络的应用来说，通常采用的是批量学习的方法。当定位场景发生变化时，需要将新数据和旧数据一起重新训练，从而消耗了大量的时间。而在线顺序极限学习机(Online Sequential Extreme Learning Machine，OS-ELM)克服了此缺点，该方法能够对隐藏层输出权值矩阵进行分解，不需要重新训练定位模型，因此能够更好地适应环境变化。OS-ELM 不仅可以逐个学习训练数据，还可以逐块学习训练数据，并且可以丢弃之前已经训练好的数据，是一种通用的顺序学习算法。

使用KELM 替代ELM 后，为简单起见，令A＝(I/v＋ΩELM)。没有新数据加入时，在分区Ck中，记A矩阵为At，k，其公式如式(14)所示:

在输入一组新测得的指纹数据fadd，n＝{rssadd，n，(xadd，n，yadd，n)｜n＝1，2，…，h}后，通过计算新增数据的rssadd，n与各聚类中心之间的皮尔森相关系数，将该数据分配至已划分好的相应区域，判断依据如下:

在各分区收到新增数据后，记A矩阵为At＋1，k，公式如式(16)所示:

式中，Ut，k和Dt，k的公式如下:

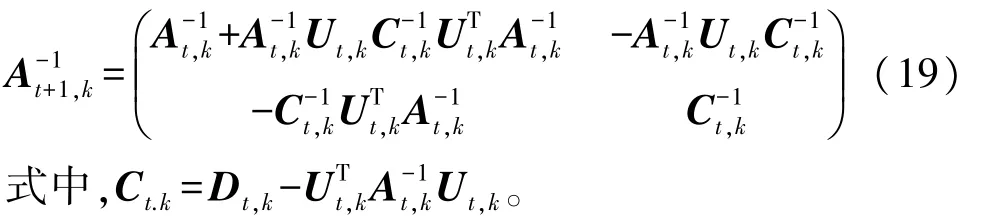
在线阶段，初始化定位模型训练完成后加入几组新数据，数据的总数量为π，经过训练后得到Aπ。随后，在实际场景中采集Nt组数据，记为ftest，n＝{rsstest，n，(xtest，n，ytest，n)，ttest，n｜n＝1，2，…，Nt}。按照式(15)将测试数据分配至相应分区作为该分区定位模型的输入，可得:

2.4 算法计算复杂度分析

在OS-KELM 算法中，At＋1是在At的基础上得出的。因此，在线顺序学习的过程中，At需要一直保存而不能像OS-ELM 一样用完即弃。该方法都能将新采集的数据加入定位模型中，不需要重新训练，大幅减轻了计算量，提高了模型的自适应性。At＋1的计算成本的公式如下:

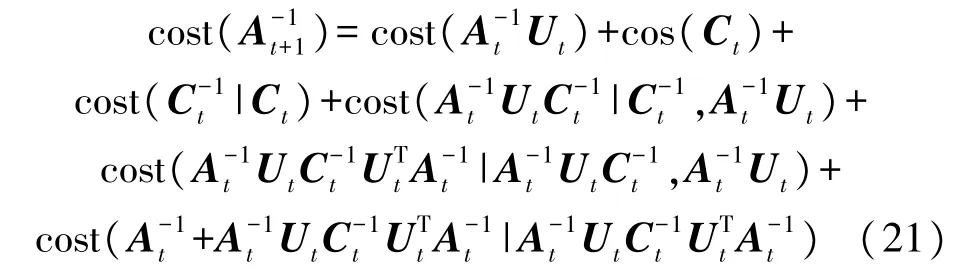
式中，cost () 表示括号内变量的计算成本，cost(*｜*)表示括号内后一个变量已知的情况下，前一个变量的计算成本。其中，矩阵的维度为N×N，矩阵Ut的维度为N×h，矩阵Ct的维度为h×h，则At＋1的计算成本为:

2.5 算法流程

基于SSAOS-KELM 的指纹定位算法流程如表1所示。

表1 SSAOS-KELM 算法流程

3 实验分析

3.1 实验配置

实验场景为江南大学物联网工程学院C 区一楼“L”型走廊区域。本实验研究的是基于蓝牙的室内定位技术，采用NRF52832 低功耗蓝牙模块作为信标节点。根据测试所得的蓝牙信号强度衰减趋势，在走廊的边沿每隔一定距离布置一个蓝牙信标作为AP。场景细节描述如下:

“L”型走廊区域由两个连通的矩形区域组成，区域中共放置了11 个AP，如图1 所示。以1 m×1 m为单位进行划分，在场景中共得到156 个点并将其作为采样点，即为RP。在每个RP 采集四次RSS 数据，与各RP 的实际位置和标签一起组成定位指纹数据库。将其中468 组数据作为训练集，156组数据用于测试和验证，用于训练的468 组数据中再分出156 组数据作为新增数据集。

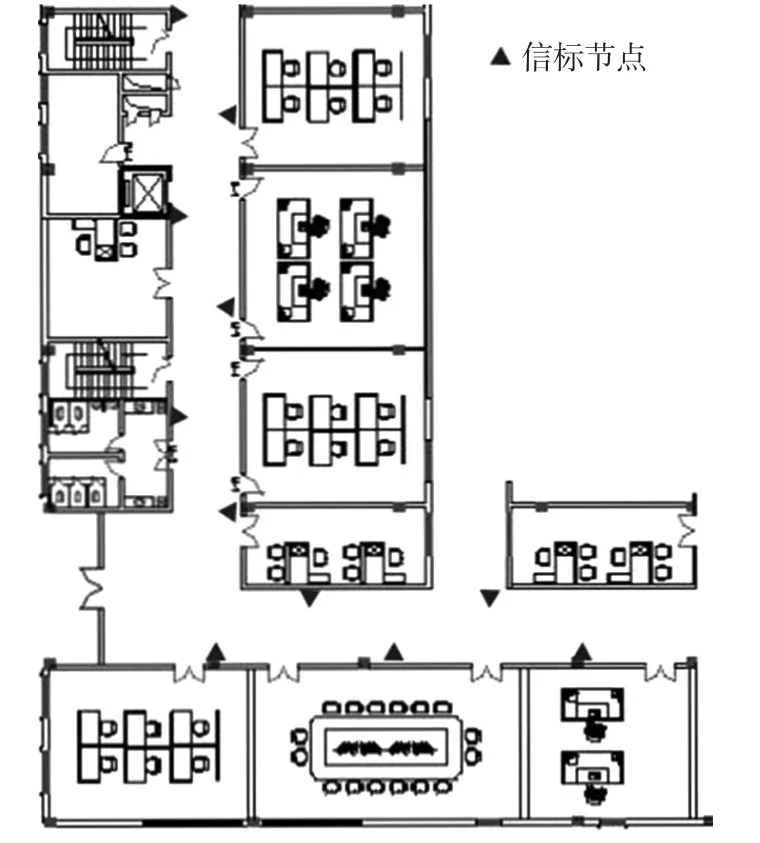
图1 实验场景平面图

在仿真阶段，采用MATLAB2019b 仿真平台，选取ELM、BP 神经网络作为对比算法与本文提出的算法进行对比分析。算法中SSA 优化部分参数配置为:种群数量Q＝30，最大迭代次数L＝30，正则化系数ν的搜索范围为[0，200]，高斯核参数σ的搜索范围为[0，100]。对比分析聚类前后效果、新增数据加入前后效果以及各算法的定位精度。

3.2 聚类效果分析

本文采用了基于皮尔森相关系数的K-means 聚类方法对指纹库中的RP 进行划分，将相关度高的RP 归为一类。在“L”型走廊区域中，某个AP 周围的信号强度分布如图2 所示。不难看出，靠得越近则信号强度越大，总体呈高斯分布。因此，可以根据各RP 的信号强度对该区域进行聚类，聚类效果如图3 所示。

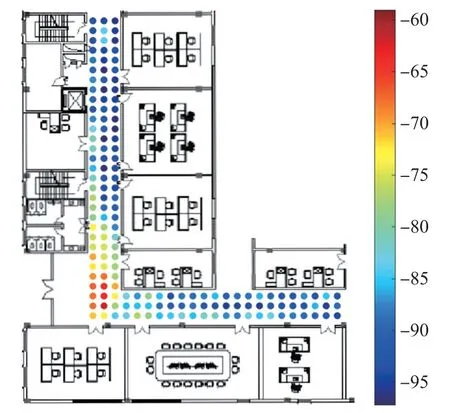
图2 实验场景中某AP 信号分布

图3 聚类效果图

将“L”形走廊场景中的156 组测试数据采用本文所提出的算法进行测试，在聚类前和聚类后各做一组实验，通过累计误差分布图(Cumulative Distribution Function，CDF)展示定位误差，如图4 所示。由图可知在聚类前，仅有60%的测试点定位误差小于2 m，而聚类后90%左右的测试点定位误差小于2 m，定位精度明显提高。同时，定位误差的最大值也从6.2 m 下降至3.5 m，稳定性也得到了明显提升。故采用皮尔森相关系数改进的K-Means 算法能有效提升定位的精度与稳定性，对抗环境干扰。

图4 SSA-OSKELM 聚类前后误差分析

3.3 在线顺序学习对自适应性的影响

3.3.1 定位精度分析

在实际应用中，可能存在指纹库数据收集不全面、环境发生改变等情况。当新数据加入时，传统的定位方法通常需要重新训练模型。本文提出了使用在线顺序学习新加入数据，避免模型的重新训练，在某种程度上可以减少离线阶段的人力和时间成本，提高算法对环境的自适应性。

在“L”形走廊场景中，将新增数据集分两次加入。由表2 可知，除了分区三由于第一次更新时，新增数据集存在异常数据，导致定位误差增大外，其他分区定位误差都会随着新增数据加入而变小。两次模型更新后，在新增加了1/3 数据的情况下，总体平均误差也由1.26 m 降至1.06 m，定位精度提升了15%。因此，当环境发生变化时，本文所提出的算法能够在原有定位模型的基础上更新模型，自适应性更好。

表2 在线学习前后的平均定位误差 单位:m

3.3.2 时间复杂度分析

当新增数据加入时，使用在线顺序学习和模型重新训练所需的时间如表3 所示。

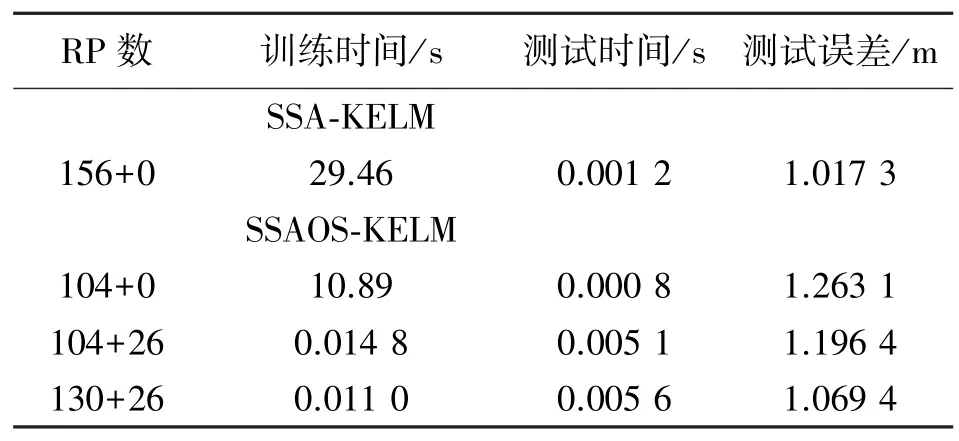
表3 SSAOS-KELM 与SSA-KELM 比较

从表中可以看出，在原有数据库基础上新增了两组数据后，对156 个参考点的数据整体进行训练将耗费近30 s 的时间，而使用在线顺序学习加入两组数据在1 s 以内就可以完成。因此当目标区域越大时，重新训练模型耗费的时间越多，本文所提出的方法避免了重新训练，可以大大减少训练时间。

3.4 定位误差分析

定位误差主要选取误差箱型图和累计误差分布(CDF)来进行分析，在“L”形走廊场景中分别使用ELM、BP 神经网络和SSAOS-KELM 算法进行测试，实验结果如图5 和图6 所示。

由图5 可知，本文提出的SSAOS-KELM 算法与其他两种算法相比，有着最低的误差中位线，约为0.63 m 左右，定位精度最高；BP 神经网络与该算法误差中位线相近，但其误差分布较广，离群点多，稳定性稍差。所有的算法经过聚类后，离群点变少，定位精度均有所上升。

图5 三种方法的定位误差箱型图

由图6 可知，本文提出的算法近90%的测试点定位误差在2 m 以内，最大定位误差也是最小的；BP 神经网络次之，但其聚类前后误差相差不大，最大定位误差稍有减小；ELM 算法定位误差最大。在聚类后，这三种算法的累计误差均有不同程度的提升。总体而言，本文所提出的算法相较于其他两种算法定位精度和稳定性更好。

图6 三种方法的累计定位误差分布图

4 结论

基于SSAOS-KELM 指纹库自适应的室内定位算法，利用皮尔森相关系数改进的K-means 算法对待定位区域进行聚类划分；随后通过樽海鞘(SSA)算法优化KELM 参数为每个分区建立定位模型；最后通过在线顺序学习添加新数据，更新定位模型，并实现定位。从实验结果可以看出，算法的定位精度明显提高，且对环境的适应性更好。但该算法只能在定位模型中加入新数据，并不能将模型中已经发生改变的旧数据清除，有待改进。