不确定非完整AGV的滑模路径跟随控制
2022-02-04陈天炎
陈 天 炎
(福建船政交通职业学院, 福州 350007)
0 前 言
随着机器人技术的日益成熟,移动机器人在居家服务、空间探索、智能制造、现代军事等领域得到了广泛的应用[1]。自动导向车(automatic guided vehicle, AGV)是一类重要的移动机器人,主要用于现代物流系统的物料输送。AGV根据预先规划的路径进行导引运动,到达指定工作点后实施作业任务,导引控制效果直接影响AGV的作业效率和作业质量。AGV一般为轮式驱动,其导引控制主要包括切换控制、轨迹跟踪和路径跟随等[2-4]。其中,切换控制是指根据AGV在路径中的不同位置进行多模式切换,该方法控制精度低,且要求AGV起始点必须在路径附近。轨迹跟踪的控制精度较高,但轨迹表征较为复杂,且轨迹跟踪控制的运行速度为系统控制输入,当跟踪复杂轨迹时,不利于AGV在应用系统中的调度控制。路径跟随是指通过调整AGV的姿态角,使其与路径跟随点切向角保持一致,该方法有助于运行路程的统计。
AGV工作环境复杂,容易受到外界扰动的影响,同时其自身结构参数也无法精确获得,现有的路径跟随方法大多未考虑不确定因素对AGV控制精度和适用范围的影响。本次研究建立了包含不确定因素的AGV路径跟随误差控制模型,基于Lyapunov法设计全局滑模控制器,以保证控制的精度,提高系统的鲁棒性。
1 运动学模型分析
研究对象为两轮差速驱动型AGV,其运动形式主要通过调整2个独立驱动轮的速度和转向来实现,并配置若干全向轮,以提高AGV的承载能力。
AGV的本体结构和运动空间坐标系如图1所示。其中,xIoIyI为全局坐标系{I},xFoFyF为局部坐标系{F},oF为AGV在参考路径上的跟随点,oFyF为oF点沿参考路径方向上的切线,θr为oFyF与xI轴的夹角,Q为AGV的质心,θ为AGV的导向角度,v和w分别为AGV的前进速度和转动速度。p、q分别为oF点和Q点在全局坐标下的直线向量。
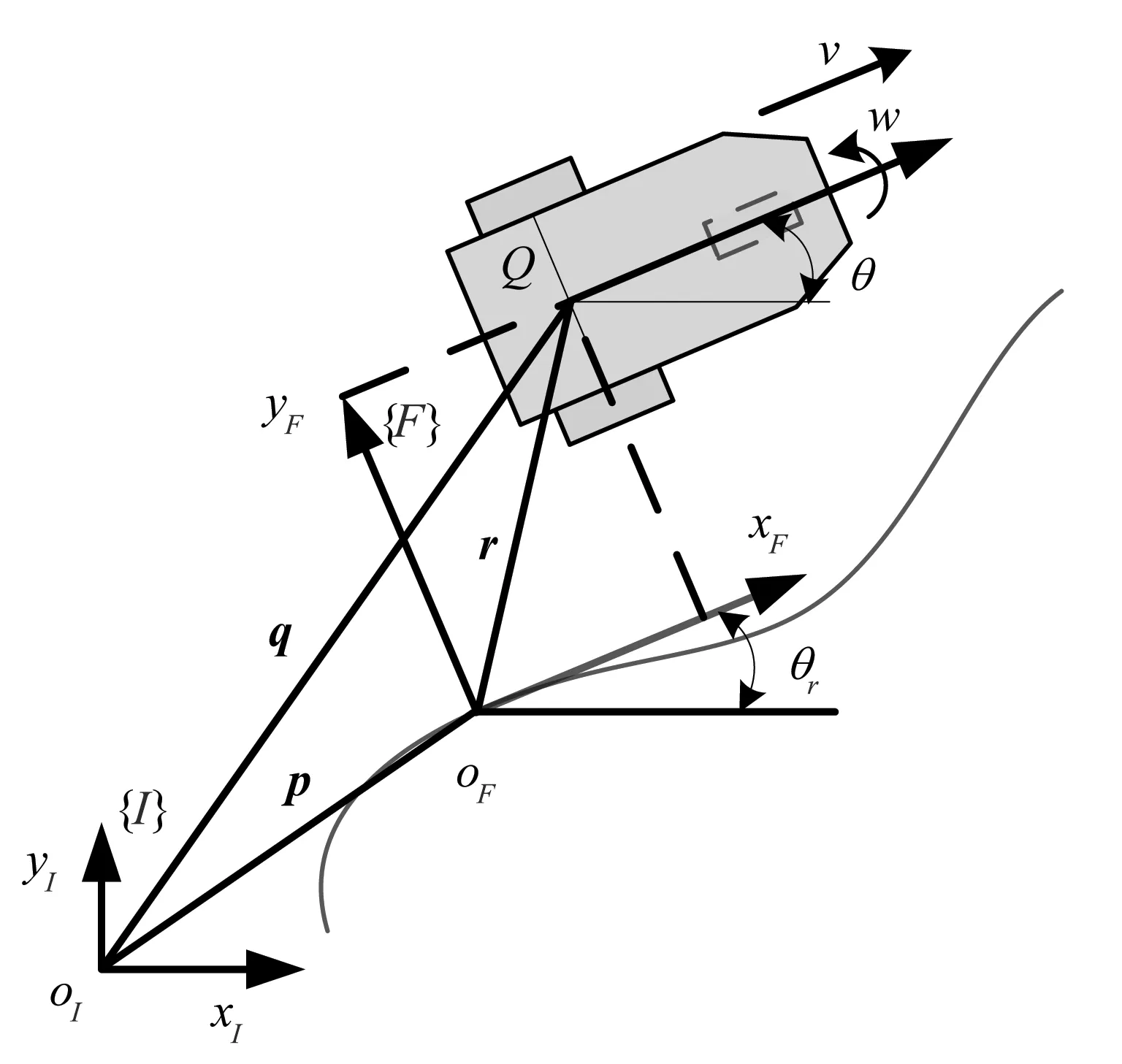
图1 AGV的本体结构和运动空间坐标系
定义AGV在全局坐标系下的位姿为ξ=[xyθ]T,两轮差速驱动型AGV的运动学模型如式(1)所示[5]:

(1)
定义ϑ为oF点沿路径方向的行程,c(ϑ)为路径曲率,则向量r沿oF点的转动速度wc如式(2)所示:
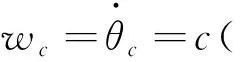
(2)
定义[xF,yF]为Q点在xFoFyF坐标系下的坐标,则有式(3):
(3)
在坐标系{F}下,Q点的速度满足式(4):
(4)
将坐标转换为矩阵:
将式(1)、式(3)代入式(4),同时考虑系统不确定因素对模型的影响,可建立AGV在Serret-Frenet框架下的全局路径跟随运动学模型[6],如式(5)所示:
(5)

由式(5)可知,AGV为多输入多输出耦合的复杂系统,在实现精确路径跟随的同时,AGV还要能够抵御系统的不确定项对其结果产生的影响,控制器的设计难度较大。
2 控制器设计
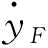
定义期望角度δ,如式(6)所示:
(6)
式中:θd为任意给定参考角度值θd∈(0,π/2);kδ为正常数。
采用Lyapunov直接法对控制器进行设计,定义滑模面为:
s=k1(θe-δ)
(7)
式中:k1为正常数。
对式(6)进行求导,整理可得:
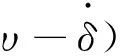
(8)
设计正定Lyapunov函数为:
(9)
式中:λ1为正常数。

=xF[-(1-cyF)υ+vcosθe+η1]+
=xF(vcosθe-υ)+xFη1+yFη2+yFvsinδ+
=xF(vcosθe-υ)+yFvsinδ+
(10)
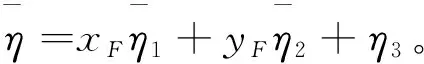
设计指数趋近律的滑模控制器为:
(11)
式中:k2、u1、u2为正常数。
定理1:对于AGV路径跟随运动学模型(5),控制器(11)可使闭环系统渐进稳定。
证明:采用函数Lyapunov,将式(11)代入式(10)可得到:
(12)
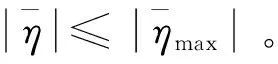
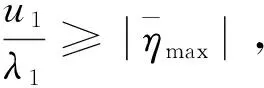

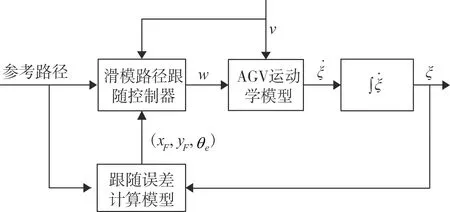
图2 AGV路径跟随控制器结构图
3 仿真实验
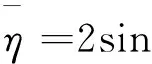

图3 常规控制器跟随轨迹对比
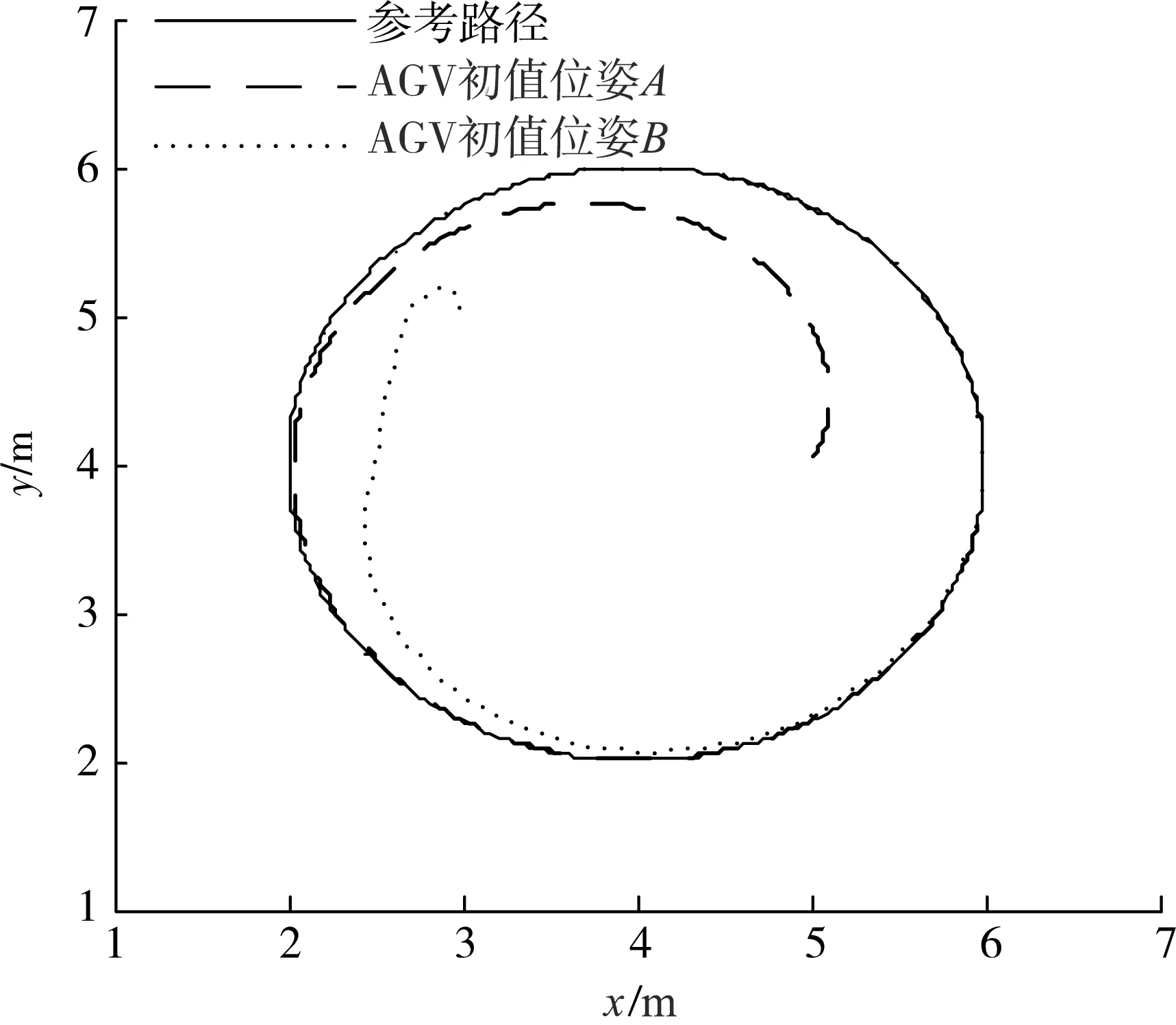
图4 AGV控制器跟随轨迹对比
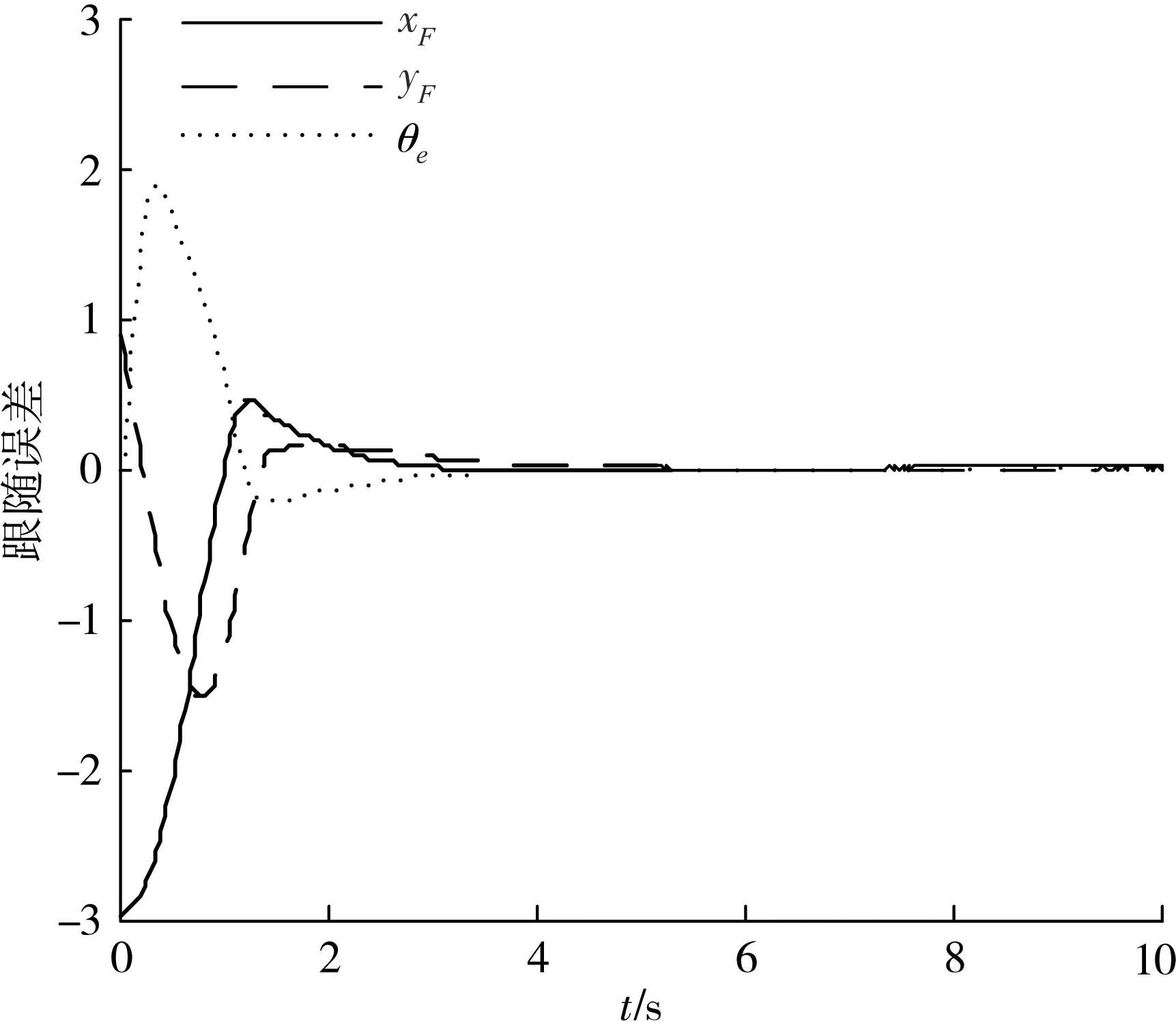
图5 AGV控制器的跟随误差(A起始点)

图6 AGV控制器的控制输入变化(A起始点)
4 结 语
精确跟随给定路径是AGV进行物料运输作业的基础,由于其工作环境复杂,加上其自身结构参数无法精确获得,AGV不可避免地受到模型不确定项和外界干扰的影响。本次研究建立了AGV的不确定路径跟随模型,设计了一种基于指数趋近律的滑模路径跟随控制器,以消除系统不确定项的影响,并减小了滑模抖振。仿真实验表明,该控制器系统运行平稳,控制精度较高,实用性较高。
