Fermat型方程亚纯解的一点注记

杨振柳，吕 锋

(中国石油大学(华东)理学院，山东 青岛 266580)

1 引言及主要结果

在2021年，陈敏风、高宗升和黄志波[15]证明了如下定理。

定理A考虑如下差分方程

fm(z)+fn(z+c)=eαz+β

其中m、n≥1,α、c∈C{0},β∈C为复数。

则当n=m≥3或者(n,m)=(2,3)、(2,4)、(3,2)、(4,2)时，方程没有非平凡的有限级亚纯函数解。

根据上述结论，我们提出下列问题。

问题1注意到αz+β是一个一次多项式，上述结论能否推广到一般的多项式?

问题2上述结果能否由有限级推广为超级小于1的情况?

本文中,我们利用Nevanlinna值分布理论、差分模拟结果以及椭圆函数的性质研究了上述问题，得到了下面结论。

定理1方程f(z)2+f(z+c)3=eP不存在超级小于1的非常数亚纯解，其中c≠0为一常数，P为多项式。

定理2方程f(z)2+f(z+c)4=eP不存在超级小于1的非常数亚纯解，其中c≠0为一常数，P为多项式。

注显然，根据以前的结论，当m≥4,n≥3时，方程fm(z)+fn(z+c)=eP的亚纯解的问题易解决，其余情况留待后续研究。

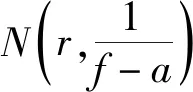
2 引理

引理2.1[6,15,17]在复平面C上，函数方程fn(z)+gm(z)=1的非常数亚纯函数解有以下结论：

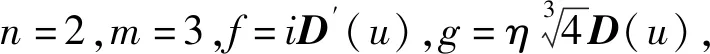
(2)当n=2,m=4,f(z)=sn′(u),g(z)=sn(u)，其中u为非常数整函数，sn为Jacobi椭圆函数满足sn′2=1-sn4。

引理2.2[18]设T:[0,+∞)→[0,+∞)是正值、非减的连续函数，令s∈(0,∞)。若T的超级严格小于1，即

令δ∈(0,1-ζ)，则

这里r→∞去掉一个对数测度有限的集合。

下面，我们运用类似文献[13]中的方法，证明定理1和2。

3 定理的证明

定理1的证明假设f为方程的一个非常数亚纯解，下证矛盾。我们将方程改为

进一步可得

(3.1)

上述等式变形得

(3.2)

由D′2=4D3-1，可得

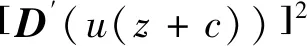
这里A是一个非零常数。进一步由引理2.2可得

3T(r,D(u(z+c)))=

T(r,4D3(z+c)-1)+O(1)=

O(rdegP)

上式表明了

T(r,D(u(z+c)))≤

故D(u(z+c))为有限级，进而u是一个多项式。再由(3.1)得

N(r,D(u(z)))=N(r,D′(u(z+c)))=

另外，通过引理2.2可得

N(r,D(u(z)))=N(r,D(u(z+c)))+

比较上面两式，可得

(3.3)

注意到D的极点重数为2和u是一个多项式。故

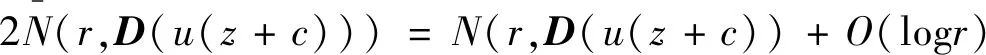
其与(3.3)式矛盾，故定理得证。

定理2的证明我们用类似定理1的方法证明定理2。同样，假设f为方程一个非常数亚纯解,下证矛盾。我们将方程改为

进一步可得

(3.4)

上述等式变形得

(3.5)

由sn′2=sn4-1，可得

[sn′(u(z))]2=1-sn4(u(z))=

进一步由引理2.2可得

4T(r,sn(u(z)))=T(r,1-sn4(u(z)))+O(1)=

上式表明了

故sn(u(z))为有限级，进而u是一个多项式。再由(3.4)得

N(r,sn(u(z+c)))=N(r,sn′(u(z)))=

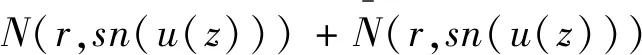
另外，由引理2.2,可得

N(r,sn(u(z+c)))=N(r,sn(u(z)))+

根据上面两个式子，可得

(3.6)

注意到函数sn的极点重数为1和u是一个多项式。故有

N(r,sn(u(z+c))+O(logr)

其与(3.6)式矛盾，故定理得证。