基于CT扫描的不同粒形滤料孔隙结构特征

蔡九茂，宋 蕾，张文正，翟国亮，许 强，李鹏来

基于CT扫描的不同粒形滤料孔隙结构特征

蔡九茂1，宋 蕾1，张文正1，翟国亮1※，许 强2，李鹏来3

（1. 中国农业科学院农田灌溉研究所/农业农村部节水灌溉工程重点实验室，新乡 453002； 2. 安徽菲利特过滤系统股份有限公司，马鞍山 243071；3. 内蒙古龙泽节水灌溉科技有限公司，赤峰 024005）

滤层孔隙结构直接影响过滤过程中的颗粒沉积和运移效果。为了掌握砂石过滤器不同粒形滤料组成滤层的内部孔隙结构特征，该研究以粒径为1～1.18 mm的普通石英砂（QS1）、天然海砂（SS2）、改性玻璃（MG3）和玻璃微珠（GB4）4 种滤料为研究对象，采用CT 扫描技术对滤层孔隙模型进行了三维重构，利用VGStudio MAX、Image J等计算机图像处理软件，分析了 4 种滤层的孔隙率、孔径大小及孔隙形状参数，并结合分形理论确定了 4 种滤层孔隙结构的计盒分形维数。结果表明：4种滤层的表观孔隙率范围分别为39.7%～44.6%、38.5～42.3%、40.7%～45.6%、34.8%～38.7%，对应体积孔隙率分别为0.422、0.412、0.441、0.366；对应孔径范围分别为75～960、80～760、70～1 050、85～930m，圆度值区间分别为1.59～1.78、1.35～1.54、1.65～2.03、1.20～1.36，扁平度值区间分别为2.62～2.75、2.05～2.20、3.04～3.21、1.94～2.04，计盒维数均值分别为1.621、1.566、1.661、1.446。该研究定量表征了滤层孔隙结构特性，得出不同粒形滤料细观孔隙结构的差异：滤层表观孔隙率呈现“上高下低”分布规律，孔径分布规律表明滤层内均是小孔隙占多数，大孔隙占少数，且孔隙以狭长型为主。随着滤料棱角度增加，表观孔隙率分布越分散，体积孔隙率越大，大孔隙占比也相应增加，最大达到17.24%（MG3），孔隙形状更加偏离球形，表征孔隙结构复杂性的计盒维数相应增加，且分形维数与孔隙率呈负相关关系。滤层孔隙结构研究可为后续研究滤层内颗粒沉积和运移规律奠定基础。

微灌；CT图像；图像处理；孔隙结构；孔隙率；分形维数

0 引 言

微灌技术是缓解农业水资源短缺、提高水资源利用效率和生产效率的重要措施，近年来在中国多地得到了快速应用与推广[1]。首部过滤系统是保证微灌系统正常运行的关键设备之一。其中，砂石过滤器因为其独特的过滤运行机理，在世界范围内被广泛采用[2]。评估微灌砂石过滤器性能优劣的指标主要是过滤效果及反冲洗特性[3]。滤层配置模式，包括滤料类型、滤料粒径、滤料形状、滤层厚度、过滤速度等参数，直接影响过滤和反冲洗效果[4]。

近年来，国内外多位学者对砂石过滤器滤层配置参数对过滤反冲洗效果影响规律进行了相关研究。Haman等[5]认为过滤系统应该能够处理滴灌流道1/10和微喷头孔径1/5以上的颗粒，砂石过滤器适宜的砂滤料粒径近似等于两倍的流道尺寸；Goyal[6]总结分析了滤料粒径与过滤精度之间的对应关系；Mesquita等[7]采用分层取样的方法，分析了不同粒径滤料的分层去除效率变化规律；Kandra等[8]开展的雨水回用过滤试验结果表明，雨水中泥沙粒径e及其与滤料粒径e的比值e/e是滤层配置的关键参数。关于滤料粒径和滤层厚度的关系，Mcgivney等[9]提出以/值为依据进行滤层配置，而张宇[10]通过对比不同粒径和滤层厚度试验数据，分析了/和/2两个关系式与过滤指标（浊度、水损）之间的相关关系，认为/2能更好地描述预测过滤特性变化；张建锋等[11]则认为滤后水颗粒截留效果主要取决于滤层厚度，与滤层厚径比/值没有相关性，并认为9 m/h以下的滤速对于砂滤层截留特征没有显著影响，这一结论与张文正等[12]试验结论相符。以上研究主要是针对粒径和滤层厚度对过滤效果的影响规律，研究成果较为系统全面。近年来国内外新型滤料不断出现，各种改性滤料除了粒径分为不同级别，粒形也多种多样，球形度和粗糙度指标差异较大。Soyer等[13]认为改性玻璃滤料可以有效降低滤层水损，提高悬浮固体和藻类的去除率；Kandra等[14]评价了滤料粒形和滤速对颗粒堵塞过程的影响，认为粒形对堵塞过程发展和固定颗粒去除率影响较大；Bové等[15]测定了玻璃和石英砂滤层孔隙率、球形度、实密度和体积密度等参数，并建立了不同粒形滤料滤层的清洁压降预测模型。粒形参数直接影响滤层的孔隙结构特征，从而影响滤层内颗粒沉积和运移规律。国内外关于多孔介质内微小颗粒沉积和运移的研究较多，但主要是在雨水过滤回用、地下水回灌、污染物扩散、反滤层设计、注浆加固等领域，众多学者将试验和理论相结合，从颗粒粒度、渗流速度、孔隙结构、颗粒形状等方面研究了颗粒在多孔介质滤层内的迁移特性，系统研究了各单因素对颗粒运移沉积影响机制[16-19]。在微灌砂石过滤领域，要研究杂质在滤层内的运移和分布规律，首先要掌握微细观的滤层孔隙结构特征，由于滤层内部孔隙分布复杂且随机性强，利用常规手段无法直观观测和定量描述。因此，目前为止关于微灌砂石过滤器滤层细观孔隙结构的研究几乎没有。

基于CT扫描的无损检测技术在土壤结构[20-22]、岩土工程[23-25]等多孔介质研究领域已经得到了广泛应用，为砂石滤层孔隙结构研究提供了研究手段和方法借鉴。因此，本文将CT扫描技术、图像处理技术和多孔介质分形理论相结合，针对4种不同粒形滤层的细观孔隙结构特征进行了深入研究，重点量化分析了滤层孔隙率分布、孔径大小、孔隙形状等参数，并计算了表征孔隙结构复杂度的计盒分形维数，对不同粒形滤料组成的滤层内部孔隙结构特征的定量表征，以期为后续研究颗粒沉积和运移奠定了基础。

1 材料与方法

1.1 试验设备与测试样品

CT扫描试验在洛阳中信成像智能科技有限公司重点实验室完成。工业CT扫描仪型号为CI6M320I，主要参数：峰值电压160 kV，电流240 mA，扫描时间1 s，扫描最低分辨率为0.15 mm。扫描器配备最大视野为2 048×2 048像素、32位的X射线探测器，CT 扫描系统组成如图1所示。

图1 CT扫描系统

测试样品为 4 种滤料，包括普通石英砂QS1、天然海砂SS2、ASM改性玻璃MG3和玻璃微珠GB4，滤料颗粒粒径范围为1.00～1.18 mm，均从市场上直接采购并多次筛分后取样使用。将测试样品放入有机玻璃柱作为扫描样品，有机玻璃柱的柱体高 150 mm，直径 80 mm，壁厚5 mm，样品厚度为100 mm。根据 CT 扫描仪的精度，本试验中能辨别的最小体素值为0.065 mm。

1.2 滤层重构与二值化图像获取

CT扫描时，载物台360°旋转，每旋转1°，系统自动采集5张照片，每份滤料共采集1 800张切片图像，扫描结束后，扫描原始图片采用FDK算法进行反投影重构，通过专业的CT数据分析和可视化处理软件VG Studio MAX，可进行模型展示和后处理，如图2所示。通过选择不同的切片位置，可获得各方向上的滤层灰度图像切片。为排除滤料与容器接触区域的干扰，选择各滤层中心圆形区域作为感兴趣区域（Region Of Interest，ROI）进行局部分析，横截面CT切片灰度图和提取的ROI区域如图3所示。

图2 重构后的4种滤层三维视图

要想分析滤层孔隙结构特性，首先要对CT扫描切片进行二值化处理，采用黑白两色来表征孔隙和滤料区域[26]。借助ArcGIS软件对原始CT图像进行数字图像预处理及阈值分割。首先将ROI周边的背景裁剪去除，用中值滤波对图像进行降噪处理；然后观察CT图像的灰度直方图，由于本次扫描的滤层内部仅有孔隙和滤料两种物质，且二者密度差异显著，因此灰度值边界也较为明显，因此采用人工手动进行阈值分割，选取原则是在灰度直方图波谷位置多次试验不同的阈值，反复对照分割后的图像是否准确勾勒出了颗粒与孔隙的边界，最后确定出阈值[27]。图4为滤料SS2和GB4采用不同分割阈值获得的二值化图，可以看出阈值选择直接影响孔隙占比和孔隙形状。

图3 滤层横截面切片及局部感兴趣区域（ROI）

图4 SS2和GB4不同分割阈值下的二值化图

1.3 图像处理获取滤层孔隙特征

1.3.1 表观孔隙率及体积孔隙率计算

统计分析二值化处理后的图像上白色孔隙部分像素点占图像总像素点的比例，即可得到二维切片图像的表观孔隙率。对一系列二值化CT图像处理后获得的表观孔隙率统计分析，可以确定表观孔隙率沿着不同深度方向的分布规律，进而可根据以下步骤计算整个试样的体积孔隙率[25]。首先从重构的3D模型中抽取三维表征单元体（Representative Element Volume，REV），如图5所示。

注：z1、z2代表选取单元体z方向的边界；o为坐标原点，xyz分别为3个坐标轴方向；dz代表相邻两层切片之间的距离。

设相邻两层CT切片之间的距离为d，选取的计算单元体的尺寸边界为1，2，n()为位置处横切片的表观孔隙率，假设所处高度为从下到上的第个d区间内，因此，当d尺度足够小时，高度位置紧邻的两个切片间的体积孔隙率可以表示为：

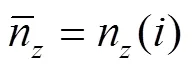
因此，该选定的计算单元体的三维体积孔隙率可用所有离散切片的表观孔隙率近似表示为：

式中为1～2高度区间内的d的数量。

由此通过截取的单元体切面的表观孔隙率，计算得到整个试样的体积孔隙率。

1.3.2 基于VG Studio获取滤层孔隙结构分布规律

采用VG Studio软件的孔隙及夹杂物分析模块，可以将ROI范围内的所有孔隙进行特征提取，包括孔隙直径、体积、表面积、紧密度、球度、投影面积、平均灰度等指标。由此，可以准确地对孔隙的数量、大小等分布特征进行统计分析。

1.3.3 基于Image J获取孔隙形状特征

孔隙形状是影响多孔介质材料渗透性和杂质运移的关键因素。表征孔隙形状的参数主要有圆度、扁平度等。从4种滤料扫描结果中，按照从低到高的顺序，选取5个不同位置，每个位置附近选择3张切片图像，采用专业的开源图像处理软件Image J，对二值化后的CT切片图像进行矢量化处理，可以分析微孔隙的体积分数、粒径分布以及圆度等参数。

圆度计算公式如下：

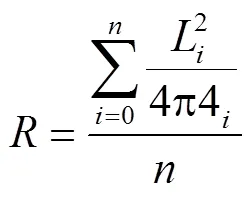
式中为滤层孔隙圆度值；L为截面的孔隙边界总周长，mm；为该截面内孔隙包围的总面积，mm2，为截面编号。

扁平度特征值A表征滤层孔隙的狭长程度，是孔隙等效椭圆长轴和短轴的比值，表示孔隙等效椭圆接近理论圆的程度。计算公式如下：

式中A为滤层的孔隙扁平度值；R为截面孔隙等效椭圆的长轴，mm；R为该截面孔隙等效椭圆的短轴，mm。

1.4 计盒法计算滤层分形维数

分形理论在研究多孔介质砂滤层孔隙结构方面具有适用性[26]。通常采用分形维数表征孔隙结构的不确定性和变化规律，孔隙结构越规则，分形维数值越小。其中，计盒法计算分形维数最简单，物理意义较为明确。计盒维数的的计算过程如下[27]：

选取×像素的二值化CT切片图像为研究对象，黑色像素代表滤料颗粒。将图像用边长为k的网格进行划分，统计有黑色像素的网格的总数目Nk，即为非空盒子总数。当网格无限小时，lgNk与lg(1/)的比值逐步趋近于图像的计盒维数b，因此，对于递减的序列值{k}，可以在双对数坐标系中，采用最小二乘法拟合数据点（−lgk，lgNk）。

在保证相关系数足够大时，该斜率值即为计盒维数的近似值b。一般采用二等分法进行递减序列{k}的选取，即{，/2，/4，/8，/16，…}。

lgNk=·(−lgk)+（5）

沿试样高度方向每隔1 mm选取一张CT图像，经过数字化处理获得60张二值化图像，绘制盒子尺寸与盒子数目的双对数坐标关系图，从而得到每张CT二值化图中的计盒维数。对多张不同位置切片图像计算求平均值得到计盒维数均值。

式中D代表滤层试样的分形维数；为抽取的试样切片数量，D为单层切片图像的计算盒维数。

2 结果与分析

2.1 滤层孔隙率分布特征

通过截取的单元体切面的表观孔隙率，计算得到整个试样的各层表观孔隙率分布曲线如图6所示。由于切割间距较小，孔隙率的变化曲线具有连续性。从图6中可以看出，不同粒形滤料的滤层内部各横截面的表观孔隙率存在较大差异。在滤层表层部分，孔隙率偏大，随着滤层深度增加，孔隙率逐渐变小。分析原因是由于扫描试件滤料呈自由堆积状，滤料的不均匀以及滤层存在空间各向异性导致表观孔隙率的波动范围较大。在自由放置状态下，下层滤层由于受到挤压较大，孔隙率会相应较小，基本都在小于体积孔隙率计算值的范围内波动。

4种滤料QS1、SS2、MG3和GB4的表观孔隙率范围分别为39.7%～44.6%、38.5～42.3%、40.7%～45.6%、34.8%～38.7%，体积孔隙率计算值分别为42.2%、41.2%、44.1%、36.6%。从中可以发现，滤料形状棱角度越大，如QS1和MG3，表观孔隙率分布越分散，而粒形一致性较好的SS2和GB4，表观孔隙率的分布较为集中。根据文献[15]，采用注水法可获得滤层的实测孔隙率，石英砂QS1为0.429，海砂SS2为0.421，改性玻璃MG3为0.449，玻璃微珠GB4为0.379，比较实测孔隙率和计算体积孔隙率，两者之间具有较好的一致性，最大误差为3.43%。计算值普遍较实测值偏小，主要是因为在进行阈值分割时，将颗粒周围的阴影部分均被认定为颗粒，导致二值化后的计算表观孔隙率小于实际孔隙率，体积孔隙率也较实测孔隙率偏低。

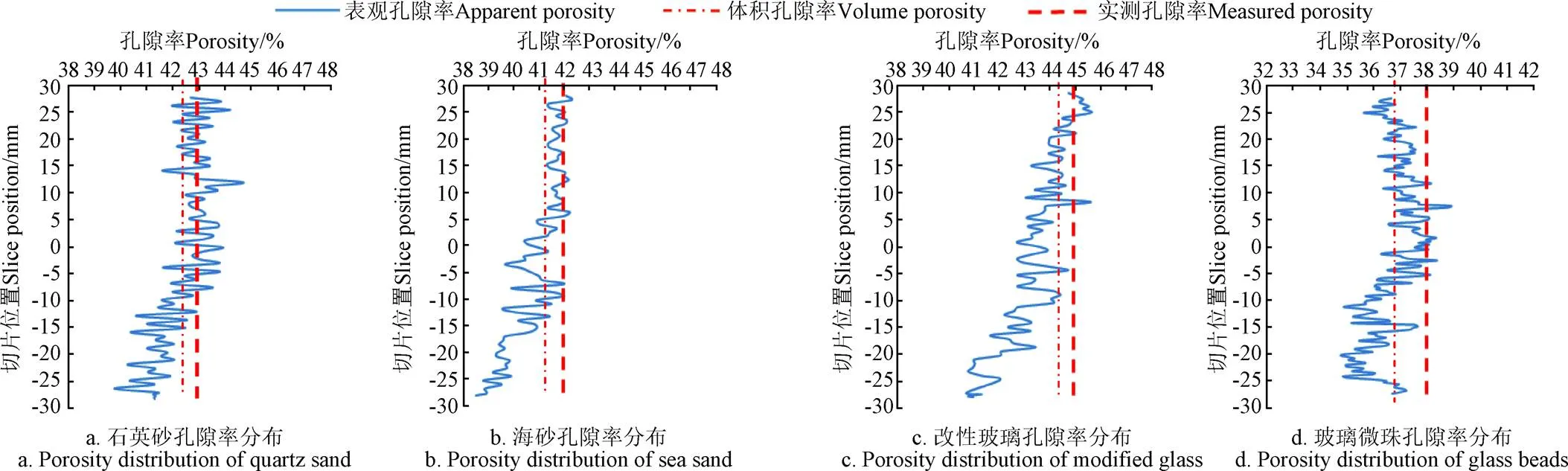
注：纵坐标所示位置为z轴位置。

2.2 滤层孔隙形状特征分析

2.2.1 孔径分布特征

通过VG Studio对 ROI 内的所有孔隙特征进行提取，统计分析孔径大小参数。4 种粒形滤料的孔隙分布趋势近似相同，小孔隙占多数，大孔隙占少数，其中，QS1 滤料的孔径范围是75～960m，SS2滤料为80～760m，MG3滤料为70～1 050m，GB4滤料为85～930m。对每种滤料的孔隙直径进行分组，比较其内部大、中、小孔隙分布特征，如表1。从表中可以看出，石英砂 QS1、海砂SS2的内部孔隙特征较为接近，大部分孔隙为小于75m的小孔隙，占比分别为65.65%和66.53%，改性玻璃MG3 小孔隙占比为63.42%，与石英砂、海砂差异不显著（<0.05），但是，大孔隙（150～1 000m）占比为17.24%，显著大于QS1（12.63%）和SS2（12.08%），大小孔隙占比变化代表了孔隙空间分布的变异性。而GB4滤料由于形状较为规则，内部孔隙分布较为均匀，大孔隙占比（31.29%）略低于小孔隙（42.75%）。

表1　不同滤层内孔隙分布特征表

注：表中数据为平均值±标准差，不同字母表示0.05水平下不同滤料间差异显著。

Note: The data in the table are the mean ± standard deviation, and different letters indicate significant difference between different filter medias at the level of 0.05.

2.2.2 孔隙形状分析

由图7a可得，各滤料试样的孔隙圆度值都大于1，分布在1.2～2.1之间，说明各滤层内部孔隙结构都比较偏离“圆形”孔隙，并且表现出圆度指标随着表观孔隙度指标的增加而增大，两者呈现正相关关系，决定系数2分别为0.973（QS1）、0.991（SS2）、0.995（MG3）、0.950（GB4）。通过计算，4种滤层不同深度切片孔隙圆度范围分别为1.59～1.78（QS1）、1.35～1.54（SS2）、1.65～2.03（MG3）、1.20～1.36（GB4）。

由图7b中看出孔隙扁平度R随孔隙率的变化规律，孔隙扁平度值变化区间在1.94～3.21之间，该值也表明滤层内部孔隙形状特征是以狭长状为主，而每种滤料滤层内部不同深度处的孔隙扁平度值R总体变化范围不大，4 种滤料R值范围分别为2.62～2.75（QS1）、2.05～2.20（SS2）、3.04～3.21（MG3）、1.94～2.04（GB4）。虽然整体上扁平度值变化不大，但是仍存在良好的规律性，均随孔隙率增加而增大。其中MG3的R值最大，主要是由于改性玻璃更为突出的棱角性，使得滤料之间呈现随机搭接状态，大量颗粒之间“点点接触”的嵌入挤压作用以及不均匀的细料填充，使得内部孔道错综复杂，很难产生较为圆润的孔洞，而是以封闭或者弯曲连通的孔道为主。滤料颗粒表面棱角性越强，内部孔道越狭长弯曲，狭长的孔道形态稳定，且较容易互相连通，为颗粒的运移和沉积提供了便利条件。

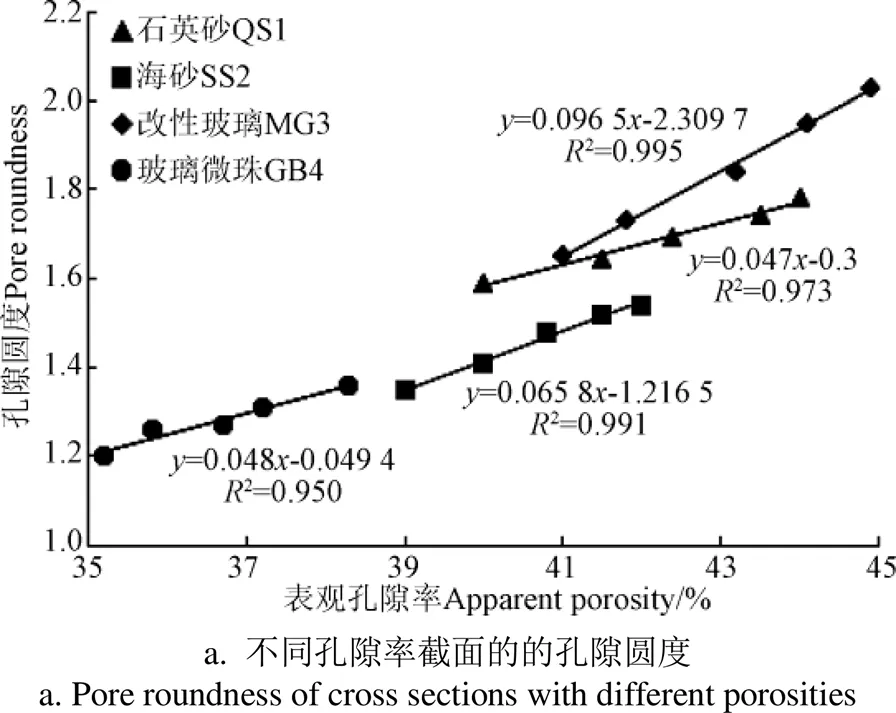
2.3 基于数字图像的滤层分形维数计算

图8为4种滤层单层切片图像处理后，获得的尺寸与盒子数目的双对数坐标关系图，拟合曲线斜率负值即为二维切片图像的分形维数。

注：横坐标代表盒子大小对数，纵坐标代表盒子数目对数。

经过统计分析后，绘制4种滤料60个CT样本图像的盒维数b值分布图，如图9。从图中可知，石英砂QS1盒子维数范围为1.574～1.649，平均值1.621；海砂SS2盒子维数范围为1.513～1.605，平均值为1.566；改性玻璃MG3盒子维数范围为 1.698～1.729，平均值为1.661；玻璃微珠GB4盒子维数范围为 1.414～1.484，平均值为1.446。盒子维数反映的是孔隙结构的复杂度和规则度，孔隙结构越规则，盒子维数值越小。同时从图中可以看出，随着切片位置从底部向顶部升高，分形维数值呈现总体减小趋势。

图9 不同深度切片盒维数分布规律

根据前面对滤层表观孔隙率的研究可知，随切片高度的升高，表观孔隙率呈现整体增加趋势。为了分析表观孔隙率与孔隙分形维数之间的关系，绘制QS1和SS2滤层表观孔隙率与盒维数分布规律关系图，如图10所示。可以看出，随着切面表观孔隙率的增加，滤层盒维数整体呈现减小趋势，滤层盒维数与表观孔隙率呈负相关关系，但盒维数对于表观孔隙率的变化并不敏感。可以看出，由于滤层厚度有限，因此表观孔隙率变动范围为10%左右，而滤层分维数变化幅度为4.24%。该结果与以往研究结果一致[28-30]，结合Sierpinski地毯确定型分形图案，认为由于分形维数f增加，固相分形体内的固相空间占比增加，而“孔”相中大尺寸孔隙数量相应减少，所以孔隙率增加。分形维数是滤层孔隙结构复杂程度和立体空间内纳污能力的表征，直接影响滤层的清洁压降及滤层渗透率等指标。

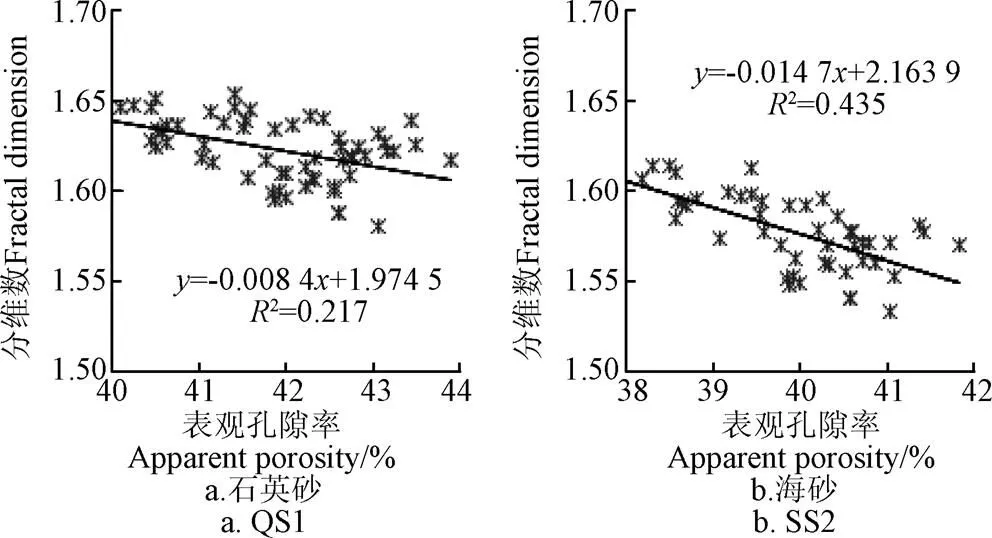
图10 切面表观孔隙率与分形维数关系

3 讨 论

以往对于滤层的研究，一般都是考虑滤层厚度（）、滤料粒径（）两个参数，然后通过滤层过滤前后的水质变化情况，间接反应滤层过滤性能[4]，这种研究手段并不能准确反应滤层的纳污能力和杂质分布特性。同时，同一种滤料如果材质不同，滤料棱角性也存在较大区别，滤料搭接构成的孔隙空间结构变异性较大，从而直接影响杂质颗粒的截留和运移特性[31]。要评价同一粒径不同粒形滤料的过滤反冲洗特性，首先要对不同粒形滤料滤层的孔隙结构特征进行量化，然后才能建立孔隙结构参数与过滤前后水质参数、纳污量、截留颗粒粒度分布等参数之间的相关关系[32]。本文采用CT扫描和数字图像处理技术对细观孔隙结构进行了建模和分析，研究结果实现了不同粒形滤料复杂孔隙结构的定量化表征，为传统的过滤堵塞毛细管理论模型的修正和校准提供数据支撑，为后续研究堵塞滤层内颗粒沉积和运移规律奠定基础。后续研究将继续参照本文研究方法，对堵塞后的滤层细观孔隙特征进行分析，探究滤层内部堵塞发生和变化机理。

4 结 论

1）不同粒形滤料组成的滤层各横截面表观孔隙率存在较大差异。表层滤层的孔隙率偏大，随着滤层深度增加，孔隙率逐渐变小。石英砂滤料（QS1）、海砂滤料（SS2）、改性玻璃滤料（MG3）、玻璃微珠滤料（GB4）的表观孔隙率范围分别集中在39.7%～44.6%、38.5%～42.3%、40.7%～45.6%、34.8%～38.7%，体积孔隙率计算值分别为42.2%、41.2%、44.1%、36.6%。滤料形状棱角度越大的，如QS1和MG3，表观孔隙率分布越分散，体积孔隙率越大。

2）4种不同粒形滤料的孔隙分布规律均是小孔隙占多数，大孔隙占少数，1.18 mm粒径滤层孔径分布区间为70～1 050m，且随着棱角度增加，大孔隙占比有所提高；滤层内部孔隙圆度值均大于1，分布在1.2～2.1之间，孔隙扁平度值分布区间为1.94～3.21，即4种滤料的孔隙形状均以狭长型为主，滤层孔隙率与圆度值、扁平度均成正相关关系。

3）基于二值化CT切片图像的4种滤层孔隙结构的计盒维数均值分别为1.621（QS1）、1.566（SS2）、1.661（MG3）和1.446（GB4），表明棱角度越高、孔隙结构越复杂，同时分形维数还与孔隙率有关，两者呈负相关关系，但分形维数对于孔隙率变化并不敏感。

[1] 李仰斌，刘俊萍. 中国节水灌溉装备与技术发展展望[J]. 排灌机械工程学报，2020，38(7)：738-742.

Li Yangbin, Liu Junping, Development prospect of water- saving irrigation equipment and technology in China[J]. Journal of Drainage and Irrigation Machinery Engineering, 2020, 38(7): 738-742. (in Chinese with English abstract)

[2] Tarjuelo J M, Rodriguez-Diaz J A, Abadia R, et al. Efficient water and energy use in irrigation modernization: Lessons from Spanish case studies[J]. Agricultural Water Management, 2015, 162: 67-77.

[3] 翟国亮，陈刚，赵红书，等. 微灌用均质砂滤料过滤粉煤灰水时对颗粒质量分数与浊度的影响[J]. 农业工程学报，2010，26(12)：13-18.

Zhai Guoliang, Chen Gang, Zhao Hongshu, et al. Effects of filter with uniform sandy filtration medium used in micro-irrigation on mass fraction of particles and turbidi- ty of water with fly ash[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(12): 13-18. (in Chinese with English abstract)

[4] Cescon A, Jiang J Q. Filtration Process and Alternative Filter Media Material in Water Treatment[J]. Water, 2020, 12(12): 3377.

[5] Haman D Z, Smajstrla A G, Zazueta F S. Media filters for trickle irrigation in Florida[R]. Department of Agricultural and Biological Engineering, UF/IFAS Extension, 2017.

[6] Goyal Megh. Management of Drip/Trickle or Micro Irrigation[M]. Canada:Apple Academic Press Inc., 2012.

[7] Mesquita M, Testezlaf R, Diotto A V. Removal efficiency of pressurized sand filters during the filtration process[J]. Desalination and Water Treatment, 2019, 161:132.

[8] Kandra H S, Mccarthy D, Fletcher T D, et al. Assessment of clogging phenomena in granular filter media used for stormwater treatment[J]. Journal of Hydrology, 2014, 512: 518-527.

[9] Mcgivney W, Kawamura S. Cost estimating manual for water treatment facilities[J]. Asia Pacific Biotech News, 2008, 11(18): 1186-1191.

[10] 张宇. 均质滤料过滤技术研究-滤料粒径和滤层厚度对过滤特性的影响关系研究[D]. 西安：西安建筑科技大学，2004.

Zhang Yu. Study on Filtration with Uniform Media—the Influence of Media’s Diameter and Depth on Filtration Performance[D]. Xi’an: Xi’an University of Architecture and Technology, 2004. (in Chinese with English abstract)

[11] 张建锋，张栋喆，周超，等. 滤层配置特征对砂滤池过滤性能的影响[J]. 西安建筑科技大学学报（自然科学版），2014，46(5)：5.

Zhang Jianfeng, Zhang Dongzhe, Zhou Chao, et al. Effect of filter media configuration characteristics on the performance efficiency in quartz sand filter[J]. Journal of Xi´an University of Architecture and Technology (Natural Science edition), 2014, 46(5): 5. (in Chinese with English abstract)

[12] 张文正，蔡九茂，吕谋超，等．砂石过滤器过滤效果影响因素试验研究[J]. 灌溉排水学报，2020，39(7)：77-83.

Zhang Wenzheng, Cai Jiumao, Lv Mouchao, et al. Experimental study on influencing factors of filtration effect of sand filter[J]. Journal of Irrigation and Drainage, 2020, 39(7): 77-83. (in Chinese with English abstract)

[13] Soyer E, Akgiray M, Eldem N Z, et al. Crushed recycled glass as a filter medium and comparison with silica sand[J]. Clean-Soil Air Water, 2010, 38(10): 927-935.

[14] Kandra H, Mccarthy D, Deletic A. Assessment of the impact of stormwater characteristics on clogging in stormwater filters[J]. Water Resources Management, 2015, 29(4): 1031-1048.

[15] Bové J, Arbat G, Duran-Ros M, et al. Pressure drop across sand and recycled glass media used in micro-irrigation filters[J]. Biosystems Engineering, 2015, 137: 67-78.

[16] 刘泉声，崔先泽，张程远. 多孔介质中悬浮颗粒迁移—沉积特性研究进展[J]. 岩石力学与工程学报，2015，34(12)：2410-2427.

Liu Quansheng, Cui Xianze, Zhang Chengyuan. Research advances in the characterization of transportation and deposition of suspended particles in porous media[J]. Journal of Rock Mechanics and Engineering, 2015, 34(12): 2410-2427. (in Chinese with English abstract)

[17] Ahfir N D , Hammadi A , Alem A , et al. Porous media grain size distribution and hydrodynamic forces effects on transport and deposition of suspended particles[J]. Journal of Environmental Sciences, 2017, 53(3): 161-172.

[18] 刘泉声，崔先泽，张程远，等. 粒径对多孔介质中悬浮颗粒迁移：沉积特性的影响[J]. 岩土工程学报，2014，36(10)：1777-1783.

Liu Quansheng, Cui Xianze, Zhang Chengyuan, et al. Effects of particle size on characteristics of transportation and deposition of suspended particles in porous media[J]. Journal of Rock Mechanics and Engineering, 2014, 36(10): 1777-1783. (in Chinese with English abstract)

[19] 陈星欣，白冰，于涛，等. 粒径和渗流速度对多孔介质中悬浮颗粒迁移和沉积特性的耦合影响[J]. 岩石力学与工程学报，2013，32(S1)：2840-2845.

Chen Xingxin, Bai Bing, Yu Tao, et al. Coupled effects of particle size and flow rate on characteristics of particle transportation and depositon in porous media[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S1): 2840-2845. (in Chinese with English abstract)

[20] 蒋思晨，白冰. 悬浮颗粒形状对其在多孔介质中迁移和沉积特性的影响[J]. 岩土力学，2018，39(6)：2043-2051.

Jiang Sichen, Bai Bing. Influence of particle shape on the suspended particle transport and deposition in porous media[J]. Rock and Mechanics, 2018, 39(6): 2043-2051. (in Chinese with English abstract)

[21] 程亚南，刘建立，吕菲，等. 基于CT图像的土壤孔隙结构三维重建及水力学性质预测[J]. 农业工程学报，2012，28(22)：115-122.

Cheng Yanan, Liu Jianli, Lv Fei, et al. Three-dimensional reconstruction of soil pore structure and prediction of soil hydraulic properties based on CT images[J]. Transactions of the Chinese Society Agricultural Engineering (Transaction of the CSAE), 2012, 28(22): 115-122. (in Chinese with English abstract)

[22] 邱琛，韩晓增，陈旭，等. CT扫描技术研究有机物料还田深度对黑土孔隙结构影响[J]. 农业工程学报，2021，37(14)：98-107.

Qiu Chen, Han Xiaozeng, Chen Xu, et al. Effects of organic amendment depths on black soil pore structure using CT scanning technology[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(14): 98-107. (in Chinese with English abstract)

[23] 赵冬，许明祥，刘国彬，等. 用显微CT研究不同植被恢复模式的土壤团聚体微结构特征[J]. 农业工程学报，2016，32(9)：123-129.

Zhao Dong, Xu Mingxiang, Liu Guobin, et al. Characterization of soil aggregate microstructure under different revegetation types using micro-computed tomography[J]. Transactions of the Chinese Society Agricultural Engineering (Transaction of the CSAE), 2016, 32(9): 123-129. (in Chinese with English abstract)

[24] 王金波. 岩石孔隙结构三维重构及微细观渗流的数值模拟研究[D]. 北京：中国矿业大学，2014.

Wang Jinbo. 3D Reconstruction of Porous Rock and Numerical Simulations of Fluid Flow at Mesoscale Levels[D]. Beijing: China University of Mining and Technology, 2014. (in Chinese with English abstract)

[25] 肖楠. 岩石孔隙结构三维随机重构研究[D]. 重庆：重庆大学，2018.

Xiao Nan. Study on Three Dimension Mathematical Physical Reconstruction of Pore Structure in the rock[D]. Chongqing: Chongqing University, 2018. (in Chinese with English abstract)

[26] 李丹，汪洪平，张超，等. 基于CT扫描的尾矿细观结构表征研究[J]. 武汉大学学报（工学版），2020，53(7)：574-582.

Li Dan, Wang Hongping, Zhang Chao, et al. Study on meso-structure characteristics of tailings based on CT scanning[J]. Engineering Journal of Wuhan University, 2020, 53(7): 574-582. (in Chinese with English abstract)

[27] 李景海，翟国亮，刘清霞，等. 基于分形维数特征的砂滤层适宜粒径范围[J]. 农业工程学报，2021，37(20)：162-168.

Li Jinghai, Zhai Guoliang, Liu Qingxia, et al. Suitable particle size range of sand filter layers based on fractal dimension characteristics[J]. Transactions of the Chinese Society Agricultural Engineering (Transaction of the CSAE), 2021, 37(20): 162-168. (in Chinese with English abstract)

[28] 彭瑞东，杨彦从，鞠杨，等. 基于灰度CT图像的岩石孔隙分形维数计算[J]. 科学通报，2011，56(26)：2256-2266.

Peng Ruidong, Yang Yancong, Ju Yang, et al. Calculation of fractal dimension of rock pore based on gray CT image[J]. Chinese Science Bulletin, 2011, 56(26): 2256-2266. (in Chinese with English abstract)

[29] 雷蕾. 基于计算模拟和溶蚀实验的碳酸盐岩孔隙定量表征及孔隙演化特征研究[D]. 武汉：中国地质大学，2019.

Lei Lei. Quantitative Characterization and Pore Structure Evolution of Carbonate Reservoir Based on Computational Simulation and Dissolution Experiment[D]. Wuhan: China University of Geosciences, 2019. (in Chinese with English abstract)

[30] 张巍，梁小龙，唐心煜，等. 显微CT扫描南京粉砂空间孔隙结构的精细化表征[J]. 岩土工程学报，2017，39(4)：683-689.

Zhang Wei, Liang Xiaolong, Tang Xinyu, et al. Fine characterization of spatial pore structure of Nanjing silty sand using micro-CT[J]. Journal of Rock Mechanics and Engineering, 2017, 39(4): 683-689. (in Chinese with English abstract)

[31] 杨保华，吴爱祥，缪秀秀，等. 基于CT图像的矿石颗粒堆积体孔隙结构三维量化表征和分析[J].中国有色金属学报（英文版），2014，24(3)：833-838.

Yang Baohua, Wu Aixiang, Miu Xiuxiu, et al. 3D characterization and analysis of porestructure of packed ore particle beds based on computed tomography images[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(3): 833-838. (in English with Chinese abstract)

[32] 丁自伟，李小菲，唐青豹，等. 砂岩颗粒孔隙分布分形特征与强度相关性研究[J]. 岩石力学与工程学报，2020，39(9)：1787-1796.

Ding Ziwei, Li Xiaofei, Tang Qingbao, et al. Study on correlation between fractal characteristics of pore distribution and strength of sandstone particles[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(9): 1787-1796. (in Chinese with English abstract)

Pore structure characteristics of different granular filter media based on CT scanning

Cai Jiumao1, Song Lei1, Zhang Wenzheng1, Zhai Guoliang1※, Xu Qiang2, Li Penglai3

(1./,453002; 2.243071,; 3.024005,)

Sand media filters are often among the common filter modes in micro-irrigation system due to its excellent fouling capacity. The sand filter intercepts impurity particles mainly through the filter layer pores. The pore structure of filter layers directly affects the effect of particle deposition and transport during filtration .The objective of this work was to to master the internal pore structure characteristics of sand filter layers composed of different granular filter media. Taking ordinary Quartz Sand(QS1), Sea Sand(SS2), ASM Modified Glass(MG3) and Glass Beads(GB4) with selected grain size1.0～1.18 mm as research objective, this study employs the advanced CT scanning technique to construct the three-dimensional(3D) structure of four filter layers. In combination with image analysis software VGStudio MAX, Image J, et al, the pore structure parameters such as porosity, pore size distribution, pore roundness value and flatness ratio of four filter layers were obtained by processing different filter layer CT slices. In order to investigate the complexity of different layer pore structure, the box-counting fractal dimensions of pore structures were calculated with fractal theory. The research results showed that the apparent porosity range of the four filter layers were 39.7%-44.6% (QS1), 38.5%-42.3%(SS2), 40.7%-45.6%(MG3), 34.8%-38.7%(GB4) and the volume porosities were 42.2%, 41.2%, 44.1%, 36.6% respectively. The pore size intervals were 75-960, 80-760, 70-1 050, 85-930m and the difference was not significant. The calculated pore roundness value ranges were 1.59-1.78, 1.35-1.54, 1.65-2.03, 1.20-1.36, the pore flatness ranges were 2.62-2.75, 2.05-2.20, 3.04-3.21, 1.94-2.04, the fractal dimensionsbof the four filter layers were 1.621, 1.566, 1.661 and 1.446, respectively. This study quantitatively characterized the pore structure characteristics of the filter layer, and obtained the differences of meso-pore structure of different granular filter media. The apparent porosities of the top filter layers were more higher than that of the bottom layers along the depth of the filter. The pore size distribution law was that small pores (<75m) accounted for the majority for all the four granular media and the pore shapes were mainly narrow and long type. With the media particle angularity increase, the distribution of the apparent porosity was more dispersed and the volume porosity was higher, the proportion of macro-pores increased accordingly and the maximum value reached 17.24% for MG3. The tendency of pore shape parameters deviation from sphericity was more obvious. The fractal box-counting dimension, which represented the complexity of pore structure, increased with the media angularity accordingly, and fractal dimension was negatively correlated with apparent porosity. The quantitative analysis of filter layers pore structure can overcome the shortage of traditional model experiment and provide a foundation for the subsequent study of particle deposition and migration in the filter layers.

micro-irrigation; CT images; image processing; pore structure; porosity; fractal dimension

10.11975/j.issn.1002-6819.2022.19.011

S275.5

A

1002-6819(2022)-19-0094-08

蔡九茂，宋蕾，张文正，等. 基于CT扫描的不同粒形滤料孔隙结构特征[J]. 农业工程学报，2022，38(19)：94-101.doi：10.11975/j.issn.1002-6819.2022.19.011 http://www.tcsae.org

Cai Jiumao, Song Lei, Zhang Wenzheng, et al. Pore structure characteristics of different granular filter media based on CT scanning[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(19): 94-101. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.19.011 http://www.tcsae.org

2022-01-25

2022-09-20

河南省重大科技专项项目“小麦全产业链融合发展关键技术研发与示范应用”（221100110700）；新乡市重大科技专项“智慧灌溉系统装备研发”（ZD2020009-03）

蔡九茂，博士，副研究员，研究方向为微灌技术理论与应用。Email：caijiumao@163.com

翟国亮，博士，研究员，博士生导师。研究方向为微灌技术理论与应用。Email：zhai3393@126.com