地下结构地震反应的平面计算模型研究1
2022-02-03楼梦麟蔡海兵
殷 琳 舒 恩 楼梦麟 蔡海兵
1)宁波工程学院, 建筑与交通工程学院, 浙江宁波315211
2)安徽理工大学, 土木建筑学院, 安徽淮南232001
3)同济大学, 土木工程学院, 上海200092
引言
有限元法是地下结构地震反应分析的常用方法(刘晶波等,2006;杜修力等,2017;陈国兴等,2019),采用有限元法对地下结构进行地震反应分析时,通常将三维模型简化为平面应变模型进行计算(王国波等,2015;庄海洋等,2019)这是因为地震时,地下结构横断面变形以平面内的剪切变形为主(Hashash 等,2001),平面应变模型适合描述此变形模式,且地下结构动力分析模型涉及一定范围的土体,三维数值模型自由度大,计算耗时长,对计算设备要求高。
将地下结构地震反应分析的有限元模型简化为二维平面应变模型时,核心问题是中柱的模拟,即将中柱三维空间梁简化为二维平面梁时,相关力学参数合理等效问题。韩文星(2005)和田雪娟(2010)对该问题进行了研究,虽对简化模型相关参数取值问题进行了说明,但未分析简化后模型的计算误差水平,其他学者采用二维平面应变模型进行分析时也存在同样的问题。
本文以大开地铁车站为例,分别建立二维和三维有限元模型,对地铁车站结构进行地震反应计算,并以三维模型的计算结果作为对比基准,分析不同二维简化模型计算误差,讨论不同简化方法的合理性。
1 地下结构中柱简化方法
1.1 现行方法
关于中柱等效二维平面应变的等效问题,目前常用以下方法:
(1)方法1:调整弹性模量(庄海洋等,2009)
通过调整弹性模量,保证中柱等效前、后的抗弯刚度相同,弹性模量调整系数取为中柱纵向间距的倒数,弹性模量调整公式为:

式中,E∗为等效后中柱弹性模量;α1为弹性模量调整系数,取中柱纵向间距的倒数;E为等效前中柱弹性模量。
(2)方法2:调整弹性模量和密度(杜修力等,2018)
通过调整弹性模量和密度,保证中柱等效前、后的截面抗弯刚度和质量均相同,弹性模量和密度调整系数均取为中柱纵向间距的倒数,弹性模量调整公式如式(1)所示,密度调整公式为:

式中, ρ∗为等效后中柱密度;α2为密度调整系数,取中柱纵向间距的倒数,数值上等于α1;ρ为等效前中柱密度。
1.2 本文建议方法
为合理建立等效简化模型,应考虑以下因素:
(1)对中柱横向刚度、密度和阻尼特性等动力特性进行等效。地下结构二维平面应变模型相当于平面模型沿纵向连续,且纵向尺寸为单位长度,因此将中柱弹性模量除以中柱纵向间距等效其横向刚度,这是现行方法1 采用的等效方法。将中柱弹性模量除以中柱纵向间距等效其横向刚度,同时将中柱密度除以中柱纵向间距等效中柱密度,这是现行方法2 采用的等效方法,本文采用该等效方法。由于考虑材料阻尼特性时,目前一般采用无量纲参数阻尼比,可不进行调整。
(2)从有限单元建模角度来看,二维梁单元是在三维梁单元的基础上,每个结点增加了3 个自由度的约束,2 个结点的梁单元共增加了沿纵向的6 个自由度的约束,从而增大了整体刚度。为降低刚度增大带来的影响,对材料弹性模量再乘以1 个调整系数,本文称该系数为空间约束影响系数,通过多次计算,建议该系数取为0.8。
(3)求解得到二维平面应变模型的地震反应后,需还原至三维模型。采用二维平面应变模型求解得到中柱端部截面内力(弯矩、剪力和轴力)后,应乘以相应系数得到三维模型中柱端部截面的真实内力。因二维平面应变模型相当于沿地下结构纵向取单位长度的范围,而实际上地震发生时,无论是水平还是垂直分量,每根中柱承担的地震作用范围应为中柱的纵向间距,所以真实的中柱截面内力应为二维模型所得结果再乘以数值上等于中柱纵向间距的系数,该系数称为三维还原调整系数,真实的中柱端部截面内力计算公式为:

式中,S∗为真实的中柱截面内力效应,包括柱端弯矩、剪力和轴力;α3为 三维还原系数,取中柱纵向间距;S为二维等效模型所得的中柱截面内力效应。
本文建议的中柱二维等效方法称为方法3。
1.3 影响因素分析
为分析不同影响因素在二维等效模型中的影响程度,将三维还原调整因素引入到方法1 和方法2 中,即将方法1 和方法2 的计算结果乘以三维还原系数 α3,分别称为方法1a 和方法2a,将方法3 计算结果与方法1 和方法2 计算结果进行对比,总体上可判断本文建议方法的合理性。同时,根据方法2a 与方法1a 的对比结果可知质量密度调整系数的影响程度,根据方法3 与方法2a 的对比结果可知空间约束因素的影响程度。
2 算例分析
本文以大开地铁车站为例,说明3 种不同中柱等效方法的合理性。大开地铁车站为单层双跨框架式结构,埋深4.8 m,横断面尺寸如图1 所示,横断面宽17 m,高7.17 m,侧壁厚0.85 m,顶板厚0.80 m,底板厚0.85 m。车站周围土层物理性质如表1 所示(曹炳政等,2002)。计算时忽略土体的非线性特性及车站与土体的接触非线性。
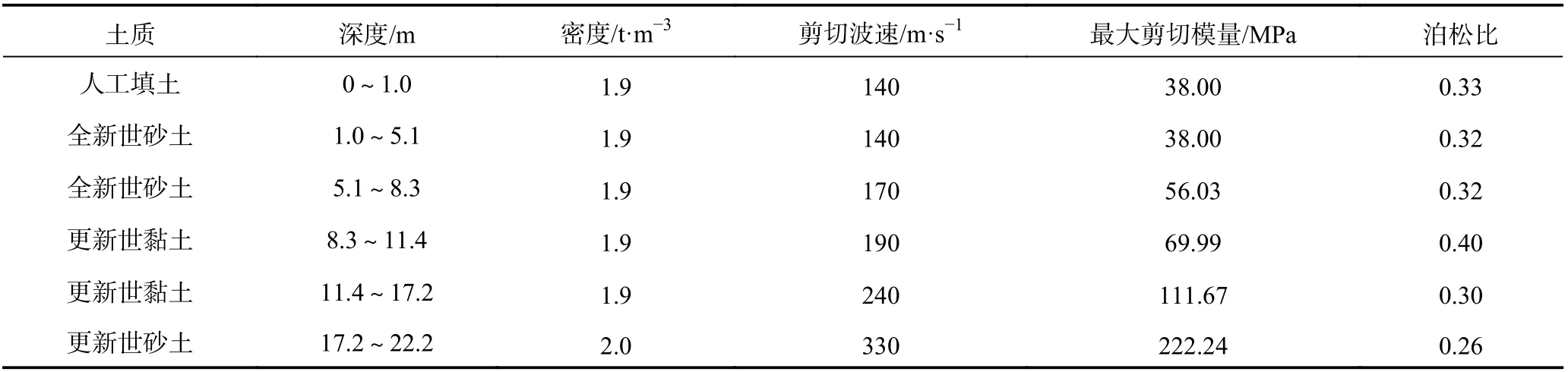
表1 场地土物理力学参数Table 1 Physical parameters of site soil properties
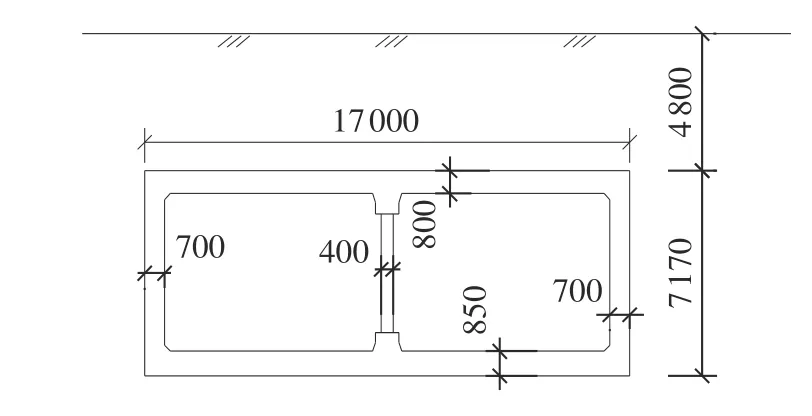
图1 大开地铁车站结构横断面(单位:毫米)Fig. 1 Cross section of Subway station(Unit: mm)
2.1 二维有限元计算模型
为尽可能减小土层人工边界反射效应的影响,根据楼梦麟等(2016)的建议,建立二维有限元模型时,在地下结构两侧向外取5 倍土层深度的有限土层,竖向人工边界设置为能够保证土层沿横向水平剪切位移的侧移边界(透射边界)。竖向范围取至第6 层土底部至基岩面,该底部结点约束全部自由度,作为横向水平地震的输入面。
为在振动分析中防止有限单元竖向尺寸的滤波效应对地震反应计算结果准确性的影响,土层有限元网格的竖向尺寸按最高有效截止频率为25 Hz 的正弦波对应波长的1/16~1/8 控制,单元横向尺寸不超过竖向的4 倍。
地下结构侧壁和中柱采用二维梁单元离散,地下结构周围土层采用四边形等参元离散,离散后二维模型共有6 356 个四边形等参元、69 个二维梁单元、6 592 个结点,施加边界条件后共有12 860 个自由度。二维模型的有限元网格示意如图2 所示。
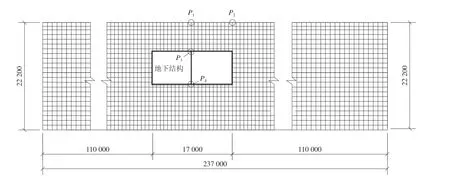
图2 有限元网格示意与监测点位置(单位:毫米)Fig. 2 The mesh of finite element and observation points(Unit: mm)
2.2 三维有限元计算模型
为保证三维和二维计算模型一致,三维模型在竖平面中的计算范围和网格尺寸与二维模型保持一致。另外,在纵向取7 跨中柱的地下结构和相应的有限土层,纵向有限元网格尺寸与横向一致。四边的竖向人工边界设置为能够保证土层沿横向水平剪切位移的侧移边界。
三维模型中,地下结构侧壁和顶、底板采用三维板单元离散,中柱采用三维梁单元离散,土体采用八结点六面体等参元离散,离散后三维模型共有10 136 个板单元、165 个三维梁单元、444 920 个八结点六面体等参元、467 192 个结点,施加边界条件后共有1 381 252 个自由度。有限元模型两侧结点约束垂向和纵向自由度,底部结点约束全部自由度,同时作为地震激励的输入面。
3 输入地震波及其频谱特性
本文选择了3 条有代表性的基岩波作为激振地震波,分别为某大型工程场地安全性评价得到的基岩人工波、阪神地震中神户大学记录的Kobe 波和汶川地震中四川郫县走石台记录的基岩波,分别称之为JY 波、Kobe 波和WC 波,峰值加速度分别为1.00、0.27、1.20 m/s2,加速度时程、傅里叶幅值谱和反应谱如图3所示。
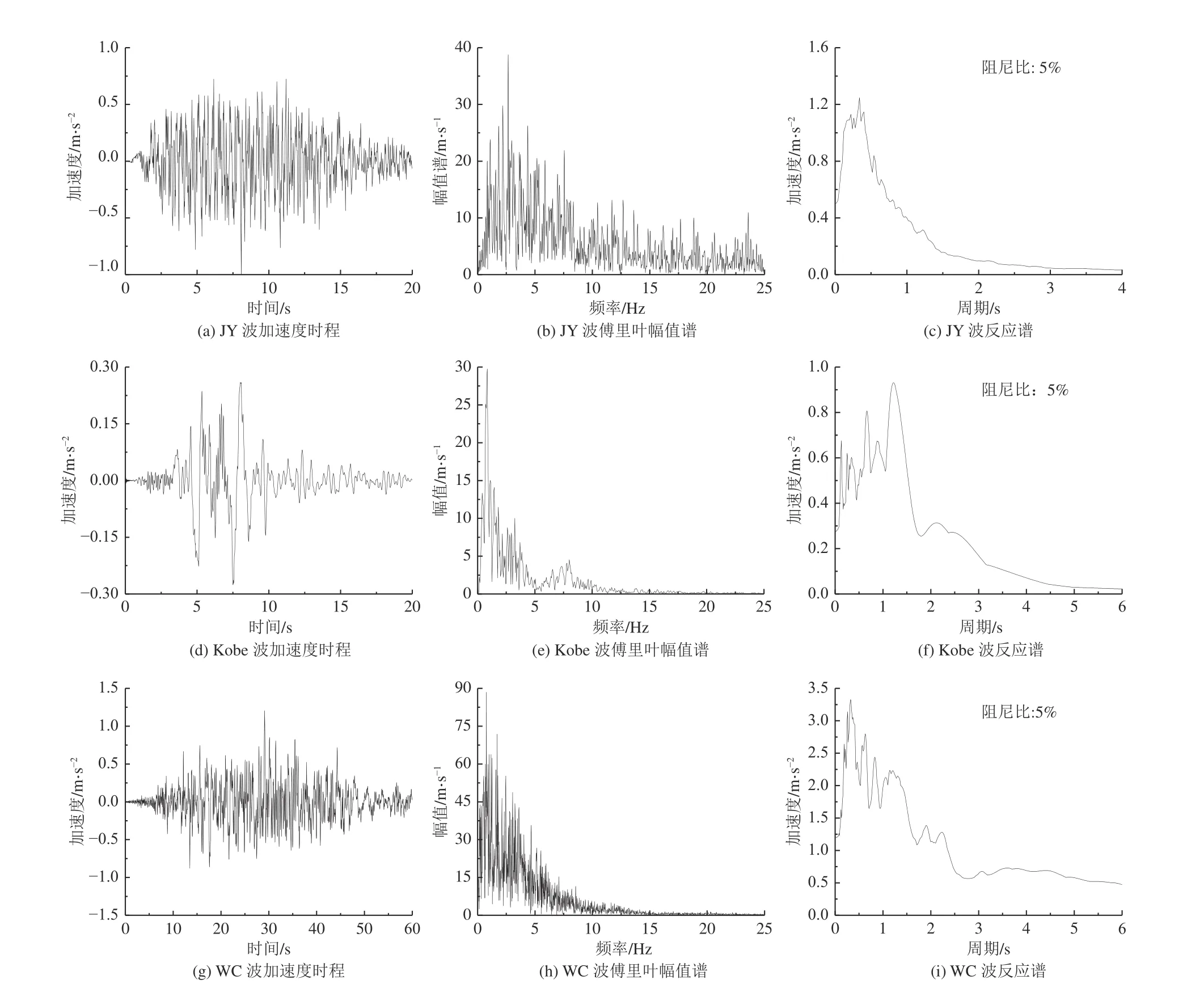
图3 地震波加速度时程、傅里叶幅值谱和反应谱Fig. 3 Time history of exciting and its Fourier spectrum and its response spectrum
4 基本运动方程
二、三维模型各部分采用合适的有限单元离散后的运动方程为:

式中,u(t) 、u˙(t)和u¨(t)分 别为体系各自由度的相对位移、相对速度和相对加速度反应列向量;u¨g(t)为基岩运动加速度向量;m、c和k分别为有限元离散后的质量矩阵、阻尼矩阵和刚度矩阵。
采用逐步积分求解运动方程可得各自由度基本未知量,如位移、速度和加速度反应时程。由基本未知量可计算其他反应量,如梁单元的弯矩、剪力和轴力,实体单元的应力、应变等。
5 结果分析
三维模型模态分析结果如表2 所示。根据各阶振型的横向(水平向)参与系数和计算所得振型可知,第1 阶和第7 阶是前2 个横向(水平向)的剪切振型,其频率分别为2.66、2.89 Hz。

表2 三维模型的前7 阶自振频率及横向(水平向)振型参与系数Table 2 The first seven natural frequencies of three dimension model and modal participation factor of horizontal direction
二维模型模态分析结果如表3 所示,根据各阶振型的横向(水平向)参与系数和计算所得振型可知,第1 阶和第3 阶是前2 个横向(水平向)的剪切振型,其频率分别为2.64、2.87 Hz。

表3 二维模型的前7 阶自振频率及横向(水平向)振型参与系数Table 3 The first seven natural frequencies of two dimension model and modal participation factor of horizontal direction
时程分析时,选用Rayleigh 比例阻尼作为阻尼模型,因本文算例的基频较高,Rayleigh 阻尼系数的计算采用系统前2 个水平剪切振动模态对应的圆频率(舒恩,2020),即计算阻尼系数时,三维模型采用2.66、2.89 Hz,二维模型采用2.64、2.87 Hz。
三维和二维简化模型计算得到的地震反应分别如表4 和表5 所示。表4 中中柱地震反应未列出轴力,是因为单层双跨结构在仅有水平地震作用下可认为是反对称结构,中柱近似无轴力(许紫刚等,2019)。
由表4 可知,无论是何种地震波激励,方法3 均优于方法1 和方法2。需注意,方法1 和方法2 计算结果均为负误差,说明计算结果偏小,从工程安全性角度评价,方法1 和方法2 偏于不安全。方法1 和方法2计算误差水平相当,方法1 所得柱顶计算结果误差略大于方法2,但所得柱底计算结果误差略小于方法2,说明材料密度的等效对中柱地震反应的影响较小。方法1a 的计算误差明显小于方法1,且方法2a 的计算误差明显小于方法2,说明二维模型计算结果不能直接等效为三维真实情况,借用方法3 的三维还原系数可改善相应的计算精度。方法3 计算误差明显小于方法2a,说明空间约束因素对中柱计算结果有较大影响。
由表4 和表5 可知,本文采用的3 种二维等效模型对地下结构整体的运动反应影响较小,因采用平面应变问题求解地下结构的横向水平地震反应在力学基本原理上符合工程实际情况,但由于中柱平面应变等效是人为的主观假定,因此不同方法下计算得到的中柱截面内力相差较大,相比之下,方法3 的近似计算精度远高于方法1 和方法2。从本文算例结果来看,无论采用哪种方法,计算得到的加速度和位移误差水平相近,位移和加速度反应误差均在13%以内,当采用方法3 时,柱弯矩和剪力误差≤7%,较方法1 和方法2 得到了明显改进。

表4 中柱地震反应峰值Table 4 Peak seismic response of the inner column
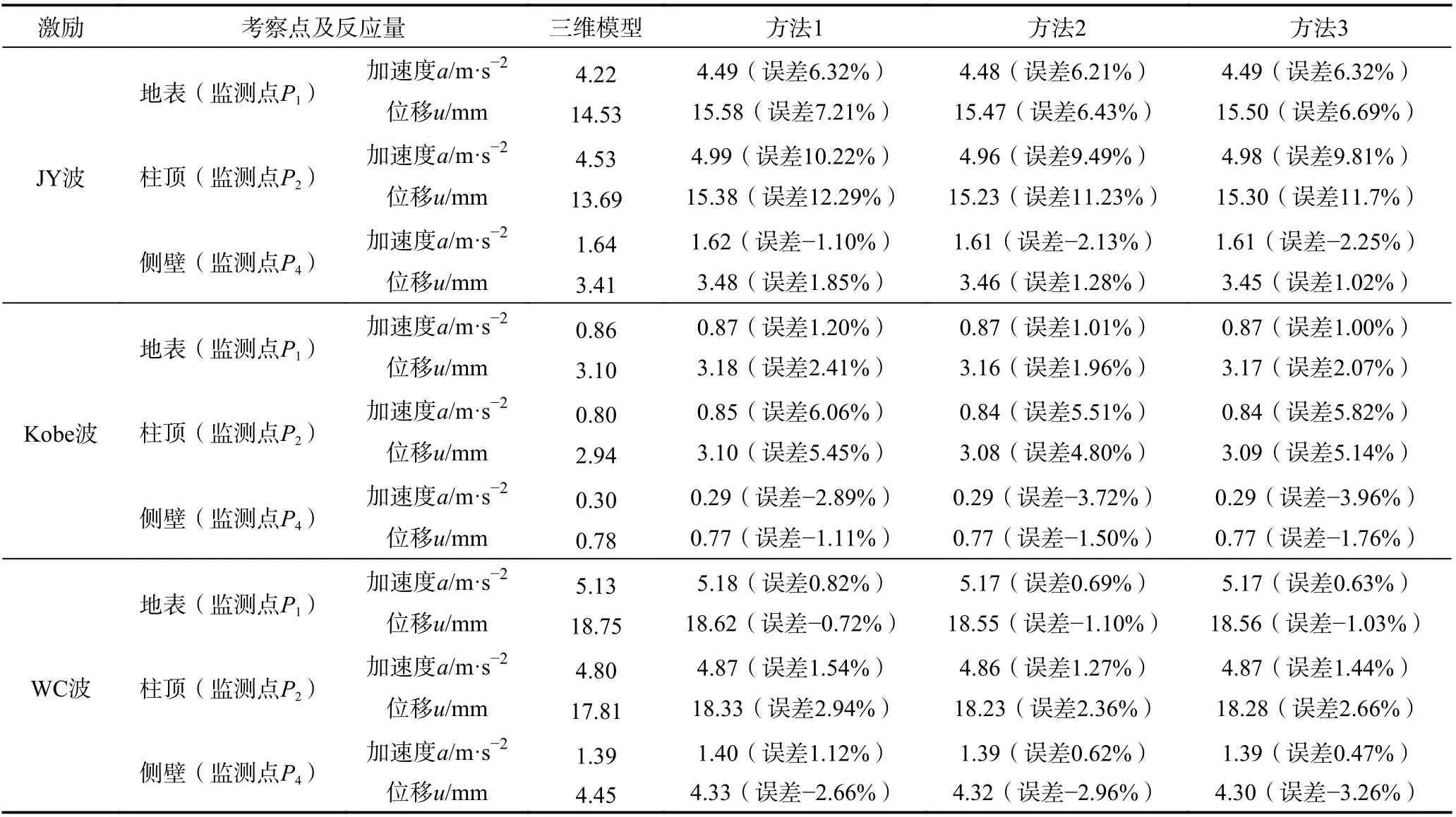
表5 关键点地震反应峰值Table 5 Peak seismic response of observation points
6 结论
(1)对地下结构进行地震反应分析时,可将三维模型简化为平面应变二维模型进行计算。简化时应重点关注结构中柱的等效方法,如果简化方法选择不当,可能会给地下结构内力计算带来较大误差,应重视中柱的等效问题。
(2)现行简化方法1 和方法2 会低估中柱地震反应,最大低估程度可达77.24%,从工程安全性角度评价,方法1 和方法2 偏于不安全。本文提出的方法3 可明显减小中柱地震反应误差,使中柱弯矩和剪力误差≤7%。
(3)方法1、方法2 和方法3 均可得到误差较小的加速度和位移反应,3 种方法误差水平相近,方法3可使加速度和位移计算误差≤13%。
