改进用户评分相似度的协同过滤推荐算法

王诗淞，刘伟哲，孙雪莲

（大连民族大学理学院，大连 116650）

0 引言

现如今，随着计算机硬软件技术的高速发展，数据规模呈现爆发式增长的趋势，带来了严重的“信息超载”问题［1］，而个性化推荐算法成为解决这一问题的主要方式。凭借着原理较为简单、可解释性较强等优点，协同过滤算法成为应用最广泛、最成功的推荐算法［2］。其中最常用的三种协同过滤算法为基于用户的协同过滤［3］、基于项目的协同过滤［4］、基于模型的协同过滤［5］。基于用户的协同过滤推荐算法作为本文主要的研究算法，相似度计算作为其核心，其好坏直接影响着推荐结果。而在实际中，项目和用户数量的庞大都会使评分矩阵变稀疏，从而影响推荐准确度。

为了解决上述问题，大量学者提出创新与改进。吴锦昆等［6］提出一种引入用户差异因子的皮尔逊相似度计算方法，解决用户在不同评价体系中存在偏差的问题。潘锦丰等［7］提出一种相似度修正参数并与基于用户属性特征向量相融合，以此改进相似度计算方法，解决用户属性存在偏差的问题。魏浩等［8］提出一种基于用户与项目特征兴趣的相似度算法，通过生成项目特征兴趣矩阵提升推荐的准确率。李港［9］将用户评分信息熵与改进的皮尔逊相似度计算方法相融合，形成一种新的相似度计算方法，提升了用户之间相似度的精确性。

上述研究工作虽在一定程度上提高了相似度计算的准确性与推荐精度，但并不能很好地解决共同评分集合的数量差异、用户评分数值差异、项目热门度差异和用户兴趣随时间因素变化差异的问题。因此，本文提出一种融合权重因子、修正因子与时间衰减因子的改进用户相似度的协同过滤算法（IMPCOS-CF），以提升用户相似度的准确率与推荐算法的性能。

1 传统相似度计算方法

1.1 余弦相似度

余弦相似度（Cosine Similarity），也称为余弦距离，它通过计算两个向量之间的夹角对应的余弦值来衡量二者间差异的标准［10］。计算公式如式（1）所示：

1.2 Pearson相关系数

Pearson 相关系数表示两个随机变量之间的相关程度，它的取值范围为［-1，1］，其绝对值越大，则两个随机变量之间的相关性就越强［11］。计算公式如式（2）所示：

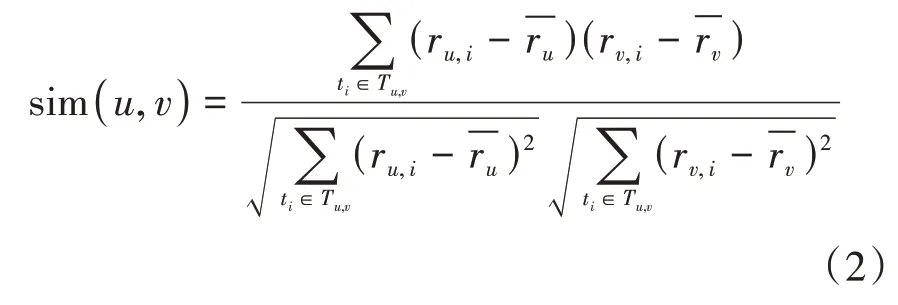
1.3 修正余弦相似度

修正余弦相似度（Adjust Cosine Similarity）在计算中考虑到评分偏向对评分所造成的影响与评分尺度［12］，使得相似度度量更加合理。计算公式如式（3）所示：

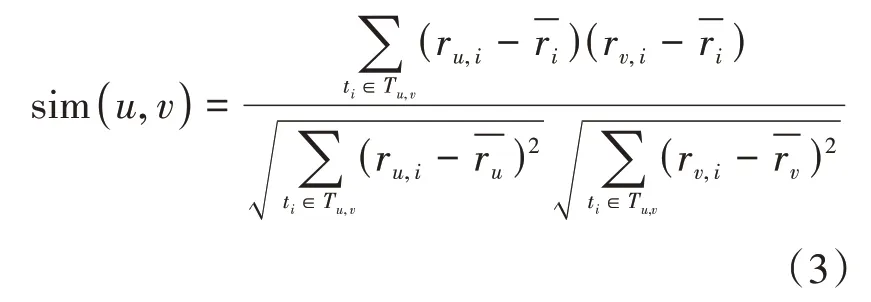
上述三个公式中，sim(u,v)表示用户u与用户v 之间的相似度；ru,i表示用户u对项目i的评分，rv,i表示用户v对项目i的评分；Tu,v表示用户u与用户v的共同评分项目集合；表示项目i的平均评分；表示用户u与用户v对所有存在评分的项目的评分均值。

2 本文改进算法

2.1 权重因子

在使用传统相似度计算方法时，首先需要找到用户之间的共同评分项目集合，其数量影响着相似度度量的准确性。比如，有3 个用户、5 个项目，他们对这5 个项目进行评分，评分尺度为10 分制度，具体评分如表1 所示，空白部分代表用户未进行评分。

表1 用户-项目评分表1

分别使用余弦相似度、修正余弦相似度、皮尔逊相关系数计算用户A 与用户B、用户C 之间的相似度，具体结果如表2所示。

表2 三种相似度计算方法得到的结果1

皮尔逊相关系数的计算结果表明，用户A与用户B更为相似。但并非如此，通过表1可以看出，用户A 与用户B 的共同评分项仅有两项，而用户A 与用户C 有四项，并且评分较为接近，所以用户A 应与用户C 更为相似，这是皮尔逊相关系数在计算相似度时不合理的地方。而余弦相似度在计算中结合了用户所有评分项目，修正余弦相似度在计算中结合了用户所有共同评分的评分均值，它们都考虑到了共同评分数量差异。因此，本文提出权重因子，将余弦相似度与修正余弦相似度相融合。具体公式如式（4）所示：

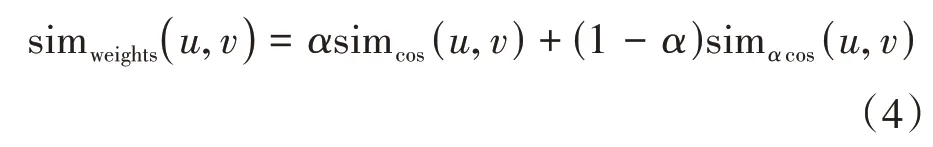
其中：

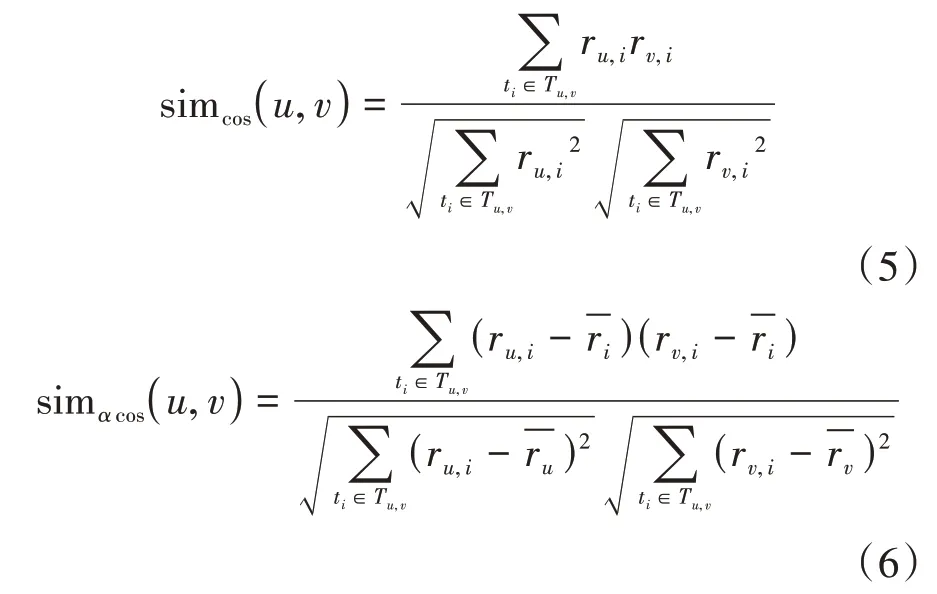
α的具体范围为（0，1），其具体数值根据后续实验结果进行选取。

2.2 修正因子

在实际中，用户喜欢某个项目的程度与其评分有关。但传统的计算方法考虑的是两个向量的趋势相关性，忽略了不同用户对相同项目的具体评分数值差异，导致结果缺乏准确性。

比如，有2 个用户、5 个项目，他们对这5个项目进行评分，评分尺度为10 分制度，具体评分如表3所示。

表3 用户-项目评分表2

根据上一小节，选取余弦相似度与修正余弦相似度分别计算用户A 与用户B 的相似度，具体结果如表4所示。

表4 不同相似度计算方法的结果2

根据表4 的结果，用户A 与用户B 的兴趣十分相似。通过表3中具体评分数值来看，虽然他们都对5个项目进行了评分，但他们对于每个项目的评分数值都有很大差异。比如项目1，用户B给出满分10分，而用户A只打了4分，这表明用户B 对项目1 很感兴趣，而用户A 对它不是特别的满意，所以二者的兴趣点有很大差异。

在使用余弦相似度与修正余弦相似度进行用户的相似度计算时，只考虑了用户的评分记录，忽略了用户的具体评分数值。因此，本文提出评分数值差异修正因子，具体公式如式（7）所示：

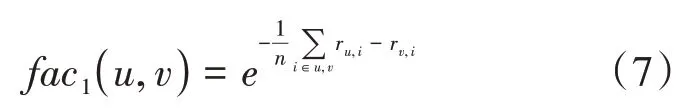
式中：fac1(u,v)表示衡量用户u与用户v之间具体评分数值差异的修正因子；ru,i表示用户u对项目i的评分，rv,i为用户v对项目i的评分；Tu,v为用户u与用户v的所有已评分项目中的共同该项目集合；n为用户u与用户v的共同评分项目集合的数量。当修正因子越小时，两个用户之间的评分数值差距越大。

传统的相似度计算方法对任何一个项目的权重值是一致的，这种方法不能完全体现出用户之间的相似性［13］，本文提出项目热门度差异的修正因子，具体公式如式（8）所示：

其中，fac2(i)为衡量项目i的热门度差异的修正因子；N(i)为对项目i有过评分记录的所有用户个数，即项目i的评分数量；all为用户-项目评分矩阵的所有用户数量。

2.3 时间衰减因子

用户的兴趣偏好会受到时间因素的影响［14］。在计算相似度时，将时间因素考虑至其中，捕捉用户的兴趣偏好的动态变化，从而提升相似度计算的准确性。本文提出时间衰减因子，函数如式（9）所示：

其中，λ=T0-1为衰减率，即为用户的兴趣偏好的衰减速度，在实际应用中，用户的兴趣偏好变化是通过调整λ的大小来实现的，若用户的兴趣偏好改变速度较快，则通过增大λ来适应。

2.4 最终改进的相似度计算方法

综合上述小节，将修正因子、时间衰减因子分别引入式（4）中，得到本文提出的新的用户相似度计算方法，如式（10）所示：

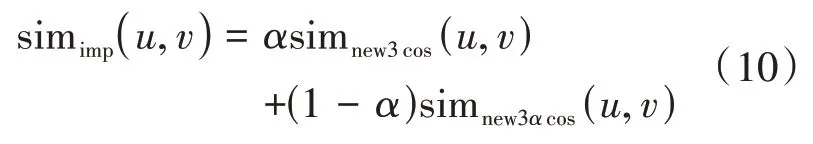
其中：

Tu,v表示用户u与用户v的共同评分项目集合；tu,i与tv,i分别表示用户u与用户v对项目i的评价时间。tu,v越小，两位用户对于同一个项目的评分时间就越接近，其相似性就越高。

3 仿真实验

3.1 所用数据集与评价指标

本文仿真实验采用MovieLens-1M 数据集［15］，它是6040 名用户对3952 部电影约一百万条评分数据，每名用户至少有20 个评分。本文通过交叉验证法进行实验，训练集选取其中80%的数据，测试集选取其中20%的数据。

实验对于算法的预测评分准确性所采用的评价标准为平均绝对误差MAE，如式（15）所示：

式中：Rtest表示测试集；Ru,i表示用户u对项目i的评分；表示用户u对项目i的预测评分。平均绝对误差值越小，说明算法的预测准确度越高。

算法的分类评分准确性所采用的评价标准为召回率Reacll，如式（16）所示：

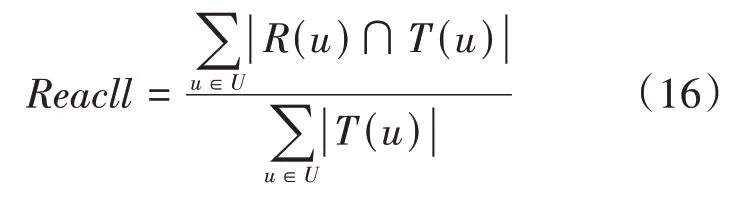
其中，R(u)为按照用户u在训练集上的行为预测出的推荐列表，T(u)为用户u在测试集上的实际的物品列表。值越高，说明算法的分类准确性越高。

3.2 实验流程

步骤1：根据数据集中用户历史行为信息构建用户-项目评分矩阵、用户-项目评分时间信息矩阵。

步骤2：计算目标用户的时间衰减因子、评分数值差异修正因子、每个项目的热门度差异的修正因子。

步骤3：通过改进的相似度计算方法计算目标用户与其他用户的评分相似度。

步骤4：将步骤3 中的评分相似度结果进行降序排列，将前N名用户集合作为该用户的最近邻集合。

步骤5：预测目标用户尚未进行评分的项目的评分。

步骤6：根据得到的评分预测结果计算MAE值。

3.3 实验结果及对比分析

3.3.1 实验一：相关参数确定

首先，选取最优的最近邻用户集合数量N，分别使用余弦相似度（COS）、修正余弦相似度（ACOS）、引入修正因子的余弦相似度（NEWCOS）、引入修正因子的修正余弦相似度（NEWACOS）的协同过滤算法在MovieLens-1M数据集上进行仿真对比实验，最近邻用户集数量N取值范围为［10，80］，步长为10。实验结果如图1所示。

图1 引入修正因子后的MAE值对比

由图1 可知，当N=30 时，NEWCOS 与NEWACOS 计算出的MAE值最小，因此在后续实验中N取30。继续使用NEWCOS 与NEWACOS 进行实验，λ的取值范围为［0.01，0.1］，步长设置为0.01，邻居数N取30，实验结果如图2所示。

通过图2，当λ=0.04 时，NEWCOS 与NEWA-COS 的的召回率Reacll值均达到最大。因此，选取λ=0.04 作为时间衰减因子，以达到最好的推荐效果。

图2 不同λ取值下的召回率

通过使用引入权重因子、修正因子、时间衰减的相似度计算方法的协同过滤算法（IMPCOS-CF）在数据集上进行实验，α 的取值范围为［0，1］，步长设置为0.1，邻居数N取30，时间衰减因子λ取0.04，实验结果如图3所示。

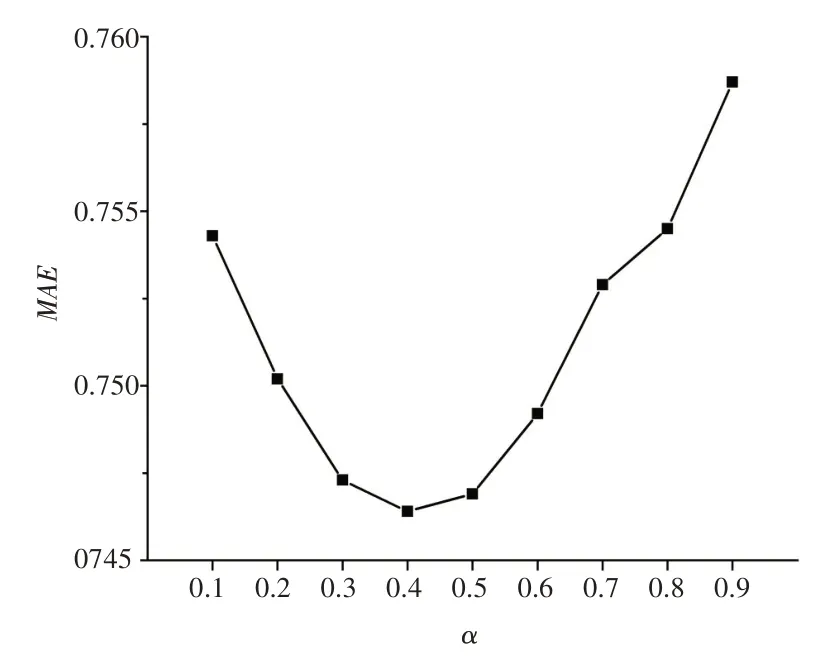
图3 不同α取值下的MAE值

由图3 可知，当α=0.4 时，MAE值最低，其中当α在［0.1，0.4］时，MAE值不断降低，之后随着α的不断增加，MAE值逐渐升高。因此当权重因子α=0.4时，基于IMPCOS-CF 得到的相似度度量的准确性最高，推荐算法的性能最优。

3.3.2 实验二：与其他算法对比

根据上述实验确定时间衰减因子、权重因子后，为了进一步验证本文所提出算法的性能，在本实验条件环境下将其与传统基于用户的协同过滤算法（User-CF）、基于袁正午［16］提出的基于多层次混合相似度的协同过滤推荐算法（LEVUser-CF）进行对比实验，实验结果如图4所示。

由图4可知，随着最近邻用户集合数量N的增加，三种算法的MAE值均呈现出减小并趋于稳定的趋势。不仅如此，IMPCOS-CF的MAE值低于其他两种算法。当N为30 时，IMPCOS-CF的MAE值达到最低；当N为50时，LEVUser-CF的MAE值略高于IMPCOS-CF算法。IMPCOS-CF相比User-CF，其MAE值平均降低了5.43%；相比于LEVUSer-CF，其MAE值平均降低了0.082%，说明本IMPCOS-CF 的用户评分预测准确性更高，算法的性能更强。

图4 不同算法的MAE值对比

4 结语

针对基于用户的协同过滤算法在相似度计算时的不足之处，本文引入权重因子、针对用户评分数值差异与项目热门度差异的修正因子、时间衰减因子对传统的余弦相似度与修正余弦相似度进行融合与改进；并在MovieLens 数据集上进行仿真实验，通过与传统协同过滤算法、其他改进的协同过滤算法进行对比，结果表明本文提出的IMPCOS-CF 算法能有效提高推荐算法的性能。