混合不完备数据的拓展高斯核-支持向量机分类方法

黄恒秋，翁世洲

（1.广西民族师范学院数理与电子信息工程学院，崇左 532200；2.广西民族师范学院经济管理学院，崇左 532200）

0 引言

支持向量机由Cortes 等［1］提出，是机器学习领域中非常重要的一种分类方法，它基于统计学习理论，具有结构风险最小化、鲁棒性强、泛化能力佳等优点［2］，已经在模式识别、信号处理、数据挖掘等诸多现实问题中得到广泛的应用［3-4］。

支持向量机训练本质上是求解一个二次规划问题［5］，对于小规模问题已有成熟的优化算法及软件工具可以使用，对于大规模问题也有诸如序列最小优化算法（SMO）［6］等优秀的研究成果，但是针对现实应用中广泛存在的混合不完备数据集则不能直接处理。所谓混合不完备数据集是指含分类型和连续型缺失属性值的数据集。目前，利用支持向量机处理该类数据集的方法主要有：①填充支持向量机分类方法。对缺失值进行填充处理后再进行分类，比如利用均值和主成分分析［7］、最近邻［7-8］、贝叶斯［8-9］、多项式回归［9］、期望最大化（EM）［10］、多层期望最大化和决策树［11］、粗糙集相容关系［12］、典型实例选择［13］、基于聚类的多重插值［14］等方法进行填充后再利用支持向量机进行分类。文献［11,15］还研究了将分类效果与填充方法相结合的选择-融合集成分类方法。②混合距离支持向量机分类方法。基于混合距离函数（Heteroge⁃neous Euclidean Overlap Metric，HEOM）［16］，用极端值代替缺失值后再进行分类，比如文献［17-20］。③风险重构支持向量机分类方法。对含有缺失值的对象，重新定义预测风险函数，通过最小化结构风险和预测风险，构建能处理缺失数据的支持向量机模型［21］。

基于填充的支持向量机分类方法，其研究成果最为丰富。然而，文献［22］指出，找到合适的填充方法，保证其分类效果，需要对不同的缺失类型、插值填充方法做多次交互操作才能实现。对于混合距离支持向量机分类方法，其关键在距离度量函数，正如文献［23］指出，HEOM距离将缺失属性值取作最大值或者最小值，如果属性较多且样本属性值缺失比例较大，会造成系统信息失真。这两种方法均需要对缺失数据进行填充处理，改变了数据集的原貌，其分类效果也不是原始数据集的真实反映。风险重构支持向量机分类方法则不需要对缺失数据进行填充处理，但是由于重构了风险目标函数及不完备对象的约束条件，增加了应用的复杂性。

为了避免对缺失数据进行填充或者取极端值而造成系统信息失真，同时又能充分度量不确定对象之间的相似性关系，文献［24-27］给出了同一度、对立度、差异度、势函数和集对距离的概念，文献［28］给出了邻域联系度距离函数的定义。本文首先基于文献［28］给出的邻域联系度距离函数，对高斯核进行拓展定义，使其能够直接处理混合不完备数据集；其次给出基于二次函数逼近的不确定高斯核支持向量机SMO训练算法和分类算法。

为了检验本文分类算法的有效性，取多个UCI 数据集进行了对比实验分析。首先，与决策树、单层期望最大化、多层期望最大化、选择-融合集成等经典插值填充支持向量机分类方法进行对比；其次与取极端值的混合距离支持向量机分类方法进行对比；最后，与文献［21］的风险重构支持向量机分类方法进行对比。实验结果显示，本文的分类方法获得了优异的分类效果。

1 支持向量机相关概念

1.1 支持向量机模型

对于两类问题，给定样本集(xt,yt)；xt∈Rn,yt=±1,t=1,2,…,l和核函数K(xt,xs)。K 对应特征空间的内积K(xt,xs)=(xt,xs)=(ϕ(xt),ϕ(xs))，ϕ为非线性函数。训练支持向量机分类器就是在特征空间中寻找使得两类间隔最大的超平面H。支持向量机的训练过程，本质上是解决以下二次规划问题：

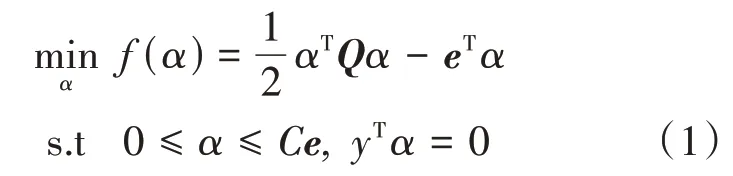
其中α为拉格朗日乘子，Q为Hessian 矩阵，Qts=ytysK(xt,xs)，e为全1 向量，C为惩罚因子。应用拉格朗日乘数法并满足KKT 条件：

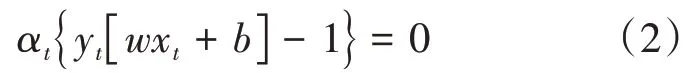
最后可得到上述最优化问题的最优分类函数：

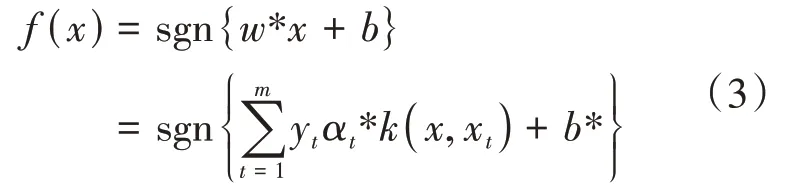
其中α∗为问题（1）的最优解，由（2）式知非支持向量=0，故

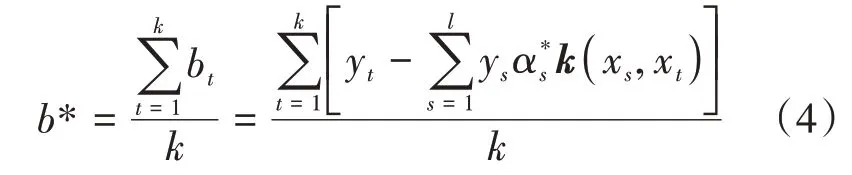
其中k为支持向量（α∗>0）的个数，即本文中最优分类超平面的偏置量b∗取支持超平面偏置量的平均值。

1.2 基于二次函数逼近的支持向量机SMO训练算法

训练支持向量机本质上是求解最优化问题（1），这是一个二次规划问题，变量个数与样本个数l相同，而矩阵Q的规模则是l×l。当样本个数较少的时候，利用目前成熟的二次规划问题求解方法即可。随着样本规模的增大，传统的二次规划问题求解方法不再适用，为了克服以上问题，不少研究者设计了基于分解的求解方法，文献［6］将分解方法推向极致，即每次只更新两个元素，称为序列最小化方法（SMO），文献［5］给出了二次函数逼近的SMO快速训练算法。

2 混合不完备数据的拓展高斯核-支持向量机分类方法

2.1 邻域联系度距离函数

定义1［20］混合距离函数（简称HEOM）定义如下：

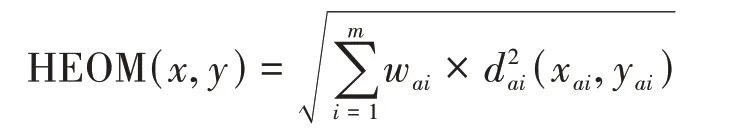
其中,

定义2［24］给定混合值不完备数据集I=(U,A∪D,V,f),|A|=N,Δ 为绝对值距离函数，（xi,xj）∈U2为集对。记ε为属性值相容的邻域半径，设M={a∈A|Δa(xi,xj)≤ε}为集对取值在相容邻域范围之内的属性集；H={a∈A|Δa(xi,xj)>ε}为集对取值在相容邻域范围之外的属性集；G={a∈A|f(xi,a)=∗∨f(xj,a)=∗}为集对取值不明确的属性集。记，则集对（xi,xj）的邻域联系度定义为

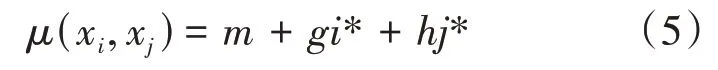
其中m,g,h记作同一度、差异度和对立度，i*、j*为差异度和对立度标记，起到与同一度区别的作用。

从定义1可以看出，HEOM 距离缺失值取极端值1代替，文献［29］则是以另一个极端值0 来代替。正如文献［23］所指出，当缺失值比例较大时这两种情况会造成系统信息失真。文献［24］从比较属性的相同部分、相异部分和不确定部分，即同一度、对立度、差异度三方面进行系统分析，且不需要对缺失值进行填充处理，不失为一种有效的不确定对象相似性度量方法。但是，如何将这种度量方法有效地应用于实际计算问题，阈值怎样设置等，文献没有给出进一步的讨论。从定义2可以看出，同一度反映了两个样本的相同或者相容部分，最理想情况为1。因此，将两个样本的同一度与最理想情况作比较，可获得其同一度的差异，而对立度和差异度，本身就反映了两个对象之间的差异。将它们的差异通过加权的方式计算出来，就是联系度距离。

定义3［28］给定样本x,y的邻域联系度μ(x,y)=m+gi*+hj*，则它们的邻域联系度距离定义为

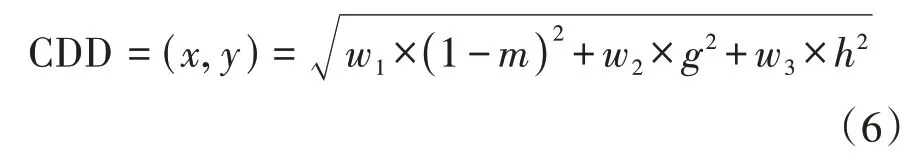
其中，w1,w2,w3为同一度、差异度和对立度的惩罚系数，且要求w1+w2+w3=1。

从定义可以看出，该距离函数继承了同一度、对立度和差异度在度量不确定样本相似性方面的优势，且利用的信息更加全面，同时避免了相关联系度阈值的选择问题，也避免了对缺失属性值人为干预填充或者取极端值的情形。

关于惩罚系数w1,w2,w3，事实上，两个样本属性取值不相同或者相异，最能反映样本之间的差异，体现为对立度，因此惩罚系数应该最大；差异度是由于样本属性值缺失造成的，缺失值有可能与比较样本相异，其惩罚系数次之；同一度，反映比较样本明确不相异部分，惩罚系数应该最小。

2.2 基于邻域联系度距离扩展高斯核函数的定义

高斯核函数是支持向量机分类问题中应用非常广泛的一类核函数。本文在传统的高斯核函数基础上，给出拓展定义的高斯核函数，用于对混合不完备数据进行处理。

定义4［5］高斯核函数定义如下：

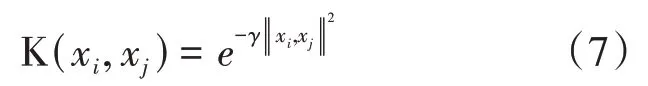
其中，γ为核函数宽度调整参数。从定义可以看出，高斯核函数是关于两个对象之间距离的函数，其距离为确定距离。下面将给出基于不确定距离——联系度距离的不确定高斯核函数定义。

定义5基于邻域联系度距离拓展定义的高斯核函数如下：

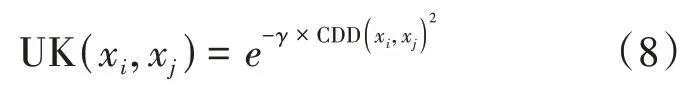
其中，γ 的含义同定义4，而CDD(xi，xj)则为对象xi,xj的联系度距离。

2.3 基于二次函数逼近的拓展高斯核-支持向量机SMO训练算法

算法3 没有改变二次规划问题（1）的模型结构和约束条件，还充分利用了文献［5，6］SMO训练算法的研究成果，本质上没有增加求解的复杂性，从而更好地推广应用到实际问题当中。

2.4 混合不完备数据的拓展高斯核-支持向量机分类方法

传统支持向量机模型是基于二分类问题，而实际应用中的数据集不仅包括二类，还可能存在多类。下面给出多类（包括二类）混合不完备数据集的支持向量机分类算法。

3 实验分析

从http://archive.ics.uci.edu/ml/下载6 个UCI数据集，其中iris、pima-indians-diabetes（下表用pima表示）、wine为完备数据集，其他数据集为不完备数据集，具体信息见表1。

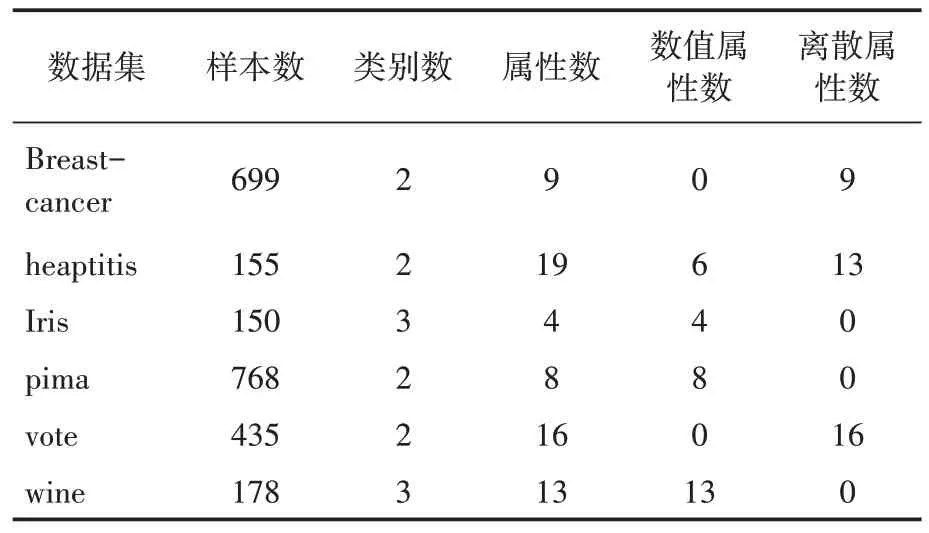
表1 实验数据集基本信息表

实验采用MATLAB2011b 进行编程，数值属性值采用极差法全部规范化为［0，1］之间。取支持向量机模型中的惩罚系数C=1，不确定高斯核函数宽度调整参数r=1/N，其中N为数据集的属性个数。联系度距离中的惩罚系数，根据2.2的分析，取w1=0.1，w2=0.2，w3=0.7。关于相容邻域半径ε的选择，不同数据集，其属性取值相容程度是不同的，但是由于数值属性都规范化到［0，1］之间，因此取ε介于［0.05，0.3］（间隔0.05），并通过实验从中选择最优分类精度对应的ε，即为该数据集最佳相容邻域半径。

下面分别讨论本文的分类方法（ISVM）与填充支持向量机分类方法、混合距离支持向量机分类方法、风险重构支持向量机分类方法的对比实验分析。

（1）ISVM 与填充支持向量机分类方法对比实验分析。选择与文献［11］相一致的数据集Breast-cancer、vote、pima 进行对比实验分析。对每个数据集依次随机增加0%（原始数据集）、10%、20%、30%的缺失比例，利用ISVM 进行分类，以6次交叉检验获得的平均精度作为分类精度。为了保证结果的稳定性，重复以上实验5 次，取其平均值作为最终的分类精度，并与文献［11］基于决策树、单层期望最大化、多层期望最大化、基于随机投票的选择-融合集成、基于CVI 的选择-融合集成的填充支持向量机分类方法获得的分类精度（依次记为TJD1、TJD2、TJD3、TJD4 和TJD5）进行对比。实验对比结果如表2所示。

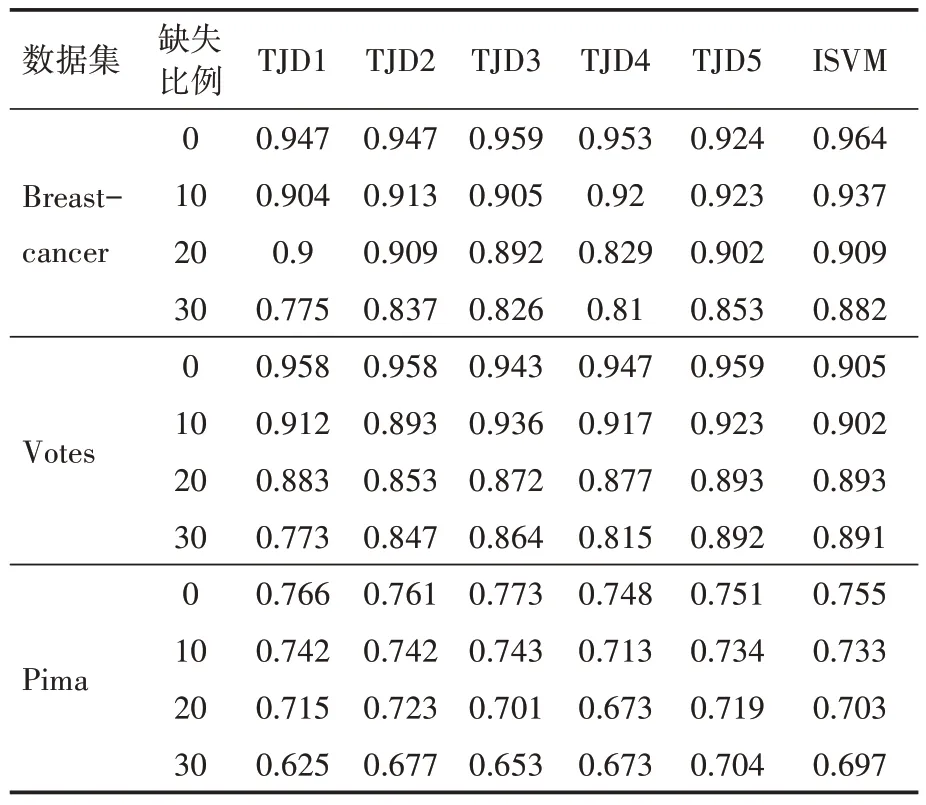
表2 ISVM与填充支持向量机分类方法对比实验

从表2 结果可以看出，Breast-cancer 数据集缺失比例从0%增加到30%，ISVM 均获得了最佳的分类精度。Votes 数据集的缺失比例从0%增加到10%，ISVM 分类精度稍差，但是正确率也在90%以上；缺失比例从20%增加到30%，其优势则明显体现出来。Pima 数据集在缺失比例从0%增加到20%时，ISVM 与填充支持向量机分类方法的分类效果差别不大，而缺失比例增加到30%时，ISVM的优势也体现出来。

（2）ISVM 与混合距离支持向量机分类方法对比实验分析。选择表2 中的6 个数据集进行实验分析，对每个数据集依次随机增加0%（原始数据集）、10%、20%、30% 的缺失比例，利用ISVM 与缺失值取属性最小值0 和最大值1 的混合距离支持向量机分类方法进行分类，以6次交叉检验获得的平均精度作为分类精度。为了保证结果的稳定性，重复以上实验5 次，取其平均值作为最终的分类精度进行比较。具体对比结果见图1，其中横轴表示缺失比例，纵轴表示分类精度，星号连线表示ISVM 获得的结果，三角形和圆圈连线分别表示缺失值取属性最小值0和最大值1的混合距离支持向量机分类方法。

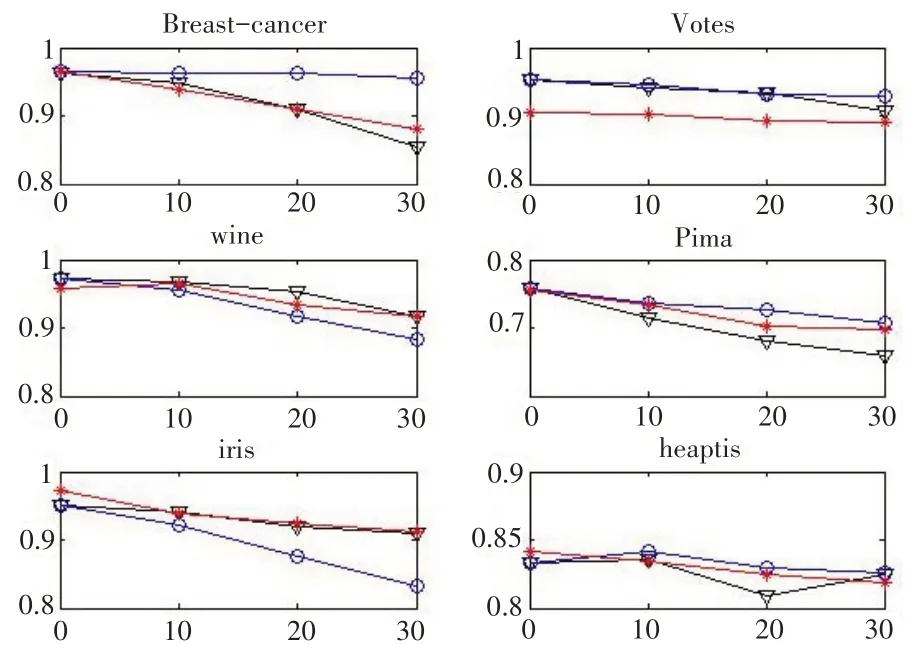
图1 ISVM与混合距离支持向量机分类方法对比实验

从图1 可以看出，实验的6 个数据集在缺失比例从0%增加到30%过程中，ISVM 与取极端值的混合距离支持向量机分类效果总体上差别不大，也均保持在相对较高的分类精度。

（3）ISVM 与风险重构支持向量机分类方法对比实验分析。文献［21］选择了一个公共测试数据集heaptitis，对经典的SVM、CSVM、LS-SVM、CLS-SVM 进行风险重构，并进行分类。利用ISVM 进行分类，以10次交叉检验获得的平均分类精度作为比较，具体对比结果见图2，其中横轴方法1-5 依次对应SVM、CSVM、LS-SVM、CLS-SVM风险重构方法和ISVM。

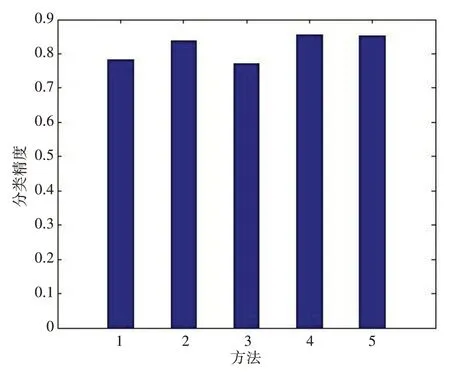
图2 ISVM与风险重构支持向量机分类方法对比实验

从图2 可以看出，ISVM 对比风险重构支持向量机分类方法，具有显著的优势。

综上可以看出，本文的分类方法是有效的，而且对比填充支持向量机分类方法、混合距离支持向量机分类方法和风险重构支持向量机分类方法，均获得了优异的分类效果。值得说明的是，本文的分类方法没有对缺失值做任何填充处理，也没有取极端值或特殊值进行代替，完全保证了分类数据集的客观真实性，其分类效果也是真实数据集的反映。同时，本文的分类方法没有改变经典支持向量机模型的结构和约束条件，可以充分利用现有的支持向量机研究成果，从而避免了增加应用的复杂性。

4 结语

本文针对混合不完备数据集，首先给出基于邻域联系度距离拓展定义的高斯核函数；其次，给出基于二次函数逼近的支持向量机SMO训练算法和分类算法；最后，取多个UCI 数据集进行了实验分析。通过与填充支持向量机分类方法、取极端值的混合距离支持向量机分类方法和风险重构支持向量机分类方法获得的分类精度进行比较，实验结果显示本文分类方法均获得了优异的分类效果。值得说明的是，本文的分类算法不需要对缺失值做任何填充处理，也不需要取极端值或特殊值进行代替，完全保证了分类数据集的客观真实性，而且没有改变经典支持向量机的模型结构和约束条件，避免了增加应用的复杂性，这是对比的分类方法所不具备的优势。将邻域联系度距离函数应用于更多的核函数与分类、聚类模型，以更好地对不完备数据进行处理、研究及应用，将是我们下一步的主要研究工作。