基于时间注意力图卷积的民航旅客需求预测
2022-02-03俞嘉慧吴薇薇陈嘉鑫
俞嘉慧 ,吴薇薇 ,刘 鹏 ,陈嘉鑫
(1.南京航空航天大学 民航学院,南京 211106;2.上海吉祥航空股份有限公司,上海 200335)
近年来,随着人们出行需求的进一步增加,民航市场规模整体呈现快速增长的趋势,其对于社会经济的影响作用也日益凸显,因此合理规划航空运输活动、有效分配资源设施,成为提升经济效益的重要措施之一.在航空运输规划活动中,明确旅客运输需求成为解决问题的关键所在,但由于民航客运需求存在较大的不确定与时空动态性[1],在研究中如何基于时间与空间多维影响因素实现有效预测存在一定难度,这也是本研究的重要着力点.
纵观国内外学者的现有研究,对于民航领域内的需求预测,前期多采用传统模型、数据特征与影响因素相结合的预测方法,且研究对象主要集中于客运量等相关数据.Jing 等[2]、Zhao 等[3]基于ARIMA方法,构建预测模型,有效捕捉数据间的线性关系,但较难适用于波动性较大的数据;蔡文婷等[4]、李维等[5]考虑多个影响因素,基于回归模型,有效提升预测精度;任新惠等[6]、沈静瑶等[7]区别于传统方法,基于系统动力学模型与各影响因素的因果关系进行预测研究.
随着人工智能的高速发展,Vlahogianni 等[8-9]在研究中指出,预测研究已从传统的预测方法逐步转入机器学习,且人工神经网络作为机器学习中具有代表性的模块,已在预测领域取得众多成功.在民航需求预测方面,常用的神经网络主要包括卷积神经网络(Convolution Neural Network,CNN)与循环神经网络(Recurrent Neural Network,RNN)两大模块.Cho 等[10]在RNN 基础上,首次提出结构简单的门控循环网络模型(Gate Recurrent Unit,GRU);Rui 等[11]后续将其应用于流量预测,并取得有效的预测结果;孙卫卫[12]在横向与纵向时序方面建立预测模型,利用循环神经网络,实现了航班日订座数的有效预测;康友隐[13]以航班用户查询量作为需求指标构建时间序列,提出了基于卷积神经网络的DSTRN-FRP 预测模型;林友芳等[1]在民航需求预测中搜集区域间的客运量数据,考虑序列中时间与空间的依赖关系,基于循环神经网络建立STLSTM-PDP 模型.
由于实际预测问题涉及较为复杂的图网络结构,Bruna 等[14]在研究中提出基于频域和基于空间域的两种图神经网络,以捕捉不规则拓扑图中的结构关系;Kpif 等[15]首次将卷积网络应用于图数据,构建图卷积神经网络(Graph Convolution Neural Network,GCN),为后续学者[16-17]提供更为完善的基础模型.在基于图卷积网络的预测研究中,陈喜群等[18]在短时交通流预测中以图卷积为基础,构建包含路网拓扑结构与流量数据时空相关性的预测模型,有效提高了预测精度;Zhao 等[19]结合图卷积与门控循环网络构建预测模型,在图数据规则化的同时,有效获取时空特性;Yu 等[20]将交通流转化为图问题,基于图卷积模型,构建考虑时空特征的时空图卷积模型;Zheng 等[21]基于交通系统的时空因素,在图结构的基础上,引入注意力机制,进一步提升预测性能;Guo 等[22-23]在研究中基于图神经、图卷积网络与注意力机制,构建ASTGCN 与ASTGNN 预测模型,捕捉交通数据的时空动态特征与全局信息,有效地解决地面交通流量等预测问题;Song 等[24]基于数据时空特性,构建时空同步图卷积网络,有效地捕获复杂的局部时空相关性,并在地面交通流预测方面取得有效结果.基于图卷积的预测研究能够更好地提取网络结构的空间特征,但目前大多用于地面交通问题,对于解决民航相关问题的应用较少,且涉及中转航线的预测研究更是鲜有.
从研究现状来看,基于图卷积的预测方法在研究网络结构的空间特征方面具有显著优势,循环神经网络与注意力机制能够进一步捕获时间序列的周期变动特征,但目前基于图卷积与注意力机制的预测方法在民航需求预测领域的应用较少,现有研究指标也较为宏观,大多从月度、年度客运量角度开展,鲜有能精确到不同航线、具体单天时间。因此,本文作者以中转航线网络为研究对象,将GCN、Attention 机制引入其中以实现更为精细的需求预测研究。从反映旅客需求的时间序列出发,在利用GCN获取空间特征的基础上,进一步获取需求序列的时间特征构建时间注意力图卷积神经网络(Attention Temporal Graph Convolutional Network,ATTGCN)预测模型,更为全面考虑需求序列前后时段的影响特征,实现图卷积、注意力机制与循环神经网络的融合应用。
1 问题描述
对于航线网络中的旅客需求进行研究,选取不同出发地-目的地的旅客运输量进行预测,即可实现不同起讫点(Origin-Destination,OD)的客流预测.传统航线网络,指以机场为节点、以机场和机场之间的连线为边、任意两个机场按照一定方式连接而成的系统,如图1(a)所示;本文区别于传统航线网络,以OD 为节点、以OD 与OD 间的中转机场为边构建网络体系,如图1(b)所示,以此分析不同需求下的时间空间分布特点.

图1 航线网络结构的表示方式Fig.1 Representation of the route network structure
基于不同的OD 特性,研究其存在的拓扑结构关系,在无权图G=(V,E)的基础上,定义第t时间段的航线网络的有权图结构为G=(Vt,E,W).其中,Vt为网络图中节点的集合,对应于各个OD 的旅客运输量;E表示边的集合,对应于各个OD 间的连接关系,在此网络中对OD 间的中转点进行具象表示,如图1(b)所示,当BA与AC两个OD 间存在中转机场A时,其相互间的连接关系可由中转点A来表示;W表示图结构中的加权邻接矩阵,代表不同节点间影响关系的权重系数.林友芳等[1]在研究中指出,不同OD 间客运需求的空间影响关系可通过需求序列的关联性进行分析,因此本文中的W以存在中转点时,相邻OD 的客运量相关系数进行具象表示如下

考虑不同航线的旅客需求特性与前后航线间的影响关系,基于航空公司的中转航线构建小型网络,并选取航线中各条OD 的旅客运输量为观测对象,在阐述航线网络与基础特征的前提下,将旅客需求预测问题进行转化,以求解最终的预测结果,有

式中:Xt∈Rn×n表示在t时间段的n条航线的相关向量,向量中各个元素的数值为对应航线的具体数值.
式(2)表示由 前n个需求 观测值Xt-n,…,Xt-1,Xt,结合网络图结构中的拓扑关系,预测下一个步长为T时间段内的需求值Xt-n,…,Xt-1,Xt.
2 旅客需求预测模型构建
2.1 时间注意力图卷积模型构建
在现有理论的基础上,本文从航线网络角度,捕捉旅客需求的时间特征与空间特征,构建基于图卷积神经网络、门控循环神经网络与注意力机制的时间注意力图卷积预测模型,以实现时空特征的有效融合.此模型一方面利用图卷积获取航线网络中航线间的拓扑结构,另一方面利用门控循环神经网络与注意力机制获取旅客需求序列的前后特征,具体如图2 所示.
时间注意力图卷积模型主要由多个TGCN 单元、注意力模块与全连接输出层构成,图2 左侧部分反映时间图卷积模块的具体流程,t时刻的输入数据与前序训练单元的输出信息共同作用,输出各时段特征信息;图2 中间部分反映注意力作用模块,不同时段的特性信息通过多层感知器映射,最终得到全局时段特征;图2 右侧部分反映模型最终的预测结果.
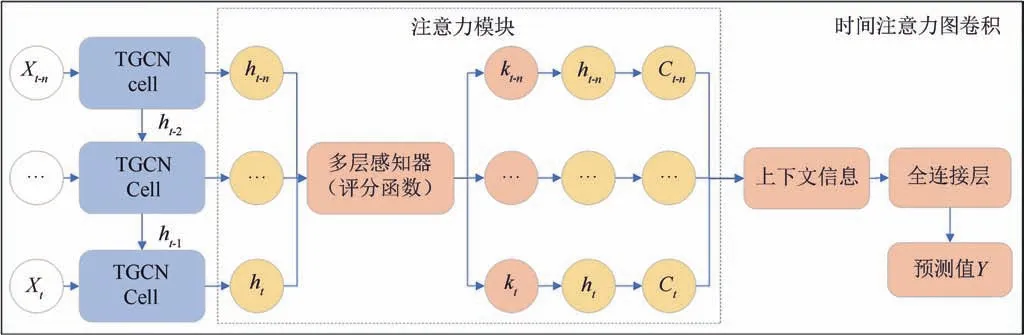
图2 时间注意力图卷积的内部结构Fig.2 Attention temporal graph convolutional network internal structure
模型在预测过程中,首先依据时间预测步长与网络节点个数,将反映旅客需求的二维特征矩阵X转化为三维张量,通过获取空间特征的GCN 模块进行图数据的规则化操作与卷积运算,且单元中的图卷积变换层数设置为2;其次将接收到的空间、时间信息输入GRU 模块,以此获取各个单元间的动态信息变化;紧接着将各时段状态特征输入到注意力模型,以确定全局时段特征;最终依据全连接层获得规格为二维张量的预测结果Xt+n,即实现式(2)所述的需求预测.
2.2 基于谱图信息的图卷积模块
图卷积神经网络的本质在于能够提取网络中的空间结构,捕获网络图中的节点信息.第1 节提出的航线网络结构属于拓扑图结构,网络中的各条航线以节点的形式通过拓扑结构呈现出来,其中不仅包含节点自身需求特征,还囊括节点间的关系特征,可通过图的邻接矩阵进行表述,但此时用于处理规则数据的卷积神经网络有一定的局限性.而图卷积神经网络能够弥补这一缺陷,从空间角度聚集与转换中心节点的领域信息,实现不规则图数据的规则转化.图卷积在处理数据过程中,需要表述节点相互关系的邻接矩阵A与反映节点特征的矩阵X,内部隐藏层的变化过程如下
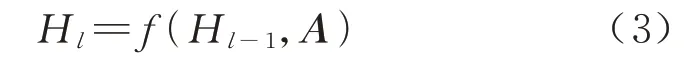
式中:Hl为第l层的激活值;H0为航线网络中的特征矩阵X;f为传播规则.其数据在传播过程中的具体规则如下
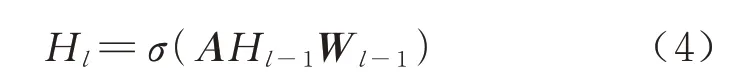
式中:Wl-1为各层中的权重矩阵;σ为非线性激活函数公式.
在图卷积分层传播与变换规则的基础上构建GCN 模块,叠加多个卷积层,以获取航线网络中节点间的空间信息,其变换通式如下

2.3 基于时间特征的门控循环模块
由于门控循环神经网络能够捕捉时间序列前后特征,在预测时间序列方面具有显著的优势,因此采用门控循环网络捕捉航线网络中的旅客需求特征,其内部结构如图3 所示.门控循环神经网络中存在多个门控单元,其单元中的重置门rt与更新门ut用于获取时间序列具有的前后特征,ct用于存储t时刻的信息数据,Xt用于表示数据的输入状态,ht用于表示t时刻的输出状态,σ与tanh 均为激活函数.
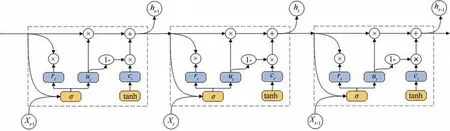
图3 门控循环神经网络内部结构Fig.3 Gated recurrent neural network internal structure
对于航线网络中的各个节点,门控循环网络对输入的航线客运量数据进行特征挖掘,在激活函数与权重矩阵的共同作用下,实现信息的更新与重置,具体变换如下
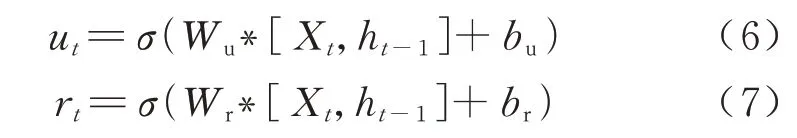
式中:Wu与Wr分别为门控循环单元中更新门与重置门的权重信息;σ表示为激活函数sigmoidbu与br分别为门控循环单元中更新门与重置门的偏移信息.
与此同时,ct依据式(8)与重置门共同作用,实现对前序门控循环单元输出信息的存储.

式中:Wc为存储模块的权重信息;bc为存储模块偏移量.
通过式(9)的变换获得航线网络t时刻的输出数据,依次传递给后续门控循环单元.
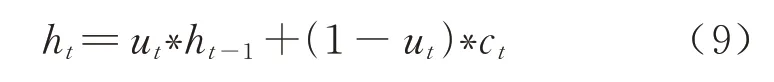
基于时间特征的门控循环神经网络模块,有效获取航线网络中旅客需求的前序与周期特征,具备优秀的记忆功能.
2.4 融合时空特征的时间图卷积模块
时间图卷积单元(TGCN Cell)的主要结构如图4 所示.旅客需求数据Xt首先通过获取空间特征的GCN 模块,进行图数据的规则化操作与卷积运算;其次将接收到的空间、时间信息输入GRU 模块,以此获取各个单元间的动态信息变化.在此过程中,单元能够在规则数据的基础上更好地捕获时间特征,对于考虑航线需求的周期变动具有较优的应用意义.时间图卷积的整体内部结构的变换公式与上述门控循环模块具有一定的相似性,具体如下:

图4 时间图卷积内部结构Fig.4 Temporal graph convolutional network internal structure

式中:GC 表示图卷积过程中的输出结构;W和b可表示训练过程中的权重和偏差.
式(10)~式(13)与式(6)~式(9)具有相似功能,可对输入需求信息进行更新、重置、储存等多项记忆操作.
2.5 基于全局特征的注意力模块
不同航线的运输量作为反映旅客运输的需求指标,其数据曲线的波动包含着需求动态变化与时间影响特征,且不同时间节点对后续需求的影响程度不尽相同,具有相应的周期变动规律.为更好地获取不同时间节点的重要性指标,在模型中引入注意力机制,在时间图卷积获取特征的前提下,基于评分函数,计算得出不同时间节点下状态特征的综合得分,获取全局视角下需求变动规律,最终实现更为精准的有效预测,有

式(14)为评分函数,其中H为不同时间节点下的特征集合,w1、b1与w2、b2分别 为第一层、第二层的权重与偏差,输入值为各个时间下的特征hi,输出评分可通过两层隐藏层获得;式(15)代表各个时间点特征的权重占比;式(16)代表权重划分下的全局特征信息.
在时间注意力图卷积模型的训练与测试中,为判断模型的运行性能,需设置相应的损失函数.在构建AT-TGCN 模型时,采用L2 正则化损失函数进行效能评估.在训练过程中不断迭代,使得损失函数达到最小值,以此确定模型内部所需的各项参数,有
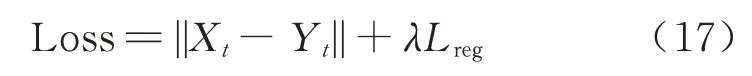
式中:Xt和Yt分别表示实际旅客需求与预测需求.
3 基于时空特性的旅客需求预测应用
本文以2017—2019 年我国航空公司的相关运行数据构建航线网络,并对旅客需求进行预测研究,验证AT-TGCN 模型在航线需求方面具有的预测优势.
3.1 航线网络构建
由于疫情的影响,去除了2020 年的相关数据,选取某航空公司2017—2019 年历史航班运行数据作为研究对象,将不同的OD 作为图结构中的节点,以OD 间的中转点作为边构建航线网络.由于在研究中需要考虑航线需求间的空间影响关系,因此预测研究主要针对航空公司的中转航线展开,从航空公司39 万余条航班信息中整理得出59 420 条存在中转点的航班信息,同时为保证所研究航线的稳定性,筛选得出该航司3 年中执飞天数大于总天数80%的9 条中转航线,其中包括:大连—南京—张家界(DLC-NKG-DYG)、张家界—南京—大连(DYG-NKG-DLC)、银川—上海—关西(INCPVG-KIX)、昆明—毕节—上海(KMG-BFJ-SHA)、关西—上海—银川(KIX-PVG-INC)、丽江—长沙—上海(LJG-CSX-PVG)、丽江—贵阳—杭州(LJGKWE-HGH)、上海—毕节—昆明(SHA-BFJKMG)、厦门—上海—名古屋(XMN-PVG-NGO),并将9 条中转航线转化为18 条OD,构建中转航线为主的小型航线网络,具体如图5(a)所示.
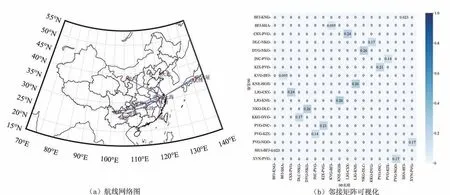
图5 航线网络时空特性的构建Fig.5 Construction of temporal and spatial characteristics of airline network
图5(b)为航线网络中邻接矩阵的可视化表达,图中右侧蓝色渐变色带说明邻接矩阵中各个节点间的影响关系权重处于[0,1],颜色越深代表权重系数越大,两点之间的需求影响关系越密切.
3.2 数据采集
为体现图卷积中的层级结构,充分把握OD 间存在的影响关系,应尽可能使具有中转关系的OD存在相邻的时间切片中.根据航班信息统计显示,以3 h 为间隔的情况下有82%的中转航班处于相邻时间片,因此依据各航班离港时间,以3 h 为间隔进行各OD 旅客运输量的数据采集,具体如表1 所示.同时,由于航班执飞时刻在1、2 时段的数量较少,因此仅针对3~8 时段,即06∶00—23∶59 进行航班信息统计.
表1 时段的划分Tab.1 Time division
3.3 数据预处理
由于汇总得出的航线数据存在部分数据缺失与异常值的情况,需要对数据进行清洗与处理,排除无效数据对预测的干扰.对缺失的数据进行线性插值予以补全,有

对于不正常的数据,依据同期的旅客运输情况进行有效替换,同时由于部分OD 存在连续时段中客运量为0 的情况,最终选取2017 年3 月27 日—2019 年12 月30 日间的客运量数据进行研究.
3.4 实例预测
3.4.1 预测环境与参数
针对现有理论与数据基础,本实验在Python3.6的软件环境下运行,模型的构建使用了Python 中的深度学习框架Tensorflow1.14.0.在预测应用中,选取2017 年3 月27 日—2019 年12 月30 日中前80%的需求数据为训练集(即2017 年3 月—2019 年5 月的相关数据),剩余20%的数据为测试集,在测试与训练集中均将历史时间窗口设为6 个时间段(即表1中所划分的各个时段),分别预测未来1、2 个时间段的旅客需求数据.在模型参数的设置中,初始学习率设为0.001,数据批量大小设为64,隐藏单元设为32,训练周期设为3 000,并在优化过程中使用了Adam 优化器进行训练.
3.4.2 评价指标的选取
为对时间注意力图卷积预测模型进行误差与可行性的分析,本文选用4 个常用度量指标进行性能评价,分别为均方根误差(Root Mean Square Error,RMSE)、精确度(Accuracy)、确定系数(RSquared,R2)、可释方差(VAR),具体计算公式如下

式中:为需求预测值;Yt为真实数值;n为序列的时间长度.
在所选择的评价指标中,RMSE 被用来衡量预测误差的大小,其数值越小,方法越具有优越性;Accuracy、R2与VAR 分别用来表示所用方法的精确程度与预测结果相关性,数值越接近1,代表预测模型的可信程度越高.
3.5 预测结果分析
3.5.1 不同模型的预测结果比对
为验证AT-TGCN 模型在此预测问题中所具有的有效性与准确性,本文将AT-TGCN 模型的预测性能指标与其他基准模型的相关指标进行对比分析,所选的对比基准模型主要包括HA(历史平均)、ARIMA(自回归综合移动平均)、SVR(支持向量回归)、GCN[15](图卷积神经网络)、GRU[10](门控循环神经网络)与STGCN[20](时空图卷积)等.其中,HA为历史平均模型,此模型依据历史范围内旅客运输量数据的平均值进行预测研究;ARIMA 为自回归综合移动平均模型,将所需研究的不平稳时间序列输入模型进行差分处理,最终对差分得出的平稳序列进行预测;SVR 为支持向量机回归模型,将时间序列输入预测模型,在核函数为Linear 的情况下得到最优预测结果;GCN 与GRU 分别为前述的图卷积神经网络与门控循环神经网络;STGCN 为时空图卷积预测模型,能够基于完整的卷积结构获取数据的时空特征.
不同模型的预测结果如表2 所示,这些均在相同数据、训练参数等基础上进行.从表2 中的数据结果可知,不论是在预测时间窗口为1 个时间段还是在2 个时间段(划分依据详见表1)的情况下,AT-TGCN 模型下的性能指标均表现为最优状态.对于处理多项复杂的、不平稳的时间序列,HA、ARIMA 模型具 有一定 的局限 性;SVR、GCN 与GRU 模型由于缺少时间或者空间特征的多重捕捉,其预测效果较AT-TGCN 模型仍有一定的差距;STGCN 在预测过程中考虑了数据的时空特性,在相同数据集的测试环境下,虽在1 时段预测下显示出较优的预测性能,但在2 时段情况下与AT-TGCN 的差距较为明显,此时对数据集的要求更为严格,因此对于中转网络的预测研究有一定的局限性.

表2 AT-TGCN 模型与其他基准模型在需求数据集上的预测结果Tab.2 The prediction results of AT-TGCN model and other reference models on the requirements dataset
在预测窗口为1 个时段的情况下,GRU、GCN、STGCN、AT-TGCN 的预测曲线与真实值的比较结果如图6 所示.其中横坐标为测试天数中依据表1划分的多个前后时间段,代表不同日期下的不同时间,共有1 199 个连续时段;纵坐标为旅客运输人数.可以看出,AT-TGCN 的预测结果更接近真实值,说明该模型能够更好地捕捉航线需求的时间与空间特征来进行预测研究.

图6 不同模型的预测曲线Fig.6 Prediction results of different methods
3.5.2 预测结果分析
1)AT-TGCN 较其他模型的预测性能优势.
较传统模型,AT-TGCN 的预测优势在于考虑了航线网络中的空间特点,即在传统GRU 模型中加入了GCN 模块,所以能更好地挖掘航线网络图中的拓扑结构关系,获取数据存在的时空关系,因此具有较强的预测性能优势.如表2 所示,不论是在预测窗口为1 个时段还是在2 个时段的情况下,AT-TGCN模型下的性能指标均表现出最优状态.这里选取预测窗口为1 个时段下多种方法的预测结果进行具体分析.如图7(a)所示,从模型预测误差即RMSE 评价指标来看,AT-TGCN 模型的预测结果较HA 模型降低了54.99%,较ARIMA 模型降低了61.33%,较GCN 模型降低了25.42%,较SVR 模型降低了17.90%,较GRU 模型降低了21%,较STGCN 模型降低了3%;如图7(b)所示,从模型预测精度与可靠性(即Accuracy、R2与VAR 评价指标,此处选取Accuracy)来看,AT-TGCN 模型的预测准确性较HA模型提升了8.06%,较ARIMA 模型提升了11.93%,较GCN 模型提升了2.22%,较SVR 模型提升了1.31%,较GRU 模型提升了1.63%,较STGCN 模型提升了0.42%,具有一定的预测可靠性.

图7 多时段下不同方法的预测结果Fig.7 Prediction results of different methods
2)AT-TGCN 针对不同OD 的预测结果对比.
在预测结果过程中,针对不同的航线,ATTGCN 的预测结果也存在一定的差别,在预测窗口均为1 个时段的情况下,选取多条OD 进行预测结果的比对分析,具体如图8 所示.

图8 不同OD 的预测结果Fig.8 Prediction results of different ODs
BFJ-SHA 与LJG-KWE 的数据波动具有明显的周期规律且变化较为平稳,而DLC-NKG 与KIXPVG 的数据波动较为杂乱,时间规律有所欠缺,在此情况下,前者的预测精度明显优于后者的预测精度,因此认为AT-TGCN 模型对具有规律周期变化的时间序列能够发挥更好的预测性能,能有效获取时间波动特征.
3)AT-TGCN 基于多时段窗口下的预测能力.
在实验过程中,AT-TGCN 模型可选择不同的时段窗口进行预测.预测结果显示,AT-TGCN 在预测窗口为1 个时段和2 个时段这两种情况下,与其他模型相比,所取得的结果均为最优.本文以BFJ-SHA 与XMN-PVG 为例,针对相同OD、不同预测窗口的预测结果进行对比分析,如图9 所示,结果表明:由于旅客需求时间序列的前后影响关系多集中于相邻时间段,且随着时间推移逐步递减,预测窗口为1 个时段的精度均优于2 个时段的结果,且其预测精度误差多集中于峰值阶段,因此该方法能够更好地适用于平稳的短时需求预测研究.
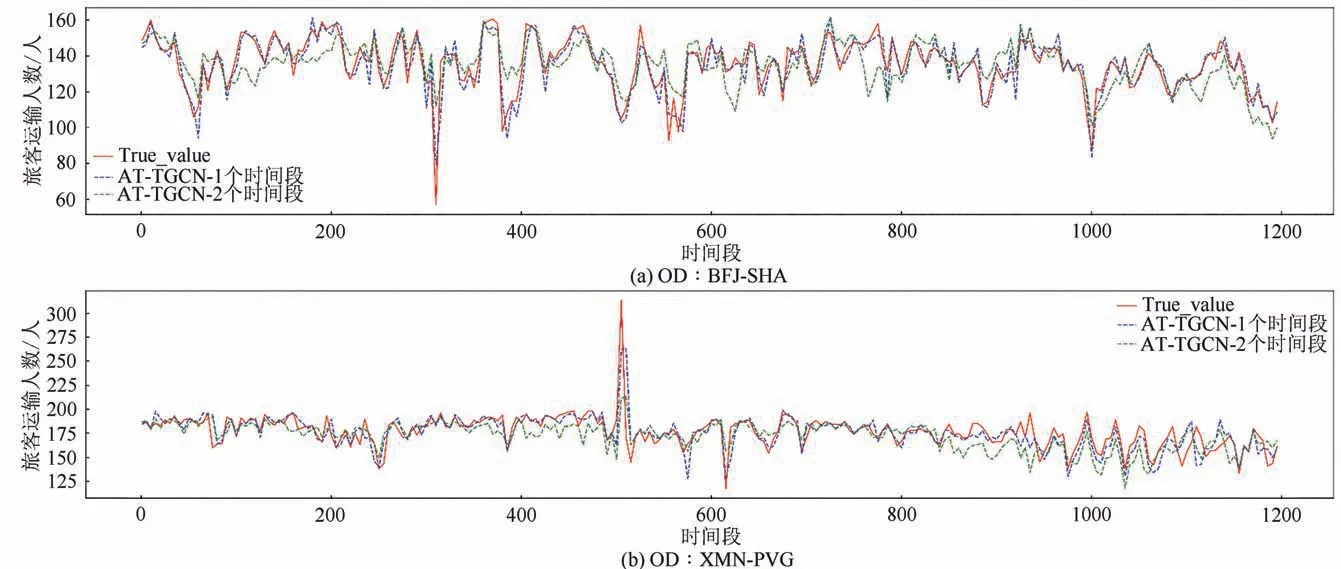
图9 不同预测窗口下的预测结果Fig.9 Prediction results of different time
综上所述,AT-TGCN 模型区别于传统的链式预测,考虑了航线网络图的拓扑结构特点,有效捕捉了多条OD 需求的空间影响关系与需求序列本身的前后周期变动,在实际应用中具有较高的预测精度,为航空公司了解中转旅客的需求变化、解决中转实际问题提供了有应用价值的预测模型.
4 结论
1)AT-TGCN 模型在传统时空模型的基础上引入图卷积与注意力模块,能够更好地获取不规则图数据的空间特征与全局时间特征,把握中转航线前后时段的需求影响关系,相较于传统预测模型具有明显优势.
2)以OD 间的中转点作为影响不同航线旅客需求的空间影响因素,以相关性系数作为影响权重,实现了中转航线网络中的旅客需求间空间影响关系的可视化分析.
3)预测结果显示,考虑空间特征的AT-TGCN模型在中转航线网络的旅客需求预测方面存在显著优势,尤其在短时预测方面更为突出,且针对具有周期变动的时间序列能够更好地把握全局特征,为后续航空公司准确了解中转旅客需求的周期波动提供了有应用价值的预测模型,具有重要的现实意义.
CADAS 数据库的统计数据显示,北京首都国际机场、上海浦东国际机场、广州白云国际机场等大型枢纽机场的中转旅客占比仅有4.46%、5.7%与5.87%,目前虽无法构建完善的大规模中转航线网络,但由于我国民航旅客运输量呈现不断增长的趋势,与国外成熟的中转网络相比具有较大的发展潜力,所以在后续研究中将立足于更为成熟的中转网络,考虑在现有模型基础上引入外界气象环境特征,进行更为精准的旅客需求预测研究.
