基于随机森林的城市轨道交通桥梁故障预测模型

2022-02-03郑胜洁徐余明胡祖翰

北京交通大学学报 2022年5期

郑胜洁，徐余明，胡祖翰，刘留

（1.北京交通大学电子信息工程学院，北京 100044；2.中铁第四勘察设计院集团有限公司武汉 430063）

城市轨道交通以其快捷、安全、可靠、环保等特点，逐渐成为人们日常出行首选的交通工具.据统计，截至2021 年12 月31 日，中国共有50 个城市投入城轨交通的建设中，运营线路总计9 192.62 km，其中新增运营线路长度1 222.92 km［1］.在城市轨道交通新增线路的建设过程中，由于建筑物、河流等因素的限制，修建了大量高架桥线路.桥梁在外部环境腐蚀和列车荷载的作用下，其内部结构的耐久性和安全性会受到较大影响，在轨道交通的运营维护过程中需要格外关注［2］.

通过人工现场测试对轨道交通桥梁线路进行维护是目前常用的方式.但是，桥梁人工巡检的方式具有一定的危险性，而且一般是在故障发生之后进行检修，具有滞后性，尤其对于结构位移这种桥梁的关键特征参数，故障滞后产生的影响更大［3-4］.因此，需要建立准确、可靠的城市轨道交通桥梁故障预测系统，对桥梁关键特征参数故障提前预测，以实现早期的故障识别.

城市轨道交通桥梁系统运行数据具有种类多、采样快以及维度高等特点［5］，以轨道交通拱形桥梁为例，桥梁监测数据包括结构位移、结构温度、支座位移、动应变、振动加速度等诸多类型指标，且各类型指标每天采集数以万计的样本数据.因此，如何快速准确找出城市轨道交通桥梁不同监测指标之间的关联性，并对关键参数进行预测，成为国内外学者面临的一个挑战.

机器学习是对桥梁关键参数进行故障预测的一种有效方法，支持向量机、BP 神经网络等算法曾先后用于桥梁故障预测.文献［6］通过支持向量机与粒子群优化相结合的方法，对桥梁震害进行预测.文献［7］采用蚁群算法改进的支持向量机，对桥梁基础群桩轴力进行预测，但在训练大规模样本时要耗费大规模内存和训练时间.文献［8］使用BP 神经网络算法，创建大跨径桥梁结构响应预测模型.文献［9］采用BP 神经网络和GM（1，1）模型组合算法，预测桥梁耐久度.文献［10］使用人工神经网络，对结构位移进行预测.文献［11］采用小波神经网络算法，对桥梁变形进行预测.虽然神经网络在预测时具有较高的精度，但存在网络结构难以确定、易陷入局部最优等问题.

随机森林（Random Forest，RF）是一种分类和回归的集成算法，具有不易陷入过拟合的优点，同时能够降低敏感数据对模型预测结果的影响，在预测应用中可取得不错的效果.文献［12］采用随机森林回归模型，预测了电场的统计特性.文献［13］利用随机森林，预测温室气体替代品的电气强度，并和神经网络做了对比，在相同条件下，随机森林比神经网络的可决系数高了1.5%.文献［14］使用随机森林，预测电力现货市场的出清价格，在相同数据下，随机森林模型比回归树、SVR 和ANN 算法建立的预测模型平均误差分别减少了35.2%、25.3%和26%.此外，在对数据进行回归预测时，应降低无关变量对模型预测的影响［15-16］，因此需要对桥梁的不同监测参数进行特征筛选.特征筛选可以采用相关性系数的方法，而相关性系数可用来判断特征之间是否具有相关性以及相关性的强弱，文献［17］对相关性系数进行了详尽的描述.

综上所述，为了得到一种有效的城市轨道交通桥梁故障预测模型，本文作者以桥梁结构位移参数为例，在原有随机森林回归算法的基础上，与皮尔逊系数特征筛选方法相结合，搭建了基于随机森林算法的结构位移故障预测模型.结合实测数据，分析了随机森林模型的预测性能，并选取了模型性能指标，对比分析了随机森林与其他模型的预测效果.

1 建模关键技术及对象描述

1.1 数据预处理

通过原始数据分析，发现桥梁运行数据中存在一定的异常情况，产生异常的原因主要有3 种：

1）数据缺失.如桥梁监测设备在临时维护时，其所监测的指标将会出现一段时间的零值，若直接对其剔除，则会原始数据序列造成较大损坏.故利用牛顿插值法，对此类异常数据进行修复处理.

2）数据重复.由于数据采样频率过快，在短时间内会出现大量重复数据，如果保留重复数据，后续训练时间会过长，因此需要根据特征之间与特征之内采集数据的相似性，对其进行重复值处理.

3）数据异常.异常数据是离群值，是因为突发的外界环境变化，导致某些监测设备未能及时响应，从而产生异常数据，此类数据对预测的影响最大.

数据预处理就是根据桥梁因以上原因产生的异常数据，进行缺失值、离群值、重复值处理.

1.1.1 缺失值处理

采用牛顿插值法处理缺失数据［18］.以结构位移数据为例，假设结构位移数据f(t)在监测时间节点区间t∈[a，b]内有n+1 个离散点t0，t1，t2，...，tn，其对应的位移数据依次为f(t0)，f(t1)，f(t2)，...，f(tn)，在[a，b]中任给一个t，其对应的因变量为f(t).牛顿插值法第一步要求差商表的值，则n阶差商f(t0，t1，...，tn-1)的计算公式为

式中：f(t0)为自变量t0处函数值；t为任意插值点；t0，t1，t2，...，tn为n+1 个自变量点.

将差商表中所有差商代入式（2），即可求出待插点的位移缺失值.

1.1.2 重复值处理

采用近邻排序算法（Sorted Neighborhood Method，SNM），对数据集重复值筛选处理［19］.先依据不同特征数据，将所采集的数据集分列排列，在桥梁的实测数据中，相似或者相同的监测数据往往相邻排列，因此，可以对所有传感器监测数据设置大小为w的滑动窗口，每次对滑动窗口内各行数据进行相似度筛查，如图1 所示.窗口中的第一行数据和其余w-1 的行数据比较，若符合相似度判断准则，则删除此行数据.采用基于欧式距离的相似度判断，计算窗口内两两特征之间的欧氏距离，若第一行和其余w-1 行数据的欧式距离之差为0，则删除第一行数据.在下次判决中，窗口内最后一行数据的下一行数据可以进入窗口，第一行数据滑出窗口.SNM 处理后，可以消除绝大多数相似或者相同的监测数据.

1.1.3 离群值处理

离群值的处理采用K-means 聚类方法［20］，对于位移数据集f=(f(t1)，f(t2)，...，f(tn))，其包含n个具有T维属性的数据点，聚类算法可以将其划分为K个簇，簇内的点具有高度的相似性，而簇间具有差异性.首先选择K个初始中心点，然后将数据集中的点按平方欧氏距离分配到最近的中心点，从而形成K个簇，并调整各中心点到各簇的平均值.接着重复这一分配调整过程，直至满足收敛判据，或者迭代次数达到上限.迭代结束后，可以实现离群点的识别，接着采用滑动平均［21］的方法替换离群点的值.滑动平均是指沿全长N个数据，不断逐个滑动地取m个相邻数据做直接的算术平均，根据结构位移的实际统计数据特性，对算术平均值设置阈值α，超出阈值的数据即为离群数据，将其用算术平均值替代.

1.2 基于皮尔逊系数的相关性分析

在城市轨道交通桥梁系统中，不同类型的监测数据之间具有一定的联系.例如，当结构温度变化时，结构位移会因为温差对结构的伸缩效应而发生变化.因此，为获得更准确的预测结果，应筛选出与结构位移具有较强相关性的指标.在前期分析数据时，发现数据之间的散点图具有线性关系，并且数据呈正态分布，因此采用皮尔逊系数方法进行相关性分析.皮尔逊系数用于表示特征与其他响应因素之间的关系，取值介于[ -1，1].系数为正值时，表示具有正相关特性；系数为负值时，表示为负相关.皮尔逊系数的绝对值越大，特征之间的相关性程度就越高.假设对于桥梁数据集P={A，B，...，X，Y}，A、B、X、Y分别表示不同类型的监测数据，以A、B两个指标为例，A={α1，α2，...，αm}，B={β1，β2，...，βm}，运用皮尔逊系数（rα，β）进行相关性分析，其计算公式如下

式中：αi、βi为桥梁两类监测指标的数据样本；m为样本数据量.

1.3 基于随机森林的回归预测

随机森林是一种基于回归树模型的集成学习算法，通过对样本数据的随机抽样，组成多个不同的回归树，再把回归树运算结果组合起来，获得随机森林的预测结果.因此，随机森林通常比回归树模型具有更好的拟合效果，在回归预测问题上具有较好的效果.本文建立的桥梁结构位移预测模型，就是运用了随机森林回归的方法.

1.3.1 回归树预测

回归树是决策树的一种，是随机森林的组成单元，其建立过程基于树形结构，主要由根节点、内部节点和叶节点组成.如图2 所示，最上面的是根节点，树的建立过程就是节点不断分化的过程，每一次节点划分都会多一个节点，根节点划分为内部节点，达到划分结束的条件后，最终每个叶节点的输出也就确定.随着模型复杂程度的提高，回归树的规模也随之增大.

图2 随机森林算法结构Fig.2 Random forest algorithm structure

回归树的构建过程如下：首先，选取前文所述的与结构位移具有一定线性相关度的监测特征作为输入变量；其次，将所有训练数据放在根节点，在这些数据中选择最优特征，把根节点二分为两个内部节点，再接着划分特征；最终，将训练集划分为有限个子集.子集的划分过程如下：对于所有输入的特征向量，选择第j个特征向量x(j)作为划分特征，选择s作为划分点，定义两个区域如下

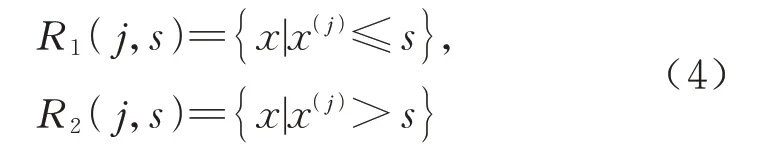
式中：R1(j，s)表示该特征向量划分点的左子树；R2(j，s)表示右子树.

求解下式，可得到最优的划分变量j与划分点s，即

式中：yi表示预测模型的输出值；c1表示左子树的输出变量；c2表示右子树的输出变量.

依次将特征向量集合划分至两个子集.重复上述划分过程.当预测值与真实值的均方误差达到期望值时，或回归树深度达到设定值时，停止划分.

1.3.2 构造随机森林

随机森林是由一系列回归树组成的，它根据Bagging 集成方法来提高算法的准确度（见图2），具体步骤如下：

1）从桥梁监测指标样本集中，有放回地随机抽取n组数据，作为每棵子树的训练集，每组的数据量相同，作为回归树的输入数据.

2）将抽取的n组训练集数据组成n棵回归树，每棵回归树依据1.3.1 节的方法进行分裂，得到对应的回归预测数据，共得到n组结果p1，p2，...，pn.

3）采用平均的方法，将n棵回归树的预测结果综合平均，得到最终的预测结果p，即

1.4 对象描述

本文主要围绕城市轨道交通桥梁监测的历史数据进行模型的构建.城轨桥梁在线监测的数据众多，包括结构位移、支座位移、温度、风向、风速、车速、振动加速度和动应变等参数.为了构建准确的结构位移预测模型，选取某轨道交通拱形桥梁的实测区域，部分监测指标点位的分布如图3 所示.该拱形桥梁监测指标多分布在桥面平面以及桥墩结构连接处，其中共列出6 处结构位移测点，由北至南依次分布在钢桁梁#3、#6、#8、#10 测点以及桥墩#5、#11 测点，有3 处支座位移测点，多分布在墩上下游支座，有6 处温度和动应变测点分布在钢桁梁及拱上弦处.另外，还有横向振动、纵向振动、车速测量、风速风向等多处测点，数据从桥梁监测数据库中采集获得.采样间隔1 s，采样周期14 d，总共304 804 个数据点组成初始数据集.数据集中包含95.3%桥梁正常运作状态数据以及4.7%桥梁故障状态数据，在一定程度上可以覆盖桥梁运行工况的特征.

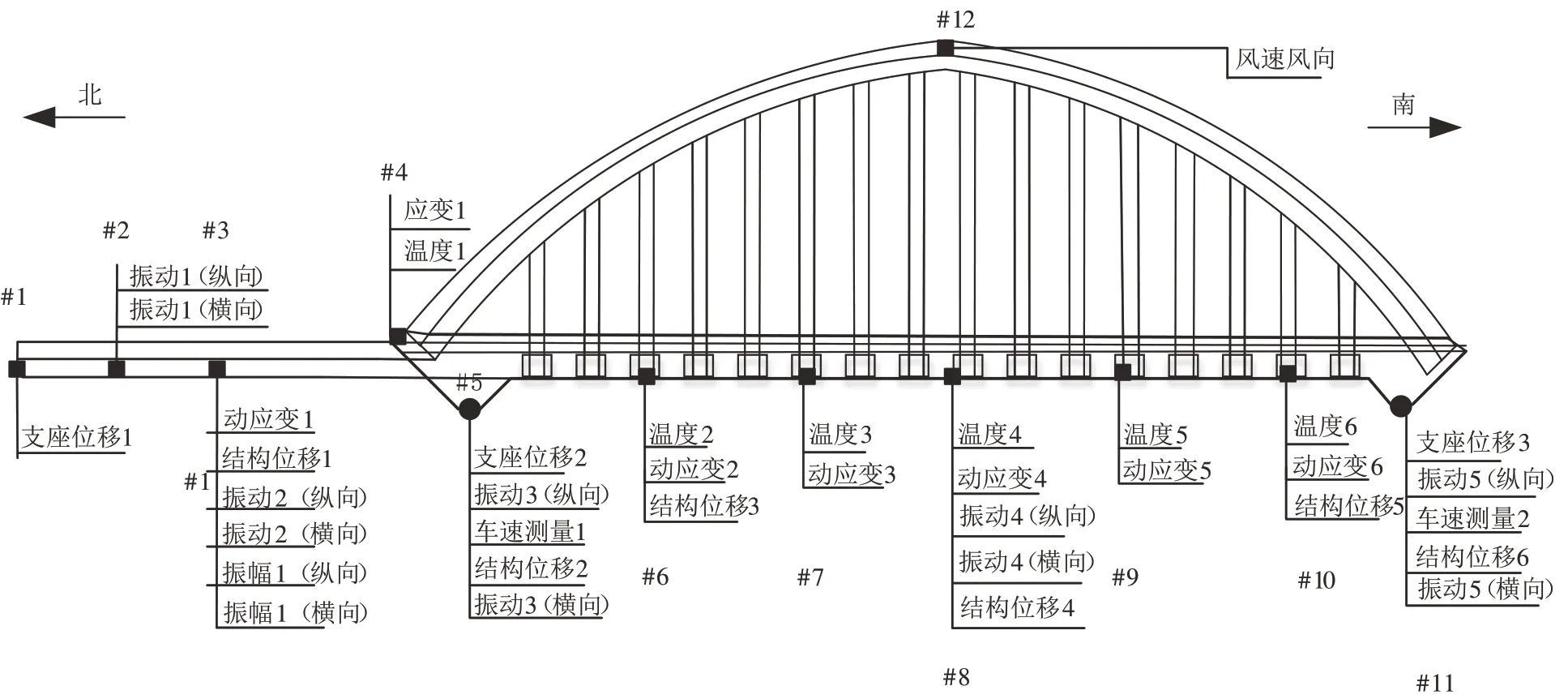
图3 轨道交通拱桥监测指标的点位分布Fig.3 Distribution of monitoring index points on rail transit arch bridges

2 桥梁结构位移建模流程

桥梁结构位移故障预测模型的设计流程为：首先对数据进行预处理与特征筛选，预处理包括对桥梁采集数据缺失值、离群值、重复值的处理，考虑到不同特征因素对桥梁结构位移的影响，特征筛选采用皮尔逊系数分析桥梁所有的传感器测点，接着使用高关联性测点作为模型输入，这样能消除大量低相关性但却导致预测不准测点的影响.将选取的特征输入随机森林回归预测模型，运用正常数据训练出来的预测模型在预测正常桥梁的结构位移时，位移预测值与实际值的残差在一定范围内，而故障状态下其预测值与实际值因残差大于规定阈值而发出预警.整体的预测模型构建流程如图4 所示.

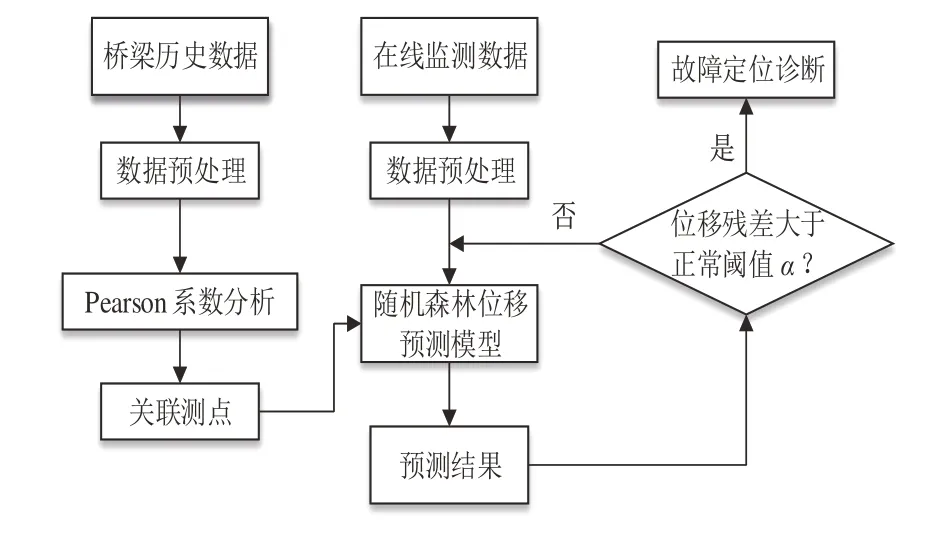
图4 预测模型流程Fig.4 Flowchart of prediction model

2.1 模型数据预处理

数据集中特征包括结构位移、支座位移、温度、风向、风速、车速、振动加速度和动应变等特征，这些参数与桥梁结构位移的相关性不一致，并且呈现高维稀疏特性.比如，桥梁支座会被潮湿的水汽或具有腐蚀性的固体颗粒物腐蚀，造成支座位移数据的异常；在无车经过时，车速和部分加速度传感器没有监测数值.因此，需要将桥梁监测数据中的缺失值、离群值以及重复值处理后再进行分析，图5 为桥梁支座位移经处理后的数据.

图5 桥梁支座位移数据处理Fig.5 Data processing of bridge support displacement

2.2 模型特征选取

在数据处理后，再利用皮尔逊相关系数，对特征之间的相关性进行分析.通过相关性分析，得到桥梁各测点特征的相关性热图，如图6 所示.可以发现，结构位移与动应变、支座位移、结构温度之间的皮尔逊系数均高于0.8，属于显著性相关范围；而其他参数的皮尔逊系数值均小于0.5，属于中等相关以及弱相关范围.考虑到采用较低相关性特征作为输入时会引起位移预测的误差增大，导致无法及时预测故障，因此构建模型时对非显著性相关的监测指标不予考虑.另外，通过对显著性相关监测指标分析，发现它们都分布在桥面平面，并且处于邻近部分的监测区域内，如图7 所示.为此，在对所有监测点位进行相关性分析时，可结合桥梁具体结构优先考虑邻近的监测点位.

图6 桥梁参数相关性热图Fig.6 Correlation heat map of bridge parameters

图7 桥面平面监测点位分布Fig.7 Distribution of monitoring points on bridge deck plane

通过对桥面平面多个测点的分析，得出部分桥面测点数据，如图8 所示.可以发现，结构位移和温度、支座位移具有较高的负相关性，与动应变具有正相关性.因此，可以通过计算特征不同测点的皮尔逊系数，对这些测点进一步分析，作为随机森林预测的输入.

图8 部分桥面平面测点数据Fig.8 Part of the measuring point data on bridge deck plane

将结构位移测点2 作为预测目标，见表1.得出部分相关较强测点与结构位移测点2 的皮尔逊系数.

表1 相关较强测点的皮尔逊系数Tab.1 Pearson coefficients of strongly correlated measuring points

2.3 模型参数设置及评价指标

在经过数据预处理及特征选取后，数据被划分为训练集输入输出特征以及测试集输入输出特征，之后将训练集输入随机森林模型进行训练，并预设参数，表2 为随机森林模型的预设参数.考虑到随机森林子树的数量对预测结果影响较大，因此在实际工程中，通常先将其设置为一个较大数值，以减少误差的影响；同时为了保证训练时间和预测精度，回归树的最大深度设定为一个10～100 之间的随机值；另外，不同特征的输入也会影响训练精度，因此先将全部特征输入，再逐步减少特征数量，分析预测精度最高的特征数量.在实际工程中，叶子节点样本数通常设定为个位数，以保证每个叶子节点区间内的准确性，因此首先将节点最少样本设置为5，再进行交叉验证，以得到最小误差.

表2 随机森林预测模型参数Tab.2 Model parameters of random forest prediction

为准确评判模型的预测性能，选取均方误差（Mean Square Error，MSE）和可决系数R2作为模型性能的评价指标，表达式如下

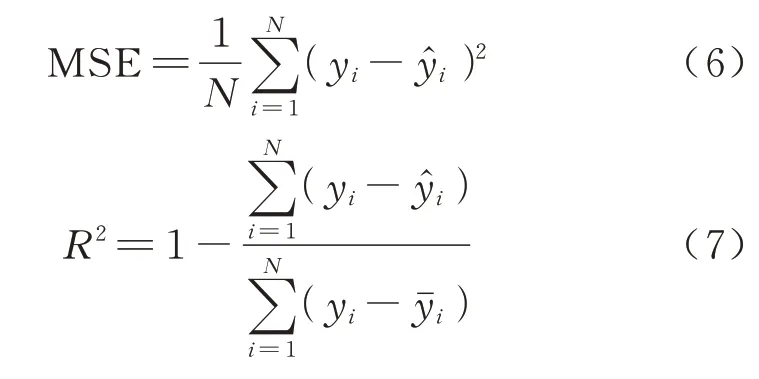
式中：yi为实际结构位移监测值；为位移预测值；为真实值的平均值；N为样本数；MSE 表示预测数据整体的可靠程度，该指标越小表明预测误差越小，即预测结果越可靠；R2表示预测值与实际值之间的拟合程度，在0～1 之间，越接近1 则表示预测效果越好、两者拟合度越好，即预测性能越好.

3 仿真结果验证

为了验证轨道交通桥梁结构位移预测模型的有效性，进行对比实验.选用支座位移、结构温度和动应变监测指标的多个测点数据作为模型训练集输入，结构位移测点2 的数据作为训练集输出，接着在正常数据上训练好模型，然后分别测试模型在设备正常工作时与设备故障时的预测性能.选用某轨道交通拱桥14 d 的正常运行数据作为训练数据集，用来训练桥梁结构位移预测模型，测试集包括一天正常状态和一天故障状态的设备运行数据.考虑到不同类型数据的采样间隔不同，故将采样数据以最小采样间隔进行统一处理，如结构位移采样间隔为1 s，结构温度采样间隔为1 min，则结构温度每秒采样数值与每分钟采样数值统一.经处理后，选取12 982 个数据点，根据模型验证思路，将其中10 982 个数据作为训练集输入模型，剩余数据作为测试集.

3.1 模型预测结果

为验证模型的预测效果，测试集选取一天正常状态数据以及一天故障状态数据.为使预测效果更好，调整了随机森林模型的部分参数，其中对预测效果影响显著的包括随机森林子树棵树以及回归树叶子节点最少样本数，拟合性能由R2和MSE 评估.调整随机森林子树棵树的结果如图9 所示，随着棵树的增加，MSE 和R2逐步收敛，当随机森林子树棵树设置为100 时，MSE 收敛到最小，因此综合考虑训练时间和预测精度，选取100 棵回归树构建故障预测模型，可决系数R2在0.98 左右，均方误差MSE 在0.1 以下.调整回归树叶子节点最少样本数的结果如图10 所示，为保证预测精度，叶子节点样本数一般设置为1～10 之间；由图10 可知，当叶子节点最少样本数为3 时，MSE 最小.

图9 随机森林棵树调整Fig.9 Random forest tree tuning

图10 叶子节点样本数调整Fig.10 Adjustment of leaf node sample number

结构位移测试集在一天内正常状态与故障状态的预测趋势以及预测残差如图11、图12 所示.可见，无论是在正常状态还是在故障状态，随机森林模型都能准确地预测结构位移的变化趋势.其中设定了残差阈值，其设定根据专家主观经验或者数据统计特性决定，一般选取正常状态下残差均方和的2 倍，而为更早地进行故障识别，选取残差均方和作为阈值.在图12 中，数据在第680 个样本点左右处超出残差阈值范围，而越线报警在第850 个样本点左右，因此本方法实现了对故障的早期识别.

图11 正常状态预测Fig.11 Normal state prediction

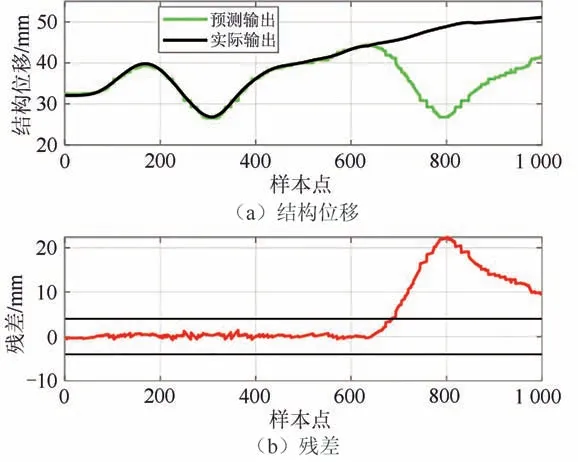
图12 故障状态预测Fig.12 Fault state prediction

3.2 模型对比分析

为了验证随机森林回归算法的预测性能，使用随机森林、SVR、PCR 以及ARMA［22-24］4 种模型，在总计4 000 个数据点的测试集上进行结构位移预测，最后进行效果对比.通过对各类模型调参优化，得到了模型的残差对比，如图13 所示.可以发现，4 种模型的预测残差始终在零点附近波动，上下波动范围基本在-0.5～0.5 之间.

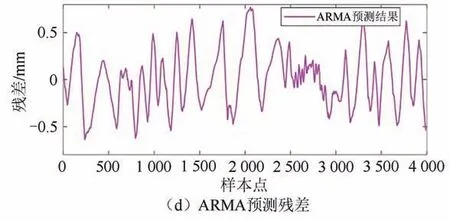
图13 模型对比分析Fig.13 Model comparison analysis

为了更加准确地评价4 种模型的预测性能，用2.3 节中所列的评价指标，对测试集预测结果进行评价分析，根据评价指标的公式，计算出评价结果如表3 所示.

表3 4 种模型性能对比Tab.3 Performance comparison of 4 models

从表3 可以看出，在4 种模型调参后的预测结果中，随机森林预测结果的各项评价指标均优于PCR 和ARMA 的相关指标.其中，随机森林算法的R2达到0.982 1，分别比PCR 和ARMA的指标高1.99%和2.07%，说明随机森林算法的预测值与实际值的拟合程度较好.但是可以看出，SVR 在预测性能上要稍优于随机森林.从训练时间上分析，SVR 的训练时间是随机森林的2 倍以上，而本故障预测对实时性要求较高，因此综合考虑训练时间与预测精度，采用随机森林模型来进行桥梁故障预测效果更好.