三元联系数的一阶全偏联系数中i取值的研究

陆广地，赵克勤

(1.江苏联合职业技术学院 宿迁经贸分院,江苏 沭阳 223600；2.江苏科技大学 计算机信息与技术学院,江苏 镇江 215600;3.诸暨市联系数学研究所,浙江 诸暨 311800)

0 引言

客观事物都以一定的系统形态存在于客观世界,且在不断动态演化.如何用数理方法刻画处于某个瞬时状态的系统在该状态的演化趋势和演化强度,是中外众多数学工作者的任务之一.学者赵克勤先生1989年创立的集对分析原创理论为这方面研究提供了一种新思路：用一个联系数刻画一个系统要素中的部分正常、部分异常、部分反常的状态,简称同异反系统.联系数的偏联系数是刻画这个系统的要素部分正常态、异常态、反常这三部分之间的相互递进和衰减的相互演化的伴随函数[1-3],目前已得到广泛应用,如覃杰、赵克勤(2007)将偏联系数应用于医疗质量发展趋势分析[4]；王传斌、王继顺(2011)将偏联系数应用于对高职教师执行力的潜在分析[5]；马晓燕等人(2012)将偏联系数应用于公众信任度潜在分析[6]；陆广地等(2015)将偏联系数应用于高校评价的排序与聚类分析[7]；门宝辉(2022)将偏联系数应用于地下水开采评估[8]；陈微,赵克勤(2022)将偏联系数应用于学生近视分析[9].但三元联系数的一阶全偏联系数中含有不确定性示性系统i,而如何客观地给出一个i值,会直接影响到一阶全偏联系数的计算.赵克勤(2005)[1]、杨红梅(2019[2]、2021[3])、陆广地(2022[10])分别给出了不同的取值方法.但是最近的研究表明,对于三元联系数的一阶全偏联系数的不确定性系统还存在新的算法,这从一个侧面反映出不确定性系统i取值的复杂性.

1 三元联系数及其一阶全偏联系数

1.1 三元联系数

联系数学是集对的特征函数,其一般形式为

μ=a+bi+cj,其中a、b、c∈[0,1],i∈[-1,1],j=-1,μ∈[-1,1]

(1)

由式(1)知,联系数具有系统性和可计算性等性质，可参考文献[1].

1.2 三元联系数的偏联系数

由文献[1]可知,偏联系数的概念是由赵先生2005年提出,其概念的形成和相应的计算规则主要依据联系数的上述2条性质.具体又分成一阶偏正联系数和一阶偏负联系数,为简明考虑,这些概念可用如下3个定义来体现.

定义1偏正联系数[1]设三元联系数μ=a+bi+cj,假定其中的a原来处于b的层次上,由b正向演化而来.类似地,b是从c层次朝正向演化而来,所以有μ的一阶偏正联系数如下

(2)

定义2偏负联系数[4]设三元联系数μ=a+bi+cj,假定其中的b原来处于a的层次上,由a负向演化而来.类似地,c是从b层次朝负向演化而来,所以有μ的一阶偏负联系数如下

(3)

定义3全偏联系数[5]设三元联系数μ如式(1),其一阶偏正联系数∂+μ和一阶偏负联系数∂-μ的代数和叫做三元联系数的一阶全偏联系数

(4)

式(4)中,j=-1是定义中规定的取值(正负性对立问题),但i+与i-如何在i的定义域[-1,1]中取值,则是一个有待具体分析的复杂问题.

1.3i+与i-取值的一种新思路

在2022年8月6日至10日网络在线举办的全国集对分析第16次学术研讨会上赵先生对i+、i-取值有一个大胆的新算法构想,如下：

(5)

(6)

将式(5)(6)代入式(4)得到一阶偏正联系数的全偏联系数表达式(j=-1)

化简得

(7)

分析如下：

图1 线性系统的两种工作状态(正常与失常)

图2 线性系统S分解成两个子系统S和S图示

把图2①与式(1)进行比较,其演化分量的关系可以用图3①表示.

借用量子纠缠、对立互补思想，系统表面层是正向运动，但其微观层是反向运动.i起调节作用，所以i+在微观上遵从负向运动，按照负向运动的比例原则进行计算，i-也类似如此规律，其差别仅仅在于受到∂b、∂c的影响时，需要添加j这个示性系数作为调节.这也体现了系统的集对思想.

由图3①可知i+应该按照式(5)进行计算.

图3 线性系统S分解成两个子系统S和S的演化分量

同理,再把图2②与式(1)相比较,其演化分量的关系可以用图3②表示.

由图3②类比i+的表达式，可知i-应该按照式(6)进行计算.

需要指出的是，i-给出一个示性系数j(j=-1)体现了其演化方向为负向的符号指示(i+本来是正向，添加j表示方向的指示).

2 算例与应用举例

2.1 算例

例1已知μ=0.2+0.7i+0.1j,求其一阶全偏联系数∂±μ.

解利用三元联系数的一阶全偏联系数的计算公式(4)得

根据前述取值准则,得i+=0.7974,i-=0.8615.代入上式得

2.2 应用

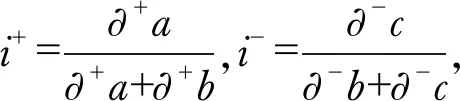
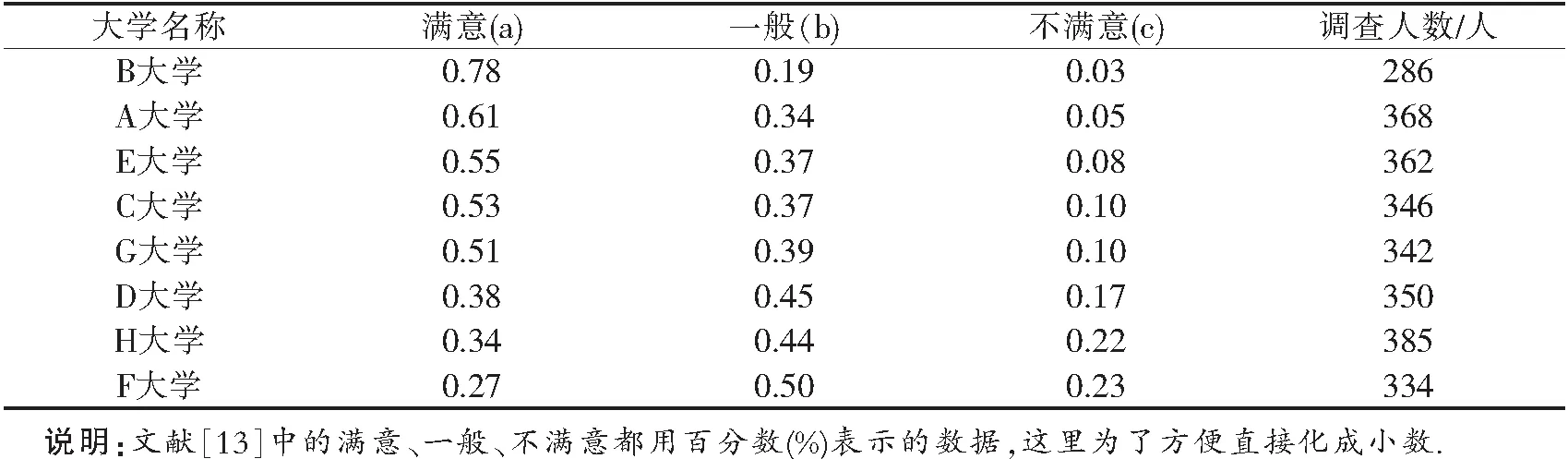
表1 8所著名高校对学生本科教育的满意度评价

数据处理成标准化三元联系数后，再按照本文公式(2)(3)联系数处理，如表2所示.

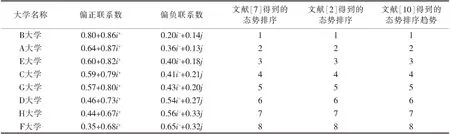
表2 学生对8所著名高校本科教育评价满意度的偏联系数态势排序

将表2联系数中i+与i-使用本文的算法代入算出偏正联系数、偏负联系数,按照公式(4)求出全偏联系数值,再据其值进行态势排序,与文献[7][10]进行比较,如表3所示.

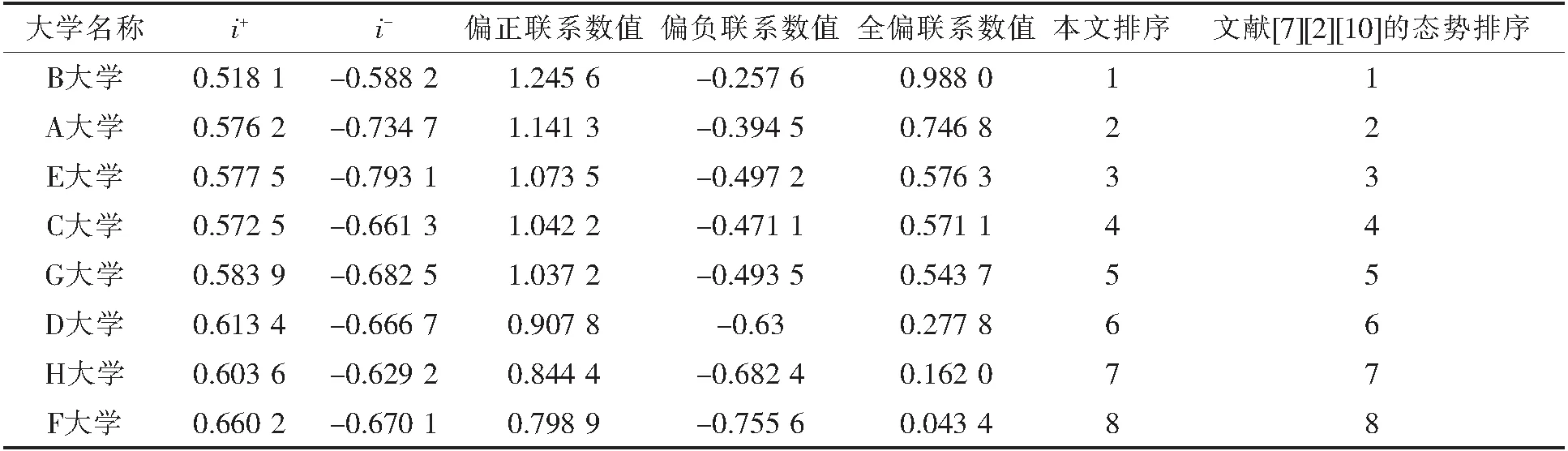
表3 学生对8所著名高校本科教育满意度偏联系数中i+、i-按本文取值的态势排序

从表3可以清楚地看出，本文对i+和i-的新方法与之前文献的态势排序具有内在的自洽性.

3 讨论

3.1 三元联系数一阶偏负联系数的定义演变

文献[4]是2007年文献,其对三元联系数的一阶偏负联系数的定义与2019年的文献[2]中的定义有所不同.文献[4]对三元联系数的一阶偏负联系数的定义是：

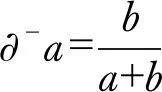
(7)

(8)

(9)

(10)

(11)

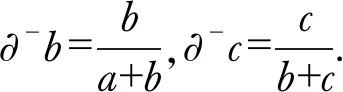
3.2 偏负联系数示性系统取值的不同定义促进辩证思维

1) 事物处在运动和变化之中,客观上存在一定程度的不确定性、不确定性与确定性关系的对立统一性.当用集对分析理论中的三元联系数μ=a+bi+cj描述这类事物时，三元联系数μ=a+bi+cj就成为这类事物的一种数学映射.为此,本文介绍集对分析中的三元联系数μ=a+bi+cj的一阶偏联系数计算原理的历史发展.明确三元联系数的一阶全偏联系数∂±μ=∂+a+∂+bi++∂-bi-+∂-cj是这个三元联系数中相对确定的联系分量a和c与相对不确定的联系分量b之间的相互生成关系和生成过程的数学描述.这也是三元联系数μ=a+bi+cj及其一阶全偏联系数的数学物理意义及其现实意义所在.

2) 集对分析理论的一个巧妙之处在于：为了从数学形式上表明三元联系数的b是不同于a也不同于c的不确定性测度，给b乘上一个能外显其不确定性的示性系数i∈[-1,1],如果需要借助偏联系数客观地阐明当前的三元联系数的客观演化过程时,如何确定i+和i-的值，是一个值得探索的问题.集对分析建立在两个原理之上(成对、系统不确定).成对原理揭示系统演化的两个方向.不确定性原理与量子力学基本思想对于系统功能状态的描述十分相近，特别是量子叠加和量子纠缠.借用量子力学与系统功能状态的内在联系进行研究，用来描述系统故障演化过程的多样性和不确定性.系统功能状态具有如下特点：可靠状态和失效状态组成了功能状态的全域，可靠状态与失效状态没有交集，可靠状态和失效状态是相互动态转化的.系统从表面上看是正向运动，根据量子的互补性与叠加性，其微观层是反向运动，将i+、i-用于调节功能，体现系统微观内部的正反方向的互补性，所以得到本文的取法新思维.

基于以上考虑,本文用2个例子展示了i+、i-的取值准则的应用价值.算例1是一个简单的例子,用来说明取值准则的应用.算例2(实例1)是对笔者以前工作的一个再验证.虽然本文方法与文献[7][2][10]方法所得8个高校学生满意度评价的联系数的数值不同,但其评价数值从小到大的排序完全相同,从而从一个新的视角验证文献[7]的合理性,同时也佐证了本文方法的优越性.

3) 例2揭示提高教育教学质量是高等教育的根本任务.在教育发展的进程中，社会各界包含企业界巨头对目前的教育有许多新看法，比如施一公先生认为研究性大学远远没有发挥潜力，指出我们的人口大国完全应该办出世界一流的高校，培养出世界一流的科学、技术、工程人才，他领衔创办的西湖大学就是一种有效的尝试.华为掌舵人任正非指出中国的教育对学生的创造力培养偏离了方向，他投资创办了附属大学，意为造就适合需要的尖端人才.福耀董事长曹德旺指出教育培养与社会需求脱节，他个人捐献几百亿创办福耀科技大学，坚持建一家不以盈利为目的的高科技大学，根据市场需求来设置专业，使企业招聘与学生就业相匹配，他说不是让中国多一所大学，而是在效仿世界一流高校的做法，希望探索到一条适合并推动中国向前发展的路.这些对我们的教育都有启发意义.从宏观数据中挖掘出有效的信息，分析出潜在的发展趋势，以便在一系列微观细节上强优淘劣，不断改进教育理念、教学方法，整合教育资源，加强教师与教育教学文化，推进符合时代需要的变革，不断提高学生的满意度.本文给出的基于偏联系数的分析方法是一种尝试.对本文的算法与文献[7]进行比较，8个样本的排序完全相同，说明本文的改进算法有自己的价值.

世界是确定性与不确定性的对立统一,对于一阶全偏联系数中的不确定性系数i的取值研究也应遵从这一方针,并结合具体的问题和求解问题的要求作具体分析.从科学与技术的分析情况结合本文的具体算例，表明本文给出的算法有一定的参考意义.