非常规气井产量递减与EUR预测方法评述

2022-02-02崔英敏郭红霞陆建峰张金柏靳广兴赵开良

特种油气藏 2022年6期

崔英敏，郭红霞，陆建峰，杨勇，张金柏，刘伟，靳广兴，赵开良

(1.长庆实业集团有限公司，陕西西安 710018；2.西安锦江能源科技有限公司，陕西西安 710018)

0 引言

不同页岩气田的页岩气产量递减趋势总体一致，均呈初期产量递减幅度大于中后期、递减幅度随生产时间延长逐渐减小的特征。在页岩气井生产后期，页岩气井的产量递减幅度通常很小，主要是由于存在基质补给、吸附气解吸等影响所致[1-3]。不同储层、井型、压力等条件下，页岩气井产量递减特征也略有差异。具体表现为[4-6]：初期产量越大，对应的产量递减率越高；直井、水平井递减指数普遍大于1，说明页岩气井表现为长期非稳态流特征，初期递减率大，一般年递减率为60%～80%；常压与高压页岩气藏生产后期具有相似的递减特征，高压页岩气藏单井初期产量高，但一般初期递减率较常压气藏大。

页岩气井的生产周期较长，产量递减趋势直接影响到页岩气藏的开发投资，因此，研究页岩气产量递减规律极其重要。国内外学者研究了大量的页岩气产量递减分析方法，包括Wattenbarger线性流法、PLE幂指数递减模型法、SEPD扩展指数递减模型法、Duong递减模型法、LGM模型法、连续求解法、拟恒定压力求解法、水平井多级压裂解析模型法等。目前，递减分析方法众多，缺少对各方法适用范围的评价，因此，针对上述方法进行原理、适用性等综合评价，以期在现场实践中能够选择最适用的方法。

1 各类非常规气井产量递减预测方法评价

1.1 Wattenbarger线性流法

页岩的渗透率非常低，流体在页岩气藏中的非稳态线性流动持续时间较长，因此，可以运用解析法估算原始地质储量。Ibrahim、Wattenbarger[7]提出了利用非稳态流动结束时间估算气藏孔隙体积的方程，根据其早期形式得到的原始地质储量计算公式为:

(1)

(2)

fcp=1-0.0852pD-0.0857pD2

(3)

(4)

式中：G为原始地质储量，m3；Ct为储层综合压缩系数，MPa-1；Bgi为原始地层压力下气体体积系数；Sgi为原始含气饱和度；pi为原始地层压力，MPa；pL为Langmuir压力，MPa；VL为Langmuir体积，m3；fcp为受压降影响造成斜率误差的修正因子；pD为无因次压降；ψi和ψwf分别为原始和目前地层拟压力，MPa；mCPL为非稳态流区域直线斜率；T为地层绝对温度，K；h为储层有效厚度，m；xf为裂缝半长,m；K为储层渗透率,mD；ppi为原始地层视压力，MPa；ppwf为目前地层视压力,MPa；telf为线性流持续时间，d；φ为孔隙度，%；μg为天然气黏度，mPa·s；下标i表示气藏初始条件。

式(1)只适用于线性流阶段生产的气井，线性流持续时间的表达式为：

(5)

式中：ye为流动到边界的距离，m。

Wattenbarger线性流法优点为：①考虑页岩气井长期非稳态流特征，可以比较准确地计算页岩气井可采储量；②可对页岩气井地层流动状态进行有效判别；③引入页岩气吸附特征参数Langmuir压力pL和Langmuir体积VL，能够对页岩气直井、多级压裂水平井进行可采储量计算，包括吸附气储量和游离气储量。其局限性为：在计算之前，需要准确确定页岩渗透率参数，但由于页岩超低渗透率的特征，其不确定性较大，不同的渗透率取值将直接影响拟线性流结束时间，对最终页岩气井可采储量预测具有较大影响。

1.2 PLE幂指数递减模型法

该方法由ILK教授最先提出，故又称ILK递减模型法[8-9]。该方法根据Arps递减理论提出了幂指数递减形式，从而代替传统的双曲递减，能较好地分析致密气藏和页岩气藏递减规律，并进行单井可采储量的预测。

PLE幂指数递减模型与常规Arps方法类似，同样需要定义递减率和递减率指数。ILK通过大量实际数据分析，得出了连续性递减率，其表现出一种幂指数变化规律，因此，根据PLE幂指数递减率的变化趋势可以将产量描述为：

(6)

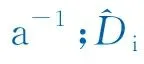
PLE方程是扩展指数方程的原型，当D∞=0时，式(6)为扩展指数方程。PLE幂指数递减模型的优点为：①该模型为非常规气藏预测可采储量(EUR)的计算模型，计算结果优于常规Arps递减模型；②对非稳态流及拟稳态流数据均能很好地拟合；③可分析致密页岩气藏递减规律及多层合采气藏的递减规律；④更容易辨别不同的流态，有效区分瞬态流和边界控制流；⑤能够在早期准确地预测页岩气井单井可采储量。其局限性为：①井间干扰对预测结果的影响较大，对数据点的敏感性较大，分析前需对实际数据进行微分平滑处理或平均化处理；②频繁开关井对预测结果的影响较大；③拟合参数时需要不断重复调整，耗时长，且需要编制软件。

1.3 SEPD扩展指数递减模型法

Valkó和Lee提出了类似PLE模型的递减分析新方法，称为SEPD扩展指数递减模型法[10]，该方法是通过对Barnett页岩气藏7 000多口井的生产数据进行统计研究而得出的。

SEPD模型中产量随时间的变化关系为：

(7)

式中：τ为由历史产量数据拟合而得的待定系数。

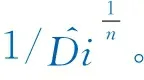
SEPD扩展指数递减模型优点为：①该模型为非常规气藏EUR计算模型，计算结果优于常规Arps递减模型；②能够比较准确地分析致密页岩气井递减规律；③能够更容易辨别不同的流态，有效区分瞬态流和边界控制流；④提供了累计产气量随时间变化的计算公式，可以更容易、平滑地对离散趋势的生产数据进行拟合。其局限性为：①对数据点的敏感性较强；②不能够对页岩气井最大可采储量进行早期预测，当页岩气井达到拟稳定流后，预测结果才比较可靠，EUR结果整体表现比较保守；③拟合参数时需要不断重复调整，耗时长，且需要编制软件。

1.4 DUONG递减模型法

qg(t)=qit-n

(8)

式(8)中，n的取值为0.50(线型流)或0.25(双线型流)。为了使该公式能够更灵活地对生产数据进行拟合，Duong引入了参数m作为t的指数形式：

(9)

式中：a、m均为模型中的待定系数。

Duong递减模型优点为：①该模型为非常规气藏预测产量和可采储量的计算模型，计算结果优于常规Arps递减模型；②该模型能够较好地对页岩气井非稳定流阶段数据进行拟合；③能够在早期对页岩气产量和可采储量进行预测。其局限性为：①该模型对数据点的敏感性较强，分析前需对实际数据进行微分平滑或平均化处理；②模型曲线中不能直接观察到后期拟稳定流阶段的特征；③Duong模型须进行修正后才能对后期拟稳定流数据进行拟合；④拟合参数时需要不断重复调整，耗时长，且需要编制软件。

1.5 LGM模型法

Clark等提出了可用于单井预测的罗杰斯特模型(LGM)[12]：

(10)

式中：Qf为不考虑经济条件的单井极限预测最终可采储量，108m3；α为采出50%极限可采储量所需的时间，月。

LGM模型优点为：①该模型为非常规气藏(井)预测产量和可采储量计算模型，计算结果优于常规Arps递减模型；②该模型能够较好地对页岩气井非稳定流阶段及拟稳定流阶段数据进行拟合；③能够较好地对页岩气井流动状态进行划分。LGM模型局限性为：①对数据点的敏感性较强，分析前需对实际数据进行微分平滑或平均化处理；②模型受极限预测最终可采储量控制，当极限预测最终可采储量未知时，该模型预测结果可能存在多解性；③拟合参数时需要不断重复调整，耗时长，且需要编制软件。

1.6 可采储量连续求解法

Currie 等创建了一种连续求解预测技术[13]，并用于致密气井和页岩气井的产量和可采储量预测。该连续预测技术是一种使用多组时间间隔的生产数据分别预测产量和可采储量的过程。在气井达到边界控制流之前为气井提供预测的上、下限值，有利于降低预测的不确定性。实际上该方法整合了常规Arps递减方法和现代递减模型法(PLE、Duong等)，为非常规气井提供可采储量的上限值，并使用线性外推技术来求取页岩气单井可采储量的下限值。可采储量的上限值与时间为递减关系，下限值与时间为递增关系，上、下限值最终均收敛于一个准确的气井可采储量值。可采储量连续求解法的优点为：①该模型更加系统地整合了常规Arps模型以及现代递减模型(PLE、Doung等)；②考虑了可采储量与时间的变化关系，能够对可采储量进行动态预测；③能够得到页岩气井可采储量预测上限及下限值，有效降低可采储量预测的不确定性。其局限性为：①该方法对数据点的敏感性较强，分析前需要对实际数据进行微分平滑处理或平均化处理；②该方法只适用于连续生产的页岩气井；③模型求解时间耗费长，需要编制软件。

1.7 拟恒定流动压力求解法

常规Arps递减模型以及现代递减模型(PLE、SEPD、Duong、LGM等)常用来预测页岩气单井可采储量，然而，只有气井具有恒定的井底流压或具有恒定的压降条件才能降低页岩气井可采储量预测的不确定性。当页岩气井油嘴大小调整或频繁开关时，产气量、压力波动频繁，而当页岩气井进行了限产生产后，其产量会在较长时间内保持恒定，此时，以上方法在预测产量和可采储量时，将会增加预测的不确定性。

支撑组件实际提供的稳定支撑力大约为M0=2.8N，代入式(6)计算可得传感器自身的系统测量误差δ=0.45%。伸杆组件的支撑力精度主要包括压力传感器测量误差和支撑组件因转动而引入的支撑力误差两项，故系统误差总和为0.45%+0.7%=1.15%，该值在合理范围之内。因此综上所述，伸杆支撑组件在上述展开方法中的卸载效率均满足设计要求。

Xie等[14]通过对Haynesville页岩气藏限产页岩气井产量和可采储量进行研究，提出了拟恒定井底流动压力法，对限产井或压力、产量波动的页岩气井进行单井产量和可采储量进行预测。该方法源于气体产能指数的压力特征化处理：

(11)

式中：q为日产气量，104m3/d；qN为压力特征化日产气量，104m3/d；pwf为井底流动压力，MPa；pwfa为废弃井底流动压力，MPa；F为拟压力函数，MPa2/(mPa·s)。

将计算出的压力特征化日产气量数据与累计产气量绘制于半对数坐标图版中，用于求取页岩气井单井可采储量。拟恒定流动压力求解法的优点为：①引入压力与产量2种因素，对日产气量进行压力特征化处理，考虑的因素更全面；②能够对限产井、变井底流动压力井进行单井预测。其局限性为：①对井底流动压力数据具有较高的要求，在进行预测前，需要对页岩气井的井底流动压力进行折算，折算结果存在一定的不确定性；②该方法仍具有产量递减分析技术预测页岩气井长期递减中所固有的不确定性；③该方法目前只在少数页岩气田内进行测试，对于不同页岩气田的适用性还有待于进一步研究。

1.8 水平井多级压裂模型解析法

水平井多级压裂模型解析法优点为：①考虑了井型、储层内外边界对页岩气井生产的影响；②考虑了气体PVT性质随压力的变化情况；③能够对限产井、变井底流动压力井进行历史拟合并预测单井可采储量；④考虑了不同流动状态对页岩气井生产的影响。其局限性为：①对井底流动压力数据具有较高要求，在进行预测前，须对页岩气井的井底流动压力进行折算，折算结果存在一定的不确定性；②储层物性参数如基质渗透率、裂缝半长、裂缝传导率等参数的确定存在较大不确定性因素；③计算复杂，耗时长，需要专门软件进行模拟计算。

2 非常规气井产量递减分析与可采储量计算方法评价

2.1 页岩气可采储量计算方法对比

表1为国内外主要使用的各种产量递减和EUR预测方法适用条件，表2为Lee对目前北美流行的各种产量递减预测方法的适应性评价[19]。

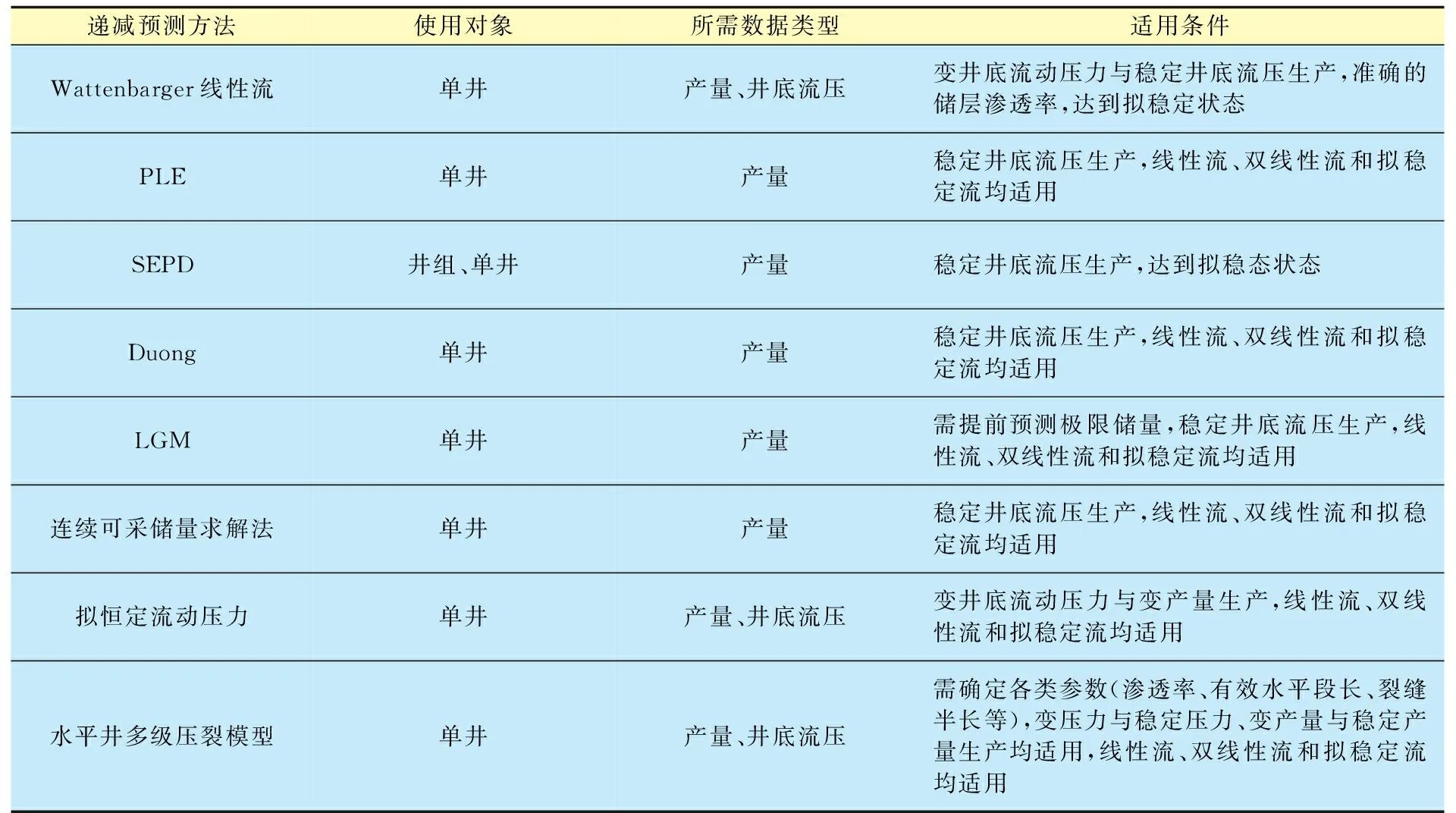
表1 不同非常规气井产量递减预测方法适用条件对比Table 1 The comparison of applicable conditions for different production decline prediction methods for unconventional gas wells

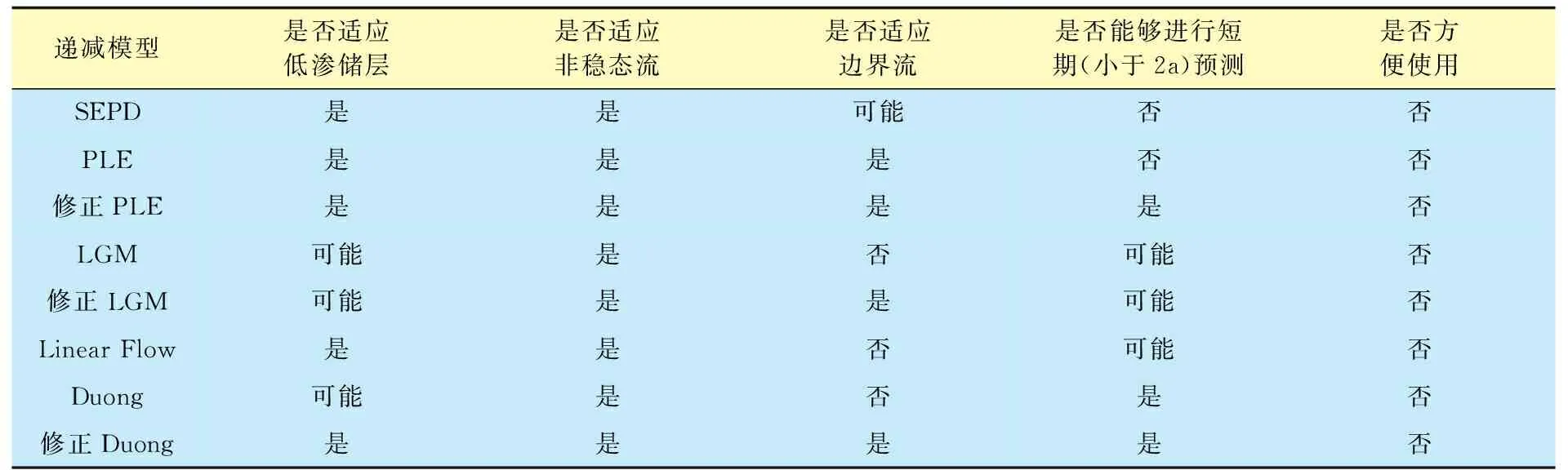
表2 北美常用非常规递减模型适应性评价Table 2 The adaptability evaluation of unconventional decline models commonly used in North America

由表1、2可知：各种方法均适用于线性流、双线性流和拟稳定流等地层流态；Wattenbarger线性流、拟恒定流动压力、水平井多级压裂模型3种方法更适用于变产量、变井底流压的流动状况，其他几种方法则需要在预测区间内具有相对稳定的井底流压；各种方法进行短期预测(小于2 a)时的可靠性也不尽相同。

2.2 模拟井验证分析对比

由前文分析可知，不同的流动状态下，页岩气井的递减特征和可采储量预测也会存在不同的结果，页岩气井在实际生产过程中，主要的流动状态为线性流、线性流+边界控制流2个流动阶段。为研究不同流动阶段下各种递减模型的适应性，开展PLE、SEPD、Duong、LGM 4种递减模型的适应性研究。将4种递减模型预测的结果与页岩气模拟井数值模拟研究预测的结果进行比较，数值模拟模型中考虑了页岩气的解吸、扩散、渗流等过程，更符合页岩气地层实际流动规律，其预测结果相对可靠。页岩气模拟井参数见表3。假设不同流动状态下，模拟井SRV体积不变，且连续生产。流体先由基质向人工缝流动再向井筒流动。

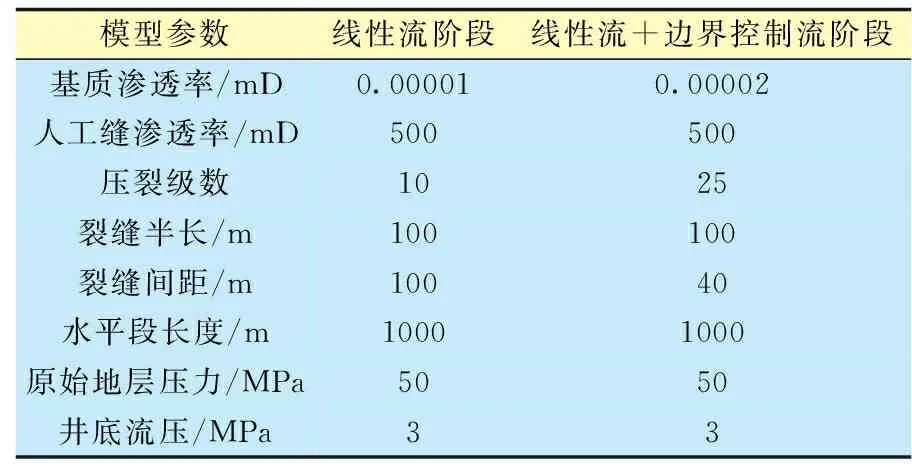
表3 模拟井不同流态下的参数Table 3 The parameters of simulated wells under different flow regimes

2.2.1 线性流模拟预测

对于页岩气井，若基质渗透率过低，则气井经济开采时间内不会发生边界控制流动，线性流结束时间将大幅度延后。当生产时间足够长，页岩气井仍能够达到拟稳态流动阶段。因此，设定生产时间为30 a，当30 a内页岩气井仍未出现拟稳态流，则仅计算30 a的累计产气量。

不同时间段不同预测方法的预测结果见图1、表4。由图1可知：生产30 a时，日产气量与生产时间的双对数表现为斜率为0.5的线性特征；SEPD、LGM模型在后期出现偏离线性的趋势，PLE、Duong模型在后期依然表现为直线特征。

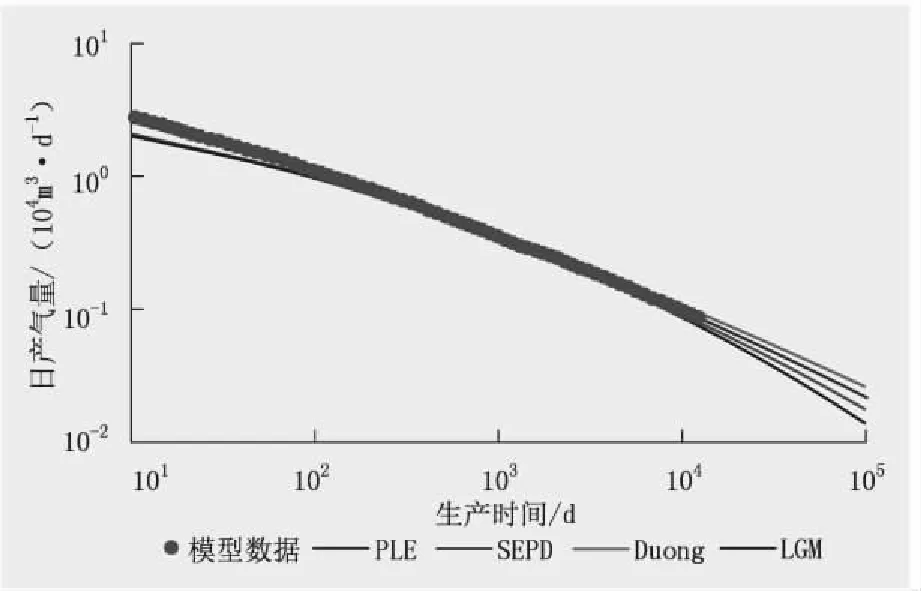
图1 线性流阶段各模型预测日产气量Fig.1 The daily gas production predicted by each model in the linear flow stage

由表4可知： SEPD模型早期(100 d)预测结果偏低，预测结果比较悲观；PLE、Duong、LGM模型早期(100 d)预测结果与模拟模型预测的累计产气量0.107 6×108m3相比偏低，但误差在可接受范围之内，随着时间的增加，模型预测精度逐渐增加；由于模型在模拟时间结束时(30 a)，仍然处于线性流阶段，故所有模型预测结果均为30 a的最大累计产气量，并非真实气井可采储量。

表4 线性流阶段各模型预测累计产气量Table 4 The cumulative gas production predicted by each model in the linear flow stage

2.2.2 线性流复合拟边界控制流模拟预测

线性流复合拟边界控制流(线性流和边界控制流)与线性流特征类似，只是在模拟结束后的时间(30 a)内表现出了拟边界控制流特征，即日产气量与生产时间的双对数表现出斜率为-1.0的特征(图2)。4种模型预测累计产气量结果见表5。

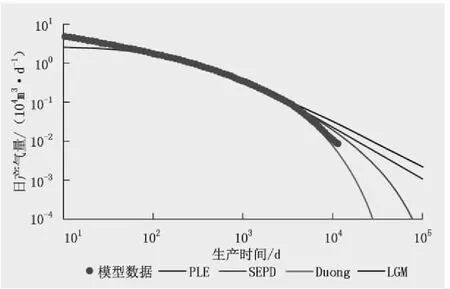
图2 线性复合拟边界流阶段模型拟合Fig.2 The model fitting in the linear composite quasi-boundary flow stage

由表5可知：在线性流复合拟边界控制流阶段，随着拟边界控制流的出现，4种递减模型预测可采储量的精度逐渐提高；此外，多数递减模型在早期(小于1 a)均不能有效预测单井最终可采储量，但LGM模型则能够在2 a内对单井可采储量的预测精度较高，其他模型预测的结果相对偏高。

表5 线性复合拟边界流阶段各模型预测对比Table 5 The comparison of predictions of various models in the linear composite quasi-boundary flow stage

以数值模拟预测的页岩气井可采储量作为对比参照值存在一定缺陷：目前数值模拟模型并不能将页岩气的流动机理完全反应出来，预测结果可能与实际井的生产结果出现较大偏差，该文仅作为一种参考，还需要实际生产井的对比评价和验证。

2.3 实例验证

以墨西哥Arcabuz-Culebra致密气藏Coapa PEMEX气井为例。该井已生产44 a，周围无其他井干扰，储层渗透率小于0.001 mD，储层厚度为105 m，为连续性较好、厚度较大的致密砂岩储层。由于该井具有较长生产历史，可以有效对各种递减模型进行拟合检验。

4种递减模型在早期(生产1～3 a)对该井的预测结果见图3。由图3可知：各模型随生产时间的增长，预测结果与实际数据的误差逐渐减小；LGM和SEPD模型预测结果误差较大，预测结果较为保守；PLE和Duong模型拟合误差较小，预测结果相对准确。

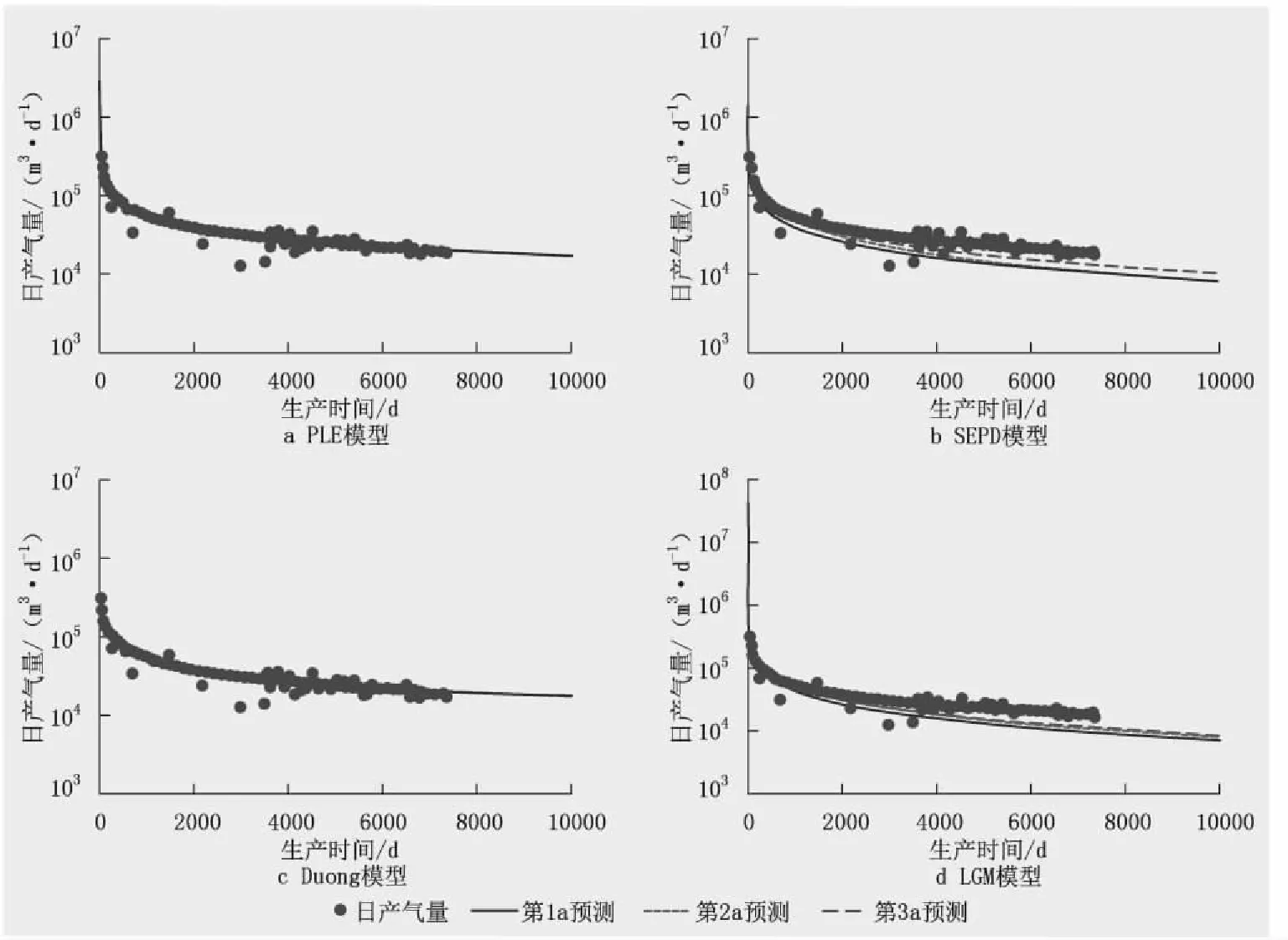
图3 Coapa PEMEX气井不同递减模型拟合结果Fig.3 The fitting results of different decline models for Coapa PEMEX gas wells

综上所述，同一模型不同页岩气井流动阶段和不同模型同一流动阶段的预测结果相差较大。目前非常规气井产量递减与EUR预测方法较多，在线性流阶段或生产时间小于1 a，无论哪种模型的预测准确性均较差；在线性流复合拟边界控制流或生产时间超过1 a时，各种模型预测的准确性明显提高，其中，PLE和Duong模型短期2 a内预测更为准确。此结果对于在不同流动阶段选择合理的模型以及在合适的生产阶段进行产量递减与EUR预测均具有重要的指导意义。