有限群广义表示的进一步研究
2022-02-02刘秀
刘 秀
(昭通学院数学与统计学院,云南 昭通 657000)
群论中的一种重要的研究方法是研究给定的群G到另一个群W的同态,通过了解群W的结构来认识群G的结构,这是现代数学的一个鲜明的特征.如群论学者通过研究群G到集合Ω 上的对称群SΩ的同态映射,即研究群G在集合Ω 上的作用,得到著名的轨道-稳定子定理,Sylow 第一、第二、第三定理[1-2].群表示论是群论的一个重要分支,经典群表示是研究群G在向量空间V上的作用,即研究群G到GL(V)的同态映射,这种群表示叫线上表示.当选定V的一个基后,GL(V)与GL(n,F)是同构的,群表示也可看成是G到GL(n,F)的同态映射,这种群表示叫矩阵表示[1,3-4].当然,群的线性表示和矩阵表示本质上是相同的,只有形式上的不同.群表示论由G.Frobenius 所创立,对群论本身及对结晶学、物理、化学等其他学科有着广泛的应用.
广义同态也是一种保持运算的映射[5],通过研究群的广义作用[6-11],我们已得到了许多与后续研究相关的重要结果.在文献[12],我们引入了广义线性表示这一概念,通过研究群G在向量空间V上的广义作用,我们得到了与群G结构相关的几个重要结果.本文在文献[12]的基础上,通过研究群的广义线性表示和广义矩阵表示,获得若干有用的群结构信息,推广了一些熟知的结果.当然,我们在谈群的广义表示时不再区分是线性表示还是矩阵表示,而是视讨论问题的需要选择所采用的形式.
本文中,F 是一个域,GL(V)表示V的全体可逆线性变换组成的乘法群,GL(n,F)表示F 上全体n×n可逆矩阵组成的乘法群.
1 预备知识
定义1[12]设G是一个群,是域F 上的一个向量空间.G到GL(V)的一个广义同态φ称为G的一个广义线性表示(简称广义表示).V称为表示空间.若V是有限维的,则V的维数dimFV称为广义表示的级(或次数).
定义2[12]设φ:G→GL(V)是一个广义表示.称广义同态核Ker为表示φ的核.如果Kerφ=G,则称φ称为G的平凡广义表示.如果Kerφ=1,则称φ称为G的忠实广义表示.
定义3群G到GL(n,F)的一个广义同态φ称为G的一个广义矩阵表示.F 叫广义表示的基域.矩阵的阶n叫广义表示的级(或次数).

2 主要结果
引理1设群G在集合上有一个广义作用,可按下述步骤构造G的一个域F 上的n次广义表示.
步骤1:构造F 上n维线性空间V.
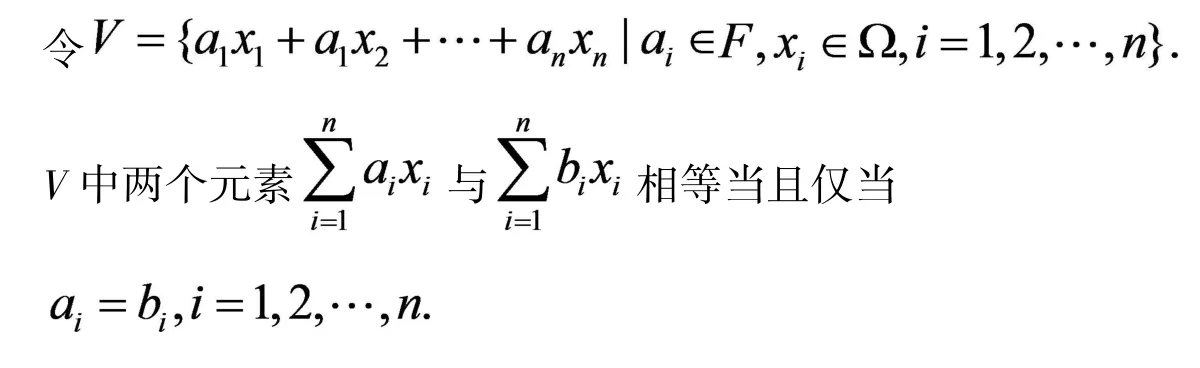
在V中规定加法运算和数乘运算分别为:
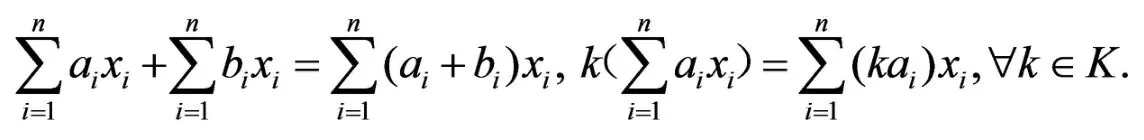
易证V成为域F 上的线性空间.

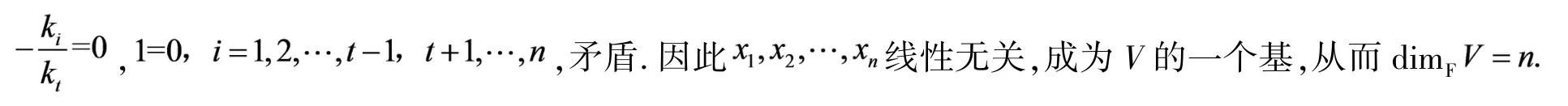
步骤2:构造群G到GL(V)的广义同态映射φ.

引理1 详细给出了构造群的n次广义线性表示的操作方法.

定理1 的意义在于通过研究较具体的一般线性群或矩阵群去获知抽象群的结构,这是研究群的最有力的方法之一.
例1求n元对称群Sn在域F上的n次置换广义表示.

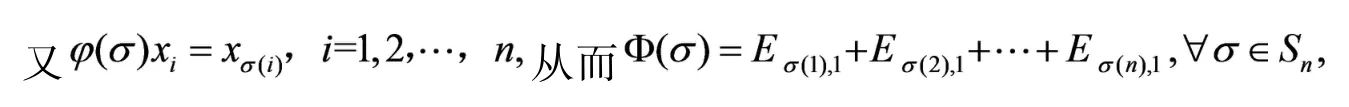
其中Ei,j是第i行,第j列元素为1,其余元素全为0 的矩阵.
例1 通过研究n元对称群Sn到GL(V)的广义同态,实现通过了解熟悉的群GL(V)的性质来认识Sn的结构.
例2求3 元对称群S3在域F上的3 次置换广义矩阵表示.

因此φ对应的矩阵表示为:

例2 把S3的元素映射为3 阶矩阵,使得对S3的研究更具体、更直观.


例3 把n阶循环群G等同于Φ(g),Φ(g2),…,Φ(e)构成的乘法群,结果体现矩阵的对称美.



例5 的技巧在于选取表示空间V的基为S3的元素,在同构的意义下,我们可把对S3的研究转化为对6 阶矩阵群的研究,这是有效的方法之一.
