层状graphene/WSSe范德瓦耳斯异质结电子特性和界面接触的理论研究

赵婷婷

(1.大连理工大学材料科学与工程学院，大连 116024；2.大连理工大学，凝固控制与数字化制备技术重点实验室，大连 116024)

0 引 言

自2004年首次发现石墨烯(graphene)以来，其独特的物理和化学性质[1-2]，如狄拉克锥[3]、高电导率和载流子迁移率[4]以及霍尔电导率的半整数量子化[5]，引起了科学工作者的极大兴趣和关注。然而，由于石墨烯带隙宽度为零，其在场效应晶体管中的应用受到限制。因此，迫切需要找到有效的方法来改善graphene 的电子特性以拓宽其在纳米电子和光电子器件中的应用范围。科研工作者已经尝试诸多方法来调节graphene的电子特性，例如掺杂[6]、氢化[7]和尺寸效应[8]。此外，通过不同层状材料堆叠构建范德瓦耳斯异质结不仅能够继承母材的电子特性[9]，还能产生一些新的性质，打破单层材料应用的限制。

过渡金属硫化物具有类似石墨烯结构，其单层是上下两层硫族元素中间包夹一层过渡金属元素，由于其半导体特性及超导电性受到研究人员的广泛关注。自从通过化学气相沉积法合成Janus MoSSe以来，新型过渡金属硫化物Janus MXY (M=Mo, W; X/Y=S, Se, Te, X≠Y)进入人们视野[19]。其中，Janus WSSe单层W原子通过共价键与两侧的S和Se原子连接，由于结构的不对称性会在该材料上形成固有的平面外电场，这种独特的结构使其在纳米电子器件中表现出巨大的应用潜力，并且已有文献报道借助化学气相沉积法制备了WSSe单层结构[20]。Dong等[21]揭示了在器件应用中采用压电MXY (M=Mo, W; X/Y=S, Se, Te, X≠Y)及其范德瓦耳斯异质结的可能性。双层或者多层WSSe的电子特性可以通过控制硫族元素原子层顺序来调节[22]。最近，研究人员对Janus MXY和graphene单层构建的范德瓦耳斯异质结已经展开了一些探索，如graphene/MoSeS/graphene[23]、graphene/MoXY[24]、graphene/MoSeS[25]。理论计算表明改变本征偶极矩的方向会影响肖特基势垒高度，导致p型和n型肖特基接触之间的转变[26]。受这些graphene基范德瓦耳斯异质结的启发，本文借助第一性原理计算方法对graphene/WSSe的电子特性和界面性能进行了探究，结果表明graphene/WSSe的能带结构可以被视为两个单层材料能带结构的叠加。在层间距为0.341 nm的情况下，graphene与WSSe 形成n型肖特基接触。通过调整层间距和外部电场，可以有效调节graphene/WSSe的接触类型和SBH。这些结果为新型graphene基异质结光电子和纳米电子器件的设计和制造提供了理论依据。

1 计算方法

本文中的所有计算均是基于密度泛函理论(density functional theory, DFT)在CASTEP模块进行。选择广义梯度近似(generalized gradient approximation, GGA)的Perdew-Burke-Ernzerhof (PBE)[27]来描述交换相关泛函。借助超软赝势(USP)方法处理电子-离子相互作用。由于密度泛函理论方法无法准确描述以范德瓦耳斯力为主的弱相互作用异质结，借助Tkatchenko-Scheffler (TS)对其进行了色散修正，DFT-TS方法合理地描述了层间的长程范德瓦耳斯相互作用。在垂直异质结方向施加了2 nm真空防止两个周期材料之间的相互作用。截断能的取值大小为500 eV，自洽场收敛标准为5×10-6eV/atom，原子间相互作用力的收敛阈值设置为0.01 eV/Å(1 Å=0.1 nm)。最大应力和最大位移分别为0.05 GPa和1×10-4nm。分别选取4×4×1和6×6×1 的k点网格用于几何优化和能量计算。相应原子的价电子分别为：C-2s22p2，S-3s23p4，Se-4s24p4和W-5d46s2。

2 结果与讨论

2.1 结构稳定性

在对graphene/WSSe性能计算之前，本文先对graphene和Janus WSSe单层的结构进行了优化，两者的晶格常数分别为0.246 nm和0.324 nm，接近文献报道数值[28-29]。为了获得低晶格失配率的计算模型，分别构建4×4×1的graphene单层和3×3×1 的Janus WSSe单层，这两种单层的晶胞尺寸分别为0.984 nm和0.972 nm。此时，搭建的graphene/WSSe异质结的晶格失配率为 0.7%, 满足完全共格要求，即晶格失配率小于5%。

在构建graphene基范德瓦耳斯异质结时，二维单层的取向不容易控制。考虑到垂直方向graphene和Janus WSSe取向差异，本文构建了两种堆叠模型，如图1(a)和(b)所示。又由于与graphene单层邻近的硫族原子层可以是S或Se原子层，如图1(c)和(d)所示，因此，本文共搭建了四种graphene/WSSe异质结模型，分别称为Ⅰ型、Ⅱ型、Ⅲ型和Ⅳ型。

图1 四种构型graphene/WSSe的顶视图和侧视图Fig.1 Top and side views of four configurations of graphene/WSSe

为了考察graphene/WSSe异质结的结构稳定性，根据公式(1)对结合能(Eb)进行计算:

Eb=(EH-EG-EWSSe)/NC

(1)

式中：EH、EG和EWSSe分别表示异质结、孤立graphene和Janus WSSe单层的总能量。NC表示graphene/WSSe异质结中总的碳原子数。由表1可知，四种graphene/WSSe异质结(Ⅰ型、Ⅱ型、Ⅲ型和Ⅳ型)对应的每个C原子的结合能分别为-61.39 meV、-61.43 meV、-63.60 meV和-63.66 meV，这与文献报道graphene基异质结的值相当[7]，反映了graphene/WSSe异质结层间相互作用为范德瓦耳斯力。此外，四种异质结的平衡层间距离分别为0.346 nm、0.347 nm、0.340 nm和0.341 nm，这与其他异质结报道值相近，如MoS2/ZnO[30]，进一步验证了graphene和WSSe单层相互作用为范德瓦耳斯力。另一方面，计算了电子局域函数，深入探索Ⅰ型、Ⅱ型、Ⅲ型和Ⅳ型graphene/WSSe异质结中两个单层之间的成键情况，如图2(a)～(d)所示。从图2能够看出四种异质结中graphene和WSSe层间没有明显的电子累积，同样验证了两个单层材料是通过范德瓦耳斯力相互作用的结论。此外，根据前面的计算结果不难发现堆叠方式对graphene/WSSe异质结的电子和结构性质影响很微弱，本文选择相对更为稳定的Ⅳ型异质结作为进一步计算的对象。

表1 四种构型graphene/WSSe的结合能(Eb)和平衡层间距(DE)Table 1 Binding energy (Eb) and equilibrium interlayer distances (DE) of four configurations of graphene/WSSe

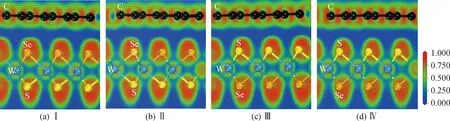
图2 Ⅰ型、Ⅱ型、Ⅲ型和Ⅳ型graphene/WSSe的电子局域函数Fig.2 Electron localization functions of graphene/WSSe for Ⅰ, Ⅱ, Ⅲ and Ⅳ pattern

2.2 电子特性

为了了解graphene/WSSe异质结的电学性质，计算graphene、WSSe单层和graphene/WSSe异质结的能带结构，如图3(a)～(c)所示。由图可知，graphene具有线性色散关系，于倒易空间K点形成狄拉克锥，表现出零带隙能带结构，这说明了graphene的金属特性。Janus WSSe表现出直接带隙，GGA-PBE泛函计算得到带隙宽度为1.727 eV，HSE06泛函得到带隙宽度为2.176 eV，与文献结果一致[31-32]。从图3(c)中可以看出，graphene/WSSe异质结中graphene的带隙打开了7 meV，这与graphene/SnO中的报道值相当[33]。因此，通过与WSSe结合可以有效地提高graphene的光电性能，有利于其在电子器件中的应用[34]。另外，graphene/WSSe异质结的能带结构是单层graphene和Janus WSSe能带结构的简单加和，主要是由于异质结的两个单层之间通过范德瓦耳斯力结合。图3(d)显示了graphene/WSSe异质结的总态密度(total density of states, TDOS)和分态密度(partial density of states, PDOS)。显然，graphene/WSSe异质结在费米能级(EF)附近主要由graphene贡献，且很好地保持graphene狄拉克点附近的线性色散关系。

依据金属/半导体界面的肖特基-模特模型[15]可以获得：n型肖特基势垒高度(n-type SBH,ΦBn)为导带底与费米能级的能量差，p型肖特基势垒高度(p-type SBH,ΦBp)代表价带顶和费米能级的能量差值。图3(h)显示了graphene/WSSe异质结界面接触类型的示意图。从图3(c)可知，graphene/WSSe异质结的导带底相比于价带顶更接近费米能级，ΦBn和ΦBp值分别为0.095 eV和1.470 eV，故该异质结形成n型肖特基接触(n-type Schottky contact, NSC)。

功函数的大小可以表示电子从材料表面逸出的难易，可通过下式计算：

WF=Evac-EF

(2)

式中：Evac和EF分别表示真空能级和费米能级。计算得到graphene、Janus WSSe单层和graphene/WSSe异质结的功函数分别为-4.279 eV、-5.578 eV和-4.176 eV。因此，graphene和Janus WSSe形成异质结时，graphene单层的电荷会转移到WSSe上。接着对电荷密度差分(charge density difference, CDD)进行计算来进一步验证上述结论。电荷密度差分是通过异质结的电荷减去graphene和Janus WSSe孤立单层的电荷来定义的，这可以由公式(3)表示：

Δρ=ρH-ρgraphene-ρWSSe

(3)

式中：ρH，ρgraphene和ρWSSe分别是graphene/WSSe异质结以及graphene和Janus WSSe单层的电荷密度。

图3(e)展示了graphene/WSSe异质结的电荷密度差分，其中红色和绿色区域分别表示电荷积累和耗散。由图可知，异质结中graphene中的部分电荷会向WSSe上转移，这对前面的结果进行了进一步的验证。此外，在图3(f)中展示了沿z方向的平面平均电荷密度差分，其中负值和正值分别表示电荷耗散和积累。同样得到该异质结中graphene层的部分电荷朝WSSe层转移的结论。因此，graphene/WSSe异质结中形成了内建电场，如图3(g)所示。异质结中从graphene指向WSSe的内建电场在界面处生成势垒，有利于电子扩散与漂移达到平衡。

图3 Graphene/WSSe 异质结。(a)～(c)能带结构；(d) TDOS和PDOS；(e)三维电荷密度差分，等值面为0.001 5 e·Å-3；(f)平面平均电荷密度差分；(g)内置电场的示意图；(h)接触类型的示意图Fig.3 Graphene/WSSe heterojuction. (a)～(c) Band structures； (d) TDOS and PDOS； (e) the three-dimensional CDD, the isosurface refers to isovalues of 0.001 5 e·Å-3； (f) the planar-averaged CDD; (g) schematic model of built-in electric field; (h) schematic model of contact types

图4为graphene/WSSe异质结的光吸收谱。如图4(a)所示，graphene/WSSe异质结的吸收系数可被视为graphene和WSSe单层的吸收系数的叠加。通过与Janus WSSe单层构建异质结，graphene单层对可见光的吸收能力有明显的提升。如图4(b)所示，graphene/WSSe异质结在可见光区的吸收系数可达到7.5×104cm-1，约为Janus WSSe吸收系数最大值的1.25倍，graphene吸收系数最大值的2.8倍。相比于graphene和WSSe单层，graphene/WSSe异质结太阳能效率更高，表明其在功能光电器件中的巨大应用前景。

图4 光吸收谱Fig.4 Optical absorption spectra

2.3 调节异质结层间距

从器件应用的角度来看，层间耦合是提高电子器件性能的有效途径。众所周知，通过调整层间距离，层间耦合可以有效地影响graphene/WSSe异质结的电子特性，故调整层间距可以被视为是改善二维graphene基异质结电子特性和SBH的有效方法。在实验中，可以通过利用纳米机械压力[35]、热退火[36]来调节异质结的层间距。图5(a)表示垂直应变下graphene/WSSe的结构示意图，其中向上和向下的箭头分别表示拉伸和压缩应变。根据图5(b)，结合能可以被视为层间距离(D)的函数，当异质结层间距为0.341 nm时，结合能具有最低值，验证了表1中的计算结果。

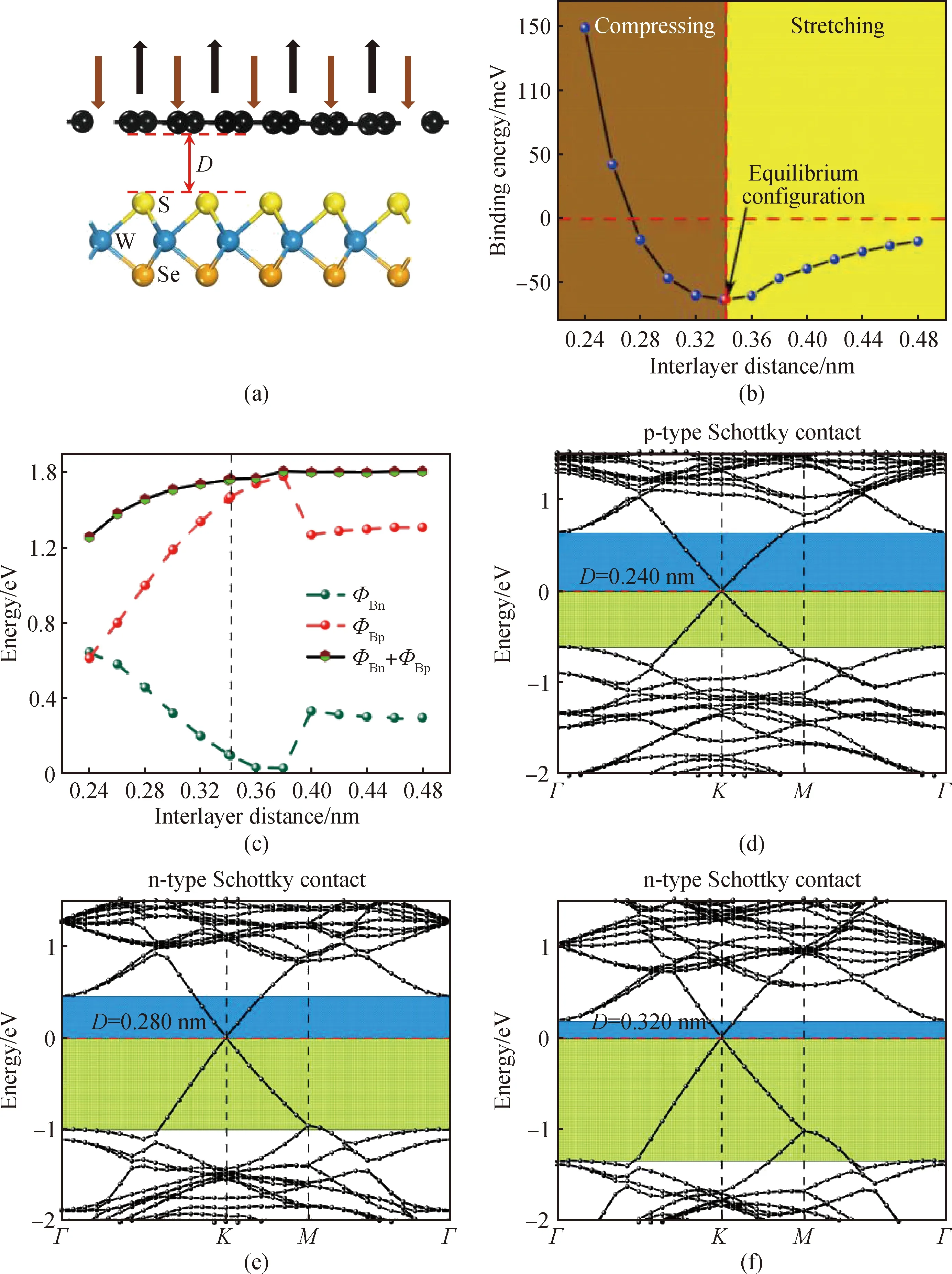
图5 z方向垂直应变下graphene/WSSe。(a)模型示意图；(b)～(c) Eb和SBH的变化趋势；(d)～(j)能带结构；(k) graphene/WSSe中graphene的掺杂Fig.5 Graphene/WSSe under vertical strain in the z-direction. (a) Schematic model； (b)～(c) change trend of SBH and Eb； (d)～(j) band structures； (k) doping of graphene in graphene/WSSe

图5(c)展示了不同层间距下graphene/WSSe的SBH的变化趋势。正如前面提及的，当D为0.341 nm时，ΦBn和ΦBp分别为0.095 eV和1.470 eV，此时异质结形成了NSC。根据图5(d)～(j)可知，随着D从0.341 nm降低至0.240 nm，ΦBn表现出逐渐增加的趋势，而ΦBp逐渐降低。当D达到0.240 nm时，ΦBp小于ΦBn，即0.615 eV<0.643 eV，表明在异质结界面处从NSC转变到p型肖特基接触(p-type Schottky contact, PSC)。根据图5(c)，通过将D从0.341 nm增加到0.380 nm，ΦBn由0.095 eV减少到0.026 eV，同时ΦBp从1.470 eV增加到1.580 eV，这意味着NSC特征得以保留。值得一提的是，当D=0.380 nm时，ΦBn非常接近0 eV，这意味着容易发生从NSC到欧姆接触的转变。当D从0.380 nm增加到0.400 nm时，ΦBn和ΦBp分别显示出急剧增加和减少的趋势，同时狄拉克锥在费米能级上方移动。而当D由0.400 nm增加到0.480 nm，NSC始终被保留下来。

值得注意的是，基于graphene基异质结中graphene的狄拉克锥位置会受垂直应变和外部电场控制。根据图5(k)可知，若电子从WSSe转移到graphene部分，graphene的狄拉克锥尖会移动到费米能级下方，这被定义为电子掺杂，即e掺杂。相反，电子从graphene转移到WSSe单层，graphene的狄拉克锥尖会移动到费米能级上方，这被定义为空穴掺杂，即h掺杂。狄拉克锥相对于费米能级的位移(ED)可表示为：ΔED=ED-EF。掺杂graphene的电荷载流子(电子或空穴)密度(Nh/e)可以通过公式(4)[37]获得：

(4)

根据图5(h)～(j)，当D从0.400 nm增加到0.480 nm时，狄拉克锥尖比费米能级高大约0.338 eV。根据电荷密度差分的分析，这种现象表明电子从graphene转移到WSSe部分。此外，当D从0.400 nm增加到0.480 nm时，空穴掺杂(Nh)的载流子密度为8.39×1012cm-2。

2.4 施加外部电场

外部电场也被认为是改善范德瓦耳斯异质结电子特性的有利方法[38]。本部分通过沿z方向向graphene/WSSe施加垂直电场来研究外部电场对其界面性质的影响。从WSSe到graphene的方向被定义为电场正方向，如图6(a)所示。由图6(b)可知，正负外电场都能将graphene/WSSe异质结界面处从NSC转变到PSC。在-0.3 V·Å-1的外电场下，graphene/WSSe的ΦBp和ΦBn分别为0.863 eV和0.662 eV，表明NSC在界面处形成。在-0.4 V·Å-1的外电场下，在异质结界面形成PSC，ΦBp和ΦBn分别为0.665 eV和0.863 eV。另一方面，正的外电场使得ΦBn和ΦBp分别呈现逐渐增加和减少的趋势。通过将外电场从0.1 V·Å-1提高到0.2 V·Å-1，ΦBp从1.320 eV降低到0.569 eV，同时ΦBn从0.173 eV增加到0.915 eV，异质结界面从NSC变为PSC。

图6(c)～(h)显示了不同外电场下graphene/WSSe的能带结构。如图6(c)～(f)所示，随着负的电场不断增加，费米能级朝着Janus WSSe的价带方向移动，ΦBp和ΦBn分别呈现减小和增加的趋势。另外，正的外电场下的费米能级显示出与负外电场下类似的移动趋势，如图6(g)～(h)所示。由图可知，通过将外电场从0.1 V·Å-1提高到0.2 V·Å-1，ΔED从0.335 eV增加到1.280 eV，这表明graphene/WSSe的Nh从8.24×1012cm-2增加到1.20×1014cm-2。因此，外电场可被视为调节graphene/WSSe异质结界面接触类型和SBH的有效方法。应注意的是，可以通过栅极电压在实验中实现外部电场的应用[39]。

3 结 论

本文借助第一性原理计算探索了graphene/WSSe异质结的电子特性和界面接触。通过形成graphene/WSSe范德瓦耳斯异质结，可以很好地保留graphene和WSSe单层的固有电子特性。Graphene/WSSe异质结中graphene的带隙为7 meV，这意味着该异质结在纳米电子和光电子器件中具有很好的应用前景。在可见光范围内，graphene/WSSe的吸收系数达到7.5×104cm-1，相比于WSSe和graphene单层，异质结表现出增强的可见光吸收能力。在平衡层间距下，异质结形成NSC，ΦBn和ΦBp分别为0.095 eV和1.470 eV。对于graphene基范德瓦耳斯异质结，层间距和外部电场被视为调节graphene狄拉克锥位置的两种有效策略。与层间距相比，外部电场对于graphene的载流子密度具有更宽的调节范围。向graphene/WSSe施加0.2 V·Å-1的外电场时，graphene最高载流子密度可以达到1.20×1014cm-2。这些计算结果对graphene/WSSe异质结电子器件的设计提供了理论依据。