向量自回归模型在慢性阻塞性肺疾病患病率预测中的应用研究
2022-02-01窦一峰王富彪贾新亮赵一犇吕劲松
窦一峰,王富彪,贾新亮,赵一犇,吕劲松
天津市宝坻区人民医院,天津 301800
慢性阻塞性肺疾病(chronic obstructive pulmonary disease,COPD)是包括慢性支气管炎、肺气肿等肺通气病理受阻的一组疾病,严重危害人类健康[1]。COPD 居全球死亡原因的第4位,世界卫生组织(WTO)预计到2030年,COPD 将升至第3 位[2-3]。由于COPD 晚期预后差,严重影响患者的劳动能力和生活质量,给整个家庭带来巨大的经济负担[4]。针对COPD患病率的预测,目前参考文献中主要采用统计学中的假设检验进行研究,但运用向量自回归模型(vector autoregression model,VAR)进行预测的文献较少。同时,向量自回归是基于数据的统计性质建立模型,它把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型,从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型,具有不用区分内生变量和外生变量,是一种无约束模型。基于以上两点,本文采用VAR探究建立天津市COPD患病率与气象因素之间的动态数量关系并进行预测,以期为更好地对该疾病的预防和控制提供新的参考依据。
1 资料与方法
1.1 一般资料
本文中COPD 的患病率数据主要来源于天津市疾病预防控制中心收集的全死因监测数据,时间周期为2000—2016年。按照《国际疾病分类》,周期为2000—2002年时采用ICD-9编码,2003—2016年采用ICD-10编码[5-6]。考虑到目前死因登记报告中绝大多数的未特指的肺源性心脏病都是由慢性支气管炎、肺气肿引起的,极少数才是由肺动脉栓塞、原发性肺动脉高压等引起的肺源性心脏病,因此本文也将这类疾病划归为COPD来统计分析[7]。本文的数据由天津市各医院统一进行网络直报,通过层级质检和抽样复核相结合的方式对数据的可靠性和一致性进行质量控制,保证了数据的有效性和准确性。
1.2 方法
本文主要应用EViews 10.0 软件对数据进行处理和分析,在建模准备阶段主要采用描述性统计分析和平稳性检验对数据进行初步感知,在模型建立与预测阶段主要采用VAR[8-10]进行建模和预测,并采用均方根误差(root mean square error,RMSE),平均绝对误差(mean absolute error,MAE),平均绝对百分比误差(mean absolute percentage error,MAPE) 和希尔不等式系数(thiel inequality coefficient,TIC)对预测效果进行评价。
VAR的理论基础在于数据的统计性质,通过将系统中每个内生变量作为所有内生变量的滞后期的结果来进行建模,因而使得由最初的单变量自回归模型向多元化序列变量自回归模型演变,完成从一元到VAR 的升级[11]。VAR对于各模块的系数关注不敏感,这是由于改模型中系数矩阵特别多的原因,所以很难通过分析模型系数估计值来分析模型所显示出的结果和意义。本研究主要通过关注特征根检验等前提条件[12],能够比较全面的反应各个变量之间动态影响的IRF脉冲响应函数[13],将系统内一个变量的方差分解到各个扰动项上的方差分解步骤[14],来对模型进行分析。
VAR(p) 模型的数学表达式如下:
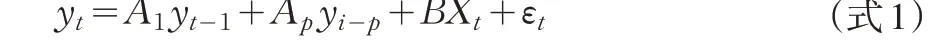
其中,yt代表n维内生变量向量,Xt代表d维外生变量向量,p 是滞后阶数,样本个数为N。n×n 维矩阵A1,…,Ap和B 是要被估计的系数矩阵。是n 维扰动向量,也称为冲击向量或者抖动,因为它没有结构性的含义,被称为简化形式的冲击向量。
2 结果
2.1 数据描述性统计
本文收集了2000—2016年共计17年的COPD患病率数据,整体来看该疾病患病率为4.34%~6.23%,Z 统计量为329.98,P 值小于0.001,APC 值为2.26%,数据呈现出明显的上升趋势,见表1。

表1 天津市2000—2016年COPD患病率和气象数据描述性分析
2.2 平稳性检验
时间序列的平稳性决定了能否进行VAR 模型分析,这 里 采 用 单 位 根 检 验[15](augmented dickey-fuller,ADF)对各个变量进行平稳性检验。为了克服异方差和消除量纲的影响,本文对数据先进行对数化处理。由表2可知,在的条件下,各序列0 阶差分是平稳的,1 阶差分也是平稳的。
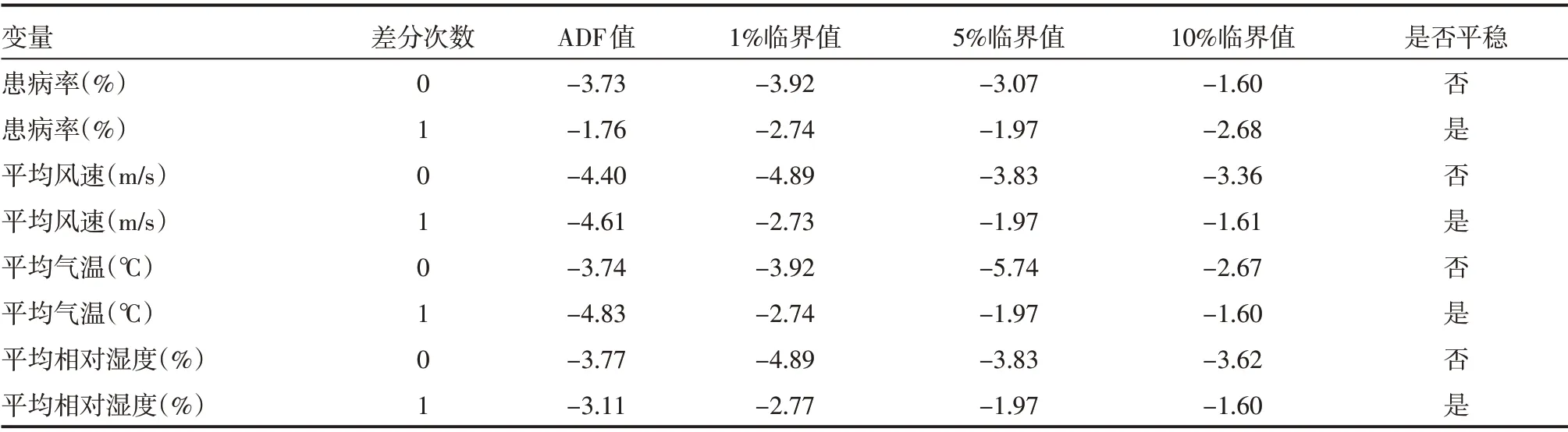
表2 天津市2000—2016年COPD患病率和气象数据平稳性检验结果
2.3 VAR模型的建立
本文考虑到VAR 模型是无约束模型,因此设定包含COPD患病率和平均气温、平均风速等指标的VAR模型如式(2)所示:
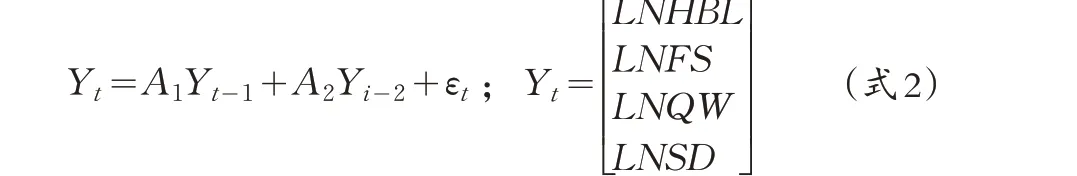
采用模型滞后阶数确定准则,以AIC和SC最小化为判定依据确定滞后阶数为2,此时的AIC=-9.418 6,SC=-8.993 7。VAR模型结果见表3,其中模型拟合优度检验结果中R方为0.999 8,调整后的R方为0.999 6,说明模型拟合效果较优,F 统计量为4 693.735 0,对应的P=0.000 0<0.01。同时根据COPD 患病率作为因变量的格兰杰因果检验结果可知,整体的卡方值为19.607 7,P=0.003 3<0.05,说明各气象因素均为COPD 患病率的格兰杰原因,表明建立的VAR模型是合理有效的。
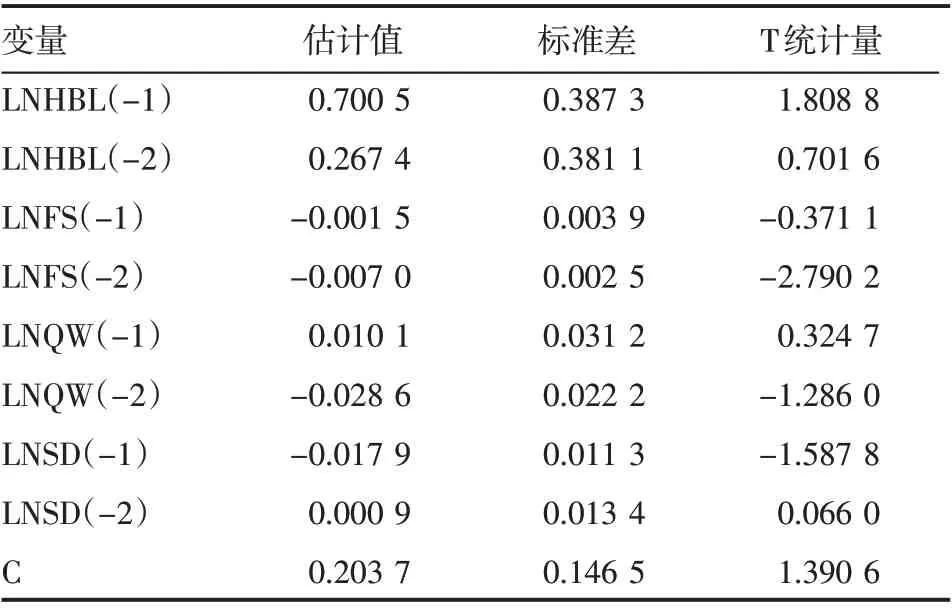
表3 天津市2000—2016年COPD患病率和气象数据VAR模型结果
2.4 AR特征根检验
随着时间的推进,将一个脉冲作用在VAR中每个方程的信息上,发现该次冲击的影响会逐渐减退直至消失,则说明该系统是稳定的,否则是不稳定的。对于VAR模型来说,系统的稳定性是进行脉冲响应函数、方差分解等分析的基础,而衡量VAR是否稳定的方式就是借助AR特征根检验。本文中由4个内生变量且滞后期为2,因此会产生8个特征根,所建立的VAR模型的所有特征根的倒数的模均小于1,即根据图1 所示,所有点都位于单位圆内,说明本文建立的VAR模型是稳定的。
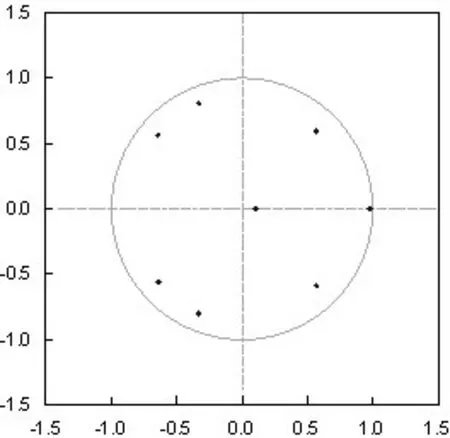
图1 AR特征根的倒数的模的单位圆结果
2.5 脉冲响应函数分析
脉冲响应函数分析是一类描述系统中每一个内生变量的冲击对其他内生变量所带来的影响的分析方法。如图2所示,LNHBL受自身冲击后产生小幅波动,随后开始逐步下降直至平稳状态,总体表现为正向长期影响;LNHBL受LNQW 冲击后呈现正负向交替波动影响;LNHBL 受LNFS和LNSD 的冲击后,均表现为负向影响,到第5 期影响达到最高点,随后逐渐减弱,直至到长期稳定的趋势。图中实线表示的是变量受冲击后的走势情况,两侧的虚线表示走势的两倍标准误差。
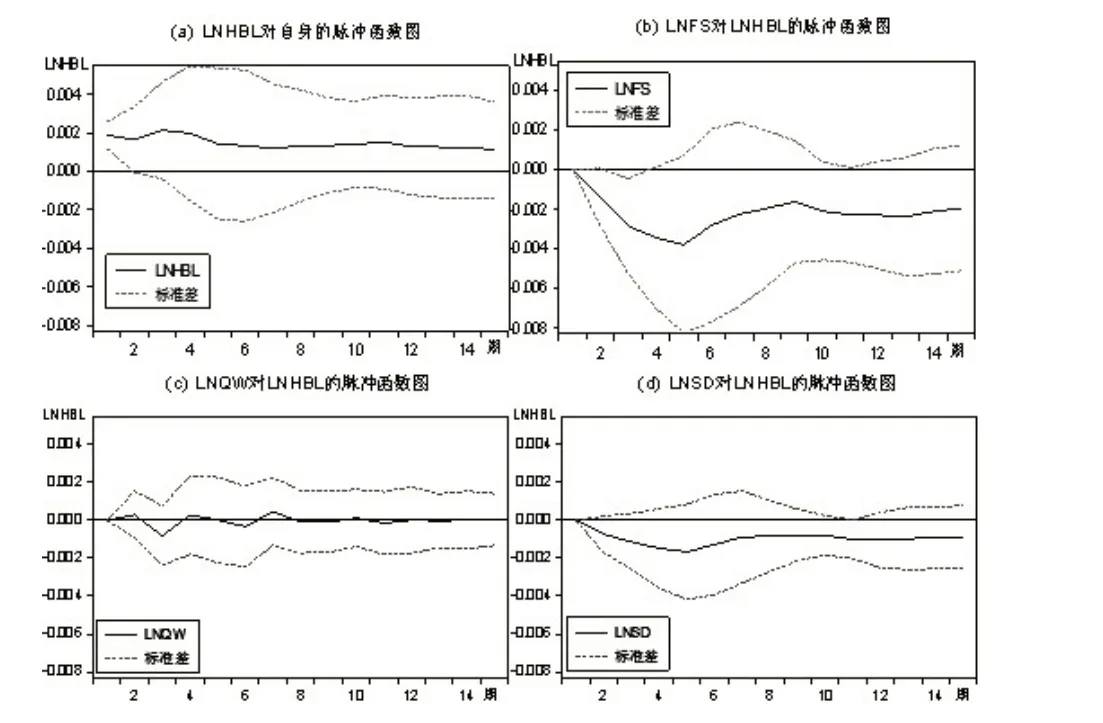
图2 VAR模型脉冲响应函数结果
2.6 方差分解分析
方差分解提供的是关于每个扰动因素影响VAR模型内各个变量的相对程度的信息,即一个冲击要素的方差能由其他随机扰动项解释多少。表4 给出了COPD 患病率的变动方差由自身和气象因素导致的结果,COPD 患病率变化贡献率最大的影响因素是其自身的变化,主要表现为逐年递减趋势,从第5期开始下降幅度变缓趋于平稳,直至第15期贡献率仍超过24%,风速的变化对COPD患病率的贡献影响逐年增高,到第6 期后期逐渐趋于平稳,最终达62.694 5%,其他因素的贡献率均不超过12%。由图3可以看出,由各个气象因素变动解释的部分逐年增加,说明受气象因素影响较明显。
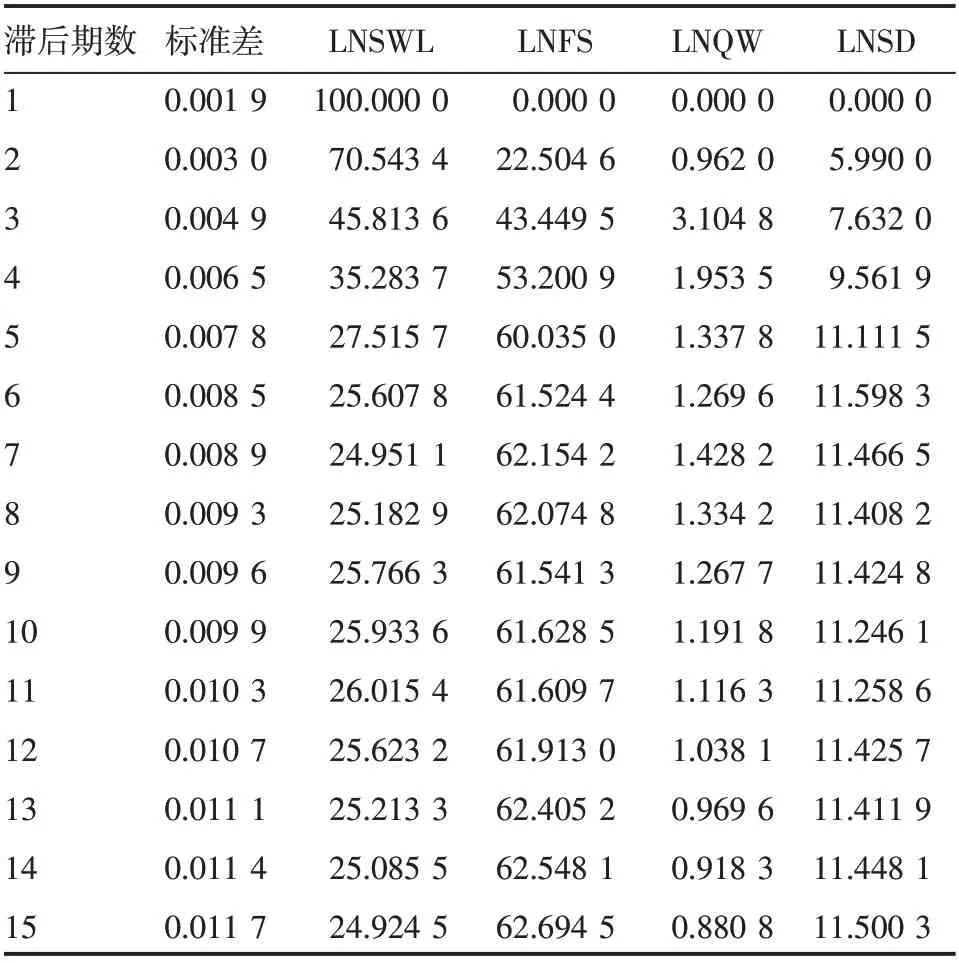
表4 方差分解结果
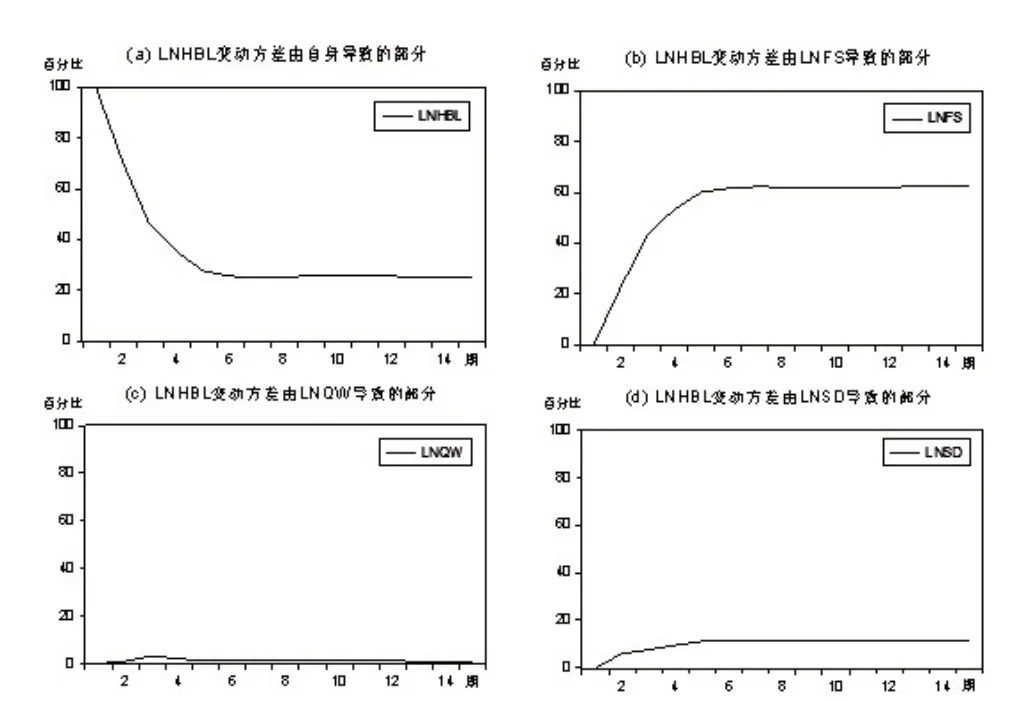
图3 方差分解趋势
2.7 VAR模型预测
基于本文所研究的是COPD 患病率和气象因素之间的关系,因此选取COPD患病率为被解释变量,得到VAR模型表达式如式(3)所示。

根据上述公式采用动态预测法对2017—2021 年的COPD 发病率进行预测,采用RMSE、MAE、MAPE 和TIC进行效果评价,如果RMSE、MAE、MAPE 介于0~5 之间,TIC 在0~1 之间,则说明预测结果较好,评价指标值越小,则说明模型的预测精度越高。由表5可知,各个指标均在可接受的范围内,说明模型可以较好地预测未来5年的COPD患病率。
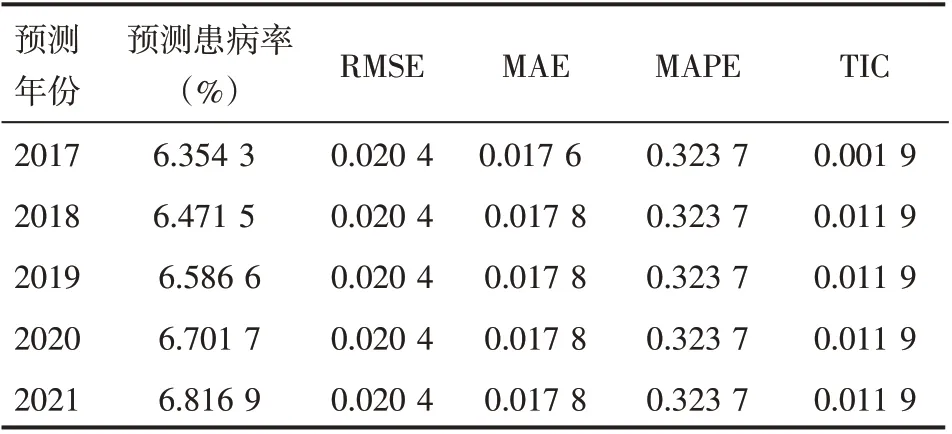
表5 VAR模型预测COPD患病率结果
3 讨论
从所建立的VAR模型得到的脉冲响应函数结果来看,气温对于COPD的发病表现为正负交替影响,说明气温的骤增和骤减均会使COPD发病的风险增大,分析原因可能是天津地处华北地区,四季较为分明,尤其冬天早晚温差较大,对支气管和心肺功能会有较大影响。通过方差分解结果可知,风速和湿度对于COPD 发病率的贡献度较高,分析原因可能是由于空气中湿度增加以及风速的增大,病毒繁殖和活动能力增强,也有利于污染物的扩散,从而增加了患病的风险,这也与相关文献研究结果一致[15]。
本研究通过对COPD患病率和气象因素数据建立VAR模型来预测未来COPD 患病率的发生情况,根据结果来看,所建立的VAR模型的稳定性和拟合效果均较好,模型的预测结果评价指标也说明该模型可以较好的对未来COPD患病率进行预测,其RMSE、MAE、MAPE和希尔不等式系数均较小,说明利用COPD患病率和气象资料数据所建立的天津市COPD患病率预测的VAR模型的适用性较好,可操作性强,进一步说明运用数学模型的思想来科学动态的对COPD发病率进行研究是可行的。虽然整体上各气象因素可作为模型预测的变量,但是各气象因素是否真正对COPD 患病率具有影响作用仍有待进一步研究。未来,通过收集更多的特征信息和数据资料,提升数据的准确性和全面性,对于疾病患病率的预测可以从模型融合和信息融合的角度进行建模尝试,并根据统计和分类等多维度评价指标对模型进行评价分析。
