基于Jackknife互信息的高维非线性回归模型研究

张治飞, 段 谦, 刘乃嘉, 黄 磊*

(1.西南交通大学数学学院, 四川成都611756; 2.西南财经大学统计学院， 四川成都611137)

互信息(mutual information, MI)主要在计算机、信息技术和机器学习等领域具有应用广泛。例如，基于亲密度和吸引力的二分网络社区发现算法中MI作为划分的评价指标，即划分过程中MI越大，说明划分结果越好[1]；在图像处理研究中，MI作为图像配准的相似性测度函数，实现对遥感图像的配准，如基于改进型MI的遥感图像配准方法[2]。但目前MI在统计学变量选择领域的应用相对较少，所以本文将研究MI是否可作为变量选择的一种有效工具。

作为一种随机变量之间独立性的度量，MI具有严格的单调转换不变性。此外，MI在测量线性随机变量间以及非线性随机变量之间的相关性能力具有一致性。因此，MI可以作为随机变量之间相关性的一种重要度量。目前大部分对MI的估计，特别是对于连续数据，在很大程度上依赖于所涉及调优参数的选择，例如连续数据离散化过程中bins的数量、核密度估计(kernel density estimator，KDE)中的带宽以及k-近邻(k-nearest neighbor，kNN)估计器中的邻居数量等，因而，相应的估计量可能非常不稳定或有严重偏差，所以使用MI进行相应的研究时，研究效果也会受到MI估计量好坏的影响。为了估计量不受带宽选择的约束，Zeng等[3]提出基于刀切(Jackknife)方法的MI估计(JMI)。JMI完全由数据驱动，不会产生预先确定的调优参数，具有良好的统计特性。因此，基于其优良统计性质及简单易行的算法，本文将使用JMI对高维非线性模型的重要变量进行选择。

对于线性回归模型的变量选择问题，根据文献[4]，相应算法主要包括3类：第1种基于统计检验，如通过检验模型的残差平方和以及对变量进行t检验等选择变量，主要代表就是逐步回归和自动计量学(Autometrics)；第2种基于惩罚的最小二乘估计，即直接在一般线性回归模型的损失函数内部对参数施加约束来提高它们之间的稀疏性，例如岭回归和LASSO(最小绝对值收缩和选择算子)等；第3种就是筛选算法，此类算法并不是为了进行本质上的选择，而是根据重要性对变量进行排序，它的主要优点是，当变量数p远远大于样本量n，即p≫n的情况下，筛选方法更容易应用于此类问题，其中最具代表性的是Fan等[5]研究的确定独立筛选(SIS)。SIS是一种简单有效的方法，但由于SIS可能会遇到选择出弱相关变量(弱信噪比)的问题，因此Fan 等[5]对SIS进行改进，得到了迭代SIS，即ISIS。

目前已经有学者采用SIS进行变量选择的研究，如对癌症病人进行生存预测[6]，以及利用GSIS方法对心肌病数据进行变量选择，进而研究基因对于G蛋白耦联受体Ro1的影响[7]等。然而(I)SIS在最初提出时就仅对线性回归模型中的变量具备良好的选择能力，虽然(I)SIS已经扩展到广义线性回归模型中，并且也具有良好的变量选择效果，但同线性和广义线性回归模型相比，非线性回归模型和广义非线性回归模型存在参数估计、统计推断等问题，特别是非线性回归模型中的变量选择领域的统计研究仍然存在许多未解决的问题。

为了处理非线性回归模型中的变量选择问题，研究人员提出了一些有效可行的方法。Hall等[8]从经验似然观点出发，考虑不同边际效用后提出一种广义相关系数，它可以作为非线性相关的度量。Antoniadis 等[9]以及Yuan等[10]研究了选择分组变量的方法。Lin等[11]在变量数目固定的平滑样条方差分析中提出模型选择的成分选择与平滑算子(COSSO)方法。Ravikumar等[12]相继在高维非参数可加性模型中考虑变量选择，其中可加性成分的数量大于样本容量。Zhu等[13]开发了基于距离相关(DC-SIS)的SIS，此方法也可以对变量的边际重要性进行排序，利用DC-SIS来选择高维回归分析中的变量能较好地控制异常观测后的不良影响，且优于同类方法。Cui等[14]提出一种基于经验条件分布函数的边缘变量筛选方法的非参数加性模型。Mai等[15]采用融合的Kolmogorov滤波器来处理可变筛选问题。Wu等[16]将非负garotte和SIS相结合进行高维稀疏非线性回归模型的变量选择。

SIS方法即通过将皮尔逊相关系数作为线性相关的一种度量，利用计算所得的相关系数，以此对线性回归模型的变量进行排序筛选。但由于相关系数无法检测变量间的非线性关系，所以SIS并不能解决超高维稀疏非线性回归模型的变量筛选问题。本文运用SIS思想，将MI作为变量之间非线性关系的一种度量，即MI代替皮尔逊相关系数，并对变量的边际重要性进行排序，然后对非线性回归模型的变量进行选择。此研究思想简明直接，仅将原有对相关性的度量方式进行替换，研究超高维稀疏非线性回归模型的重要变量选择问题。又因MI的刀切估计量JMI具有良好的统计特性，本文将给出JMI与SIS相结合的算法，并通过模拟试验和实例分析，进一步展示所提方法的相合性，通过实例分析说明本文所提方法在解决超高维稀疏非线性回归模型中变量选择问题的可行性和实用性。

本文安排如下：第1章对JMI、(I)SIS进行简单叙述，并介绍SIS+JMI算法、ISIS(LASSO)+JMI算法；第2章通过模拟试验，对第1章所得算法的相合性进行验证；第3章展示ISIS(LASSO)+JMI算法在实例数据分析中的应用；第4章是结论。

1 互信息的估计以及重要变量选择方法

1.1 互信息的刀切估计

1.1.1 互信息定义

随机变量X=(X1,X2,…,XP)T与Y=(Y1,Y2,…,YQ)T，记fX、fY、fXY分别为随机变量X与Y的边缘概率密度函数以及联合概率密度函数。X与Y的互信息数学定义为

(1)

式(1)中的X与Y可以容易地扩展到其他类型的随机变量，它们可能没有密度函数，如离散型随机变量等。从定义可知MI总是非负的, 即MI(X,Y)≥0，当且仅当2个随机变量独立时等式成立。当2个随机变量之间的依赖性越弱时，MI越接近于0。为了能够对复杂依赖关系进行刻画，将MI作为描述随机变量间非线性关联的一种度量，可以对随机变量间的非线性相关性等问题进行研究。

1.1.2 互信息的刀切估计(JMI)

JMI是对以往MI的核密度估计方法的进一步改进，与 KDE方法的区别在于对其中4个带宽矩阵的设置。文献[3]通过基于独立测试的经验结论和理论推断，证明了最后4个带宽矩阵应该设置为相等的结论。所以Zeng等[3]在KDE的基础上将带宽矩阵设置相等后，利用刀切思想得到了MI的刀切估计量JMI。

随机变量X=(X1,X2,…,XP)T与Y=(Y1,Y2,…,YQ)T相互独立，对角带宽矩阵HX、HY、BX、BY分别为：

在对角矩阵A上，考虑核函数

KP是一个P维对称密度函数，

随机变量X、Y的观察值分别为xip,i=1,2,…,n,p=1,2,…,P、yiq,i=1,2,…,n,q=1,2,…,Q，则X、Y、X,Y的概率密度函数的KDE为：

MI的KDE估计为

(2)

在式(2)的基础上对MI采用刀切法以及引用copula函数，得到JMI。

利用MI在严格单调转换下不变的性质以及概率分布函数服从0到1的均匀分布的特点，得：

V=(V1,V2,…,VQ)T=(FY1Y1,FY2Y2,…,FYQ(YQ))T。

式中FXp(x)(p=1,2,…,P)，FYq(y)(q=1,2,…,Q)分别为Xp、Yq的概率分布函数，所以U、V的各分量服从(0,1)的均匀分布，且满足MIU,V=MI(X,Y)。

记cU(u)、cV(v)、cUV(u,v)分别为U、V、(U,V)的copula密度函数。U、V的观察值记为

同时利用概率分布函数对其表示为

式中FXp,n(p=1,2,…,P)、FYq,n(q=1,2,…,Q)分别为X、Y各分量的经验分布函数。

对U、V的边缘以及联合copula密度函数进行核估计，得到copula密度函数在刀切法下的核函数估计为：

根据文献[3]，将上述4个带宽矩阵设置为HX=HY=BX=BY=diag(h2,h2,…,h2)。得到JMI的数学定义为：

(3)

(4)

JMI具有3个特点：第一，完全是由数据驱动的，不会产生预先确定的其他调优参数。第二，具有良好的统计特性，如自动纠偏和独立性检验的较高的局部检验功效。关于局部检验功效的详细介绍，请参看文献[17]。第三，通过采用唯一的最大值，可使JMI(X,Y)在数值上保持稳定。

接下来对SIS、ISIS进行简单概述，并论述这2种算法的实现过程。

1.2 变量选择方法

1.2.1 确定独立筛选SIS定义

解释变量X=(X1,X2,…,Xp)，响应变量Y，X的观察值x=(x1,x2,…,xp)n×p，Y的观察值为y=(y1,y2,…,yn)T，参数向量为β=(β1,β2,…,βm)T。此时y=(y1,y2,…,yn)T为x中某m个变量的线性组合，

(5)

式中ε=(1,2,…,n)T为随机误差项。当p≫n时，根据文献[5]中SIS的定义，计算所有xi(i=1,2,…,p)与y之间的相关系数

ρi=cory,xi，i=1,2,…,p,

并将ρ1,ρ2,…,ρp按照绝对值从大到小的顺序进行排序后记为ρp,ρ(p-1),…,ρ(1)，最后在给定的γ∈(0,1)下，筛选出个数少于n的前d=γn个解释变量，组成筛选变量集Mγ={Xi|1≤i≤p：|ρi|≥|ρ(d)|}，将包含m个真实变量的变量集记为M0。

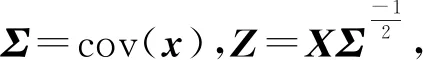
(6)

根据文献[5]，有如下正则条件：

条件1在p>n前提下，lnp=Onξ，ξ∈(0,1-2κ)，其中κ由条件3给定。

条件2Z具有球面对称分布以及集中属性，同时，ε～N(0,σ2)。

条件3varY=O(1)，存在κ≥0，c2，c3>0,有

条件4 存在τ≥0，c4>0，有λmaxΣ≤c4nτ。

在上述正则条件下，若2κ+τ<1，存在θ<1-2κ-τ，当存在常数c>0,γ～cn-θ时，存在常数C>0，SIS具有如下的确定筛选性(sure screening property)性质，

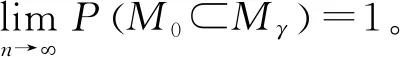
1.2.2 基于LASSO下的ISIS

由于SIS仅利用xi(i=1,2,…,p)与y之间的边缘相关系数，所以SIS具有3个潜在的问题：第一，一些与重要解释变量xi高度相关的不重要解释变量xj，比其他与响应变量y相关性相对较弱的重要解释变量xl更容易被SIS选择；第二，SIS不能选择与响应变量y联合相关但边缘不相关的重要解释变量xi，因此xi不能进入估计模型；第三，解释变量xi与xj(i≠j)之间的共线性问题给变量选择增加了难度[5]。

为了解决上述SIS的3个问题，Fan 等[5]相继提出迭代SIS，即ISIS算法。对于一个超高维稀疏线性回归模型，ISIS(LASSO)利用SIS对全变量集A进行筛选后得到变量集A1，再对A1通过LASSO回归进行变量选择得到新的变量集B1并得到这些变量的相应残差，然后在A/B1的变量集上，以B1中所得的残差作为新的响应变量，重复进行上述的SIS与LASSO步骤进行变量选择，最后将每一步经LASSO筛选得到的不相交变量集Bi进行合并，直到最后达到确定的变量个数为止。

ISIS(LASSO)能够很好地解决SIS仅利用边缘的相关信息所带来的问题，效果比SIS有了很大的提升。SIS与ISIS(LASSO)已被推广到高维空间中稀疏广义线性模型中的变量筛选，然而仅利用皮尔逊相关系数不能够解决在高维稀疏非线性回归模型的变量筛选问题。

利用SIS、ISIS(LASSO)方法的思想，以及MI可作为变量间非线性关联度量的特点，本文将原有的皮尔逊相关系数替换为计算效率更高且稳定的JMI，简记为SIS+JMI与ISIS(LASSO)+JMI算法。接下来将详细介绍SIS+JMI与ISIS(LASSO)+JMI算法。

1.3 基于JMI与(I)SIS的变量选择算法

1)SIS+JMI算法：

Step1对样本X=(x1,x2,…,xp)n×p和样本y=(y1,y2,…,yn)T，分别计算出JMI(y,xi)(i=1,2,…,p)。

Step2对Step1计算出的JMI(y,xi)(i=1,2,…,p)结果进行降序排列。

Step3对Step2排序后的JMI值，将前n-1个JMI所对应的解释变量进行输出作为最后的筛选变量集。

2)ISIS(LASSO)+JMI算法：

Step1样本X=(x1,x2,…,xp)n×p和样本y=(y1,y2,…,yn)T，利用SIS+JMI筛选得到包含变量个数为n-1的变量集A1。

Step2对A1进行LASSO回归得到变量集B1以及B1中的残差e1=(e11,e12,…,e1n)T。

Step3将Step2中的残差e1作为新的响应变量，然后在X/B1变量集上利用SIS+JMI算法得到变量集A2，重复Step2得到与B1不相交的变量集B2以及残差e2。

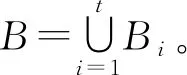
下一章将利用SIS、ISIS(LASSO)、SIS+JMI与ISIS(LASSO)+JMI算法，对高维空间中响应变量为二元变量型的数据类型进行模拟试验，以及解释变量与响应变量呈线性关系、非线性关系的数据类型分别进行模拟试验，最后得到个数为n-1的解释变量集。通过与经典SIS以及ISIS(LASSO)的筛选结果进行比较，验证SIS+JMI、ISIS(LASSO)+JMI具有确定筛选性。

2 统计模拟试验

本章通过R语言，使用第1章提出的JMI+(I)SIS算法，进行模拟试验一与模拟试验二，以此说明所提算法的确定筛选性。

2.1 统计模拟试验一

在本试验中，回归系数分别为θ1=(5,5,5)T(Model.1)和θ2=(2,4,6)T(Model.2)的2个Logistic回归模型：

式中1≤i≤n。响应变量y=(y1,…,yn)T由如下示性函数确定：

式中ρ～U(0,1)。在模拟过程中，设置p-3个与y无关的解释变量样本为X′=(x4,x5,…,xp)n×(p-3)，得到设计矩阵X～Np(0,I)。

在试验过程中发现，针对响应变量为0-1型的情型下，仅采用JMI对原ISIS(LASSO)进行改进后的效果提升较小，因此同时考虑线性与非线性下的相关度量，我们对解释变量xi(i=1,2,…,p)与响应变量y的JMI(xi,y)和corxi,y进行计算。为综合利用JMI(xi,y)对非线性相关性度量以及corxi,y对线性相关性度量的优势，同时将所得的JMIxi,y与cor(xi,y)结果进行求和取平均，对所得结果进行降序排列，最后将前n-1个对应的解释变量作为最终识别得到的重要变量，将此简记为SIS+JMI(N)算法。同理,对于本文提出的ISIS(LASSO)+JMI也利用SIS+JMI(N)算法改进，简记为ISIS(LASSO)+JMI(N)算法。

本文取样本量为n=20，50，70，设置模型变量个数p=100，1 000，并进行200次蒙特卡罗模拟。本文记录了模拟过程中Model.1和Model.2的解释变量x1、x2、x3包含于被选变量集合的频率。其中，LASSO中的惩罚参数λ通过3折交叉验证选出。模拟结果如表1、表2所示。

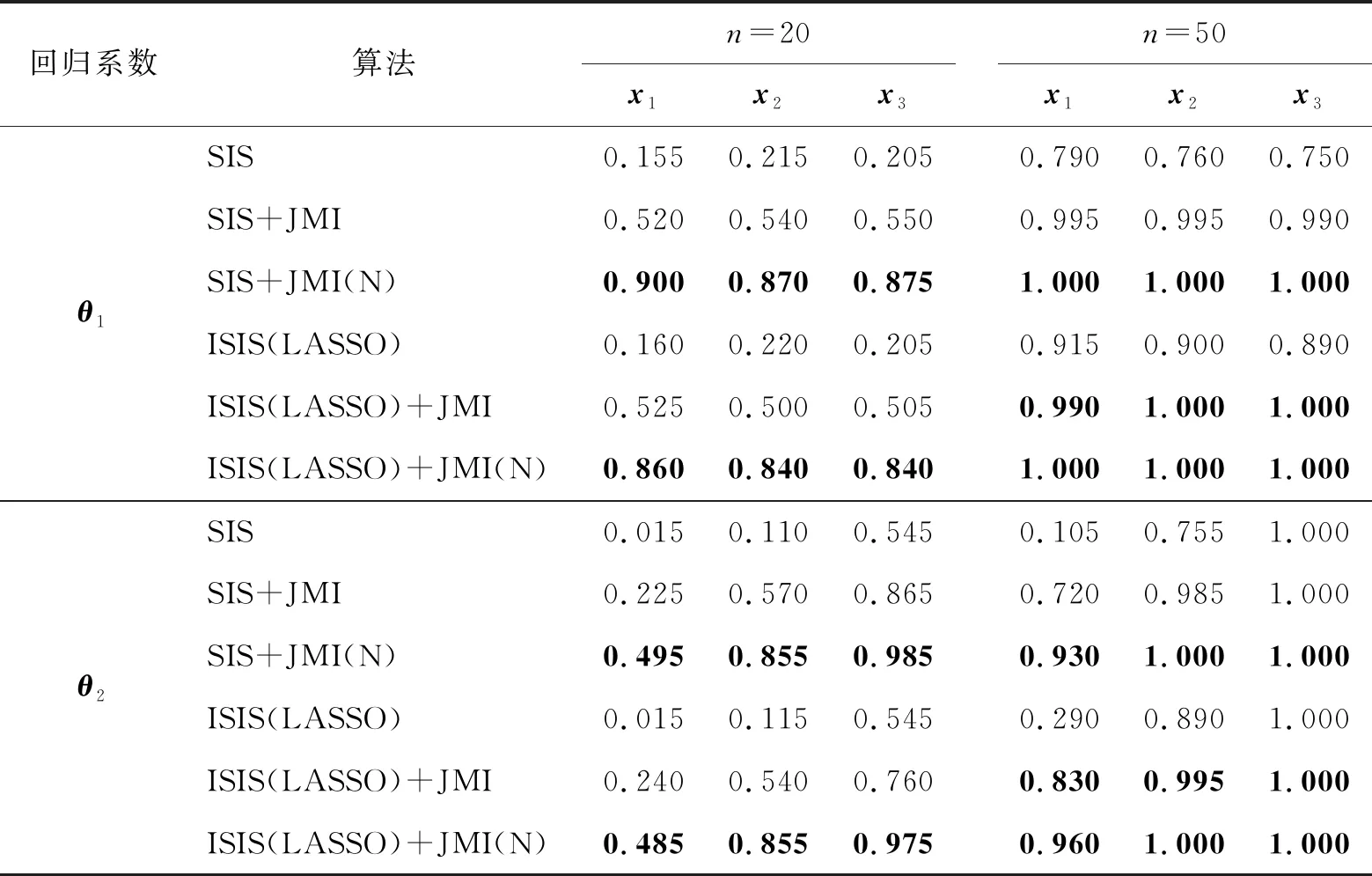
表1 p=100, n=20, 50下Model.1和Model.2的变量选择结果

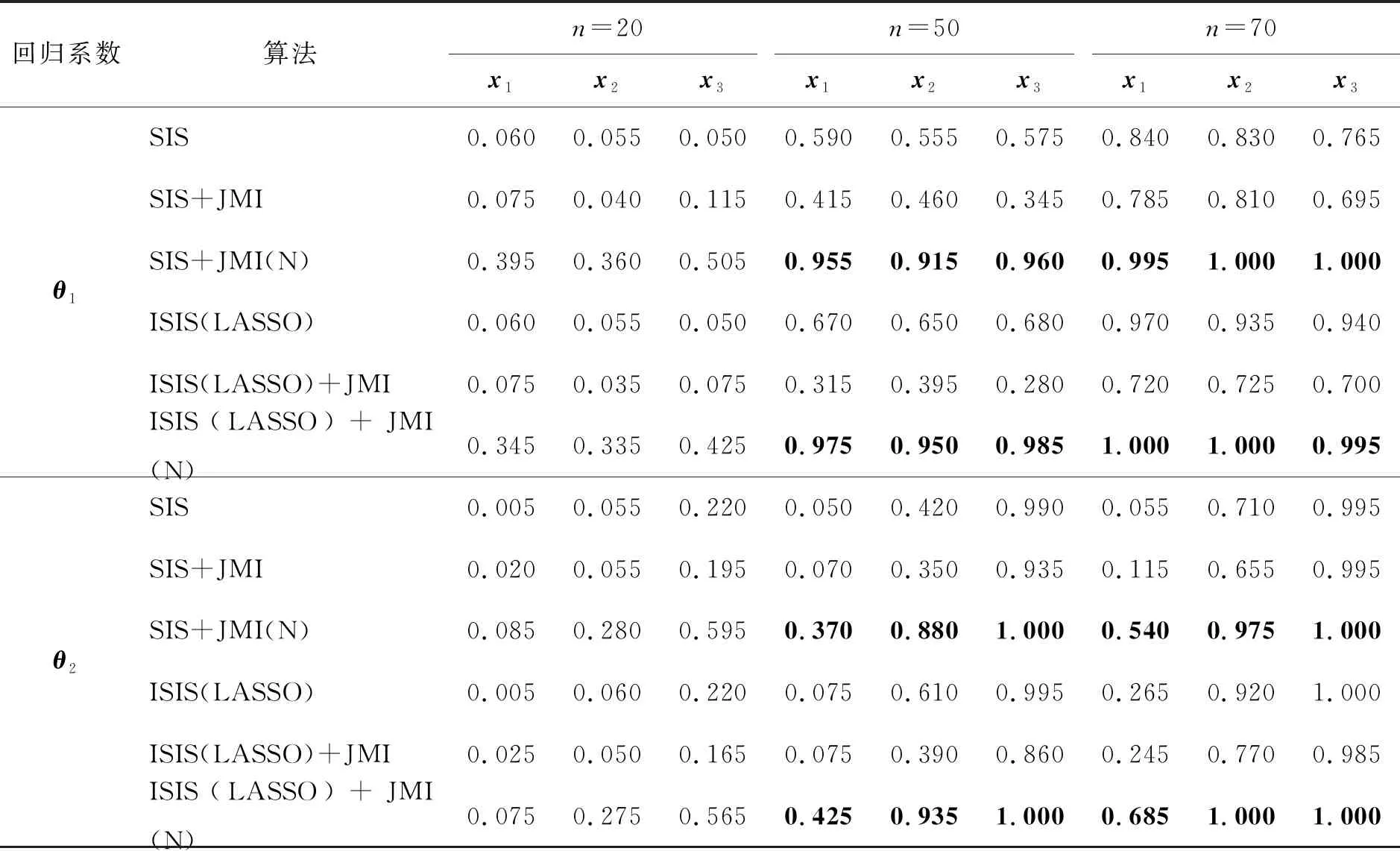
表2 p=1 000, n=20, 50, 70下Model.1和Model.2的变量选择结果

从上述结果发现，在不同的n、p下对于参数θ1、θ2，发现6种方法在相同p下，随着n的变大，最后的被识别频率都会趋于1，即随着n变大，所有真实变量包含于被选变量集合是依概率收敛到1的。此外，JMI与SIS的简单结合算法与经典SIS相比效果不好，而将所提方法进行改进后，即SIS+JMI(N)、ISIS(LASSO)+JMI(N)可对经典SIS进行改进，其中ISIS(LASSO)+JMI(N)试验效果在6种方法中最好。对于x1、x2、x3具有不同贡献度，即在参数θ2的结果中发现，此时贡献度的设置对最终的结果产生影响，即具有越大的贡献度的解释变量被选中的频率越大，如在Model.2中具有最大贡献度的x3被选择的频率比具有最小贡献度的x1大，且差距明显。

2.2 统计模拟试验二

采用模拟试验一中的解释变量X，并设置4种真实模型：

Model.3yi=5x1i+5x2i+5x3i+εi,

Model.4yi=3cosx1i+5x2i+5x3i+εi,

其中随机误差项ε～N(0,1)。取样本量为n=20，50，70，设置模型变量个数p=100，1 000，进行200次蒙特卡罗模拟。同时记录了模拟过程中Model.3至Model.6中解释变量x1、x2、x3包含于被选择变量集合的频率。其中，LASSO中的惩罚参数λ仍然通过3折交叉验证选出。模拟结果如表3、表4所示。

从表3、表4的结果发现，本文所提的将JMI与SIS相结合的算法，在非线性回归模型中保持了对线性变量的筛选能力，同时也具备了对重要非线性变量的筛选能力且效果理想。其中4种模型的x1、x2、x3筛选效果都在ISIS(LASSO)+JMI下最好。在相同的p下，对于采用的4种变量选择方法，都使x1、x2、x3被选中的频率随着n的增大而增大，即都随着n变大，识别所有真实变量的概率能依概率收敛到1。

表3 p=100, n=20, 50 下Model.3至Model.6的变量选择结果

表4 p=1 000, n=20, 50, 70下Model.3至Model.6的变量选择结果

3 实例分析

在第2章中通过模拟试验一、二的结果分析可知，对于数据类型为二元变量型的响应变量，ISIS(LASSO)+JMI(N)算法对此类数据的变量选择效果最好。同样，对于解释变量与响应变量间存在非线性关系的数据类型，ISIS(LASSO)+JMI算法的筛选效果最好。所以本章将采用此2种算法分别进行相应的实例分析，以说明所提方法的实用性。

3.1 实例分析一(leukemia数据)

数据来源于Golub等[18]得到的白血病数据集，其中响应变量y为0-1型变量，y=0表示未患白血病，y=1表示患白血病。此数据集包含样本量n=72，解释变量数p=7 129，n≪p属于超高维空间。根据y的数据类型，使用ISIS(LASSO)+JMI(N)方法筛选得到71个解释变量，然后采用朴素贝叶斯分类器分别计算出解释变量数从1至71累积增加时分类结果的AUC值和错误率，以此作为将变量数进一步缩减的标准。对这71个解释变量中的前5个解释变量做描述性统计，结果如表5所示。

从表5的最小值与最大值可以发现，数据的波动范围很大，且中位数、均值与3/4分位数都与最大值之间具有较大的差距。同理，均值与中位数之间的差距也很大。

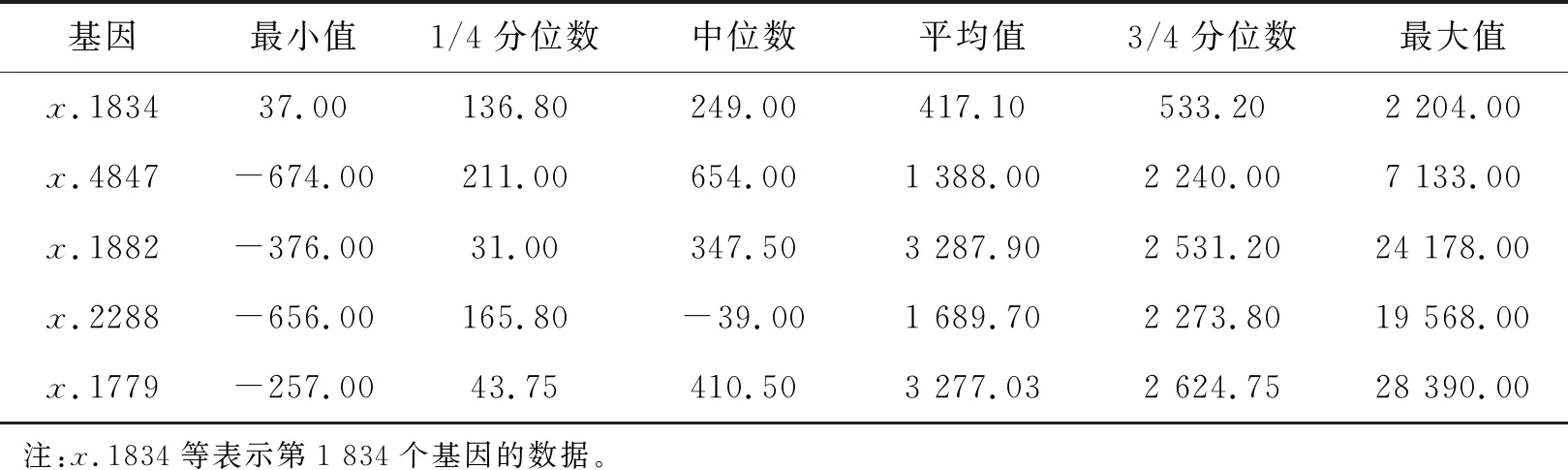
表5 Leukemia数据变量选择后前5个解释变量的描述性统计

对leukemia数据随机选取70%作为训练集，30%作为测试集，在重复随机选取10次后，得到10组不同的训练集以及测试集。在每组训练集中采用ISIS(LASSO)+JMI(N)选择出的71个解释变量，分别计算出变量数从1至71之间的AUC值以及分类错误率，最后，由10个随机分组后所得的AUC值以及错误率的平均值，画出平均AUC值与平均错误率如图1所示。

图1 AUC值与错误率随变量数变化关系

从图1发现所得的AUC值很高，错误率也挺低。发现只有第1个被筛选出的解释变量时，通过计算AUC值为0.989 583 3，错误率为0.1，说明筛选出来的第1个解释变量已经完全可以进行分类，所以考虑当AUC值首先达到0.99时的变量即作为最后筛选出来的变量集，接下来在验证集中进行分类。

在上述随机10次分组所得的测试集中，采用所筛选出来的前2个解释变量在朴素贝叶斯分类器下进行分类，并计算此时的AUC平均值以及分类错误率平均值,结果如表6所示。

表6 Leukemia数据经变量选择后的分类结果

从表6可知，由ISIS(LASSO)+JMI(N)方法选择得到71个变量中，采用前2个解释变量进行分析时，训练集中分类错误率为0.02，测试集中错误率为0.059 090 91，其AUC值也是达到了0.99以上，所以在此实例分析中，能说明所提方法在此类数据类型下具有良好的识别效果。

3.2 实例分析二(mRNA数据)

数据来源于Rabani等[19]实验得到的mRNA数据集，该数据利用4-硫脲嘧啶(4sU)对RNA进行短时间的代谢标记，从整体RNA中区分出最新转录的RNA，从而获得RNA转录率的直接测量结果。他们检测了254个代表性特征基因在小鼠树突状细胞对脂多糖(LPS)反应过程中的RNA-total和RNA-4sU的表达。每个基因有13个测量值，在LPS刺激后的前3 h内每隔15 min测量1次。由文献[19]可知有44个基因被鉴定出具有不同的降解率。根据文献[16]，将响应变量设定为来自这44个基因的其中一个基因的RNA-4sU表达，解释变量则是所有254个基因的RNA-total表达。为了避免量纲对计算结果的影响，首先将整个数据集进行标准化处理，使均值为0，方差为1。

利用ISIS(LASSO)、ISIS(LASSO)+JMI方法分别对此数据集进行变量筛选后，结合Yang等[20]提出的期望分位数回归方法，即在软件R中为KERE程序包,此期望分位数回归的数学定义为：

(7)

(8)

(9)

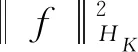
从具有不同降解率的44个基因中随机选择出2个基因Fgl2、Usp25,然后分别利用ISIS(LASSO)、ISIS(LASSO)+JMI方法对数据进行变量筛选，分别选择出12个基因。

首先以Fgl2基因为例，对ISIS(LASSO)+JMI方法筛选出来的前5个基因在进行标准化前的RNA-total以及Fgl2基因的RNA-4sU数据进行描述性统计，结果如表7所示。从表7发现，数据中最小值与最大值差值都很大，即表明数据波动范围大。

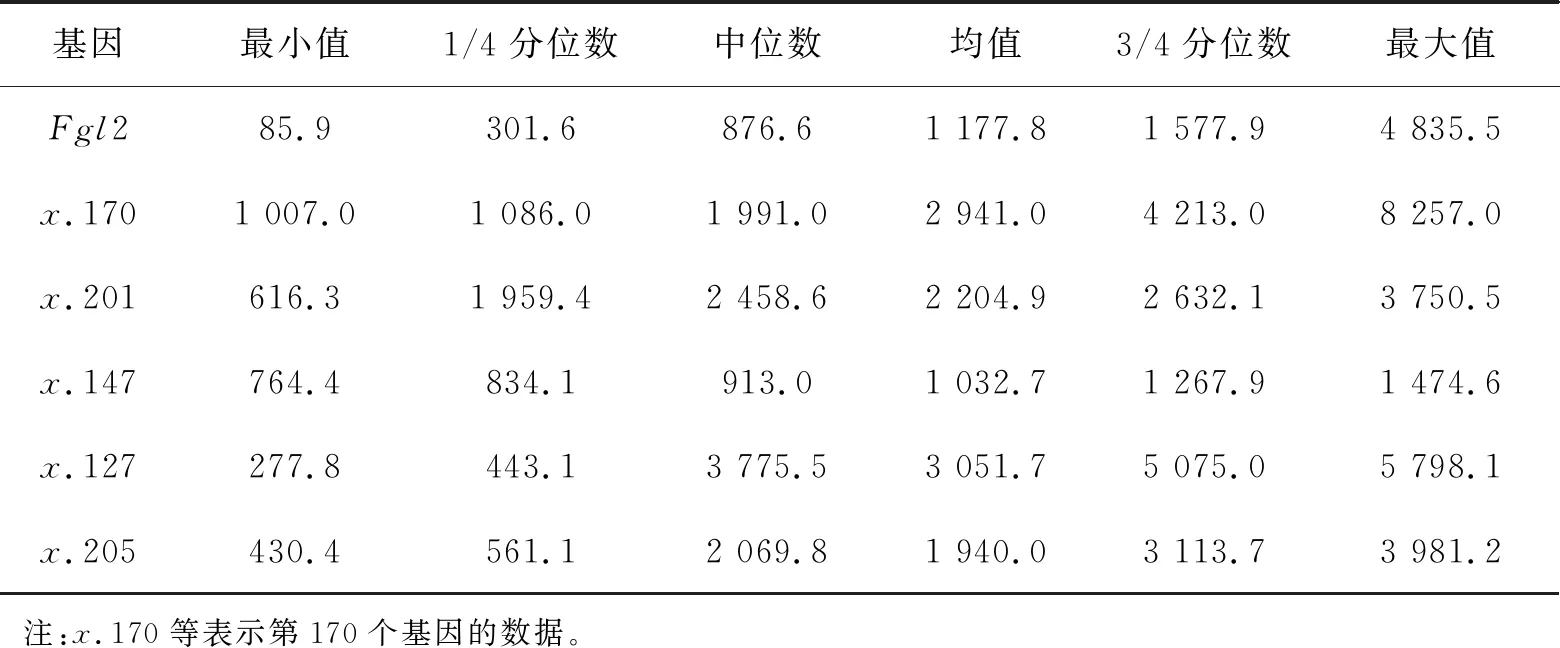
表7 Fgl2基因变量选择出的前5个基因的描述性统计

利用各基因下筛选出的12个基因的RNA-total表达作为上述2个基因的解释变量，仍以上述2个基因的RNA-4sU表达作为响应变量，在KERE算法下分别对2种方法筛选出来的数据集进行模型拟合，并计算出经拟合后的残差标准差，得到ISIS(LASSO)筛选下模型拟合结果(图2)和ISIS(LASSO)+JMI筛选下模型拟合结果(图3)，分别对应表8中的残差标准差结果。

图2 ISIS(LASSO)下的模型拟合

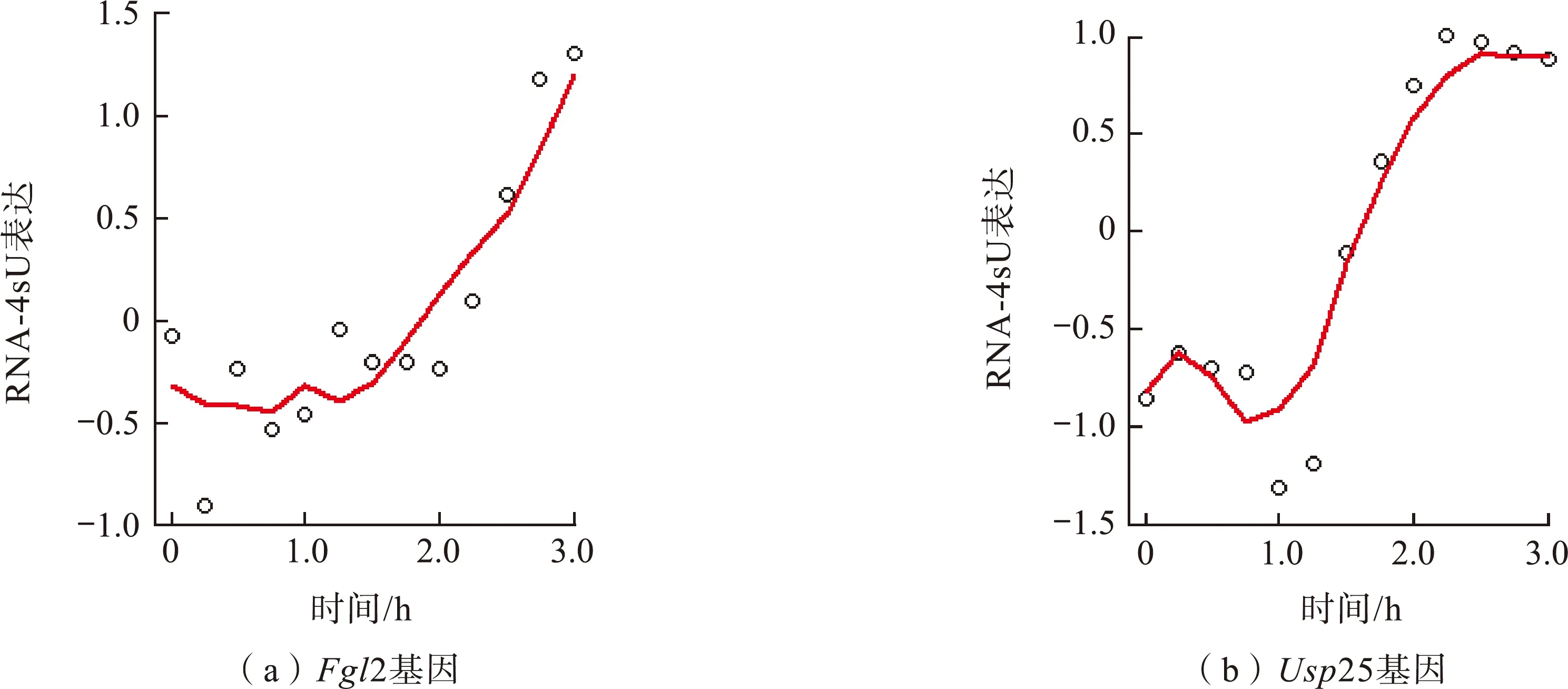
图3 ISIS(LASSO)+JMI下模型拟合

表8 拟合残差标准差

图2、图3中散点表示基因原有的RNA-4sU表达，曲线则表示在KERE算法下的拟合曲线。从图2和图3可以看出ISIS(LASSO)+JMI的筛选非线性变量的效果比原ISIS(LASSO)的效果好。从表8可知，与图1直观反映出的效果一致，表格中更客观地显示了拟合效果好的特点。所以利用ISIS(LASSO)+JMI选择出对预测响应变量有效的解释变量后，能在KERE法下进行较好效果的模型拟合。

4 结语

本文利用JMI与经典SIS的思想方法，研究将它们进行结合后，是否可对高维稀疏非线性回归模型中重要变量进行选择，并通过模拟试验以及相应的实例分析得到如下结论：第一，对于响应变量呈二分类变量类型的数据，采用本文所提出的ISIS(LASSO)+JMI(N)方法可以对经典的SIS方法进行改进，且效果较好；第二，对于解释变量与响应变量具有非线性关系的数据类型，采用本文提出的ISIS(LASSO)+JMI方法可以选择出非线性回归模型中的重要解释变量，解决了SIS不能处理非线性回归模型变量选择问题的弊端，对SIS有了很大的改进；第三，通过模拟试验二的结果分析，为提升不同复杂度下的高维稀疏非线性回归模型中变量选择的效果，本文所提方法还可以进一步研究。