广义Lp宽度积分的混合Brunn-Minkowski型不等式①

杨林，谭杨，罗淼

1.铜仁职业技术学院 信息工程学院，贵州 铜仁 554300；2.贵州师范大学 数学科学学院，贵阳 550025

若K为Rn(n>1)中的完备紧凸集，则称K为凸体． 支持函数是研究凸体的重要概念，其表达式为

h(K，u)=max{x·u：x∈K}u∈Sn-1

B，Sn-1分别表示Rn中的单位球和单位球面． 记

Minkowski线性组合为凸体之间的重要运算，其定义为：设K，L∈Kn，λ，μ为非负实数且不同时为0，K与L的Minkowski线性组合λ·K+μ·L∈Kn用支持函数可表示为

h(λ·K+μ·L，u)=λh(K，u)+μh(L，u)

Brunn-Minkowski理论中有诸多有意义的结果，详情请参阅文献[1-11]．

文献[1]研究的关于凸体K1，K2，…，Kn的混合宽度积分B(K1，…，Kn)表示为

其中

当K1=… =Kn-i=K，Kn-i+1=… =Kn=L时，B(K1，…，Kn)=Bi(K，L)． 若存在正实数λ，使得b(K，u)=λb(L，u)，则称K与L具有相似宽度．

设K1，…，Kn∈Kn，τ∈(-1，1)，文献[2]将文献[1]所定义的混合宽度积分推广为如下更一般的混合宽度积分B(τ)(K1，…，Kn)，表达式为

其中

b(τ)(K，u)=f1(τ)h(K，u)+f2(τ)h(K，-u)

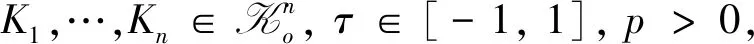
其中

(1)

等号成立当且仅当K与L具有相似广义Lp宽度；

(2)

等号成立当且仅当K与L具有相似广义Lp宽度．

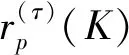
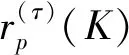
本文受文献[6-7]的启发，建立了如下不等式：

(3)

等号成立当且仅当K与L具有相似广义Lp宽度．

(4)

其中

等号成立当且仅当K与L具有相似广义Lp常宽度．

证由LpMinkowski加法知

引理2[12](Minkowski不等式)设f(x)与g(x)为可测集X上的非负可测函数． 若f(x)，g(x)∈L(p)，p>1，则

(5)

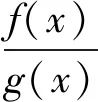
等号成立当且仅当f(x)=Mg(x)．

等号成立当且仅当f(x)=mg(x)．

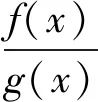
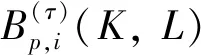
根据i

在定理1中取p=1时，有：

等号成立当且仅当K与L具有相似广义宽度．

在定理1中取Q=B时即为不等式(2)，在推论1中取Q=B时为文献[9]之结论．

由

可得

(6)

从而有

由i

在定理2中取Q=B时，得：

其中c同定理2中所定义，等号成立当且仅当K与L具有相似广义Lp常宽度．

在推论2中取p=1时，得：

等号成立当且仅当K与L具有相似广义常宽度．

现应用引理4给出不等式(1)的逆，即：

(7)

等号成立当且仅当K与L具有相似广义Lp常宽度．

证由

令

可得

(8)

根据公式(8)与不等式(6)，可得

由i

在定理3中取i=0，j=i，k=n时，有：

等号成立当且仅当K与L具有相似广义Lp常宽度．