箭图表示的绝对Clean性质①

孙情，杨刚

兰州交通大学 数理学院，兰州 730070

20世纪70年代，Gabriel、Auslander和Reiten建立了箭图表示理论． 经过近50年的发展，箭图表示理论不仅趋于完善，而且与群表示论、李代数和量子群、代数几何、数学物理等其他学科有深刻的联系．

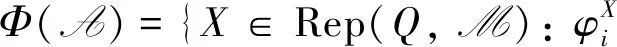
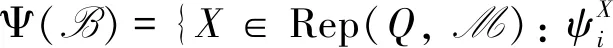
并研究了表示范畴中余挠对的遗传性． 文献[4]研究了箭图的表示范畴中的余挠对(Φ(A)，Φ(A)⊥)和(⊥Ψ(B)，Ψ(B))的完全性．

绝对Clean模类作为R-模范畴中一类特殊有限表现模类，关于Ext函子的右正交子范畴在同调代数的研究中有着重要应用． 文献[5]引入了绝对Clean的概念，从而引入了GorensteinAC投射模和GorensteinAC内射模的概念，并研究了Gorenstein同调理论是如何扩展到任意环R上的． 后来，文献[6]定义了绝对Clean复形，并且进一步研究了相关的Gorenstein同调理论．

1 准备知识

定义1令n≥0是整数． 如果存在正合列

其中每个Fi是有限生成的投射模(i=1，2，…，n)，则称模M是n有限表现模． 特别地，当n=1时，则称M为有限表现模． 如果存在正合列

使得每个Fi是有限生成的投射模(i=1，2，…)，则称M是超有限表现模．

定义2设C是范畴A中的对象类，且A中存在足够多的投射对象(内射对象)． 如果C包含所有投射(内射)对象，并且C关于扩张和满同态的核(单同态的余核)封闭，则称C是可解(余可解)的．

2 n有限表现表示与绝对Clean表示

定义3令i≥0是整数，M∈Rep(Q，M)． 如果存在正合列

其中Fi是Rep(Q，M)中有限生成的投射表示(i=1，2，…，n)，则称M是n有限表现表示． 特别地，当n=1时，称M是有限表现表示． 如果存在正合列

使得每个Fi是有限生成的投射表示(i=1，2，…)，则称M是超有限表现表示．

定理1设M∈Rep(Q，M)． 则M是n有限表现表示当且仅当每个Mi是n有限表现模(i=1，2，…，m)．

证必要性 因为M是n有限表现表示，所以存在正合列

其中Fj是有限生成的投射表示(j=1，2，…，n)，即存在行正合的交换图

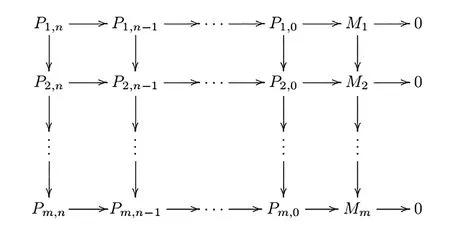
其中Pi，j是有限生成的投射模． 根据定义1知每个Mi是n有限表现模．

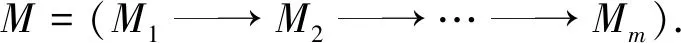
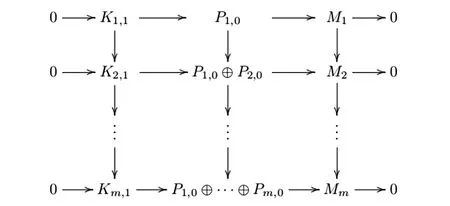
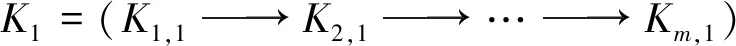
其中Fj是有限生成的投射表示(j=1，2，…，n)． 这便证得M是n有限表现表示．

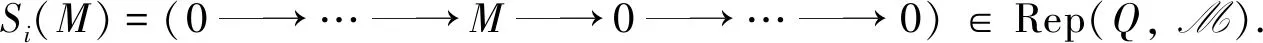
定理2设M∈Rep(Q，M)． 则M是超有限表现表示当且仅当每个Mi是超有限表现模(i=1，2，…，m)．

证类似于定理1可证．

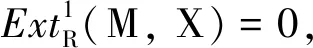
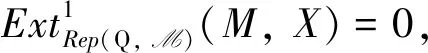
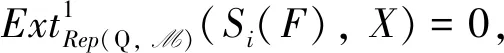
证必要性 显然成立．

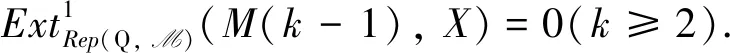
(1)

即有列正合的交换图

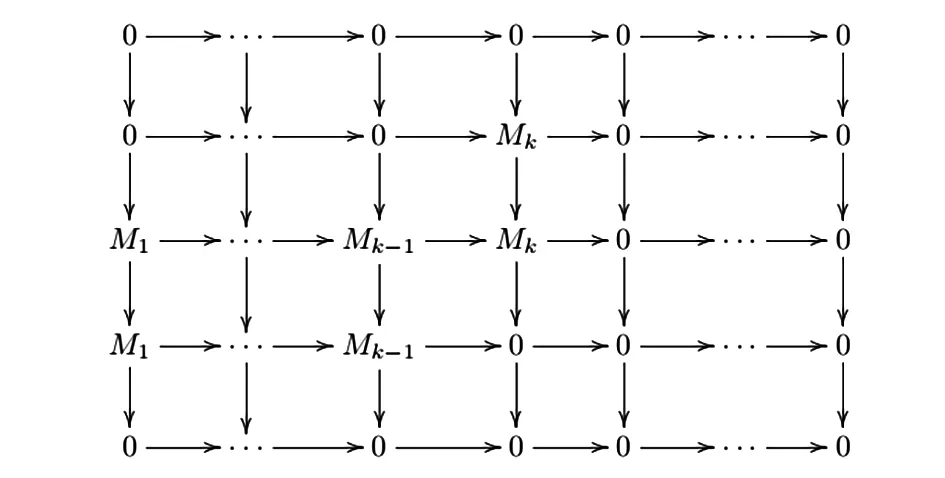
用HomRep(Q，M)(-，X)作用正合列(1)，可得长正合列

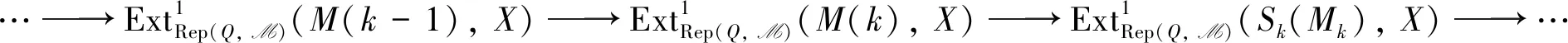
由归纳假设和条件可知

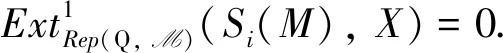
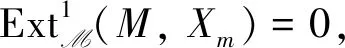
依次类推可得Kerdi，X1，X2，…，Xm都是绝对Clean模．

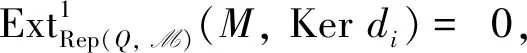
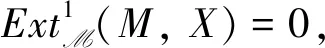
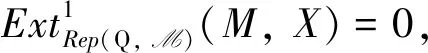
证类似于定理2可证．

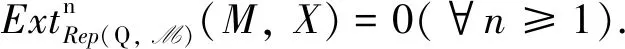
证充分性显然成立，下证必要性． 设M是超有限表现表示． 则存在正合列

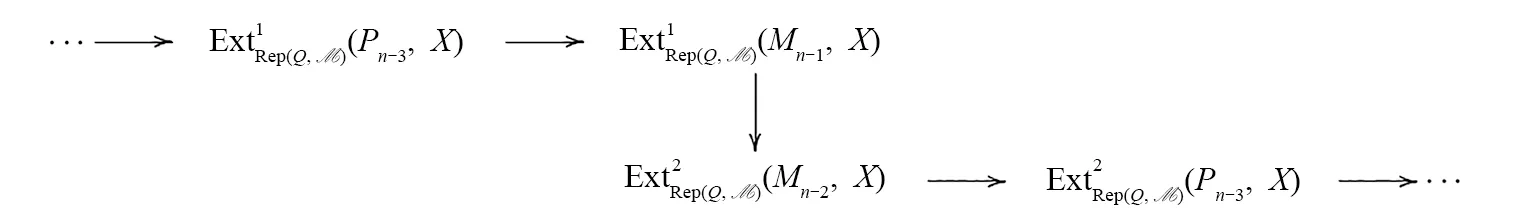
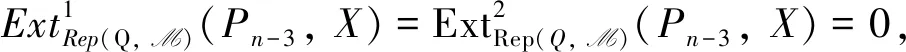
依次类推，利用维数转移可以得到

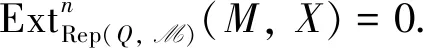
命题2绝对Clean表示构成的类是余可解类．

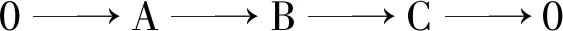
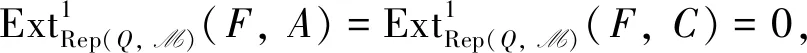
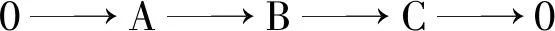
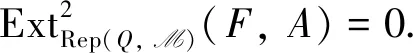
又因为任意内射表示是绝对Clean表示，所以绝对Clean表示构成的类是余可解类．