基于广义后缀树结合过滤因子的正则表达式匹配算法

林 婧 何震瀛

1(复旦大学软件学院 上海 201203) 2(复旦大学计算机科学技术学院 上海 201203) 3(复旦大学上海市数据科学重点实验室 上海 200433)

0 引 言

随着科学技术的飞速发展，数字化信息呈爆炸式增长，文本数据作为信息的载体，包含了大量宝贵的资源，而如何从这些数据中查询出有价值的信息，是人们日益关注的一个重要问题。

正则表达式具有强大而灵活的文本处理能力，是解决查询问题的一个重要手段，应用领域十分广泛[1-5]。

由于正则表达式与有限自动机完全等价[6],因此一般采用有限自动机来分析和匹配正则表达式。传统算法的匹配过程描述如下：对于给定的正则表达式Q，将其转换为自动机；一个待匹配的文本序列T，从T的起始位置开始运行自动机。每当自动机达到最终状态时，得到一个匹配结果[7-8]；然后继续从T的下一位置开始重新运行自动机，最终得到Q在T上匹配的所有字符串集合。这种算法需要从文本的每个位置开始逐一检验，当文本序列较长时，匹配效率低下。为此，研究者们提出了很多方法来加速正则表达式的匹配过程。MultiStringRE算法[9]首先计算出所有能够匹配正则表达式Q的文本的前缀集合。对文本序列T,得到包含这些前缀的起始位置集合，进而得到候选区间。利用类似Commentz-Water的算法来对候选区间中的子串进行验证，这样可以过滤掉某些位置，减少重复验证的次数。NRGrep算法[10]也是利用前缀因子来减少匹配次数。不同的是，它使用正则表达式的反向前缀(即正则表达式的后缀)，并使用反向自动机来对候选集合进行验证。GNU grep算法[11]提出了必要因子的概念。必要因子是匹配正则表达式的字符串中必须出现的子串。例如，正则表达式Q为(a|g)td*,则Q的必要因子集合为{t}。必要因子能够将正则表达式拆分为左右两部分，如Q中的必要因子t将Q拆分为(a|g)和d*。对这两部分分别构造两个自动机，在字符串中每个必要因子出现的位置，前后双向验证。

这些算法的主要问题如下：当一个文本序列含有多个前缀因子或必要因子时，会削弱减少匹配次数的能力；在匹配文本集合时，需要逐条记录进行匹配，运行时间与集合大小成线性关系，当文本集合较大时，匹配代价依旧非常昂贵。

因此，本文提出一种基于广义后缀树与过滤因子相结合的正则表达式匹配算法。将待匹配的文本序列集合构建成一颗广义后缀树，每条边包含一个字符，从根节点到某一叶子节点的路径即为一个后缀，叶子节点为包含该后缀的文本序列索引以及该后缀在文本序列中的起始位置。广义后缀树具有强大的剪枝能力，在其上运行自动机时，如果到达某一内部节点时就已经满足自动机的最终状态，将不会再遍历余下的分支，直接提取该内部节点下所有叶子节点所包含的信息。并且该过程相当于同时匹配含有该共享后缀的多个文本序列，这将节约大量的计算代价。然而当正则表达式中含有克林闭包时，自动机会在后缀树上进行很多不必要的匹配尝试，并不能起到很好的剪枝作用。通过在广义后缀树中定位前缀因子和必要因子，确定所有满足条件的文本序列候选区间，并根据前缀因子和必要因子的序列要求，产生更高效的过滤，从而提高整体匹配性能。通过实验可以证明该方法能够显著提高正则表达式在文本序列集合上的匹配性能。当正则表达式包含克林闭包时，将有更显著的性能提升。

1 正则表达式匹配定义

1.1 正则表达式

正则表达式是一种能够匹配一个或多个字符的模式字符串，由一系列普通字符和元字符组成。普通字符由美国信息交换标准码ASCII构成，元字符则包含了一些特殊的含义。正则表达式中的主要元字符如表1所示。

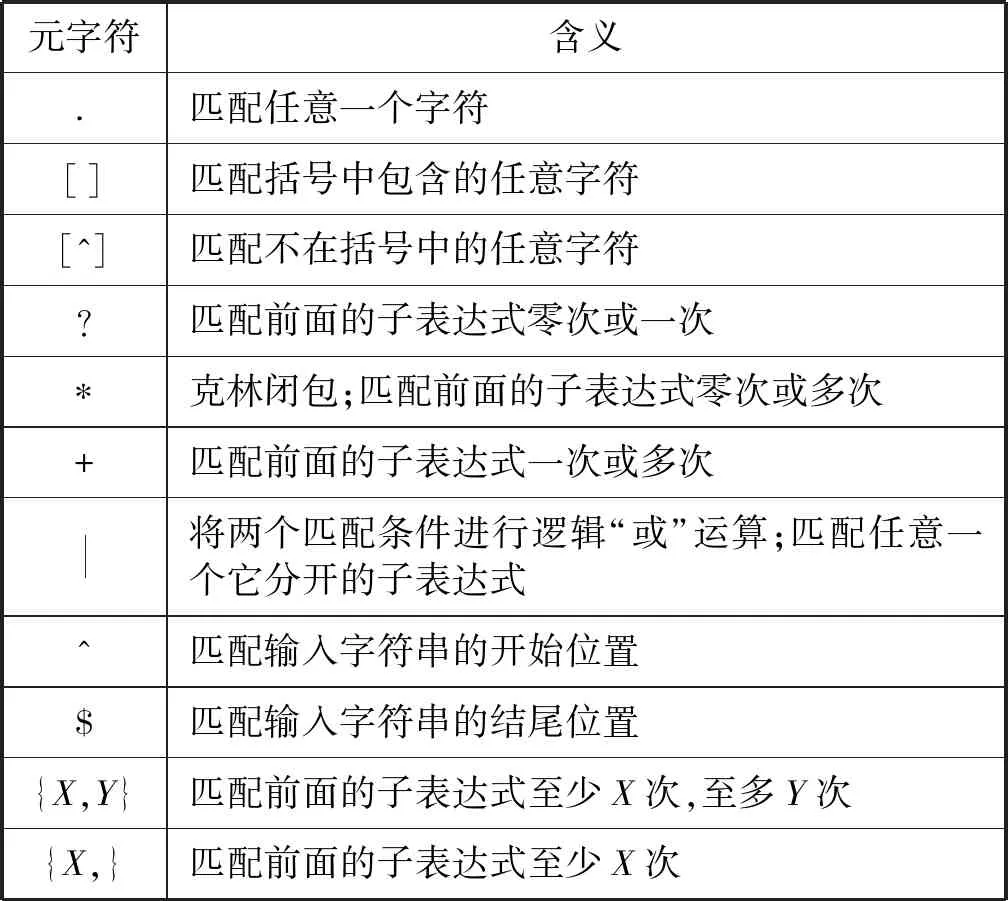
表1 正则表达式主要元字符

1.2 正则表达式匹配

本文中的字符串匹配，即给定一个正则表达式Q,一个文本T，得到T中能够满足Q所描述的所有字符串集合。如Q=t(a|c),T=ttatcdta,则Q在T上的匹配集合SQT={ta1,tc3,ta6}(下标为子串在T中的起始位置)。特别地，当正则表达式包含克林闭包时(尤其是包含“.*”时)，匹配文本T的字符串集合将包含很多子串，如Q=t.*，T=ttatcdta，则SQT={t0,tt0,tta0,ttat0,ttatc0,ttatcd0,ttatcdt0,ttatcdta0,t1,ta1,tat1,tatc1,tatcd1,tatcdt1,tatcdta1,t3,tc3,tcd3,tcdt3,tcdta3,t6,ta6}。

2 算 法

2.1 过滤因子

经典的正则表达式匹配算法将正则表达式编译为一个等价的自动机，对于文本中的每一个位置，都要重新运行一遍自动机来进行验证，最终得到所有的匹配结果。一些算法利用过滤验证技术，从正则表达式中提取出一个子串，在文本中快速定位子串，得到候选匹配区间。只有这些候选区间需要被自动机验证，加速了匹配过程。这些被提取的子串包括前缀因子和必要因子。

前缀因子是正则表达式中的前缀字符串，通常需要指定长度。如正则表达式Q=(a|g)td*,设定前缀因子的长度为2，则Q的前缀因子集合为Sp={at,gt}。匹配Q的任意一个字符串都必须以Q的前缀因子开始。对于文本T，前缀因子所在的位置就是候选匹配结果的开始位置，只需要从这些位置开始验证自动机。

必要因子是正则表达式的所有匹配结果中必须出现的最长子串。例如，正则表达式Q=(a|g)td*，则必要因子集合为Sf={t}。若正则表达式Q=(a|g)taad*，则必要因子集合为Sf={taa}。必要因子将正则表达式划分为左右两部分。例如，Q=(a|g)taad*，必要因子taa将其划分为两个子表达式(a|g)和d*。在文本中定位必要因子，然后以其为中心，左右分别运行拆分后的两个自动机，得到匹配结果。有些子串可能既是前缀因子，又是必要因子。本文为了高效利用前缀因子和必要因子，将包含在前缀因子中的必要因子剔除。

前缀因子和必要因子都是利用过滤技术，减少待匹配的候选区间，加速匹配过程。本文同时使用前缀因子和必要因子，增加过滤强度，进一步提高匹配效率。

2.2 广义后缀树

广义后缀树是对后缀树的扩展。后缀树是包含一个字符串s的所有后缀的Trie[12]结构，可以在O(|s′|)内确定另一个字符串s′是否为s的子串。而广义后缀树(Generalized Suffix Tree，GST)包含一组字符串的所有后缀，依旧可以将子串查找问题限制在O(|s′|)的时间复杂度内。如图1所示，广义后缀树的边包含一个字符，＄0是终端符号，叶节点为包含从自身到根节点的这条路径(后缀)的原始字符串s0的id以及该后缀在s0中的起始位置。为了更好地理解如何在GST上进行正则表达式匹配，本文首先介绍在GST上进行纯字符串匹配的算法。为了找到GST中包含子串s′的所有字符串，按深度优先搜索(DFS)顺序从根节点到叶节点的每个字符逐一与s′中的字符比较。如果s′的所有字符都出现在GST的某条路径p中，就可以从p的叶节点中得到相应的匹配结果。

图1 GST示例

2.3 基于GST的正则表达式匹配算法

GST具有很强的剪枝能力，若自动机在GST上运行到某一内部节点时就达到最终状态，将不必再遍历余下的分支，直接获取该节点下所有叶子节点的文本信息。并且该过程相当于同时匹配所有文本，有效提升了匹配速率。例如，给定文本集合T={tactgds,tadgt},正则表达式Q=ta。基于GST的正则表达式匹配算法步骤为：

1)根据文本集合构建GST。

2)将Q转换为自动机，在后缀树上以DFS的顺序运行。

(1)从根节点出发，匹配第一条边s，s≠t，匹配失败。

(2)继续尝试匹配下一条边c，c≠t，匹配失败。

(3)继续尝试匹配下一条边a，a≠t，匹配失败。

(4)继续尝试匹配下一条边t，t=t，匹配成功，遍历余下分支。

(5)匹配到t的子树分支a时，自动机达到最终状态，匹配完成。获取该节点下方所有叶子节点的信息，得到匹配Q的所有文本。本例中为文本0和文本1。从文本0的第一个位置开始匹配(索引为0)，从文本1的第一个位置开始匹配(索引为0)。

但当正则表达式中含有克林闭包时，自动机会在GST上进行很多无效的尝试，尤其是包含.*时，算法性能会受到严重影响。如Q=t.*m，自动机会在分支t的所有子孙进行匹配尝试，最终才发现没有匹配结果。又如Q=t.*，t下的分支节点全部可以匹配，但自动机依旧需要在所有分支上进行匹配尝试。当文本集合较为庞大时，GST的内部节点下可能会包含大量分支，逐一遍历时，算法的时间复杂度较高。

2.4 基于GST与过滤因子相结合的正则表达式匹配算法

为了解决GST面对克林闭包时效率低下的问题，同时进一步加速正则表达式在文本集合上的匹配过程，本文将GST与过滤因子相结合，提出一种高效的正则表达式匹配算法。

首先为正则表达式构建一棵解析树[13]，以提取过滤因子。解析树是一种存储正则表达式语法信息的二叉树。每个非叶子节点表示一个操作符，符号&表示连接左子树和右子树。解析树左子树的叶子节点集合就是前缀因子集合。从根节点到表示必要因子的叶子节点的路径上不能含有不确定性的元字符，如|和*。为了更好地划分前缀因子和必要因子，本文所运用的必要因子只从根节点的右子树开始选取。图2为正则表达式(a|c).*gt*d的解析树，它的前缀因子集合为{a,c}，必要因子集合为{g,d}。基于GST与过滤因子相结合的正则表达式匹配算法如算法1所示。

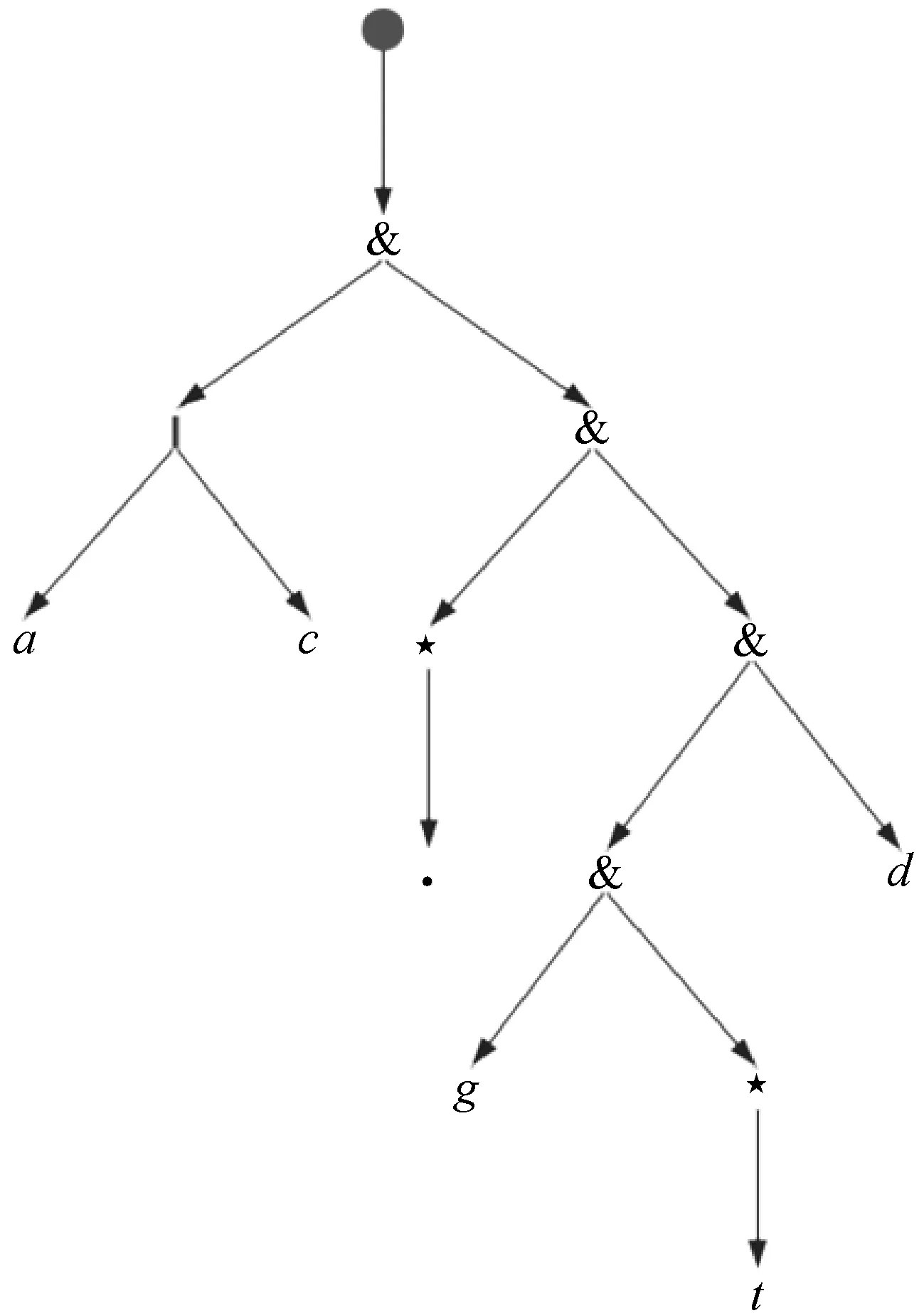
图2 Q=(a|c).*gt*d的解析树

算法1基于GST与过滤因子相结合的正则表达式匹配算法

输入：正则表达式Q,文本集合T。

输出：匹配结果集合R。

1.构造解析树，得到前缀因子集合P和必要因子集合F

2.根据P和F对Q拆分，得到子表达式集合regexCollect

3.对文本集合T构造GST

4.For eachpinPdo

//regex_match_on_GST(p,GST)的返回结果为

//((id1,index1),(id2,index2),…)

5.matchsp←regex_match_on_GST(p,GST)

6.For eachfinFdo

7.matchsf←regex_match_on_GST(f,GST)

8.For eachmp(idp,indexp)inmatchsp

//f0代表第一个必要因子,indexf0是f0在Tidp上的索引

9.R0=Verify(Tidp,indexp,indexf0,regexCollect(0))

10.Fori<-1 1 untilregexCollect.size

11.Ri=Verify(Tidfi,indexfi-1,indexfi,regexCollect(i))

12.ReturnR

得到正则表达式的过滤因子后，将其与GST相结合，加速正则表达式在文本集合上的匹配过程。如给定文本集合T={tactgds,tadgt},Q=(a|c).*gt*d。则前缀因子集合为{a,c},必要因子集合为{g,d}。利用过滤因子将Q拆分为子表达式集合regexCollect={(a|c).*,gt*,d}。对文本集合T构造GST，如图1所示。在GST上匹配前缀因子，前缀因子a的匹配结果为{(0,1),(1,1)},((0,1)表示文本T0的第一个位置)，前缀因子c的匹配结果为((0,2))。在GST上匹配后缀因子,匹配g的结果为{(0,4)，(1,3)},匹配d的结果为{(0,5),(1,2)}。将前缀因子的匹配结果与第一个必要因子的匹配结果相结合，得到第一个子表达式的验证区间。之后对于剩余的每个必要因子，根据它与前一个必要因子的文本位置信息，依次得到后续的子表达式的验证区间。对于最后一个子表达式，验证区间为最后一个必要因子在文本中的匹配位置到文本末尾。将各个子表达式的匹配结果合并，得到最终匹配结果。算法1描述了基于GST与过滤因子相结合的整体算法流程。

3 实验与结果分析

为了测试基于GST与过滤因子相结合的正则表达式匹配算法的有效性，本文在两个真实的数据集上进行实验，分别是来自NCBI的BLAST蛋白质序列数据集(https://blast.ncbi.nlm.nih.gov/Blast.cgi)以及DBLP-Citation的论文记录数据集(http://arnetminer.org/DBLP Citation)，每个数据集分别抽取10 000条记录。本文采用两种类型的正则表达式来评估算法在数据集上的性能，分别是人工合成的正则表达式和谷歌RE2工具(https://github.com/google/re2)自动生成的正则表达式。每个数据集分别包含10个正则表达式，5个由人工合成，5个由RE2自动生成。每个正则表达式查询在相应的数据集上运行10次，取平均性能。

经典的正则表达式匹配算法，将正则表达式转换为自动机，在文本的每个位置运行一遍自动机，得到全部匹配结果。其他算法如GNU Grep等，当一个序列中存在多个匹配结果时，只获取匹配的第一个结果。而本文算法是能够匹配序列中的所有结果，因此无法公平地进行比较。本文比较的三个算法为经典的正则表达式匹配算法、基于广义后缀树的正则表达式匹配算法、基于广义后缀树与过滤因子相结合的正则表达式匹配算法。

实验所有的算法都是用Scala实现的，并使用C++来提取前缀因子和必要因子。实验是在Intel Core i5-7400 3.00 GHz CPU上进行的，操作系统是Windows 10。该程序在JVM中执行，其参数为java-Xmx4096m。

对于每个数据集，随机抽取5个正则表达式展示实验效果。抽取的正则表达式如表2所示。

表2 抽取的部分正则表达式

实验结果如图3-图4所示。

图3 蛋白质数据集实验结果

图4 论文数据集实验结果

由实验结果分析可见，在两个数据集中，GST+Filter的匹配效率均优于其余两种算法。在蛋白质数据集中，其最大时间开销为3 s，平均时间开销为0.613 s；在论文数据集中，最大时间开销和平均时间开销分别为8.9 s和2.8 s。而GST算法在两个数据集上的平均时间开销为84.4 s和60.2 s，经典算法在两个数据集中的平均时间开销为93.8 s和76.8 s。GST算法的匹配性能取决于具体的数据集和给定的正则表达式，在不包含克林闭包的情况下，GST算法具有优异的匹配性能。但当包含克林闭包时，GST算法的性能可能会受到影响。如对于蛋白质数据集上的Q3e查询及论文数据集上的Q5p查询，GST算法的时间开销已经近似于经典算法，时间复杂度较大，因此影响到GST的平均匹配性能。这主要取决于广义后缀树的结构以及给定的正则表达式。平均而言，GST+Filter算法的时间开销与经典匹配算法相差两个数量级。并且无论是否包含克林闭包，GST+Filter算法始终具有优异的匹配性能。

4 结 语

正则表达式具有强大的表达能力，能够提供复杂的查询逻辑，在很多领域内都发挥着重要作用。本文研究了正则表达式的匹配问题，提出一种基于广义后缀树与过滤因子相结合的正则表达式匹配算法。本文首先介绍了过滤因子与广义后缀树的概念，将文本集合构建成广义后缀树，利用过滤因子将正则表达式进行拆分，在广义后缀树上匹配过滤因子，根据过滤因子的序列位置信息来确定验证空间。本文算法具有强大的过滤能力，并且能够同时匹配多条文本，进一步提高了正则表达式在文本集合中的匹配效率。实验结果表明基于广义后缀树与过滤因子相结合的匹配算法能够有效提升正则表达式的匹配性能，特别当正则表达式中包含克林闭包时，性能提升尤为显著。