基于高斯模糊的CNN的单幅图像超分辨率重建算法

张华成 纪 飞 钟晓雄 陆 瑛

1(桂林电子科技大学计算机与信息安全学院 广西 桂林 541000) 2(广西中烟工业有限责任公司信息中心 广西 南宁 530001)

0 引 言

单幅图像超分辨率重建(Single Image Super Resolution Reconstruction，SISR)的目标是将输入的低分辨率图像(LR)重建为高分辨率图像(HR)，以修复由于硬件限制或者不良的外界环境在图像采集时造成的图像显示不清晰、图像质量低等问题[1]。由于SISR能够复原图像的部分高频细节，这项技术便被广泛应用于从安全和监视成像到医学成像等需要按需提供更多图像细节的领域。

目前为止SISR的研究者们已经提出了许多方法用于提升图像重建的效果，依据这些方法的性质，可以将它们分为三类：基于插值的方法[2]、基于重建的方法[3]和基于学习的方法[4-8]。基于插值的方法主要是利用现有的图像像素点的周边信息，在中心点的四周插入像素值进行重建。尽管基于插值的方法计算速度快，然而该类方法通常提供过于平滑的重建图像，留下了振铃效应，视觉效果较差。基于重建的方法如迭代反投影法、凸集投影法、最大后验概率估计法等，都是基于信号处理理论实现成像原理的逆过程，将在成像过程中丢失的高频信息复原。这类方法可以恢复出相对清晰的图像，但是通常也会忽略少许细节方面的内容。由于深度学习的不断发展促使基于学习的方法逐渐成为SISR重建研究任务中的主要方法，这类方法主要通过神经网络去学习LR图片和HR图片之间的映射模型，而后利用习得的模型完成图像的超分辨率重建。其中Dong等[9]首次把深度学习的方法使用于单幅图片超分辨率重建(SRCNN)任务上，后来他们又在SRCNN的基础上做出改进，即并没有把原始LR图像进行插值放大后才作为输入放进网络，而是直接把LR图像放入网络中，然后在整个网络结构的最后一层使用反卷积层实现比例的扩大，减少了网络的参数，提升了网络的运算速度(FSRCNN)[10]。Kim等[11]将残差网络(ResNet)[12]的思想引入SISR的工作中来，并在训练过程中，使用不同比例大小的图片同时训练，旨在建立一个多尺度的超分辨重建模型，但是该方式重建的HR图片视觉效果并不是很好，细节恢复较差(VDSR)。Kim等随后将循环神经网络(RNN)用于超分辨问题中，同时利用残差的思想提升了性能，但是与VDSR两者的效果非常接近(DRCN)[13]。但是，值得注意的是，上述基于学习的SISR重建方法，在学习映射模型过程中所使用的输入样本，都是HR图像通过Bicubic方法下采样得到，但是实际应用中，会包含多种退化因素，比如图片模糊不清、因环境或硬件导致的噪声等，这些都会对习得的网络模型的泛化能力有不同程度的影响，使得模型在测试集甚至真实场景的使用中表现得不如人意。

针对上面提到的问题，本文设计一种更加有效的图像超分辨率重建方法：通过在Bicubic下采样退化得到的LR图像输入网络模型前加入高斯模糊核，以增强下采样图片与真实低分辨率图片的相似度，进而提高模型的重建效果，并在网络中使用全局残差结构，只学习HR图片和LR图片的差值信息，提升网络性能，在网络末端使用亚像素卷积层(pixel shuffle)[14]进行上采样，实现HR图像重建。最终的实验结果显示，与类似的方法相比，本文方法有着更快的网络收敛速度、更好的重建效果。

1 本文算法

SRCNN建立了三层神经网络模型，本文提出的SISR方法是在SRCNN的基础上，以其三层结构的网络模型为原型，利用全局残差的思想进行训练。这个三层结构可以用如下三个阶段描述：

(1)特征提取阶段。在低分辨率图片(LR)输入网络前，与一个高斯模糊核进行卷积操作，获得LR图片对应的高斯模糊退化图(GLR)，然后将GLR图片通过复制填充法放大至与输入的LR图片同样尺寸，作为伪噪声源；其次将LR图片与一个通道数为64的3×3的小卷积核卷积，从而得到一个通道为64的特征图，完成特征提取。

(2)非线性映射阶段。将特征提取阶段获得的特征图与多个同样大小的卷积核串联卷积，完成非线性映射，进而提高网络的拟合能力，此处我们将通过非线性映射的特征图称为FLR。

(3)重建阶段。将LR图片、GLR图片、FLR进行维度统一化处理，以全局残差的方式完成信息融合，再利用亚像素卷积进行最后的图像放大操作，从而得到最终的重建HR图像。

本文算法的网络结构如图1所示。

1.1 高斯模糊退化

为了改善超分辨率重建任务的仅采用插值法降采样得到LR图片的问题，提高模型的泛化能力，本文引入了高斯模糊核，高斯模糊[15]也叫高斯平滑，它将图片按中心划分，让每个像素点对应的权重值随着它们到中心点距离的不同而改变，这个特点是利用正态分布实现的。该分布的一维形式是：

(1)

式中：∂代表θ的均值；φ是θ的方差。因为计算平均值的时候，中心点即是原点，所以∂等于0。根据其一维函数，推导得到的二维函数为：

(2)

式中：G(θ,y)即为本文所使用的模糊核。

本文通过将高斯模糊核与插值法降采样得到的LR图片卷积，提取模糊信息，来增强训练使用的LR图片特征，提高泛化能力，该过程如式(3)所示。

L=(H↓s)⊗G(θ,y)

(3)

式中：⊗表示原始的高分辨率图片H降采样后与高斯模糊核G(θ,y)的卷积操作；↓s表示缩放比例为s的下采样操作；L为通过高斯模糊核提取的模糊特征图。

1.2 非线性映射

由于在图像处理任务中，特征提取的等级随着网络深度的加深而变高，且网络结构的深度越深该网络获取的特征就越多。因此在非线性映射阶段，本文采用了18个3×3×64的卷积核串联的深度特征提取结构，通过加深网络深度来提高网络特征提取能力；每层网络通过使用修正线性单元函数ReLU来加快网络收敛。

1.3 残差网络

一般情况下，一个网络模型的深度与重建的效果成正比，不过伴随着深度的加大，如梯度消失、梯度爆炸等训练过程中常见的问题也就显现出来，而残差网络则很好地处理了这些问题。残差网络最重要的组成是残差学习单元，在一个多层神经网络中，假设它的输入是X时，其输出记为H(X)，各个网络层之间主要学习到的是F(X)=H(X)-X，即输入与输出之间的差值，在网络进行训练的过程中，输入值保持不变，作为恒等映射直接与网络层学习值相加，这样网络学习特征所需要的参数大量缩少的同时也保证了深层网络的有效性。一个残差单元可以用式(4)表示。

Y=(x,{Wi})+Wsx

(4)

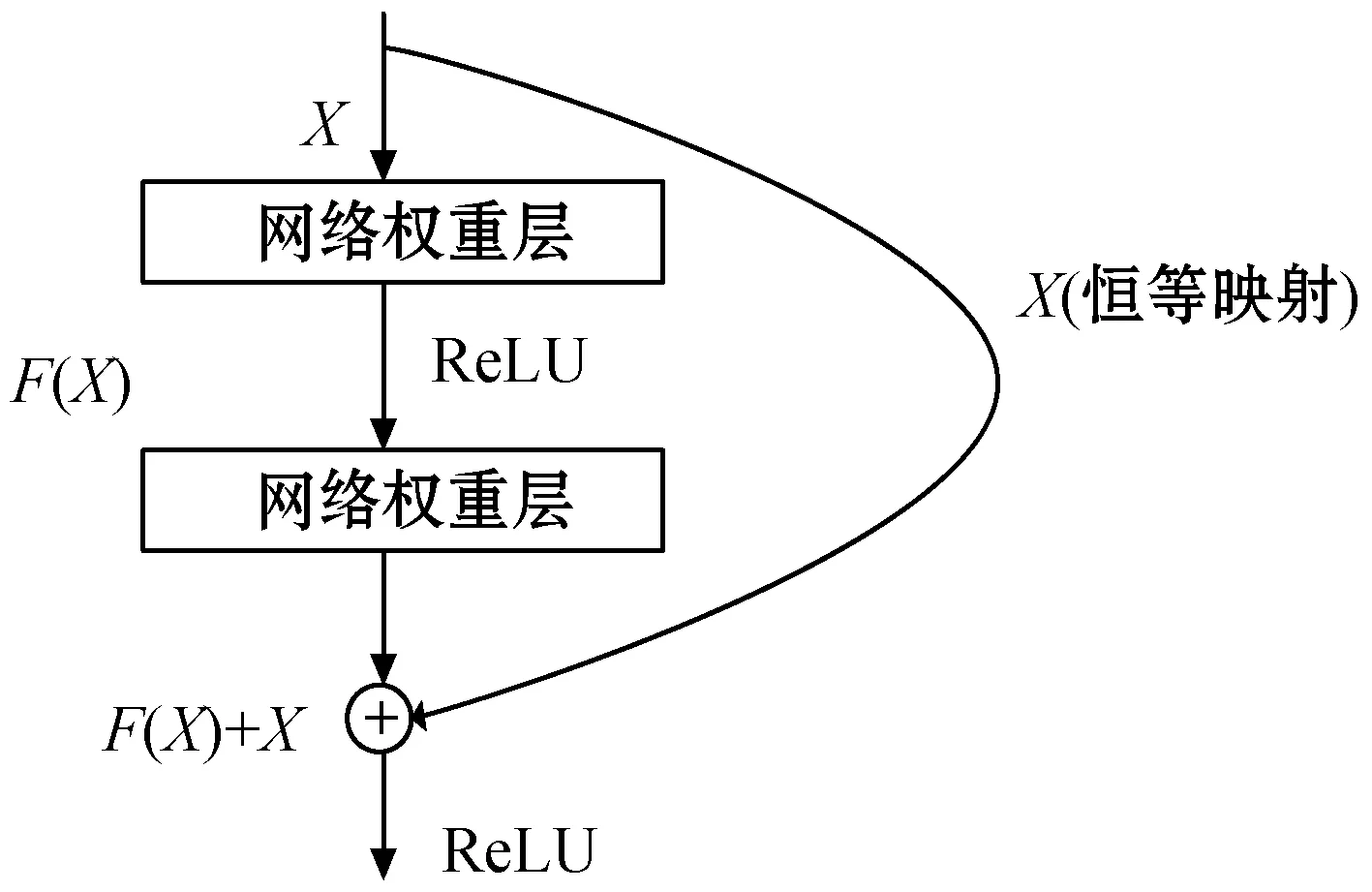
图2 残差单元结构

1.4 亚像素卷积

为了减少网络的参数，提升训练速度，在网络末端才对图像进行放大，因此通过卷积神经网络学习获取的特征图只是原始输入LR图像的比例大小。然而常用的特征图放大算法如插值法、反卷积法通常会带入过多的人工因素，而使用亚像素卷积层会大大降低这个风险。亚像素卷积层的做法是：假设对原图放大s倍，那么就生成s2个相同尺寸的特征图，然后将特征图每个像素的s2个通道重新排列成一个s×s的区域，对应HR图像中的一个s×s大小的子块。假如原始图像高为H、宽为W，那么网络末端生成的特征图大小可以表示成H×W×s2，通过亚像素卷积层后可表示为则sH×sW×1，即我们需要的高分辨率图片的比例大小。

1.5 损失函数

本文选用L1范数[16]损失函数作为整个网络模型的目标函数，该损失函数把目标值Yi和估计值f(xi)的绝对差值的综合S最小化。其表达式如下：

(5)

L1范数相对于其他损失函数能够让重建结果得到一个更高的峰值信噪比(PSNR)，而一般情况下经SISR后得到的图像的PSNR越高，说明模型的效果也就越好。

2 实 验

本文实验使用的系统是Ubuntu16.04，整个实验所使用的是在系统上搭建的Pytorch框架，在PyCharm上进行实验测试。电脑的硬件配置为Intel®CoreTMi7-8700 CPU @ 3.20 GHz×12，NVIDIA TITAN Xp/PCIe/SSE2。使用DIV2K[17](包含800幅2K分辨率的图片)数据集作为训练集，为了提升训练效果，对DIV2K数据进行数据增强：将图片块进行水平、垂直方向的翻转以及90°、180°、270°的旋转。

本文分别在放大倍数为2、3、4的时候与Bicubic、SRCNN、文献[18]、DRSR[19]、VDSR算法在不同测试集下进行比较。使用Set5、Set14、BSD100三个基准测试集对算法的效果进行验证。训练过程中在原始图像输入网络前裁剪为64×64的子像素块，并将它与相对应的HR图像的像素块组成训练数据。本文算法实验的学习率设置为1e-4，每经过2×105的小批次更新便将学习率减半；在训练数据迭代时，使用Adam对网络中各个层的权重进行更新。

2.1 损失函数选择

在相同的网络参数设定以及同样的训练批次下(均为200次)，相比于常用的损失函数均方误差(MSE)，以放大比例为2倍的重建任务中，在Set5测试集下，L1范数损失函数和MSE损失函数的PSNR值如图3所示。

图3 L1范数损失和MSE损失效果

可见，L1范数损失比MSE损失有着更高的起点、更快的收敛速度，以及更高的PSNR值。

2.2 高斯模糊核尺寸选择

一般情况下卷积核的尺寸越大，则其感受野就越大，获得的图片信息就越多，特征获取得也就越好。但是大的卷积核会导致计算量增加、性能降低。而考虑到高斯模糊核的选择是固定的，即不随网络的反向传播而更新权重，因此在高斯模糊核的尺寸上，可能不遵循一般卷积核尺寸的选择规律，所以本文在以损失函数为L1范数损失、放大比例为2倍、测试集为Set5的前提下分别对比了不同尺寸的高斯模糊核对实验结果的影响，如表1所示。

表1 不同尺寸高斯模糊核在Set5测试集下的PSNR平均值

可以发现，在尺寸为5×5的高斯模糊核下，可以获得更高的PSNR。

2.3 客观评价

与其他方法类似，本文采用PSNR(峰值信噪比)作为重建的HR图像质量的客观评价指标。原始HR图片Y和经算法重建得到的图片Y′相对应的PSNR(dB)计算公式如下：

(6)

(7)

式中：I表示一个大小是m×n的原始的HR图片；K表示通过网络模型后得到的图片；m、n分别代表图片的宽和高。由于网络深度的加深以及增加了多方信息融合，本文算法的PSNR平均值与传统的Bicubic算法相比有明显的提高，相比于其他基于CNN的算法也均有提高，实现了更好的重建效果。本文算法在放大倍数为2的时候，比其他对比算法有更大的差值，使用Set5作为测试集时，重建图片的PSNR平均值达到了37.65 dB，相比于最原始方法提高了3.99 dB。不同算法在不同测试集中以2倍、3倍、4倍的比例放大时的PSNR值分别如表2-表4所示。

表2 不同算法在测试集Set5的PSNR平均值 单位：dB

表3 不同算法在测试集Set14的PSNR平均值 单位：dB

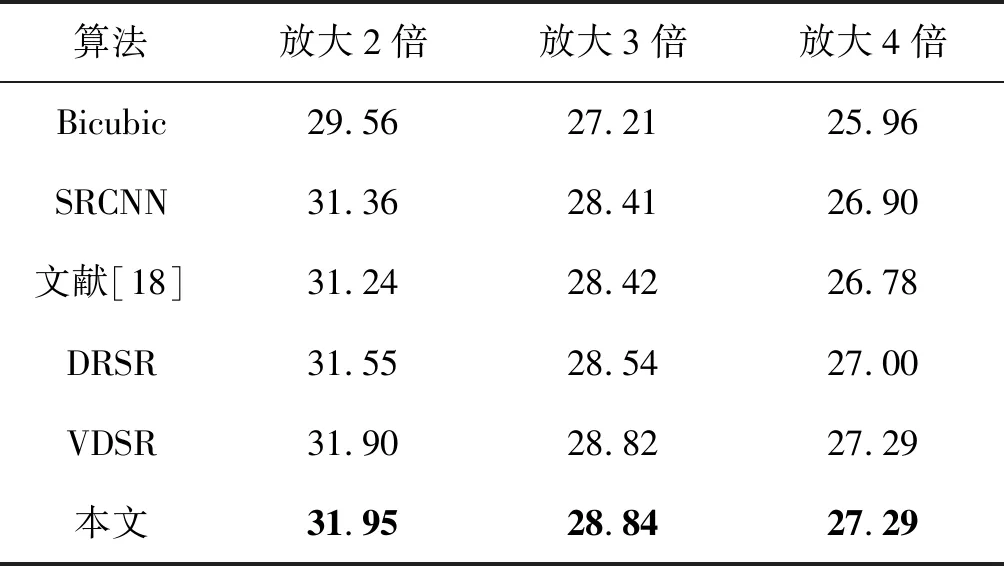
表4 不同算法在测试集BSD100的PSNR平均值 单位：dB

2.4 主观效果

图4、图5展示了本文方法与其他几种方法在测试集Set5中的部分图像以2倍放大比例下的重建效果。通过对图4、图5的观察可以发现：本文方法在进行SISR时，相比其他几种方法有更好的重建结果和更清晰的细节表现。

(a)原始HR图片 (b)文献[18]

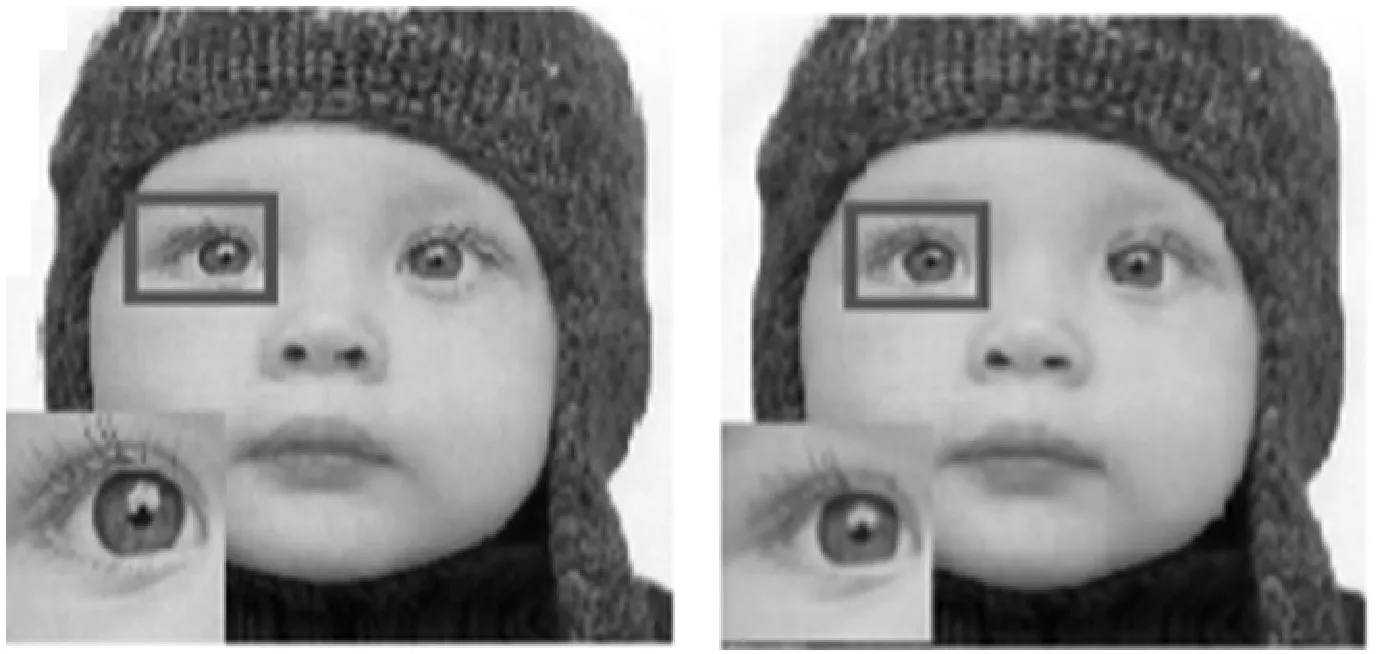
(a)原始HR图片 (b)文献[18]

3 结 语

本文针对图像超分辨率重建过程中退化模型单一的问题(主要通过Bicubic对HR图像进行下采样)，提出了基于高斯噪声的CNN的单幅图像超分辨率重建方法，通过Bicubic下采样与高斯模糊核结合，初始化网络输入图片，并使用残差网络学习LR图像和HR图像之间的残差信息，然后将模型习得的残差信息、Bicubic插值降采样信息、高斯模糊后的信息融合，最后使用亚像素卷积层，即不需要将输入的LR图像经插值扩充至与目标HR图像同样的像素大小，从而降低了模型的计算量。实验表明，相比于Bicubic、SRCNN、文献[18]、DRSR、VDSR等方法，在不同放大倍数下，本文方法均实现了较好的重建效果。但本文只在加深网络深度的同时，通过高斯模糊结合Bicubic降采样的方式实行全局残差信息融合，未来将在如噪声、翘曲等退化方式和低频信息、高频信息的融合方式上继续研究，进一步提高超分辨率的重建效果。