基于多目标进化算法的自驾游用户导航规划*
2022-01-27胡湘兰徐运保王求真
胡湘兰, 徐运保, 王求真
(1.湖南工程学院 管理学院,湖南 湘潭 411005;2.湘潭大学 计算机学院·网络空间安全学院 ,湖南 湘潭 411105)
0 引言
目前越来越多的用户在旅游时会选择自驾游模式,然而道路建设的日新月异使得交通网络变得越来越错综复杂,用户也不得不选择导航软件进行导航.导航软件推荐的线路越来越多,让用户对自驾出行路线的选择产生了困扰.用户可能会选择路程最短的那一条,也可能会选择耗时最少的那一条,因为短的路程可以减少车辆的油耗,而少的耗时可以节约出行的时间.综合考虑,如何从这众多的路径中选择一些路径使得这些路径既是路程最短的也是耗时最少的是本文研究的主要问题.
对导航目标进行量化的多目标导航问题本质上可归结为多目标最短路径问题.目前主流的解决方法有两种,一种是通过循环搜索第k短路径,构造新集合做交集来产生备选路径[1];另一种就是使用遗传算法模拟生物进化来得到优秀解[2].
模拟生物进化的遗传算法是目前求解多目标最优解的最常用算法,精英遗传保留的多目标优化算法在其迭代过程中保留了良好的解,以下是一些流行的精英主义多目标优化算法.Deb等[3]提出了计算复杂度较低的精英多目标遗传算法NSGA-II,在它的迭代过程中,它保留了两种类型的解:非支配解和人群中最不同的解,通过这样做,算法保持了其解决方案的质量和多样性,实验结果表明,该算法在求解多目标优化问题的各种最优解集方面是非常成功的.谢承旺等[4]提出了一种带差分局部搜索的改进型NSGA2算法.新算法利用差分进化中变异算子的定向引导作用,抽取其中的差分向量,并与NSGA2算法结合以改善解群的分布性.李密青等[5]提出了一种用最小生成树的边的权值来表示个体聚集距离的方法,并且对NSGA-2的交叉算子和变异率进行了改进.实验结果表明,与NSGA-2相比,该方法(MST-NSGA-2)在解的分布度上有较大的提高,并且有着良好的收敛性.Li等[6]为了在减少计算量的同时保持局部搜索策略的优势,针对NSGA2(NSGA2- dls)算法提出了一种基于密度的局部搜索方法.Qing等[7]提出了一种利用最小生成树边缘权值来度量个体拥挤距离的新方法,改进了NSGA-2的交叉算子和突变率.王慧莹[8]提出精英替换策略来加速种群的优胜劣汰,种群每进化一代,选取上一代种群中若干个最优解替换当前种群中表现最差的若干个解;分析并指出自适应遗传算法在调整遗传参数上存在的不足,针对其不足对遗传参数的调整策略进行改进.马硕[9]基于非支配排序遗传算法对车辆路径规划提出改进方法.郑金华[10]论述了MOEA 的性能评价方法,阐述了构造Pareto 最优解集的方法,刻画了保持进化群体分布性的方法和策略,详述了MOEA 的测试方法.Jensen[11]提出了一种新的、高效的非支配排序算法,大大提高了多目标进化算法的处理速度.
针对目前主流多目标分配算法,其优点是优化目标个数任选,非劣最优解分布均匀,并允许存在多个不同的等价解;但仍存在以下3点问题:
a)算法计算复杂度较高(O(mN3),m为目标函数个数,N为种群大小),当种群较大时,计算相当耗时.
b)缺乏精英策略,精英策略可以加速算法的执行速度,而且也能在一定程度上确保找到的满意解不被丢失.
c)对共享参数σshare的依赖性较大.
本文采用了时间复杂度较低且准确率较高的基于NSGA-II多目标进化算法,针对以上3点缺陷,进行了改进:
a)提出了快速非支配排序法,降低了算法的计算复杂度(O(mN2),m为目标函数个数,N为种群大小).
b)引进了精英策略,扩大采样空间,使得最佳个体不会丢失,迅速提高种群水平.
c)提出拥挤度和拥挤度比较算子,不再需要指定共享参数σshare,保持了种群的多样性.
本文所运用算法,不仅保证了所求的时间、路径双目标下最优解的总时间、总路程较短,而且充分考虑了遗传子代的均匀分布性和多样性,使得最终求得的最优解有较高的准确性.
1 问题模型
在城市交通网络图上选择两个城市,其中一个为出发城市,另一个为到达城市,找出那些可使多个目标同时达到最优的路径,如路程最短,经过城市的数目最多,交通信号灯数目最少等.本课题选取的目标为路程最短和耗时最少,其中路程仅与路径总长度有关,而耗时受路径总长度,交通信号灯数目,道路的类型等多个因素影响,需全面考虑.
将实际问题转化为图论模型,城市交通网络图用平面图表示,如图1所示,城市网络交通图中的各个地点表示为平面图中的各个顶点,那么起始城市和到达城市分别定义为起点和终点,地点之间的道路表示为顶点之间的边,道路的长度和耗时经过量化后表示为边的两个权.

图1 城市交通网络平面图Fig.1 Plan of urban transportation network
如图1所示,设图中共有n个顶点,编号为0,1,2,…,n-1,起点为u,终点为v,点u到v的距离为Suv,点u到v需要的时间为Tuv,设ai∈[0,n-1],问题要求找出一条路线:a0,a1,a2,…,ak-1,其中k∈[1,n],a0=u,ak-1=v,优化函数如公式(1)所示:
(1)
2 基于NSGA-Ⅱ算法多目标路径优化
2.1 编码与初始种群的生成
采用直接编码的方式,一条起点到终点的路径即为一条染色体,染色体上的每一位基因代表路径上的点,一个个体只包含一条染色体,种群中的最优个体代表着问题的最优解.
在进化的初始阶段,需生成一个初始种群,为了保证初始种群中的每个个体所代表的解都是合法的,初始化的路径需要满足一些条件.首先,路径的起点和终点必须是由用户指定的导航的起点和终点,由于本课题需要最小化路径的总路程和总时间,那么路径上的点不能重复,需要记录路径经过了哪些点来保证点不重的性质.
初始路径生成的具体步骤如下:
①设当前路径上的最后一个点为end,初始now为图的起点;
②确定now能到达且能到达的点不在当前路径上的点的个数num;
③生成一个随机数rand∈[0,num-1],选取随机点,更新now;
④重复②③随机选点的步骤,直到某一个点与终点直接相连.
在生成路径的途中,如果某个点不存在后继点,则结束本次路径生成从起点重新开始.
2.2 目标值的计算
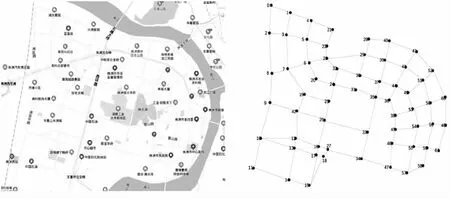
设种群的总个体集合为S,其中每段路径Xi的两个目标分量为总路程F(Xi)、总时间G(Xi),i=1,…,n,对于任意的两段路径Xn和Xm,当满足F(Xn)≤F(Xm)且G(Xn) 图2 Xn与Xm的Pareto支配关系图Fig.2 Pareto dominance diagram of Xn and Xm 在初始种群中,求得的非支配解的集合S′={X1,X2,X3,…,Xi}的Pareto等级定义为1,将这些非支配解组成的集合从初始种群中删除,即S″=S-S′,在群体S″中求出此时的非支配解,并定义其Pareto等级为2,按照此规则,依此类推,直至得到初始群体中所有个体的Pareto等级.分别以两个目标分量F和G作为二维坐标的横坐标和纵坐标,可以得到各个个体的Pareto等级坐标分布图,如图3所示,圆形为种群中不同的个体,不同的颜色代表着不同的Pareto等级. 图3 Pareto等级示意图 Fig.3 Grade diagram of Pareto 设种群中每个个体Xi被其他个体支配的个体数目为Ni,被Xi支配的个体的集合为Si,令各级非支配层所包含的个体集合为Fi. 算法的主要步骤为:①找到种群中Ni=0的个体,并保存在当前集合Fi中;②对于当前集合Fi中的每个个体i,其所支配的个体集合为Si,遍历Si中的每个个体j,执行Nj=Nj-1,如果Nj=0,则将个体j保存在集合Fj中③记F1中得到的个体为等级为1的非支配层个体,重复上述操作,直到整个种群被分级.非支配层快速建立算法伪代码如算法I所示. 算法I 快速非支配排序算法输入:种群中每个个体Xi及其目标分量{fXi ,g(Xi)}.输出:各级非支配层所包含的个体集合Fi.1: 计算每个个体Xi被其他个体支配的其他个体数目Ni.2: 计算每个个体Xi支配的其他个体的集合Si.3: for i∈1,…,n then4:ifNi==0 then5:F1←F1∪Xi;6:end if7:end for8:while i∈1,…,n then9:for Xj∈Fi&&j∈{1,…,n} then10:for Xz∈Sj&&z∈1,…,n then11:Nz←Nz-1; 12: if Nz==0 then13:Fi+1←Fi+1∪Xz;14:end if15:end for16:end for10:end while 在NSGA-Ⅱ多目标优化算法中,引入聚集距离对同一非支配层中的个体进行排序,充分保证个体能均匀分配在Pareto前沿,保证选取的某一非支配层中个体的多样性. 定义每个个体的拥挤距离为Di,其中Di表示个体Xi在同一层相邻的两个体Xi+1和Xi-1中,对应目标值的差值总和,如公式(2)所示. Di=|F(Xi+1)-F(Xi-1)|+|G(Xi+1)-G(Xi-1)|. (2) 通过快速非支配排序和拥挤度计算之后,种群中的每个个体i都得到两个属性:非支配排序nrank和拥挤度Di.利用这两个属性,可以区分种群中任意两个个体的支配与非支配关系.定义一个偏序n如下:如果irank 如图4所示,个体i的拥挤距离即为该个体在同一非支配层中相邻的两个个体中组成最大矩形的边长的一半,当该值越大时,个体分布越分散,该个体在该非支配层中的排序越高. 图4 拥挤距离图形化示意图Fig.4 Graphical diagram of crowding distance 2.5.1 插入算子如图5所示,设u,v为路径上相邻两点,若存在一个不在当前路径上的点p,u可以直接到达p,p也可以直接到达v,此时称p为可插入的.对一条路径执行插入算子的步骤如下:寻找任意两相邻点的所有可插入点,在可插入点不为零的所有位置中,随机确定一个位置,然后再在此位置的所有可插入点中随机选择一个点插入. 图5 插入算子示意图Fig.5 Schematic diagram of insertion operator 2.5.2 删除算子如图6所示,设u,p,v为路径上相邻的3个点,若u可以直接到达v,此时称p为可删除的.对一条路径执行删除算子的步骤如下:确定路径上哪些点是可删除的,再随机选择一个删除. 图6 删除算子示意图Fig.6 Schematic diagram of deletion operator 2.5.3 替换算子如图7所示,设u,p,v为路径上相邻的3个点,若存在一个不在当前路径上的点q,u可以直接到达q,q可以直接到达v,则称p是可替换的.对一条路径执行替换算子的步骤如下:先确定路径上的哪些点是可替换的,随机选择一个可替换点x,找出所有不在当前路径上且能替换x的点,再随机选择一个替换x. 图7 替换算子示意图Fig.7 Schematic diagram of substitution operator 如图8所示,精英策略是选择优秀下一代父代的方式,通过对此时种群进行快速非支配层排序并按拥挤距离在同一非支配层进行个体优劣排序,选择非支配层等级高、聚集距离大的个体遗传到下一代中,充分保证下一代的父代个体的优劣性. 图8 精英选择策略示意图Fig.8 Schematic diagram of elite selection strategy ①首先读取图数据,以邻接表的形式存图,执行种群初始化,P,Q两种群分别生成种群中的有效路径,生成完毕合并到种群R; ②对种群R进行非支配排序并计算每一非支配层个体的拥挤距离,筛选个体进入下一代P种群P2,直至P2大小达到上限,对P2执行遗传操作,锦标赛选择个体,根据初始设定的各遗传算子的作用概率来决定其是否进行插入,删除和替换; ③P2经过遗传操作后产生的所有个体的集合即为下一代Q种群Q2,P2和Q2合并产生种群R2重新进行非支配排序; ④循环执行①、②、③步骤,直至进化代数达Gen到初始设定的最大进化代数Genmax,最终P种群中的所有非支配个体即为问题的最优解. 本测试数据来源于高德地图,选取的是株洲市区某一小块区域,起点是湘水栗园左旁的路口(标号0),终点是株洲市中心医院(标号61),测试数据中的时间表示车辆行驶这条道路的预计花费时间,已考虑道路上的交通信号灯数目和道路类型. 图9 区域地图 图10 区域模型图 Fig.9 Regional map Fig.10 Area model diagram 图10是根据图9建立的一个模型图,选取一些道路的交叉点作为图的顶点,道路作为图的边,其中顶点0为出发点,顶点61为株洲市中心医院所在点. 表1 区域道路信息表Tab.1 The informatiion of regional road 表1(续) 对于种群大小,较大的种群可以增强算法的寻优能力,但也会增加程序的计算量,降低程序的运行速度.最大进化代数需要估计算法的期望收敛代数,选择尽量小的最大进化代数的同时尽可能的保证算法的收敛性.插入概率影响着路径的加长,而删除概率影响着路径的缩短,当插入概率远大于删除概率时,搜索会朝着长路径的方向进行,当删除概率远大于插入概率时,搜索会朝着短路径的方向进行,当插入概率和删除概率相差不大时,搜索均匀的朝长路径和短路径方向扩展.替换概率不宜过大,过大的替换概率会使算法的随机性变大,同时增加了程序的计算量.本次测试的初始参数设定如表2所示. 表2 初始参数设置Tab.2 The setup of initial parameters 最终种群中去除重复个体后得到的最优解如表3所示. 表3 最优解路径信息Tab.3 The information of optimal solution route 最优解均满足Pareto非支配关系,如最优路径1和最优路径2,虽然最优路径1的路程比最优路径2短0.07 km,但是最优路径1需要花费的时间比最优路径2多0.44 min. 对图进行深度优先遍历,搜索出图上所有起点到终点的合法路径,在所有合法路径中筛选出最优解,得到的结果与使用NSGA-Ⅱ算法求得的完全相同. 除此之外我们还对最优解的收敛性进行了研究,结果如图11与图12所示,不同迭代次数的PF分布情况如图13所示.图14、图15展示了不同代数情况下的GD与IGD值. 图11 预计路程收敛情况 图12 预计时间收敛情况 Fig.11 Convergence of estimated distance Fig.12 Estimated time convergence 图13 不同代数情况下的Pareto FrontFig.13 Pareto Front of different algebraic 图14 不同代数情况下的GD 图15 不同代数情况下的IGD Fig.14 GD of different algebraic Fig.15 IGD of different algebraic 本文从生活中常见的单目标路径寻优问题出发,延伸出多目标的路径寻优即多目标导航问题,并利用计算机图论的相关知识,建立了问题的图论模型.考虑到问题解空间规模的庞大,无法通过常规的多项式算法求解,转而运用人工智能领域的智能算法,最终采用多目标进化算法中非常流行的NSGA-Ⅱ算法解决了此问题. 各大主流导航软件在寻找最优路径时虽然综合考虑了各方面条件并给用户提供了多种选择方案,用户也可以根据其中的某个条件排序选择自己想要的方案,但是用户无法同时指定多个自身需要的条件,即导航软件不能根据用户的需求进行多个目标的导航.其次,导航软件的智能寻优能力还有待加强,避免导航出非最优或非法的路线.相信随着科学技术的发展,导航系统的功能将更加强大,给人类的出行带来更大的便利.

2.3 非支配层快速建层算法

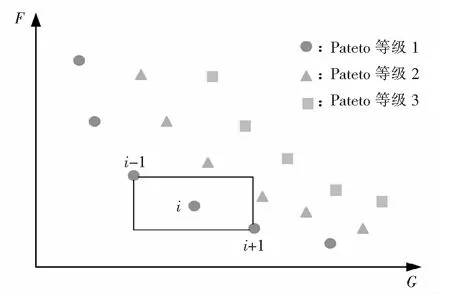
2.4 同一非支配层中拥挤距离的计算
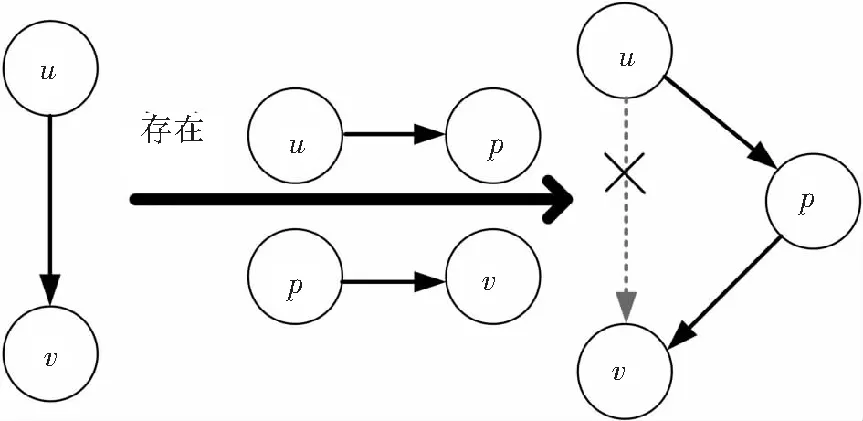
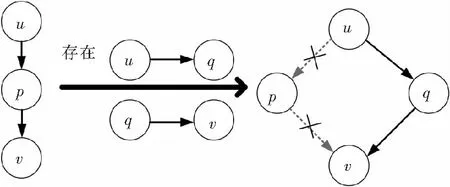
2.5 遗传算子的设计

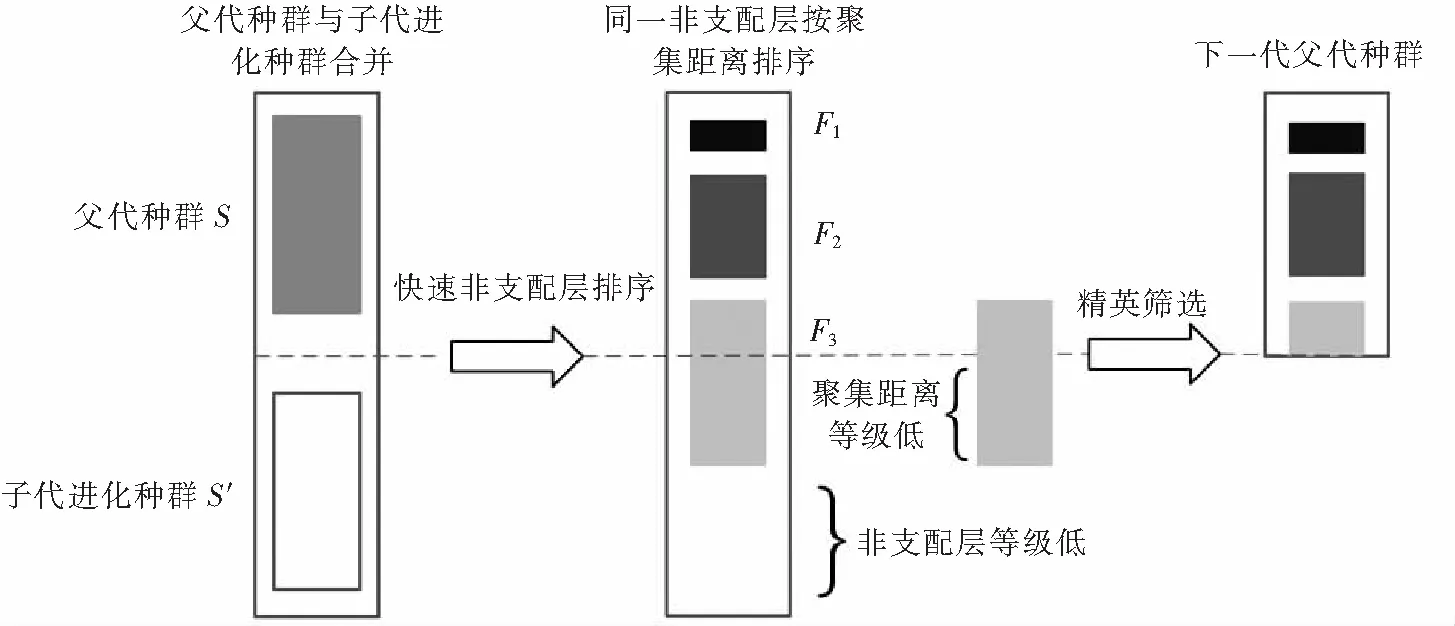
2.6 锦标赛选择与精英策略
2.7 算法整体流程
3 实验与分析
3.1 实验场景


3.2 初始参数设定

3.3 结果与分析




4 结论
