基于动力响应互相关的古建筑木结构损伤识别
2022-01-27侯艳芳杨泽华胡卫兵
侯艳芳,杨泽华,胡卫兵,郭 靖
(1.西安建筑科技大学 土木工程学院, 陕西 西安 710055;2.陕西工业职业技术学院 土木工程学院, 陕西 咸阳 712000;3.郑州职业技术学院 建筑工程系, 河南 郑州 450121)
0 引言
中国古建筑是人类珍贵的文化遗产,忠实而客观地反映了历史发展的脉络及面貌,甚至保存了许多文字无法记录的史料,蕴含了浩瀚无涯的精神文化。中国古建筑内涵深厚而形神皆备,它具有许多特质,在技术方面善于运用木结构,将木材技术发挥到极致,为世界其他文明所罕见[1]。古建筑木结构在千百年的使用过程中,历经风雨侵蚀,受材料老化及长期荷载效应等灾害因素的共同作用,存在不同程度的损伤和破坏。现代地面交通和城市轨道交通引起的微幅振动使古建筑受到持续的损伤,将不可避免地出现系统的损伤积累和抗力衰减,从而导致抵抗自然灾害甚至正常环境作用的能力降低,给结构的安全性带来了隐患。古建筑被誉为“立体的教科书”和“现成的博物馆”,一旦消失不可复得。若能通过一定的方法,对木结构古建筑进行有效的损伤识别和安全性评定,及时发现和控制结构的损伤,对古建筑的修缮和保护具有重要意义。
近年来,利用环境激励荷载对结构进行损伤识别成为结构健康监测中损伤检测的热点[2-4]。杨智春等[5]提出了基于互相关函数幅值向量和连续小波变换联合检测损伤的方法。于哲峰等[6-8]利用结构在随机激励下某点响应与其他各点响应之间的互相关函数,提出了互相关函数幅值向量的概念,进行了基于互相关函数幅值向量的受随机激励结构损伤检测的实验研究及损伤定位方法研究。
1 互相关函数的基本原理
对于一个随机振动过程,若有两个不同的随机函数x(t)和y(t),它们之间的互相关函数定义为[9]
Rxy(τ)=E[x(t)y(t+τ)】。
(1)
互相关函数描述的是x(t)和y(t)在任意两个不同时刻t和t+τ取值之间的相关程度。若x(t)和y(t)是离散型随机序列,则两个信号相对移动τ值后的互相关函数值为
(2)
式中,Rxy(τ)是τ的函数。当τ=τ′时,R(τ)取得最大值,此时信号x(t)和y(t)最为相似,相关性最高。其中,τ表示两个信号的相对移动值,即是时间坐标t的移动值,而不是指时间。特殊的情况,当τ=0时,表示一个信号对另一个信号不移动,也就是把两个波形对应的纵坐标相乘再相加,即:
(3)
若信号是连续函数,取样间隔为Δt,即:
(4)
将式中的Δt取得非常小,或者是N→∞,则可以用dt表示Δt,前面的求和公式就变成了积分形式,则有
(5)
其中:T为测量信号的时间长度,τ为时间间隔。
据资料显示,我国政府有出台相关条例和通知要求高校加强对大学生应急救护教育。早在1990年,我国教育部及卫生部就在《学校卫生工作条例》中指出“学校应当把健康教育纳入教学计划,普通高等院校应当开设健康教育选修课或讲座”;2014年,江苏省教育厅发布了《关于实施我省百万大学生应急救护提升行动的通知》。政府在医疗改革方面也注意到了应急救护的重要性,《江苏省深化医药卫生体制改革规划(2018-2020年)》文件中关于重点任务里提及要健全完善医疗卫生服务体系,其中落实急救等医疗卫生事业专项规划,以及要进一步完善卫生应急体系。
受随机振动的结构,若在一段时间内同时测得结构上n个测点的振动响应信号,则某测点i的响应信号xi(t)与其他各测点响应信号xj(t) (j=1,2,…,n)之间的互相关函数Rij(τ)可由式(2)计算得到。设Rij(τ)在τ=τ′处取得最大值,记为Rij(τ′)=kij。将所有的最大值组成一个以i为参考点的互相关函数峰值向量,记为CCPV:
CCPV=[ki1,ki2,…,kin],
(6)
表示两组信号相关程度的一个重要特征数值是互相关系数[10]:
(7)
式中:cov(x,y)为x和y的协方差;σx和σy为x和y的标准差;μx和μy为x和y的均值。
互相关系数ρxy表达的是两组信号或向量之间的相关程度,其大小能够直接反映出所描述的两个信号之间的相关程度,取值范围为[0,1]。当x(t)=y(t)时,即信号与自身相关时,ρxy=1;当x(t)和y(t)不相关时,ρxy=0。
互相关系数越大,相关程度就越高;反之,ρ值越小,也就说明两组向量之间的相关性越小。因此,可以根据两组互相关峰值向量之间的互相关系数的大小,判别结构是否发生了损伤,即可以将互相关系数作为结构损伤识别的损伤因子。
2 算例分析
2.1 建立有限元模型
中国古建筑木结构类似于现代的框架结构,但区别于现代钢结构、钢筋混凝土结构的一个显著特点是梁和柱通过榫卯节点连接。榫卯连接中,榫有一定的长度,榫卯结构之间有一定的间隙,因此该连接方式并非刚接,也非铰接,而是介于刚接和铰接之间的半刚性连接[11-13]。基于榫卯节点的这种半刚性特点,建立有限元模型时,采用combin14弹簧单元模拟梁柱的榫卯连接,在梁和柱的连接位置设置多个重合的有限元节点,如图1所示。图1中节点①代表柱端,②、③、④、⑤分别代表与之相连接的梁端,仅在梁和柱榫卯连接的位置施加弹簧单元,柱与柱之间不再施加弹簧单元。每个榫卯节点共有6个方向的自由度,其中3个平动自由度UX、UY、UZ和3个转动自由度ROTX、ROTY、ROTZ。柱端节点和梁端节点采用6个弹簧单元进行模拟,再设置梁柱各个自由度方向的弹簧刚度参数,以此实现梁柱的榫卯连接。
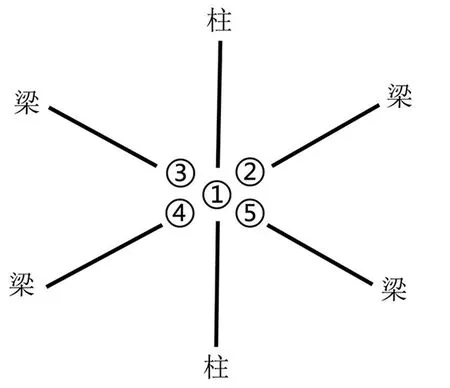
图1 梁柱的榫卯连接Fig. 1 Mortise-tenon joint between beams and columns
建立木框架有限元模型时,以西安钟楼为工程背景,选取梁、柱的尺寸。其中,木柱为圆柱,高6 m,截面直径500 mm;木梁长度为4 m,截面尺寸300 mm×700 mm;梁柱采用三维弹性单元beam188单元模拟。采用文献[14]中实测的木材材料参数,见表1。

表1 木材的材料参数Tab. 1 Material parameters of wood
采用Rayleigh定义的黏性比例阻尼。榫卯节点刚度采用文献[15]中根据钟楼监测数据得到的近似值:1×1010kN·m/rad。木框架有限元模型及节点编号如图2所示。
随机激励选择文献[16]中西安地铁单线运行时,速度为分别V1=20 km/h和V2=40 km/h时的荷载值作为激励荷载1和激励荷载2施加在柱脚节点上,激励时长取T=12 s,时间步长为Δt=0.01 s。
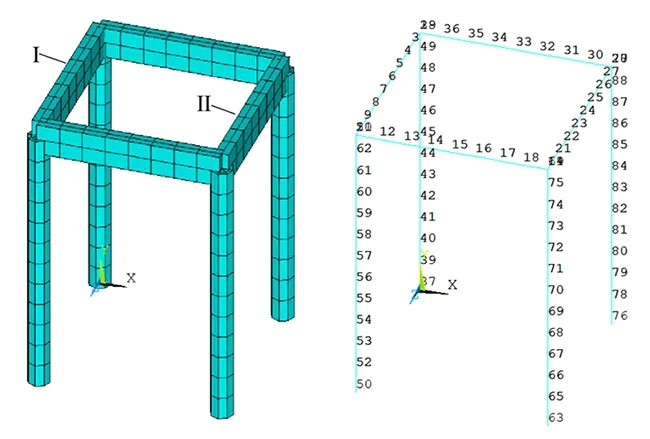
图2 有限元模型及节点编号Fig. 2 Finite element model and nodes number
2.2 结构的损伤识别
选取木框架上Ⅰ号梁为研究对象,节点编号为3~9,对应的单元为②~⑦。为了方便后文的表达,将节点重新编号为1~7,对应的单元编号为①~⑥。提取各节点的加速度响应,选择节点4作为参考点,计算其他各点与参考点之间的互相关函数。以节点3为例,节点3和节点4加速度响应之间的互相关函数如图3所示。
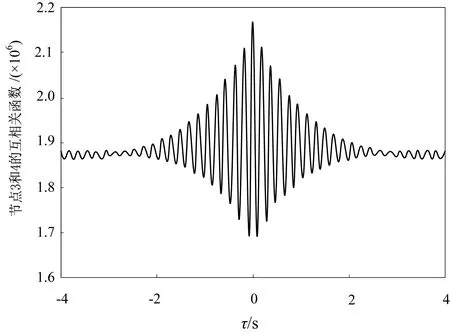
图3 节点3和4加速度响应之间的互相关函数Fig. 3 Cross-correlation function between acceleration responses of nodes 3 and 4
从图3中可以看出,节点3和节点4加速度响应之间的互相关函数在τ=0处取得最大值,这是因为此时信号就是与自身求相关,相关程度最大。将所有的最大值组成互相关峰值向量。完好结构在两个激励荷载作用下,以节点4为参考点的加速度响应的互相关峰值向量分别记为C1和C2,绘制C1和C2的曲线,如图4所示。
由此可见,完好结构在两个频谱稳定的随机荷载作用下,梁上各测点与参考点之间加速度响应的互相关峰值向量曲线具有相似的形状,说明互相关峰值向量具有固定的形态。因此,采用互相关峰值向量构建结构损伤识别指标具有可行性。利用式(7)计算C1和C2之间的互相关系数,结果如表2所示。
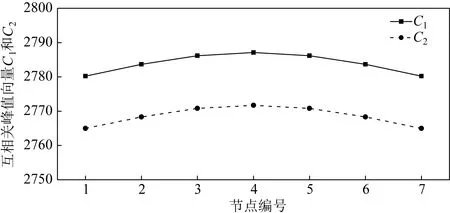
图4 激励荷载1和2作用下完好结构的CCPVFig. 4 CCPV of intact structure under loads 1 and 2

表2 C1和C2之间的互相关系数Tab. 2 Cross correlation coefficient of C1 and C2
可以看出,两个完好结构之间的互相关系数以极小的误差接近于1,说明两组向量之间具有较高的相关性。将完好结构C1和C2之间的互相关系数ρ12=0.999 999 99作为损伤识别的基准值,若再次测得的峰值向量与完好结构峰值向量之间的互相关系数明显小于基准值,则可判别结构发生了损伤。
通过降低单元刚度模拟结构的损伤。依次将Ⅰ号梁上①~⑥各单元的刚度降低30%,利用式(2)计算各单元分别发生损伤时,损伤结构上的各测点与参考点4加速度响应之间的互相关峰值向量,将损伤结构的峰值向量记为Cs,选择C1作为完好结构的峰值向量,记为Ch。各单元分别出现损伤时,损伤结构的Cs和完好结构的Ch之间的互相关系数ρsh如表3所示。
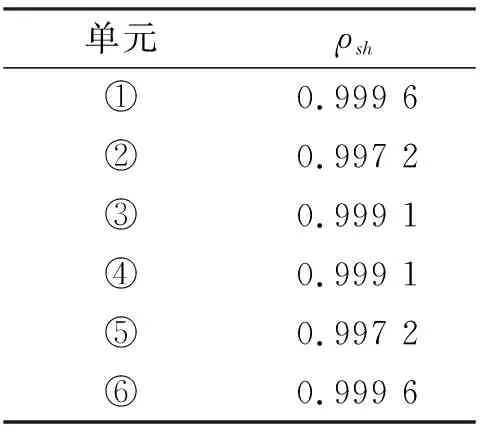
表3 各单元分别损伤30%时与完好结构之间的ρshTab. 3 ρsh between damaged 30% and intact structure
从表3中可以看出,当结构出现损伤时,损伤结构与完好结构互相关峰值向量之间的互相关系数明显小于基准值,说明损伤结构的Cs和完好结构的Ch之间的相关性降低,由此可以判断结构发生了损伤。因此,通过互相关系数构建的结构损伤因子,可以有效识别结构的损伤。
2.3 损伤定位分析
结构出现损伤后,损伤结构和完好结构之间的相关性会降低,也就是向量中各个元素发生了变化。为了衡量结构损伤前后互相关峰值向量中各元素的变化程度,计算损伤前后各测点互相关峰值的变化率,即:
(8)
当梁上①~⑥单元分别出现损伤时,计算互相关峰值向量中各元素损伤前后的相对变化,为了方便绘图和表达,将各变化率的绝对值按最大值做归一化处理,如图5所示。
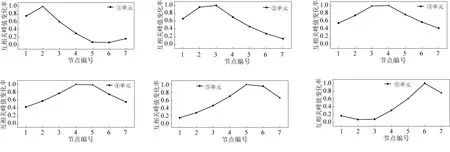
图5 各单元损伤时的峰值变化率Fig. 5 Peak change rate under each damaged unit
从图5中可以看出,当某个单元出现损伤时,与该单元对应的两个节点的互相关峰值的变化率最大。如当单元③损伤时,结构损伤前后峰值变化率最大的相邻两个节点就是该单元两端的节点3和节点4。其他单元发生损伤时,也满足这种对应关系。因此,可以利用结构上各测点动力响应互相关峰值向量中各元素损伤前后的变化率来确定结构的损伤位置,即结构损伤出现后,互相关峰值变化率最大的相邻两个测点所对应的区域即是结构的损伤位置。
2.4 损伤程度的估计
为了观测不同的损伤程度对损伤因子(互相关系数)和损伤指标(峰值变化率)的影响,以单元⑤为例,依次将单元刚度降低5%、10%、20%、30%,对应的损伤因子的数值以及与基准值相比较的相对变化值如表4所示。
从表4中可以看出,当损伤程度为5%即结构轻度损伤时,结构损伤前后互相关系数的变化范围仅为0.02‰;当结构损伤程度为10%时,损伤前后互相关系数的变化为0.07‰以内;当结构出现20%的损伤时,互相关系数的变化范围为0.33‰,与损伤程度为10%的变化范围相比,有明显的提高,且增幅较大;当结构出现30%的损伤时,损伤前后损伤因子的变化范围已接近0.90‰。因此,可以根据结构损伤前后互相关系数的变化范围估计结构的损伤程度。与损伤因子相似,不同的损伤程度,损伤前后各节点互相关峰值变化率的数值范围也不同。当单元③分别损伤5%、10%、20%和30%时,各节点的峰值变化率如图6。
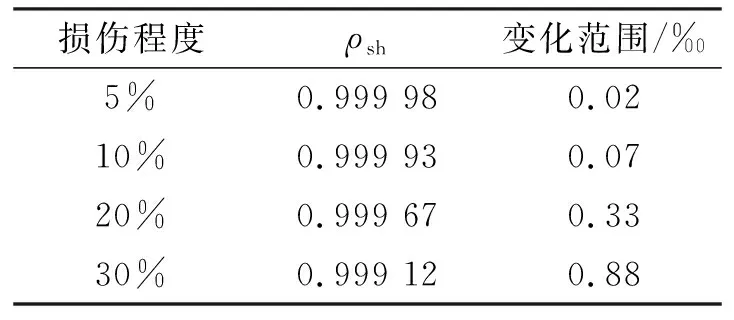
表4 不同损伤程度下的ρsh及变化范围Tab. 4 ρsh and change rate in different degrees of damage
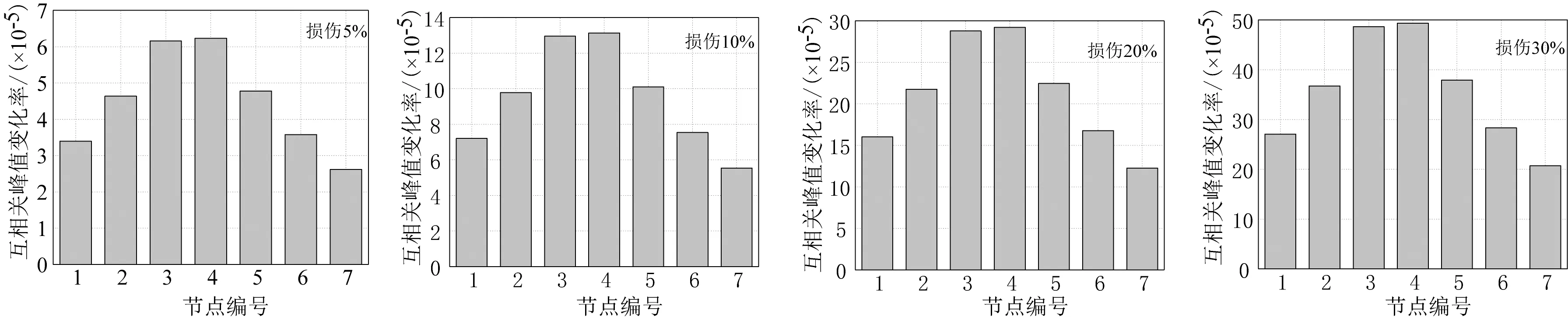
图6 不同损伤程度下的峰值变化率Fig. 6 Peak change rate in different degrees of damage
从图6中可以看出,当单元③出现不同程度的损伤时,都满足损伤前后互相关峰值变化率最大的相邻两个节点对应着损伤单元两端的节点。损伤5%时,节点3和4的变化率明显高于其他各点,说明以结构损伤前后动力响应互相关峰值变化率构建的损伤识别指标,能够识别结构的初期损伤,具有较好的损伤敏感性。不同的损伤程度下,各节点损伤前后互相关峰值变化率的形态相似,但纵坐标的数值却有明显的不同。因此,可以根据损伤前后互相关峰值变化率的数值范围估计结构的损伤程度。
3 结论
通过降低结构构件的刚度模拟结构的损伤,利用互相关系数和互相关峰值变化率对古建筑木结构进行损伤识别和定位,结果表明:
(1)将两组完好结构的互相关峰值向量之间的互相关系数作为损伤因子的基准值,结构出现损伤后,互相关系数的数值明显降低,因此使用损伤因子能够有效识别结构的损伤;
(2)以结构损伤前后动力响应互相关峰值的变化率构建损伤识别指标,峰值变化率最大的相邻两个测点对应着损伤单元的两个节点,能够准确确定结构的损伤位置;
(3)不同损伤程度下,损伤因子和峰值变化率的变化范围不同,可以根据损伤前后对应数值的变化范围估计结构的损伤程度。
