负载特性对地震模拟振动台控制性能影响分析
2022-01-27高春华王洁琼张永河袁晓波
高春华,王洁琼,张永河,袁晓波
(信阳师范学院 建筑与土木工程学院, 河南 信阳 464000)
0 引言
目前,地震模拟振动台控制算法将试件与台面看成一个整体,即将试件看作是完全刚度,也就是说,无论哪种试件与空台的区别就在于增加了台面质量而已[1]。但实际中,往往试件的特性与振动台本身的特性具有较大的差异,台面的自振频率一般为20 Hz左右,而实际工程中一般试件的频率在2~8 Hz。国内外许多学者已对该问题进行了不同程度的研究,BLONDET等[2]、CREWE等[3]从理论和试验两个方面对其进行了相关研究,频率不同的试件对地震模拟振动台波形再现精度具有较大的影响;DYKE等[4]在结构主动控制研究中考虑了控制-结构相互作用对系统控制性能的影响,建立了作动器-结构相互作用模型。KAJIWARA等[5]、MAOULT等[6]针对试件与振动台台面的边界条件进行了有限元分析,验证了台面与试件相互作用的影响。CREWE等[7]、TWITCHELL等[8]对其进行对比试验研究,试验结果表明试件对振动台的影响不可忽视。我国学者也相继进行了研究,李暄等[9]通过对N个自由度的试件作用下振动台系统的理论分析指出:当振动台振动强度较大时,试件的非线性性质对振动台系统传递函数影响较大,台面振动再现精度降低;提高台面质量与试件质量之比是提高台面振动再现精度的方法之一,只有当试件质量远小于台面质量时才可忽略试件对系统性能的影响。唐贞云等[10]对试件特性对地震模拟振动台控制性能的影响进行了相应的研究,得出了试件对地震模拟振动台性能影响较大,同时给出了补偿措施,但是该研究针对固定的试件,不具备通用性。李芳芳等[11]对消除试件对系统控制的影响,提出了力反馈补偿算法,提高了试验精度。各种算法的研究对象不同,适用范围也不同,故地震模拟振动台性能影响有待于进一步深入研究。
本文针对以上问题综合考虑地震模拟振动台系统性能的情况下,分析负载特性对地震模拟振动台控制精度的影响,并提出了压差反馈补偿算法,大大提高了地震模拟振动台的波形再现精度。
1 单自由度负载的液压系统分析
假定台面上试件为惯性质量块-单自由度负载,系统可简化为图1所示。
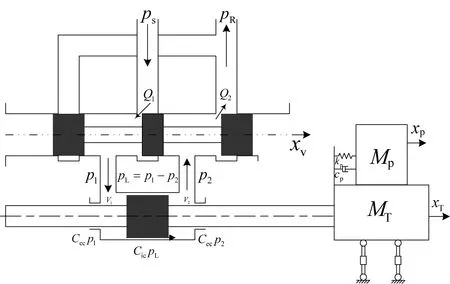
图1 单自由度负载的电液伺服地震模拟振动台Fig. 1 Diagram of electro-hydraulic servo valve considering single degree of freedom
根据液压三连续方程,以试件为研究对象可得:
Mps2xp+cpsxp+kpxp=-Mps2xT,
(1)
式中:Mp为试件质量;cp为试件阻尼系数;kp为试件刚度系数;xp为试件相对台面的相对位移;xT为台面位移;s为拉普拉斯积分算子。
由式(1)可得试件相对位移xp与台面位移xT间的传递函数可以表示为
(2)
由图1可知xTp=xT+xp,根据式(2)可知试件绝对位移xTp与台面位移xT间的传递函数可表示为
(3)
式中:ξp为阻尼比;fp为固有频率。
试件对地震模拟振动台台面的反力可表示为
FTp=-Mps2xTp=-MpHp(s)s2xT。
(4)
地震模拟振动台台面的受力可表示为
[MT+MpHp(s)]s2xT=AppL,
(5)
式中:MT为台面质量;pL为负载压力;Ap为活塞有效承压面积。
由以上分析可知,惯性质量块作用下的地震模拟振动台三连续方程可表示为:
(6)
式中:QL1为作动缸所需流量,QL2为伺服阀所需流量,V为控制腔的体积,β为液体体积弹性模量,Cc为液压缸的泄露系数,QL为负载流量,kq为包括阀控器在内的电压流量增益,Kc为滑阀在稳态工作点附近的流量压力系数。式(6)方块图如图2所示。
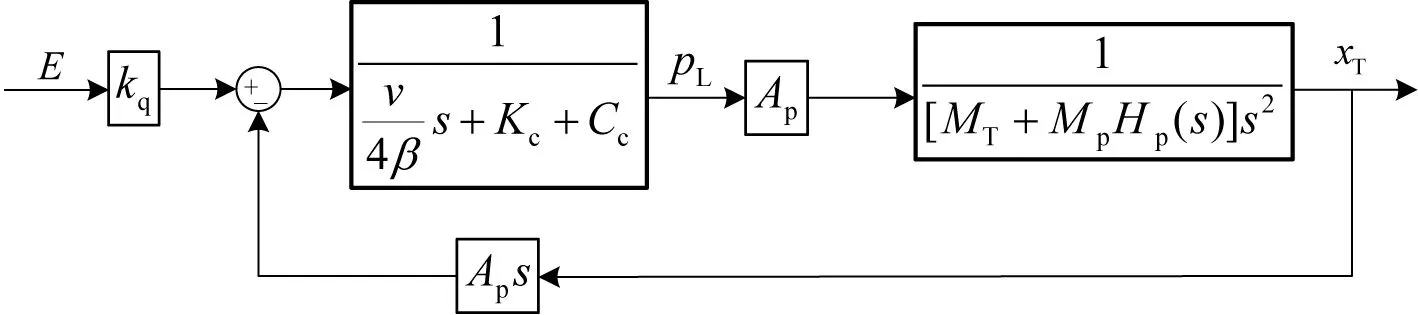
图2 考虑单自由度负载的系统传递函数图Fig. 2 Diagram of system transfer function considering single degree of freedom
台面位移xT与系统的驱动信号E间的传递函数可表示为
(7)
式中:Me为试件与台面等效质量,Me=MT+MpHp(s)。
根据式(7)传递函数,采用Matlab仿真模拟空载、刚性负载及单自由度负载作用的系统传递函数的频响特性图3所示。
从图3可以看出:单自由度系统的频响特性与空载作用下的频响特性较为接近,也就是说考虑单自由度负载时,采用空载参数比采用刚性负载时参数的控制精度要高。
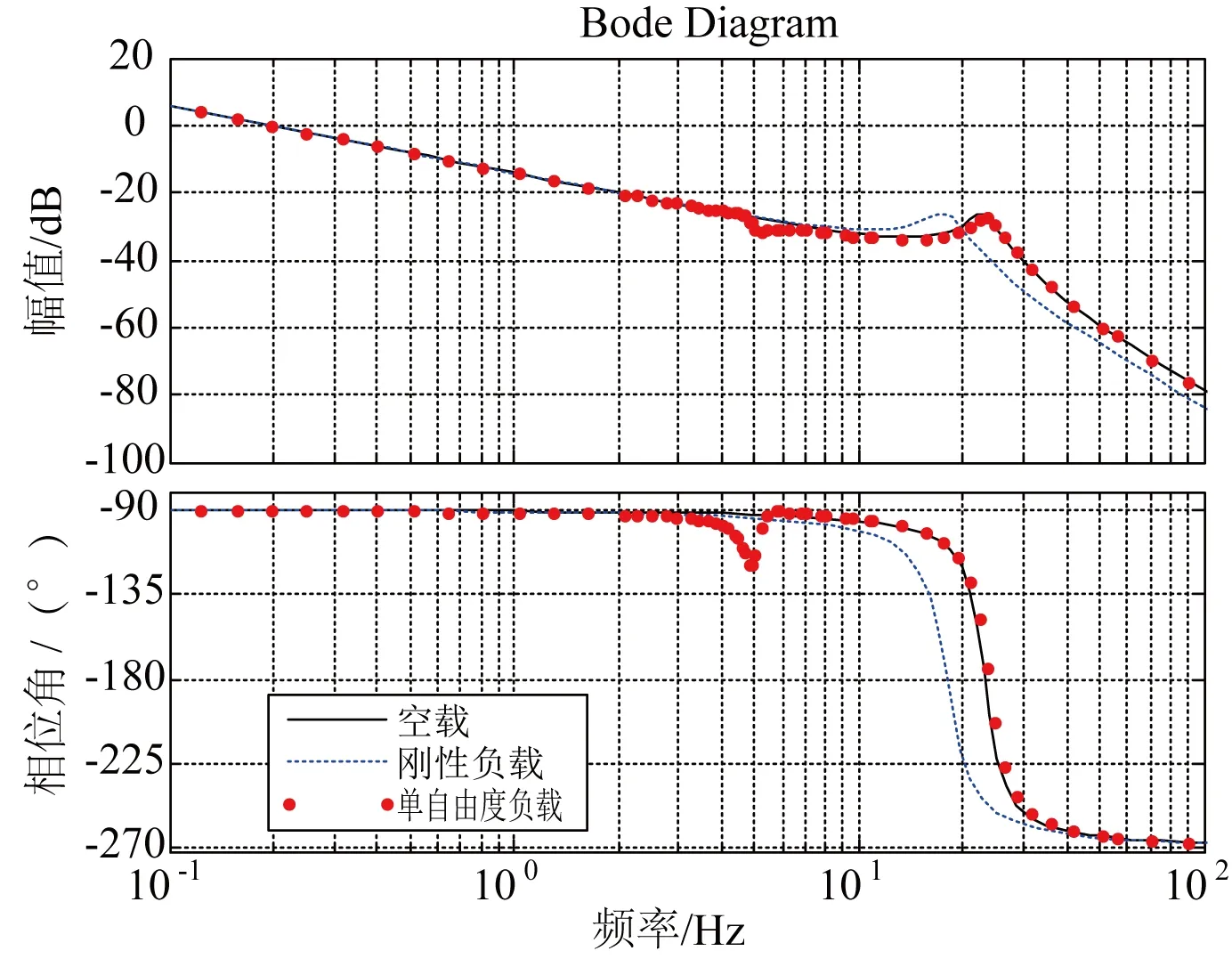
图3 系统传函频响特性曲线Fig. 3 Frequency response characteristic curve of system
2 三参量控制下单自由度负载与台面的共同作用分析
三参量控制主要是由反馈控制和前馈控制两部分组成,反馈控制同样也采用位移、速度和加速度反馈控制。通过反馈控制提高了地震模拟振动台的使用频宽同时减小波形失真度,还可以保证系统的稳定性。通过调节加速度反馈增益的大小,来改变系统阻尼的大小,实现削低油柱共振峰的作用,从而可以扩宽使用频率范围,同时系统仍然保持稳定。三参量控制示意图如图4所示。

图4 三参量控制示意图Fig. 4 Three parameter control
考虑单自由度负载的液压系统的基础上引入三参量反馈,系统的传递函数方块图如图5所示。
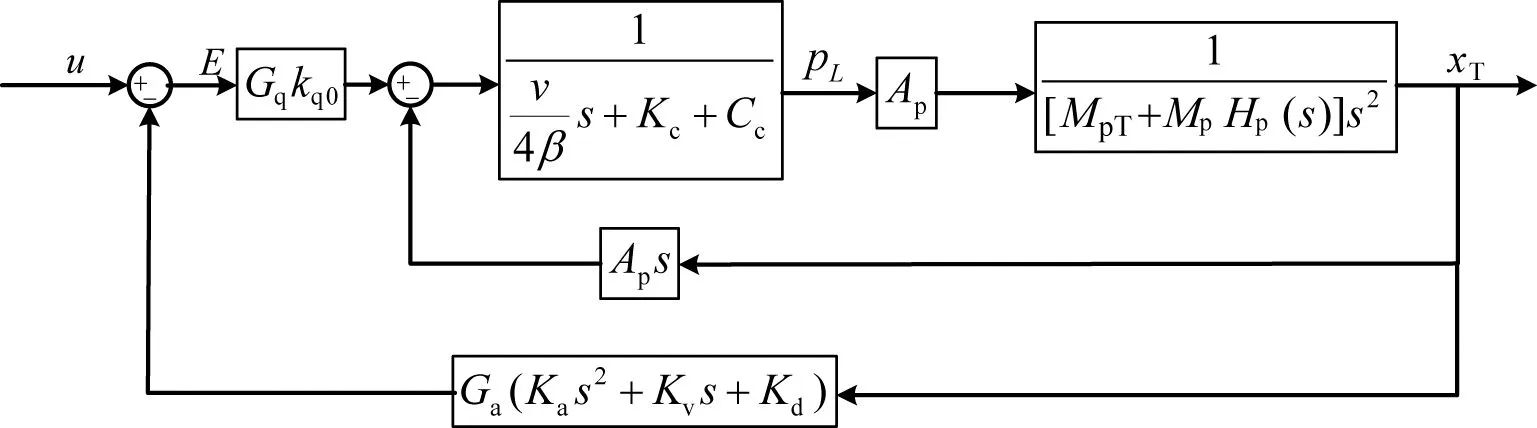
图5 考虑单自由度负载的系统传递函数图Fig. 5 Diagram of system transfer function considering single degree of freedom
传递函数可以表示为:
(8)
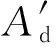
2.1 不同参数下系统特性比较
2.1.1 满载情况下系统特性
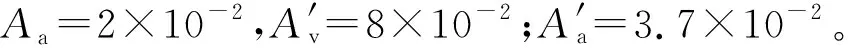

图6 刚性负载参数考虑试件的系统传函频响特性曲线Fig. 6 Frequency response characteristic curve of shaking table with specimen based on rigid load parameters
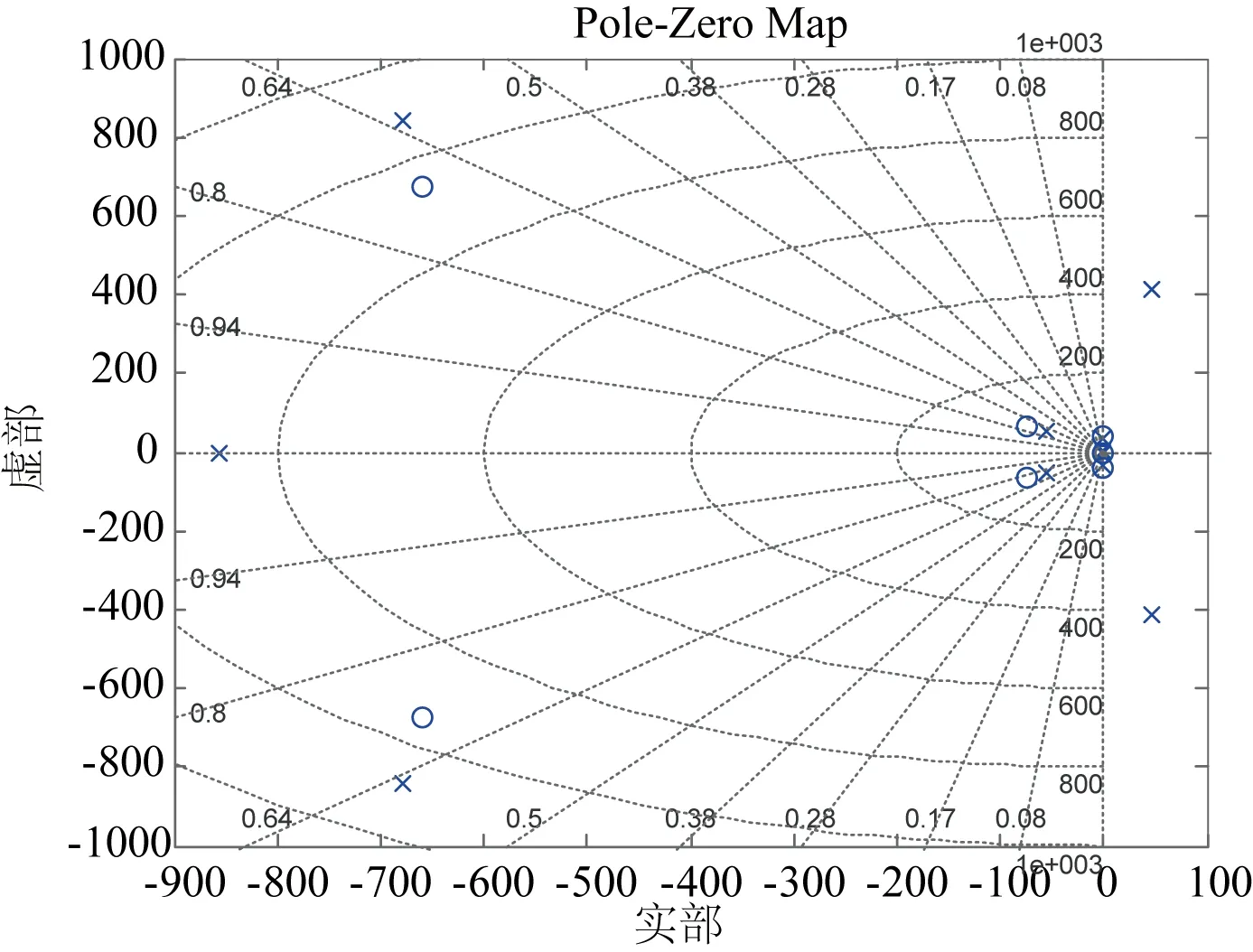
图7 刚性负载参数考虑试件的系统极点坐标图Fig. 7 Pole-zero map of shaking table with specimen based on rigid load parameters
从图6、图7可以看出:刚性负载参数不考虑单自由度负载的系统频带在0.4~50 Hz范围内;刚性负载参数考虑单自由度负载的系统在试件自振频率处有一峰谷,在高频区域内有共振峰,同时在峰谷处的相位有波动,在高频区域相位向正值变化,系统不稳定;从极点图可以看出,刚性负载下具有右半平面的极点(图中“x”代表极点,“o”代表零点),系统是不稳定的。
2.1.2 空载情况下系统特性
从图8、图9可以看出:空荷参数考虑单自由度负载的系统在试件共振频率处有一峰谷,在高频区域系统特性仍较为理想,系统处于稳定状态。从极点图也可以看出,系统的极点均位于左半平面内,系统是稳定的。

图8 空荷参数考虑试件的系统传函频响特性曲线Fig. 8 Frequency response characteristic curve of shaking table with specimen based on empty load parameters
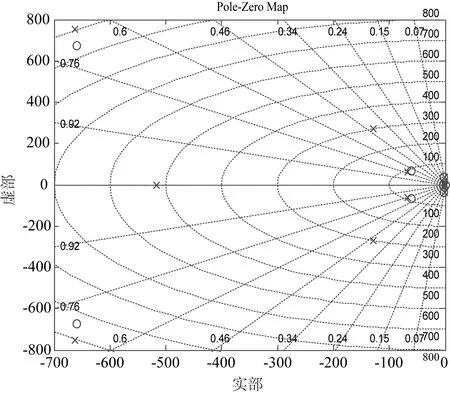
图9 空荷参数考虑试件的系统极点坐标图Fig. 9 Pole-Zero map of shaking table with specimen based on empty load parameters
以上分析可以看出,进行地震模拟振动台试验时,考虑弹性负载的情况下,空荷参数设置的系统控制效果优于刚性负载参数设置的系统。
2.2 试件特性对系统性能的影响分析
为保证系统的稳定性,地震模拟振动台所有负载的情况下均采用空载设计参数,试件-振动台系统的自振频率分别为5、5、5 Hz;阻尼比为0.01、0.03、0.05,试件质量分别取0.5、1.0、1.5倍,考虑单自由度弹性负载的系统频响特性如图10、11、12所示。
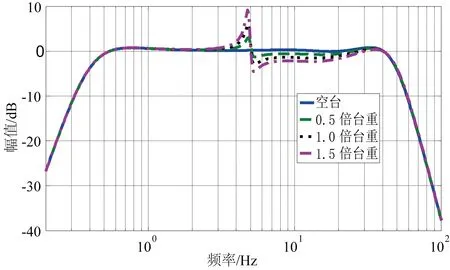
图10 不同质量单自由度负载振动台频率特性(5 Hz)Fig. 10 Frequency Response of shaking table with different mass SDOF payload
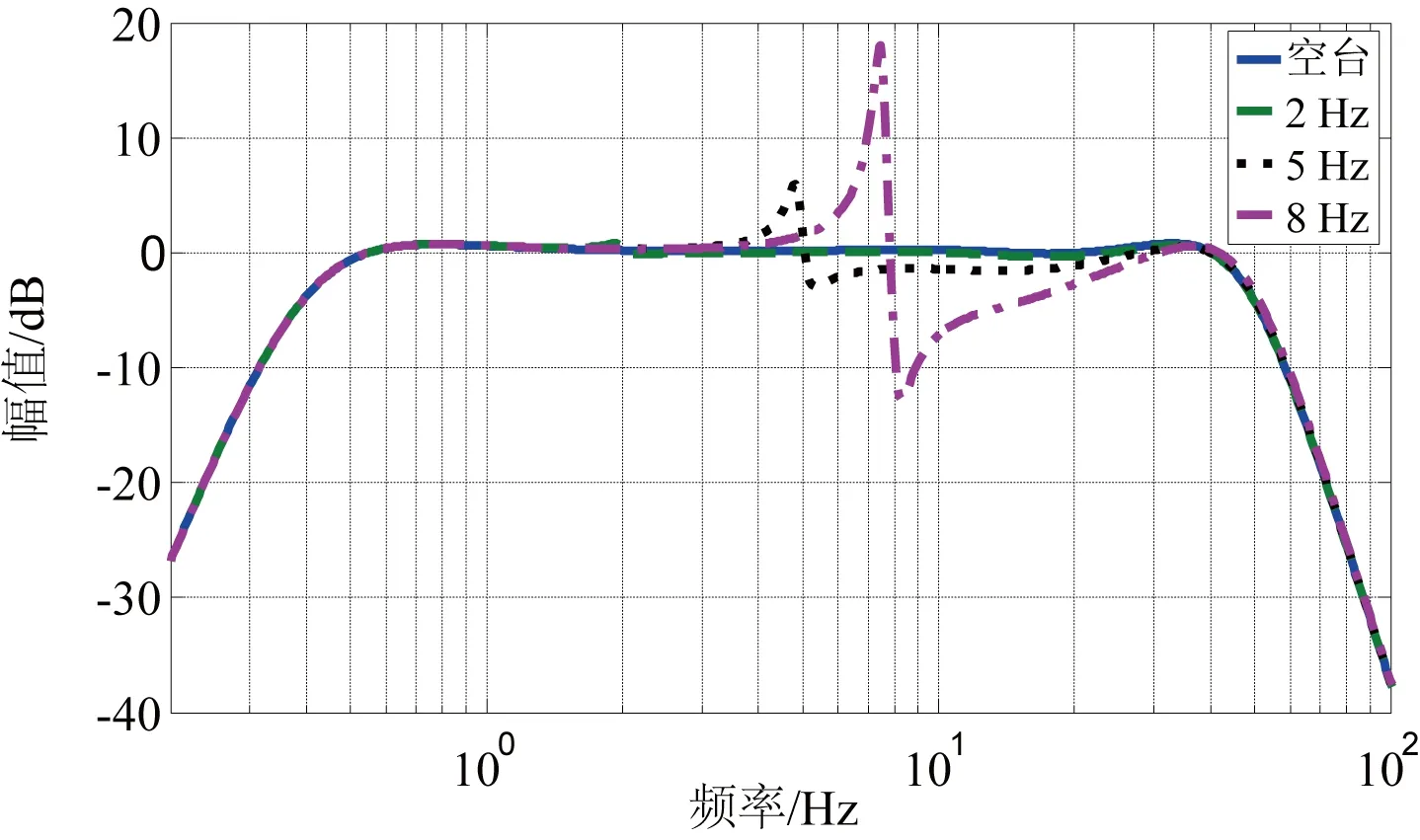
图11 不同频率单自由度负载振动台频率特性Fig. 11 Frequency Response of shaking table with different frequency SDOF payload
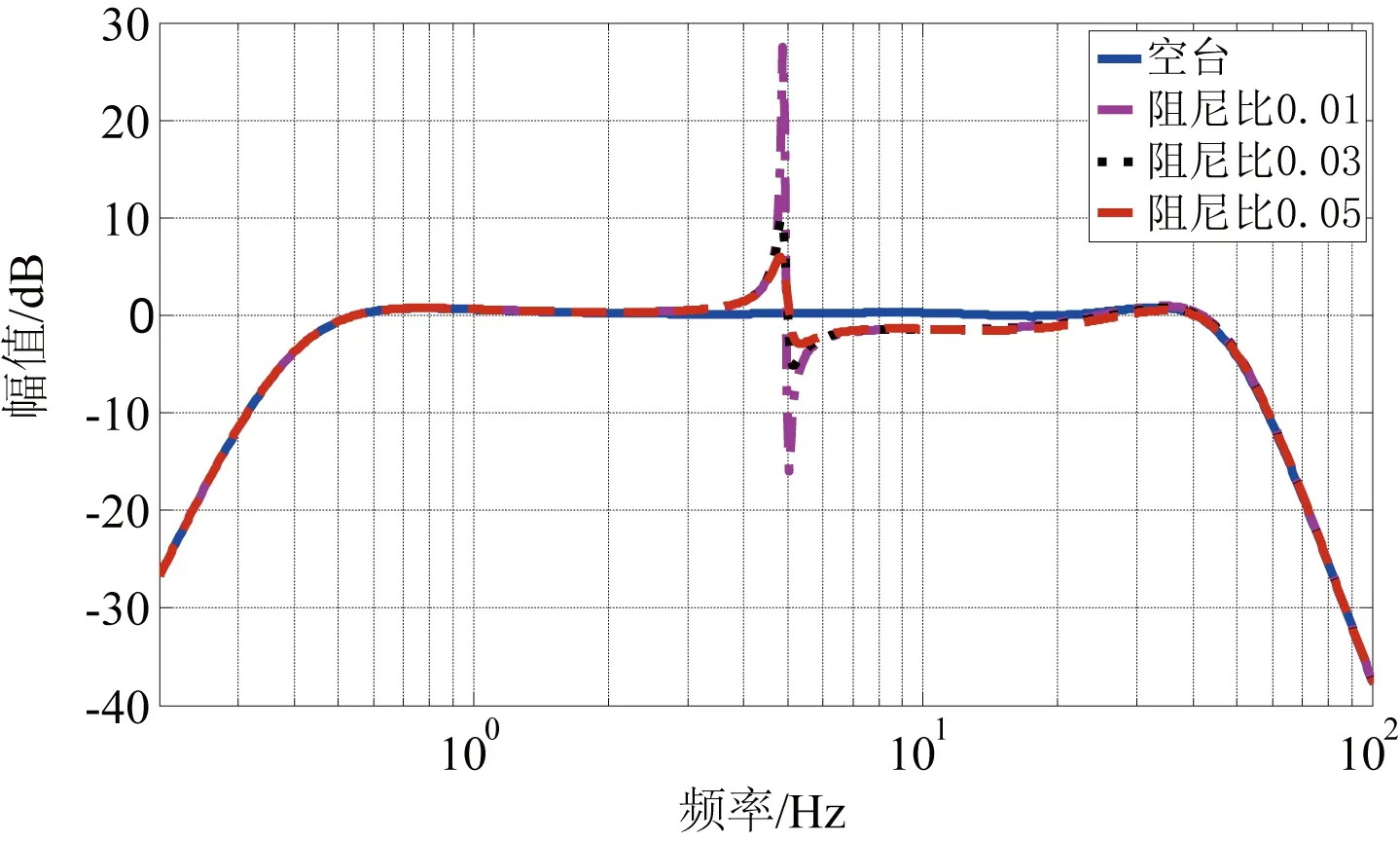
图12 不同阻尼比单自由度负载振动台频率特性Fig. 12 Frequency response of shaking table with different damping ratio SDOF payload
从图10中可以看出,系统在5 Hz(负载频率)左右出现了尖峰,小于5 Hz时被放大,大于5 Hz时被缩小,缩小的幅度远大于放大的幅度,且随着负载质量的增加对系统特性的影响越大。
从图11可以看出:随着负载频率的增加,对系统特性的影响越大,当负载频率小于2 Hz时,负载对系统的影响可以忽略不计。当负载频率较高时,在负载频率周围出现了不同程度的峰值,小于负载频率系统特性被放大,大于负载频率时被缩小,负载频率越大,对系统特性影响越大。
从图12可以看出:随着阻尼比的增加,对系统特性的影响减小,在负载频率周围处,阻尼比的影响较为敏感,负载频带以外几乎没有影响。
3 三参量控制下多自由度负载台面与试件共同作用分析
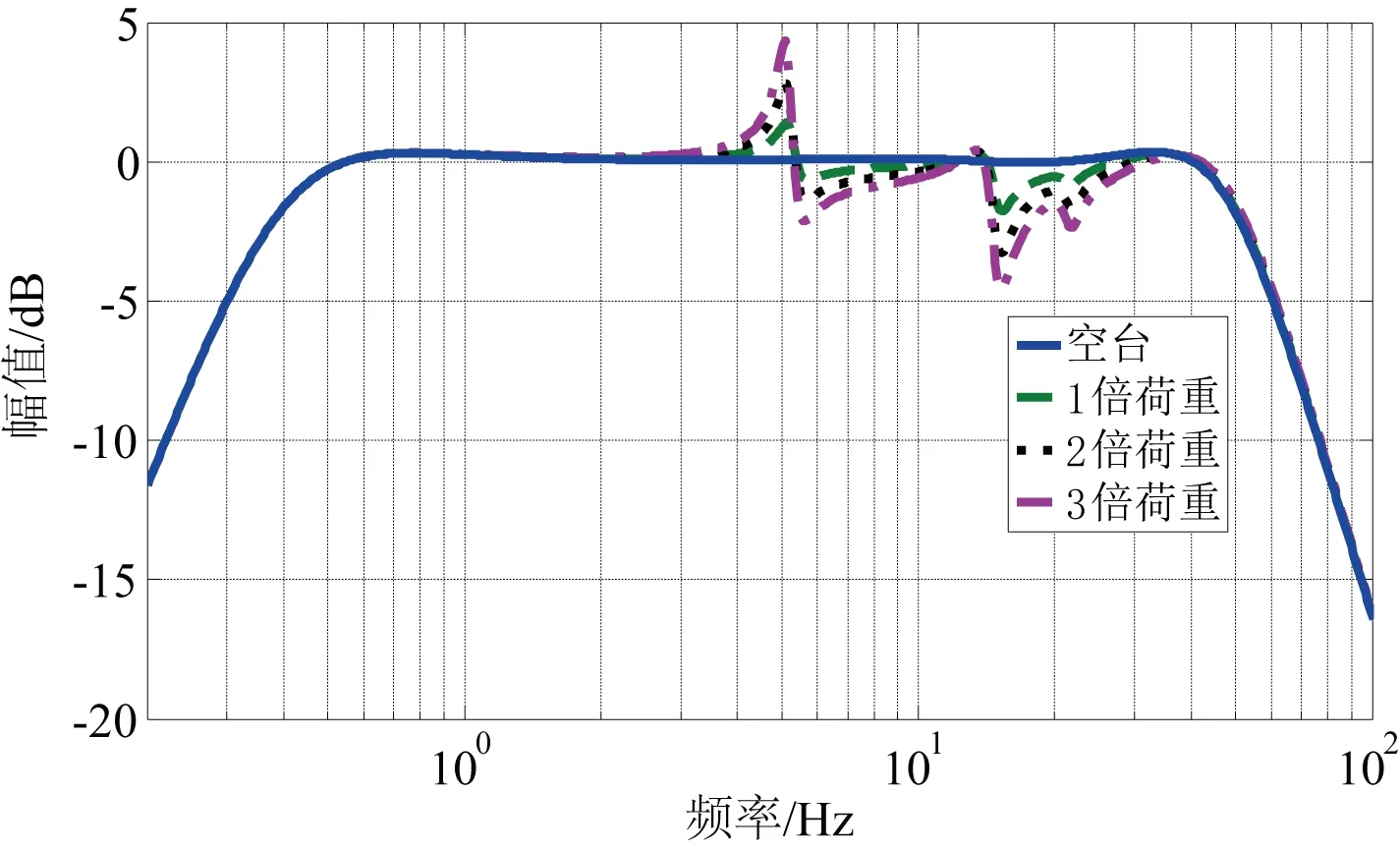
图13 不同质量多自由度负载振动台频率特性Fig. 13 Frequency response of shaking table with different mass MDOF payload
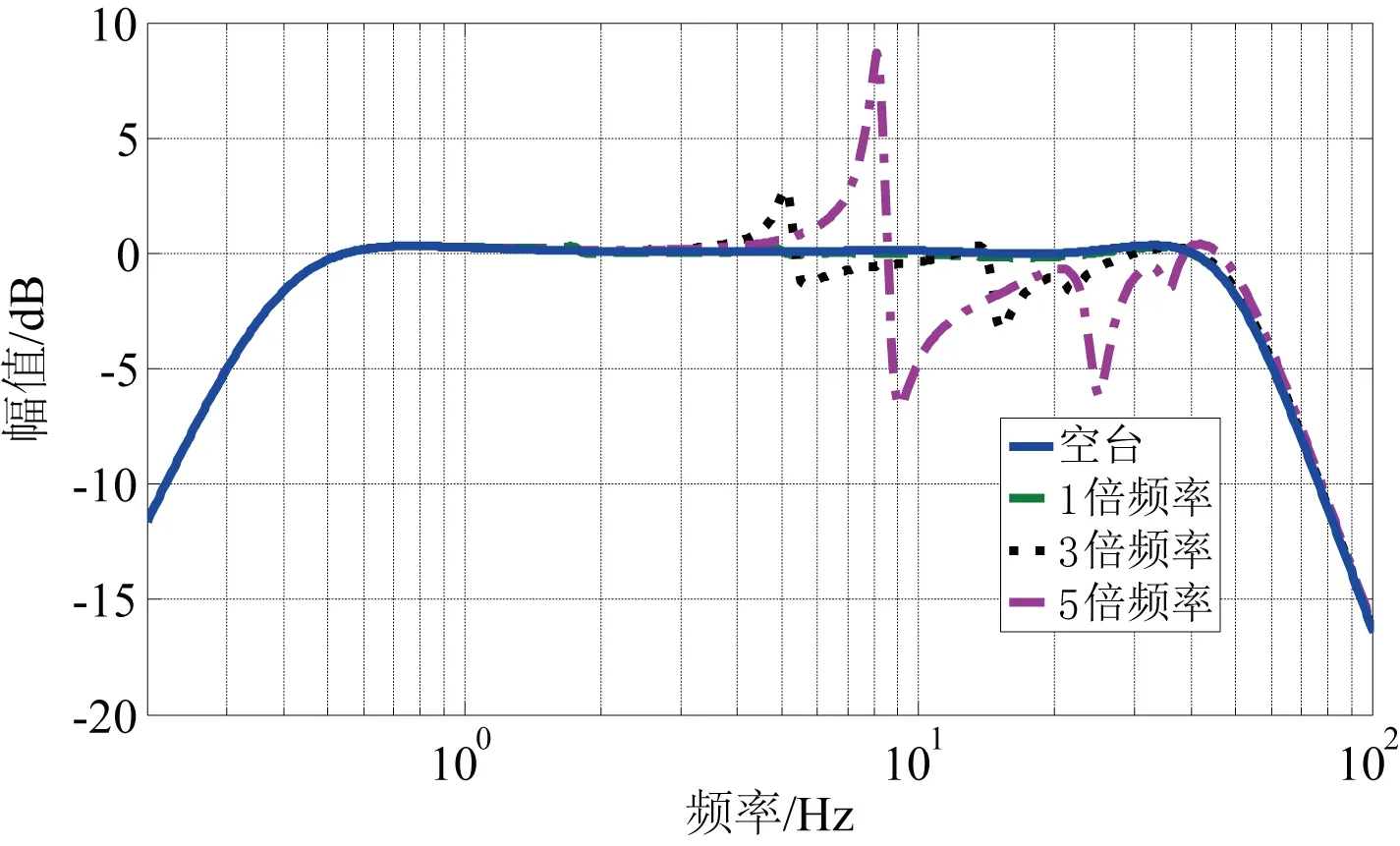
图14 不同频率多自由度负载振动台频率特性Fig. 14 Frequency response of shaking table with different frequency MDOF payload
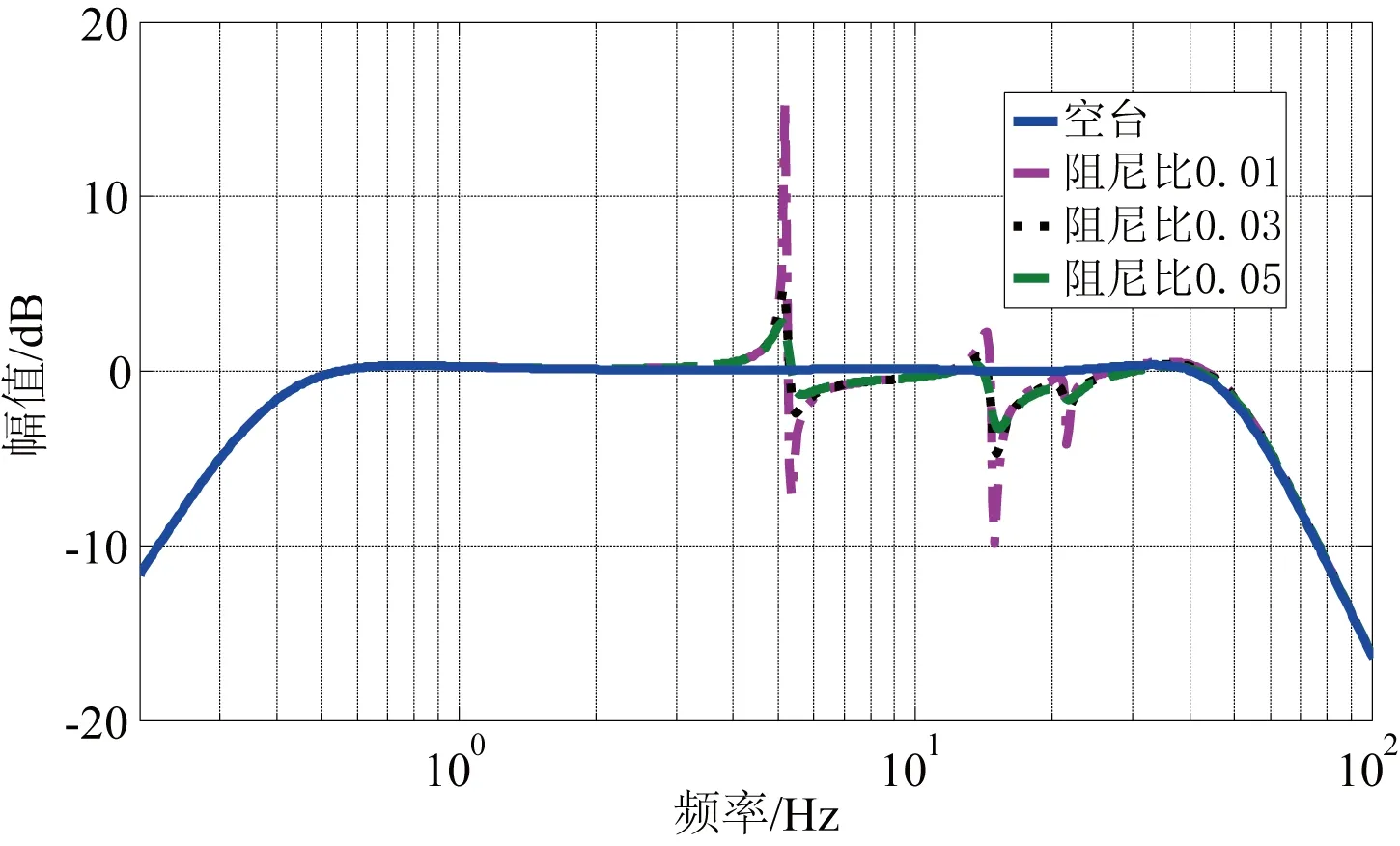
图15 不同阻尼比多自由度负载振动台频率特性Fig. 15 Frequency response of shaking table with different damping ratio MDOF payload
从图13可以看出:多自由负载对系统频响特性的影响与单自由度的相似,随着负载质量的增加,对系统特性的影响越大,每阶负载频率的周围处均出现峰值。
从图14可以看出:随着负载频率的增加,负载频率对系统特性的影响越大,当负载频率较低时,对系统特性的影响可以忽略不计,一阶频率对系统特性的影响最大。
从图15可以看出:随着阻尼比的增加,阻尼比对系统特性的影响越小,相比较负载质量和负载频率而言,阻尼比的影响频带较小,但是在负载频率处影响较为剧烈。
以上分析可知:无论是负载质量、负载频率和负载阻尼在各阶频率处均出现峰值,并且均以第一阶影响为主,与单自由度负载比较而言,各阶频率有相互补偿的趋势。
4 压差反馈补偿
以上分析可看出,试件对地震模拟振动台系统性能影响的关键是由于试件与台面间的反力作用,也就说,只要将试件与台面间的作用力消除,该影响就不存在了。为消除试件与台面相互作用对地震模拟振动台系统性能的影响,本文以地震模拟振动台台面为研究对象,提出一种压差反馈补偿控制算法,补偿流程如图16所示。试验中采用压差传感器测出作动器的出力,采用加速度传感器测出台面的加速度,试件与台面间的相互作用力F可以表示为式(9)所示:
F=AppL-Ma,
(9)
其中:M为试件的质量;a为试件的绝对加速度。
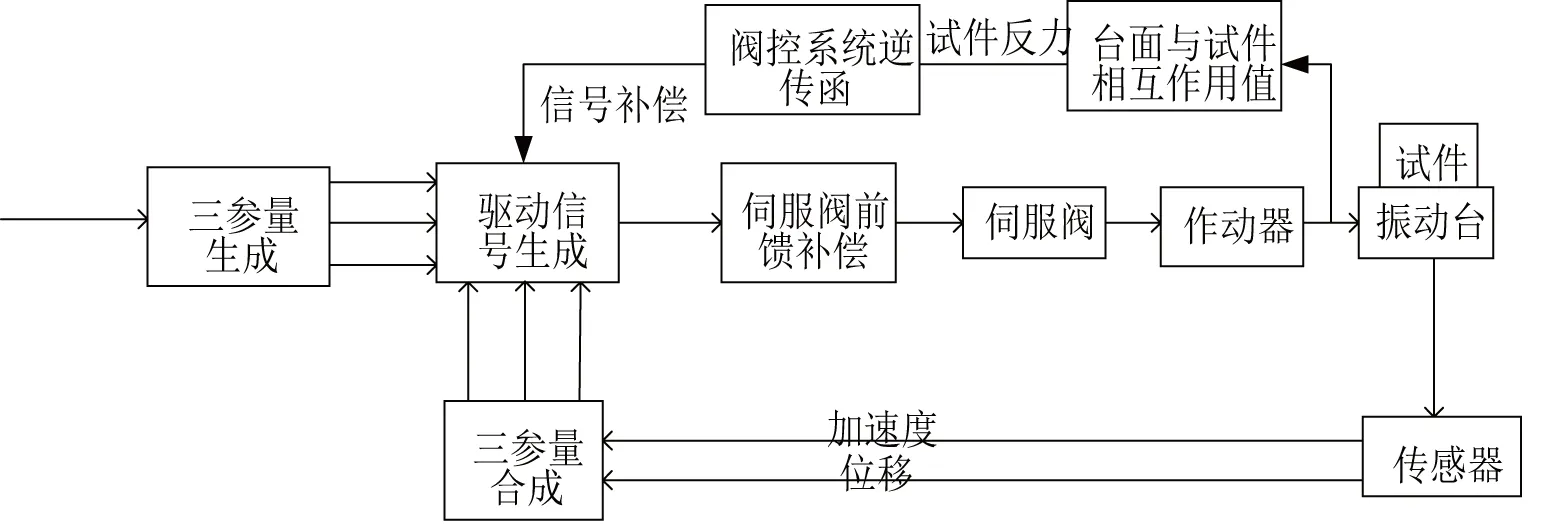
图16 试验试件压差反馈补偿Fig. 16 Differential pressure feedback compensation
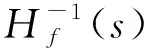
(10)
补偿信号可以表示为:
(11)
负载质量为1倍台面质量,阻尼比为0.05的单自由度负载压差反馈前后地震模拟振动台频响特性如图17所示。
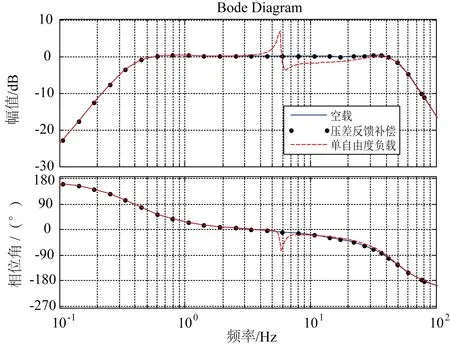
图17 压差反馈补偿下单自由度负载系统频响特性Fig. 17 Frequency response characteristic curve of system with differential pressure feedback compensation
从图17中可以看出:压差补偿后的地震模拟振动台与空载时地震模拟振动台特性完全一致,很好地补偿了试件与台面相互作用的反力。
5 结论
通过对地震模拟振动台建模、分析试件质量、阻尼及频率等对系统性能的影响,得出主要结论如下:
(1)无论是单自由度还是多自由度负载,试件质量、频率及阻尼均在一阶频率处均出现峰值,并以第一阶频率影响为主。
(2)与单自由度负载情况相比,多自由度负载在各阶频率处出现了不同程度的相互补偿趋势。
(3)采用压差补偿算法补偿后,地震模拟振动台系统的波形再现精度大大提高。
