基于分立求解的电气耦合综合能源系统多能流联合计算方法

徐 晶，徐 科，王世举，李 娟，张雪菲

（1.国网天津市电力公司经济技术研究院，天津 300171；2.国网天津市电力公司，天津 300010）

随着经济社会发展和生态环境的恶化，可持续发展理念深入人心。天然气发电机组NGU（natu⁃ral gas-fired generating unit）具有污染排放少，响应速度快和发电效率高等优点，被广泛应用于电力系统[1]，推动了电力系统与天然气系统之间的深度耦合，构成了典型的电气耦合综合能源系统IEGS（in⁃tegrated electricity-gas system）。然而IEGS在提高能源利用效率，实现可再生能源充分消纳的同时，也带来了系统安全运行的风险。一方面，天然气系统的故障将传导至电力系统，并引发停电事故。例如：2017年台湾地区发生的8.15大停电事故，其原因为天然气供应中断引起6台机组脱网，导致多轮停电，影响人口600多万[2]；2015年美国南加州Al⁃iso Canyon天然气泄漏引起燃气电厂天然气供应不足，严重影响了当地电力系统的正常运行[3]。另一方面，电力系统的不利影响也会危及天然气系统的安全运行。例如，随着美国可再生能源渗透率的提高，作为主要调峰资源的燃气电厂频繁动作，直接导致燃气管网压力的大幅度波动，威胁输气安全[4-5]。由此可见，随着电力系统与天然气系统之间的耦合日益紧密，二者间的交互影响所引起的安全问题必需高度重视，实现IEGS整体的安全分析具有重要意义，而电气耦合的多能流联合计算是这一分析过程的最基本环节。

针对IEGS的多能流计算已有部分学者进行研究。文献[6-8]利用能源集线器模型对NGU进行描述，并进一步对电力-天然气系统的耦合关系进行分析；文献[9-10]在电力系统潮流计算的基础上，提出一种IEGS多能流计算方法，为IEGS安全分析奠定了基础；文献[11-12]提出基于统一潮流雅克比矩阵的IEGS多能流计算方法。然而，目前的研究往往忽略天然气管网的运行特性和运行约束，以及电气耦合环节的一些细节，仅从宏观角度分析电气与天然气系统之间的互动联系，计算结果往往存在一定误差。由于将电气系统联立增加了大量高维非线性方程和决策变量，使统一求解法变得更加复杂。考虑到天然气系统及电力系统各自潮流计算较为成熟，本文提出了基于分立求解的IEGS多能流计算方法。这一方法通过能源耦合部分的能量等值将多能流待求信息分配到不同能源各自的求解模块，进行分立求解，物理意义明确。仿真结果表明，该方法可有效计算IEGS的运行状态，为系统安全性分析提供技术支撑。

1 IEGS多能流模型

IEGS多能流模型包括天然气系统模型、电力系统模型和天然气发电机模型。

天然气系统变量为节点天然气注入量和节点压力。天然气系统中的节点分为两种类型，一种是天然气注入量已知的节点，另一种是压力已知的节点。假定天然气气源为平衡节点，平衡节点的压力已知，天然气注入量未知；天然气负荷节点的天然气注入量已知，节点气压未知。

天然气管道分为带压缩机管道和不带压缩机管道，为简化起见，本文暂时不考虑带压缩机的管道[13]。对于不带压缩机的管道，天然气节点m到天然气节点n的管道流量fmn可表示为

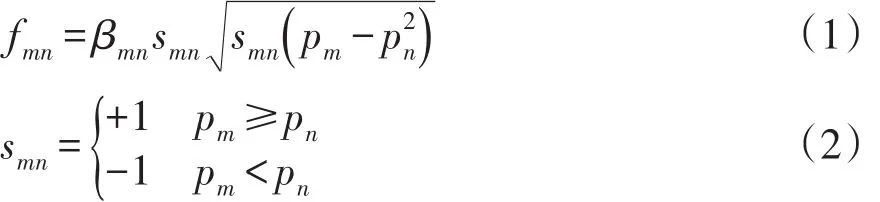
式中：βmn为管道阻力系数，与管道的粗糙度、直径和长度有关；pm为天然气节点m的气压；pn为天然气节点n的气压；smn为符号指示函数。

对天然气系统的任意节点，流入和流出的流量必须保持平衡，即

式中：为天然气节点m的注入流量；M为与天然气节点n之间有管道连接的天然气节点m的集合；Ls,m为天然气节点m的天然气供应量；Ll,m为天然气节点m的天然气需求量。

电力系统模型描述可以表示为

式中：J为与节点i有电气连接的节点j的集合；、分别为电力系统节点i的注入有功功率、无功功率；Pg,i、Qg,i分别为电力系统节点i上发电机的有功功率、无功功率；Pl,i、Ql,i分别为电力系统节点i上负荷的有功功率、无功功率；Vi、Vj分别为电力系统节点i、j的电压；Gij、Bij分别为导纳Yij的实部、虚部；θij为节点i、j之间的相角差。

设ΩNGU为IEGS中所有NGU集合，可表示为

式中，GUi为第i个天然气发电机，其中i=1，2，…，N，N为天然气发电机的总数。

系统中NGU有功注入向量W可表示为

式中，PU,i为第i个天然气发电机的有功功率注入。

天然气发电机通过消耗天然气进行发电，其天然气消耗与发电量的关系可表示为

式中：ai、bi和ci分别为第i个天然气发电机的消耗系数；LU,i为第i个NGU的天然气消耗量。

定义xeg和yeg为IEGS的状态变量和注入变量。IEGS的多能流模型由式（1）～（11）组成，可归纳为

式中：V、θ和p分别为电力系统节点电压、相角和天然气系统节点气压；Psp、Qsp和Lsp分别为电力系统节点有功功率注入、无功功率注入和天然气系统节点注入流量；xeg由电力系统节点电压、相角和天然气系统节点气压组成；yeg由电力系统节点有功功率注入、无功功率注入和天然气系统节点注入流量组成。

2 燃气及电力网络潮流计算模型

2.1 天然气系统潮流求解方法

根据基尔霍夫第一定律，天然气系统中任何一个节点注入流量的代数和为零。在天然气系统中，任何一个节点的净负荷（负荷需求减去天然气供应）等于流入该节点的全部流量减去流出该节点的全部流量，即式（3）～（4）用矩阵的形式可表示为

式中：L为天然气管网中的燃气负荷矢量；A1为降阶节点-支路关联矩阵；f为支路流量矢量。

图1为一个简单的天然气系统流量关系图，以图1所示的天然气系统为例，根据基尔霍夫第一定律由式（15）可得

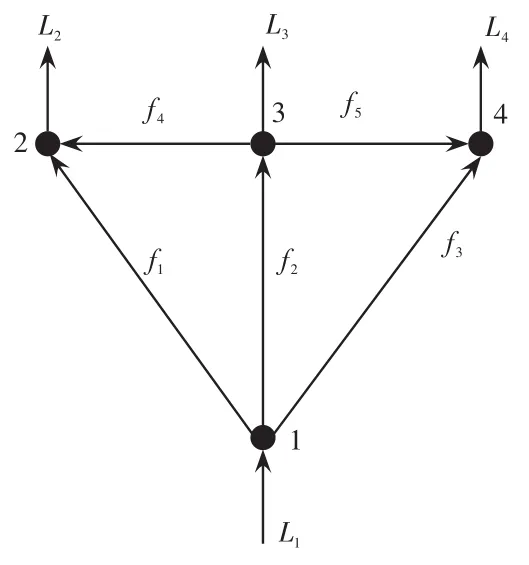
图1 一个简单的天然气系统Fig.1 A simple natural gas system

对矩阵A1中各元素符号进行规定，若支路气流流进该节点，则为正；若支路气流流出该节点，则为负。支路两端的压力平方差用矩阵形式可表示为

式中：ΔΠ为天然气管网中的压力平方差；Π为节点压力平方向量；A为全节点-支路关联矩阵；Πm为天然气节点m的气压平方。

根据图1所示的天然气系统，将式（17）表示为

根据式（17）、（18），将式（1）和式（2）改写为

式中：fi为第i条管道的流量；βi为第i条管道的管道阻力系数；si为符号指示函数；ΔΠi为第i条管道两端气压平方差。

在计算天然气系统潮流时，以气压的平方作为未知数，则式（20）可表示为

将式（22）代入式（15）可得

通过牛顿节点法可求解式（23），得到天然气网络节点气压分布，再通过式（22）计算出天然气流量分布。在这一过程中，首先要给出各节点压力的初始估计值，然后通过连续修正估计值，直到获得最终结果。设Fgas()为天然气节点误差函数，也就是所有节点压力平方的函数，除了参考节点外，整组误差可以表示为

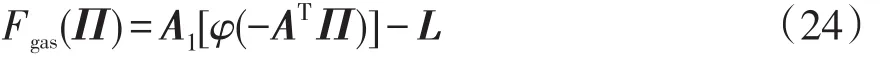
当压力平方值接近其真值时，天然气节点误差函数将会趋近于零，牛顿节点法就是求解公式组成的方程组，直到误差小于给定阈值。用于修正节点压力平方估计值的迭代过程可表示为

式中：Π(k)为第k次迭代中的节点压力平方；(δΠ)(k)为第k次迭代中的节点压力增量。

δΠ的计算过程可表示为

式中，Jgas为节点雅可比矩阵，可表示为

相比于电力系统的电压相角设置，天然气系统变量的初始化需要注意初始天然气气压的设置，否则会因为潮流发散而导致潮流计算失败。本文天然气节点压力设置是按照以气源节点为参考节点，按顺序将以后每个节点的压力减少2%进行初始化。

综上，天然气系统潮流求解过程如下：

步骤1根据天然气网络拓扑形成A及降阶节点-支路A1，读取cmn，计算天然气系统各个节点的净负荷，初始化节点压力；

步骤2以节点压力平方为变量，代入式（24）求解天然气节点误差函数；

步骤3根据式（25）计算新的节点压力平方，判断式（24）最大值是否小于阈值。若小于，得到节点压力平方真值，进入步骤4，否则进入步骤2；

步骤4由式（22）计算得到天然气流量分布。

2.2 电力系统潮流求解方法

通过Newton-Raphson法计算电力系统潮流的步骤如下：

步骤1读取电网拓扑及参数，形成节点导纳矩阵；

步骤2初始化电力系统状态变量V(0)，θ(0)；

步骤3计算电力系统节点误差函数Fe(V,θ)，即

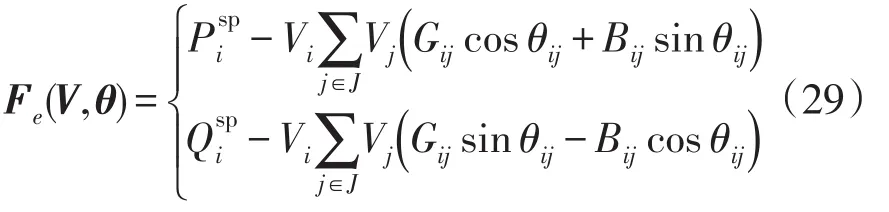
步骤4计算电力系统节点雅可比矩阵Je，即

步骤5计算迭代修正量ΔV和Δθ，即

步骤6更新电力系统状态变量，判断电力系统节点误差函数最大值是否小于阈值，即

若式（32）成立，迭代到此结束，进一步计算各线路潮流和平衡节点功率，反之进入步骤3。

3 基于分立求解的IEGS多能流计算方法

IEGS联合潮流计算本质上是高维非线性代数方程组的求解问题，通常在给定电/气网络拓扑、元件参数和源、荷参量等运行条件下，求解系统中的状态变量。为了便于说明，对系统中的节点进行分类，对于电力系统，节点可分为PQ节点、PV节点和平衡节点，求解是电压相角赋值；天然气可分为气源和气负荷，已知网络拓扑、气源压力及负荷燃气需求，求取网络流量气压分布。IEGS的节点分类及对应的已知量和待求量如表1所示。

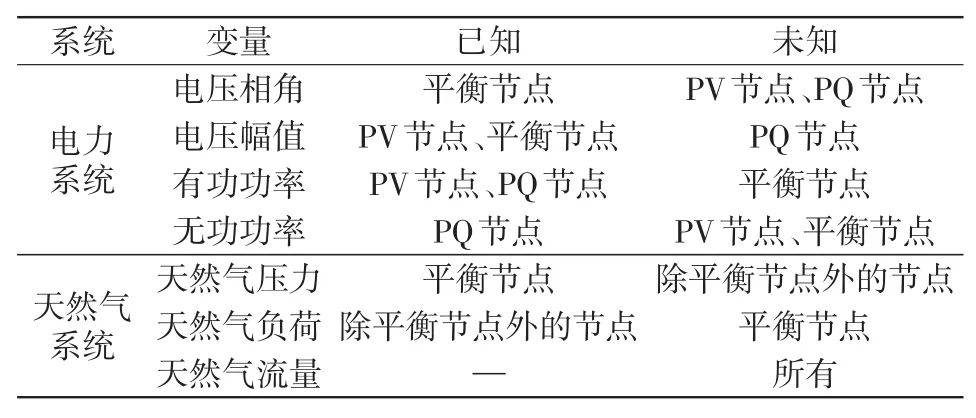
表1 IEGS节点分类Tab.1 Classification of nodes in IEGS

由于不同能源系统方程的联立增加了大量高维非线性方程与决策变量，使统一求解法变得复杂。考虑到天然气系统及电力系统各自潮流计算均较为成熟，本文采用基于分立求解算法的IEGS多能流计算方法。分立求解法通过能源耦合部分的能量等值将多能流待求信息分配到不同能源各自的求解模块，来进行分立求解，使物理意义明确，程序编写简便。

本文的电、气两系统的耦合环节为NGU。NGU在电力系统中往往作为PV节点处理，其有功功率已知，同时NGU在天然气系统中作为负荷，可根据其输出的有功功率由式（11）计算消耗的天然气。此时天然气发电机在电力系统中等效为一个有功出力已知的发电机，在天然气系统中等效为一个燃气需求已知的天然气负荷，从而实现天然气系统和电力系统的解耦。解耦后，分别运用电力系统潮流计算及天然气系统潮流计算，所得各类状态变量即为多能流仿真的最终结果，具体流程如图2所示。

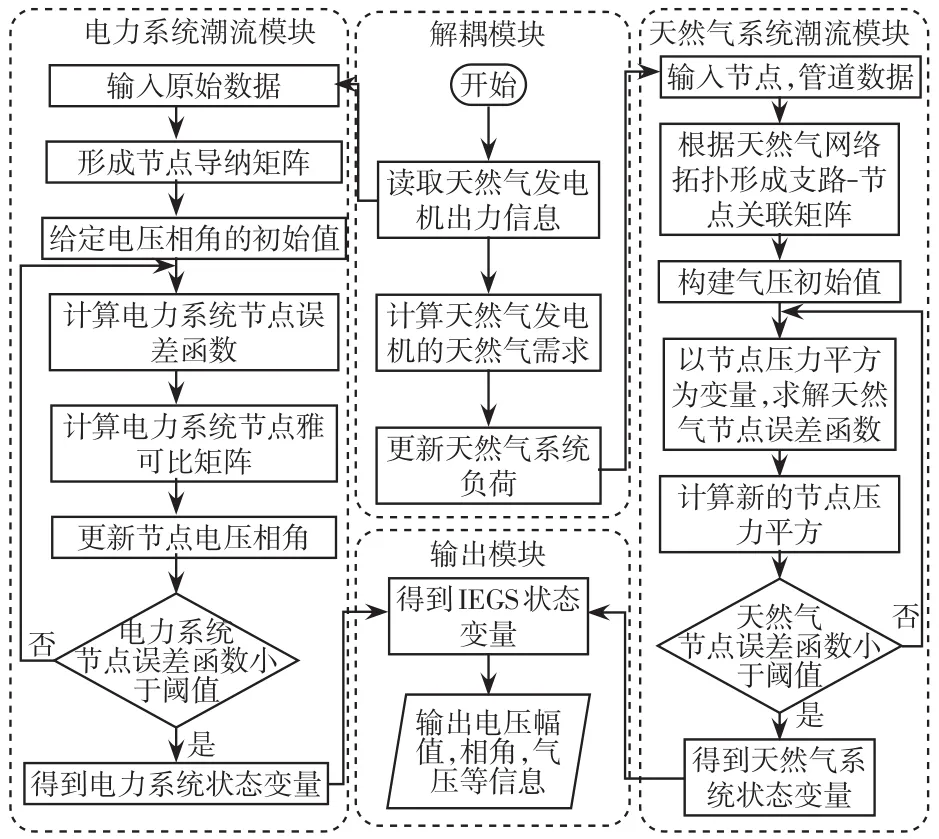
图2 IEGS分立求解算法流程Fig.2 Flow chart of discrete solution algorithm for IEGS

（1）解耦模块是将天然气系统潮流计算和电力系统潮流计算模块进行解耦。首先，读取天然气发电机的有功出力信息；然后，由式（11）计算其天然气消耗；最后，更新天然气系统负荷，即与天然气发电机相连接的天然气负荷节点，其天然气需求等于本地天然气需求加上天然气发电机的燃气需求。

（2）电力系统潮流模块是通过Newton-Raphson法计算电力系统潮流分布。首先，输入节点和支路的相关信息，形成节点导纳矩阵；接着，给定电压相角的初始值；然后，依次计算电力系统雅克比矩阵，更新节点电压相角值，不断迭代直到电力系统节点误差函数小于给定阈值；最后，得到电力系统的状态变量。

（3）天然气系统潮流模块是通过牛顿节点法计算天然气系统潮流分布。首先，根据节点和管道数据，形成支路-节点关联矩阵；接着，给定气压的初始值；然后，以节点压力平方为变量，依次计算天然气系统雅克比矩阵，更新节点气压平方，不断迭代直到天然气系统节点误差函数小于给定阈值；最后，得到天然气系统的状态变量。

（4）输出模块是用于输出分立求解算法中IEGS的状态变量。主要包括电力系统中所有母线节点的电压幅值和相角，以及线路的功率分布、功率损耗；天然气系统中各个节点的气压幅值，管道的流量分布。

4 算例分析

4.1 仿真模型

以典型的IEGS为例，验证基于分立求解算法的IEGS多能流联合计算方法的有效性。算例由WSCC9节点电力系统和修改的6节点燃气网络通过2个天然气发电机耦合而成[14]，EBi和GBi分别表示电网节点和燃气节点，其拓扑结构如图3所示。对于WSCC系统，EB1为平衡节点，EB2和EB3为天然气发电机G2和G3所在的节点，均为PV节点。G2和G3连接天然气系统的GB6和GB3，2个天然气发电机参数相同。天然气发电机消耗系数如表2所示，天然气网络参数如表3所示。

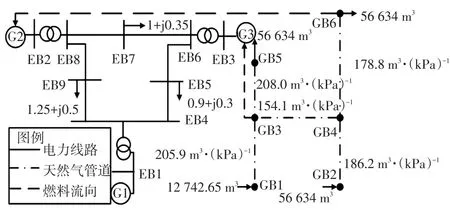
图3 IEGS的算例Fig.3 Numerical example of IEGS

表2 天然气发电机的消耗系数Tab.2 Parameters of natural gas generator

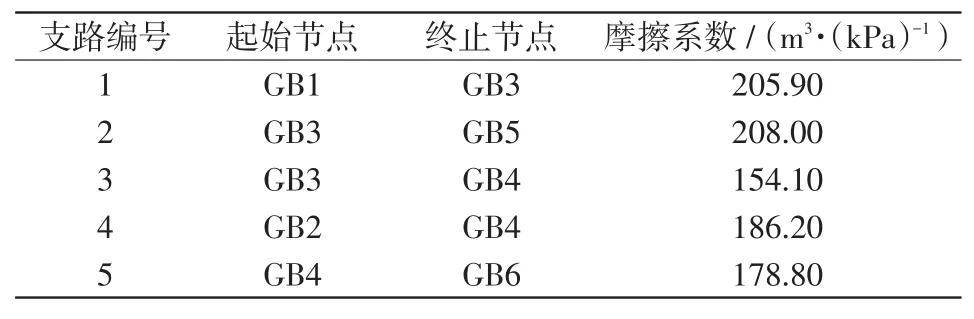
表3 天然气网络参数Tab.3 Parameters of natural gas network

根据NGU有功出力计算其天然气消耗，如表4所示。

表4 NGU的有功出力以及天然气消耗Tab.4 Active power output and natural gas consumption of NGU

考虑NGU的燃气需求，更新天然气网络的负荷如表5所示。

表5 天然气网络的负荷Tab.5 Load of natural gas network（including NGU gas demand） （m3·h-1）

将多能流待求信息分配到不同能源的各自求解模块。通过分立潮流计算，分别运行电力系统潮流计算及天然气系统潮流计算程序，获得天然气网络的气压分布及电网的节点电压相角等关键信息，即表1中的未知量。

由本算例得到天然气网络气压分布如表6所示，天然气网络流量分布如表7所示；电力系统节点电压相角如表8所示。在表8中，发电机有功注入为正，负荷有功注入为负；发电机无功注入为正，负荷无功注入为负；联络节点无功率注入

表6 算例1中天然气网络的气压分布Tab.6 Pressure distribution in natural gas network in Case 1 kPa

表7 天然气网络的流量分布Tab.7 Flow distribution in natural gas network （m3·h-1）

表8 电力网络的节点电压相角Tab.8 Node voltage phase angle of power network

4.2 结果验证

对多能流计算结果进行验证，针对表6所给出的天然气气压分布情况，验证表7所列出的天然气流量分布是否正确；验证所有节点是否满足基尔霍夫定律，即流入与流出节点的流量相同。

（1）讨论流量分布计算结果是否准确。以1号管道为例，该管道的起始节点GB1的气压为3100.5kPa，终止节点GB3的气压为2 822.14 kPa，管道的摩擦系数为205.90 m3/kPa，代入式（1）可得

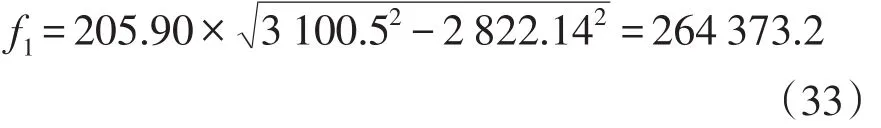
1号管道的流量与表7中所列的流量值计算结果一致。对于剩余的4个管道，分别代入气压值计算，并与表7中所列的流量值进行比对，可以发现，本文所列的流量计算结果与气压分布状态对应无误。

（2）验证在表7所示的流量分布状态下，流入流出节点的流量是否守恒。以GB1为例，作为IEGS的气源节点，在不考虑天然气泄漏损耗的状态下，流入该节点的天然气流量应该为网络中所有节点的需求和。由表5数据可算得，GB2～GB6的天然气需求和为264 379.98 m3/h。流出该节点的天然气流量即为1号管道的流量，由表7可知，两者是一致的。以此类推，表7所示的流量分布状态符合表5所列的天然气系统负荷信息，符合基尔霍夫定律，由此得出天然气潮流计算结果的正确性。对于电力系统的潮流分布的校验与上述原理相同且已非常成熟，这里不再赘述。经验证，电力系统潮流计算结果也是正确的。

5 结语

本文基于分立求解思想，提出了一种面向IEGS的多能流联合计算方法。首先，从“源-网-荷”全环节出发，对IEGS供能单元、网络环节及用能单元中的关键单元建模；然后，以天然气系统、电力系统的网络传输模型为基础，构建IEGS的多能流模型，该模型在NGU环节将两系统解耦，将待求量分配到不同系统独立求解，并加以协同；最后，通过两个典型算例验证了本文方法的可行性和准确性。仿真结果表明，本文方法物理意义清晰，多能流计算结果准确，可以很好地反映系统的运行状态，能够为IEGS的规划、运行及评估提供技术支撑。