含规模化充电桩的微电网运行优化方法

2022-01-27于会群蔡国顺时珊珊彭道刚

电力系统及其自动化学报 2022年1期

于会群，蔡国顺，时珊珊，张浩，彭道刚，尹申

（1.上海电力大学自动化工程学院，上海 200090；2.国网上海市电力公司电力科学研究院，上海 200437；3.同济大学电子与信息工程学院，上海 200090）

由于国家大力提倡利用清洁能源发电，使分布式能源发电的装机容量占比越来越大，有效利用分布式能源对促进节能减排，实现能源可持续发展具有重要作用。随着车网互动V2G（vehicle-to-grid）技术在电动汽车EV（electric vehicle）行业的快速发展，如何利用区域内装设大规模双向充电桩，实现车网双向互动，让规模化电动汽车EVs（electric ve⁃hicles）参与微电网的经济优化管理[1]，使微电网的调控手段更加丰富灵活，安全应急响应能力更强，已成为当今研究的热点之一。

目前，已有的文献关于EV参与微电网优化管理的研究均集中在经济分析和降低负荷峰谷差等方面。文献[1-2]利用EV分布的时空特征，构建EV有序充放电的负荷模型和实时电价响应模型，并将EV与其他分布式发电单元参与微电网的经济调度；文献[3]为使研究微电网中EV换电站与微电网所属不同的决策机构效益达到最优，构建了微电网经济调度双层优化模型；文献[4]为解决大规模EVs接入配电网引起负荷峰值增加的难题，提出一种含大规模EVs接入的配电网多目标优化调度方法，该方法以优化EV充电来降低系统负荷峰谷差。然而，上述文献构建的经济调度模型只是单独考虑微电网经济性、用户利益和微电网运行的安全性这3个要素，而未把微电网运行管理的安全性、经济性和EV用户参与意愿进行统筹考虑。

对于多目标优化问题的求解方法主要分为3类：①基于数学方法，例如，采用混合整数线性规划MILP（mixed integer linear programming）、混合整数非线性规划MINLP（mixed integer nonlinear program⁃ming）[5]方法。但由于优化调度问题的维数不断增加，导致这些方法的计算量巨大。②改进的粒子群优化PSO（particle swarm optimization）算法，例如，采用PSO算法与差分进化DE（differential evolution）算法相结合[6]，随机漂移粒子群优化RDPSO（random drift particle swarm optimization）算法和帝国主义竞争算法 ICA（imperialist competition algorithm）结合[7]、变异、交叉[8]，以及选择3种不同算子与PSO算法相结合[9]等方法。但这些方法在寻找全局最优解的能力和陷入局部最优的可能性等方面存在不足，特别是在高维、高约束的问题中，限制了它们的应用。

基于以上分析，本文从微电网运营商的管理角度出发，综合考虑微电网运行的安全性、环境治理和用户参与这3个因素，建立大规模EVs参与由光伏PV（photovoltaic）、风机WT（wind turbine）、微燃机MT（micro-turbine）、储能系统 BESS（battery energy storage system）组成的微电网运行管理优化模型，该模型以实现微电网的运行管理费用、环境污染治理费用及负荷波动方差最低为目标。针对这一模型为非线性、非凸多目标问题，提出以多智能体系统和混沌粒子群优化CPSO（chaos particle swarm opti⁃mization）算法相结合的多智能体混沌粒子群优化MACPSO（multi-agent chaotic particle swarm optimi⁃zation）算法，并对模型进行求解。最后以某个园区的微电网为例，分析不同响应度对公共大电网、区域内可控发电单元出力方面的影响。

1 构建规模化EVs响应调度模型

1.1 EV的行驶特性

大规模EVs主要考虑的是私家车，受用户使用习惯的影响，其需求功率具有时空不确定性，需分析EV用户的旅行链及行驶特性，而EV的行驶特性涉及的因素比较多，本文从以下3个方面进行设定。

（1）用户日行驶里程。根据美国家庭出行旅行统计数据[10]，拟合出用户日行驶里程d近似符合对数正态分布，即d～log,N(μd,σd2)。其中，μd为日行驶里程的平均值；σd为其对应的标准差。设定d～log,N(10.45,3.262)。

（2）开始充电时间。假设EV车主在行驶结束后开始接入区域微电网充电，车主的最后一次返程时间t0服从正态分布[2，4]，即t0～N(μt,σ2t)，设定t0～N(12.73,4.722)。

（3）充电电量。根据日行驶里程d和单位能耗的线性关系，可得动力电池荷电状态的概率密度分布函数表达式[11]为

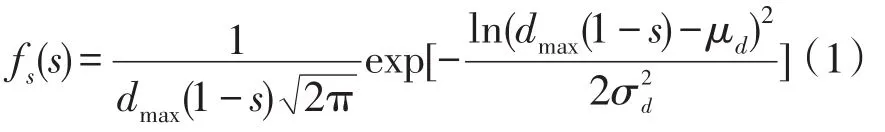
式中，s为EV动力电池荷电状态SOC（state of charge）的随机变量，设定s～N(14.23,8.432)。

1.2 规模化EVs的调度模型

假定区域内的EVs有部分用户响应区域微电网管理中心的调度信息，向微电网充放电；而有部分用户不响应调度信息，随机接入进行无序充电，其调度结构框图如图1所示。根据区域内EVs的运行特性，将区域响应调度EVs集群划分为充电集群和放电集群，则t时刻EV用户充放电响应度可分别表示为

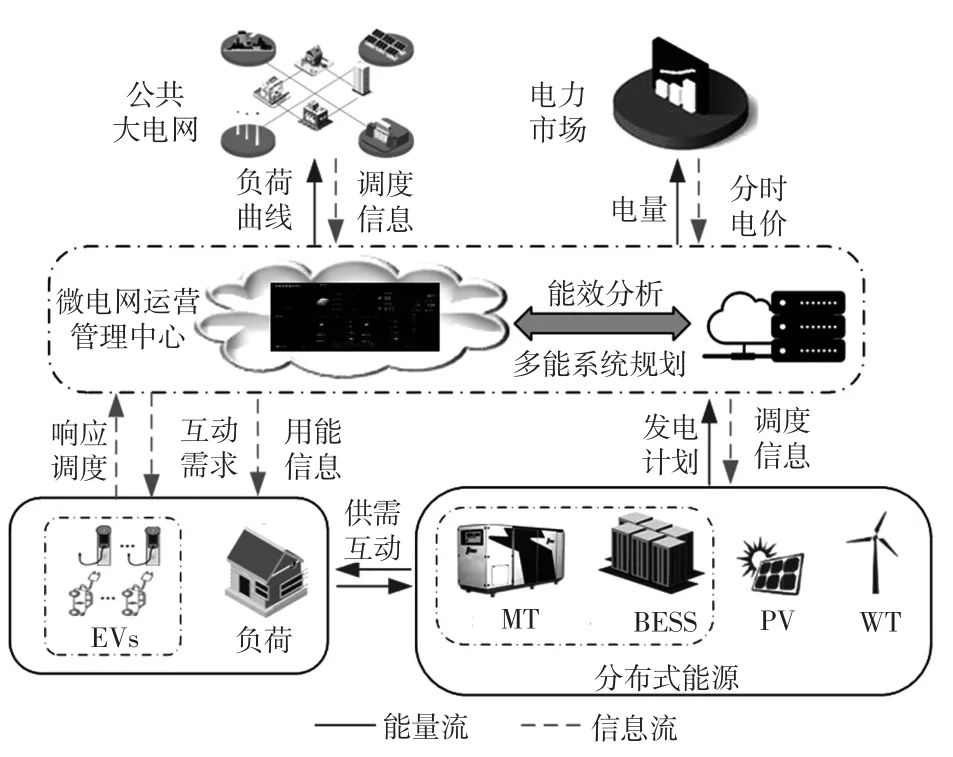
图1 规模化EVs响应区域微电网调度结构框图Fig.1 Block diagram of scheduling structure when largescale EVs respond to regional microgrid

式中：N为区域内的EVs总数；Ndis(t)为响应放电信息的EV数量；Nc(t)为响应充电的EV数量；φdis(t)为EV用户放电响应度；φc(t)为EV用户充电响应度；φ(t)为EV用户响应度。当EV用户响应充电时φdis(t)=0；当EV用户响应放电时φc(t)=0。

1）EV的无序充电模型

受区域内按装的充电桩功率的限制，假设EV的充电功率等于所连接充电桩的功率，不同类型的充电桩其充电功率不一致，可得EV的充电持续时长[2]，即

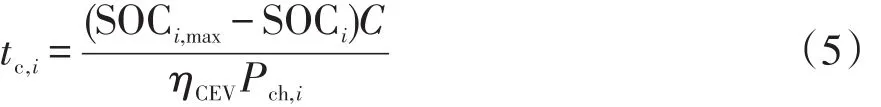
式中：SOCi,max、SOCi分别为第i辆EV的最大荷电状态和开始充电时的荷电状态；Pch,i为第i辆EV所连接充电桩的功率；C为第i辆EV的动力电池容量；ηCEV为第i辆EV的充电效率。

t时段区域内总无序充电负荷可表示为

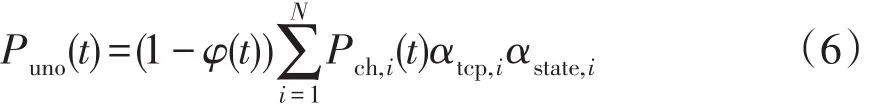
式中：Puno(t)为t时刻区域内总无序充电负荷，t=1，2，…，24；Pch,i(t)为t时刻连接充电桩的充电功率；αstate,i为充电桩的状态，αstate,i=1表示充电状态；αtcp,i表示当停车时间tp,i大于需要充电持续时间tc,i时，开始计算充电功率，此时αtcp,i=1。

2）用户响应调度的充放电模型

EV用户响应调度的充放电，即用户响应区域微电网管理中心的调度信息，有序接入区域微电网中进行可控充放电。假设第i辆EV用户在响应调度信息时，也将动力电池的荷电状态SOCi、停车时间tp,i、下一次的行程及EV单位耗电量等重要参数反馈给区域微电网管理中心，管理中心根据反馈的参数信息计算用户其余行程的必要荷电状态SOCrest,i，综合用户焦虑的荷电状态SOCanx,i，以及为保护电池预留不低于20%的容量裕度，计算EV的充放电时间，充电持续时间可由式（5）计算，放电持续时间[12]可表示为

式中：ηdEV为EV的放电效率；Pdis,i为所连接充电桩的放电功率。

根据所连接充电桩的放电功率，可得t时刻区域内EVs总充放电功率PresEV(t)，即

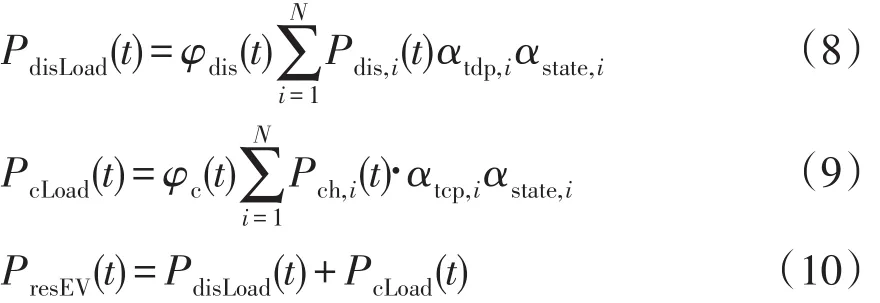
式中：PdisLoad(t)为t时段区域内EVs的放电功率；PcLoad(t)为t时段区域内EVs的充电功率；αtdp,i表示当停车时间tp,i大于持续放电时间td,i时，开始计算放电功率，此时αtdp,i=1。

2 EVs参与区域微电网运行管理优化模型

2.1 目标函数

在满足区域微电网安全运行条件和用户出行需求的前提下，合理优化可控分布式能源、公共大电网输入功率、可响应调度EV接入数量等可控变量，并在整个调度周期内使区域微电网运行管理费用、环境污染治理费用及负荷波动方差达到最低水平。

1）含规模化EVs的微电网运行管理费用

含规模化EVs的微电网综合运行管理费用主要包括微电网的经济运行成本和响应调度的EVs参与调度的激励费用，其计算表达式为

式中：T为一个调度周期；NDG为区域内装设的发电单元种类；Cn( )PDG(n,t)为第n类分布式发电单元的发电成本；CW,n( )PDG(n,t)为第n类发电单元的维护费用；PDG(n,t)为第n类发电单元的发电功率；cgrid(t)、Pgrid(t)分别为t时刻微电网管理中心和电网公司协议分时电价和微电网向大电网购电功率；Cexcit(t)为激励EVs参与调度费用；Cdc(t)为运营管理中心从用户购电（EV放电）和向EVs售电（EV充电）的差额而需支付额外费用。

第n类分布式发电单元的发电成本可表示为[13]

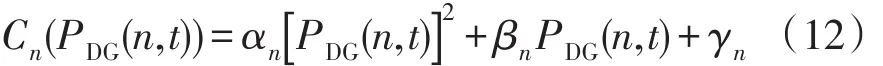
式中：αn、βn、γn为成本常数，与分布式发电单元的类型有关。

发电单元的维护费用与发电单元发电功率近似成比例[4]，即

式中，为第n类分布式发电单元的维护系数，不同种类的分布式发电单元的维护系数不同，不同种类的维护系数可参考文献[14]。

区域微电网管理中心为使用EV动力电池的可用容量，向车主采取一定的激励措施，以吸引EV车主积极响应区域微电网管理中心的调度信息，向区域微电网充/放电。采取激励措施所需的费用可表示为

式中：ρexcit(t)为t时刻单位激励费用，其值本文以参考分布式发电度电补贴标准0.37元计算；Λi(t)为t时刻充电桩的连接状态，Λi(t)=1为充电桩处于连接状态，Λi(t)=0为充电桩处于未连接状态。

用户充放电时段电价差异而增加的额外费用可表示为

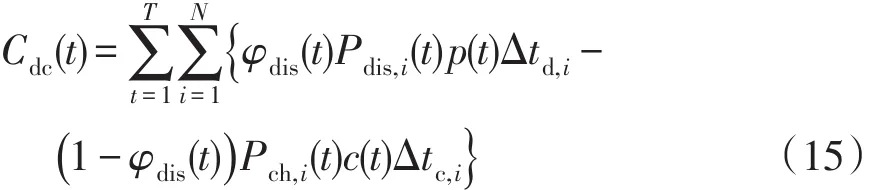
式中：p(t)为用户t时刻向区域微电网放电的上网售价；c(t)为用户在t时段的充电电价；Δtc,i、Δtd,i分别为第i辆EV用户向区域微电网持续充、放电时间。

2）微电网运行污染物治理费用

微电网运行污染物治理费用F2可表示为

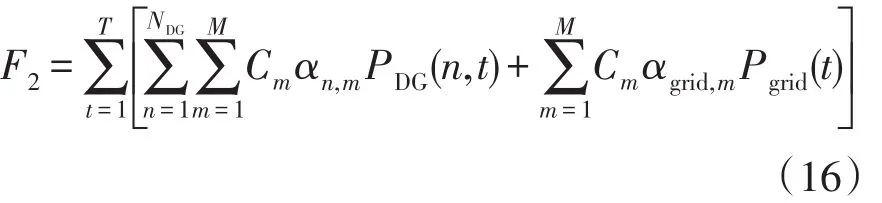
式中：M为污染物种类，发电过程主要考虑NOx、SO2和碳排放3种；Cm为处理这m类污染物的每千克费用；αn,m为第n类发电单元所产生第m类气体污染物的排放系数；PDG(n,t)为第n类发电单元的发电功率；αgrid,m为公共大电网传输电能时所产生m类气体污染物的排放系数；Pgrid(t)为区域微电网和公共大电网间双向流动的功率，大电网向区域微电网供电为正，区域微电网向大电网供电为负。

3）区域微电网的负荷波动方差

规模化EVs接入区域微电网，需要考虑区域内的EVs充放电负荷对整个区域微电网的影响。因此，降低负荷波动方差也是供电侧管理的一个重要目标[15]，通过提高区域微电网的安全稳定性，以促进区域微电网的经济运行。区域微电网的负荷波动方差F3可表示为

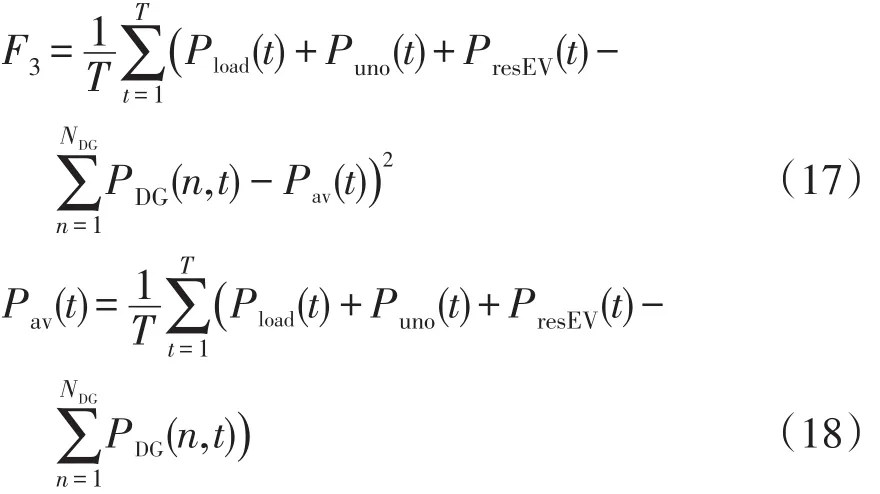
式中：Pload(t)为t时段区域微电网内的基本用电负荷；Puno(t)为t时段区域内EVs无序充电负荷；PresEV(t)为t时段区域内EVs响应充放电负荷。

综上，区域微电网的运行管理费用和污染物治理费用可以统称区域微电网的综合运营管理费用，将两者合并为同一个目标函数，与负荷波动方差构成多目标函数，通过线性加权法转化为目标函数F为

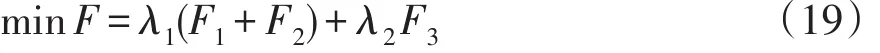
式中，λ1、λ2为权重因子，其中λ1+λ2=1。

通过对各目标函数赋予权重系数，将多目标模型加权为综合单目标模型，为克服主观经验进行赋权可能存在误差，本文应用熵权法进行赋权，形成加权单目标优化模型，具体步骤[16]如下。

步骤1分别以目标函数Fl(l=1,2,3)作为优化目标，求解所得模型的优化结果。为以目标函数Fl进行单目标求解时目标函数Fj的函数值，j=1,2,3。

步骤2根据步骤（1）可得单目标函数值和综合目标函数值。

步骤3根据单目标函数值和综合目标函数，对目标函数值进行一致化和无量纲化处理，得到预处理后的目标函数值集合。

步骤4应用熵权法求取目标函数权重系数。如果极大目标函数和极小目标函数的权重系数分别为和，可得加权综合目标函数，即

2.2 约束条件

1）等式约束条件

区域微电网内要实现供需侧的功率达到平衡状态，其功率平衡约束条件可表示为

式中：Pn(t)为区域内第n类发电单元的供电功率；Pbess(t)为BESS总充放电功率，Pbess(t)＞0为放电，Pbess(t)＜0 为充电。

区域微电网中不等式约束主要包括区域内的可控发电单元出力上下限约束、爬坡率约束、BESS容量约束等约束条件，具体约束条件可参考文献[4，14]。

2）双向充电桩充放电功率约束

式中：Pch,i,max、Pdis,i,max分别为所连接充电桩的充放电功率上限和下限；tstart,i、tend,i分别为开始充放电时间和结束充放电时间；Tφ为用户响应调度信息向区域微电网放电时段。

3）EV充放电状态约束

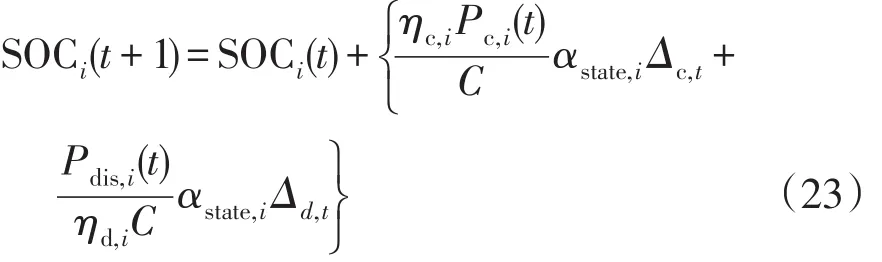
式中：SOCi(t+1)、SOCi(t)分别为第i辆EV动力电池在（t+1）、t时段的荷电状态；ηc,i、ηd,i分别为第i辆EV的充、放电效率；Δc,t、Δd,t分别为充、放电持续时间。

4）EV用户出行需求约束

为满足用户下一次出行需要，用户可以设定所期望动力电池的电量，即

式中：为SOCdesired,i为离开充电桩时用户所期望的动力电池荷电状态；SOCi(tleave)为EV离开充电桩时动力电池的实际荷电状态。

2.3 约束条件处理

区域内的各发电单元、规模化EVs以及用电负荷的需求与响应特性各异，各发电单元约束条件呈现非线性特性，如何在这些非线性等式约束的条件下，使区域微电网的运行管理费用、环境污染及负荷波动方差达到最佳状态，是目前研究的难点之一。本文采用文献[13]的利用惩罚函数方法来处理相关约束条件，该方法以增加一项惩罚项来生成新的目标函数，即

式中：F′(x)为新适应度函数；F(x)为原适应度函数；P(x)为惩罚函数。

EVs参与区域微电网的经济优化需要在满足多个约束条件下，使区域微电网的运行管理费用、环境污染治理费用及负荷波动方差达到最低，可将此经济优化问题转化为含多个不等式约束条件的最小化问题，即

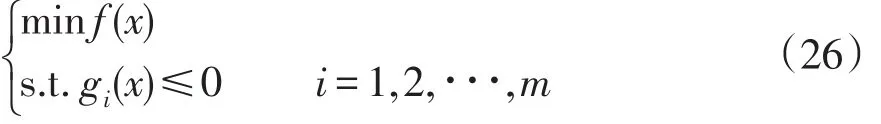
式中，gi(x)为约束条件的表达式。

辅助目标函数可定义为

式中，Pf为惩罚参数，本文参考文献[17]设置惩罚参数的范围为[0.01，100]。

2.4 模型求解算法

为提高算法对模型求解的速度及收敛精度，本文采用CPSO算法与多智能体系统相结合的MACP⁃SO算法。该算法充分利用PSO算法的群搜索特性和智能体的智能搜索特性，加强算法内部信息的多样化和传递性[18]，完善群内部信息反馈结构，同时利用混沌局部搜索策略以提高粒子的智能性和全局搜索能力[19]。

1）智能体的行动策略

则可控发电单元智能体在解空间中的位置将保留下来，否则可控发电单元智能体的位置会根据区域内用电负荷变化而发生变化，可控发电单元进行位置更新[19]为

式中：d=1,2,···,D，D为所求解问题的维度；r为[0，1]之间的随机数。

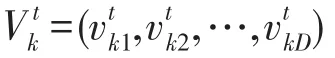
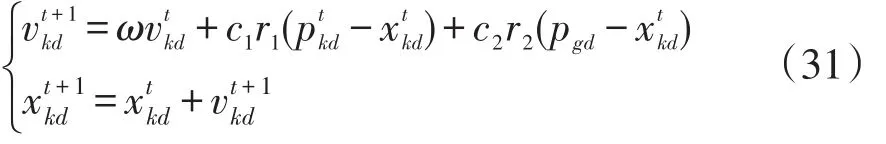
式中：k=1,2,···,Popmax，Popmax为粒子群总数；r1、r2为[0，1]之间的随机数；c1、c2为学习因子；ω为惯性权重，本文采用文献[20]线性递减惯性权重策略来提高MACPSO算法的寻优性能。

2）混沌局部搜索策略

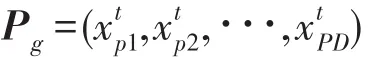
式中：为[0，1]之间的混沌变量；为向量Pg中的元素；为全局最优智能体在解空间中位置的最小、最大范围。

式中，为一个混沌变量可行解序列，根据经济优化模型的目标函数，分别计算出可行解序列中每个可行解向量的适应度值，并保留适应度值最小所对应的可行解向量，即可控单元的计划出力。

基于MACPSO算法的区域微电网经济优化流程如图2所示。

图2 基于MACPSO算法的区域微电网经济优化流程Fig.2 Flow chart of regional microgrid economic optimization based on MACPSO algorithm

3 算例分析

3.1 模型参数设置

本文以某个用电负荷为MW级的园区微电网为例进行相关实例仿真分析，园内装设充电桩可分为3个等级，各等级充电桩所允许充电功率如表1所示，园区中3个等级充电桩的比例为50%、30%和20%。由于园区微电网装机容量和传输功率的限制，假设该园区内有100辆EVs。本文选用该园区微电网中典型风光发电功率预测曲线如图3所示，园区内装设的发电单元参数、单位发电成本及维护费用、环境治理成本系数[22-23]、该地分时电价价格[23]分别见表2～4。假设园区内所有EVs为同一类型，充放电功率和充放电效率均相同，EV参数如表5所示。

表1 充电桩充电功率等级Tab.1 Charging power levels of charging piles

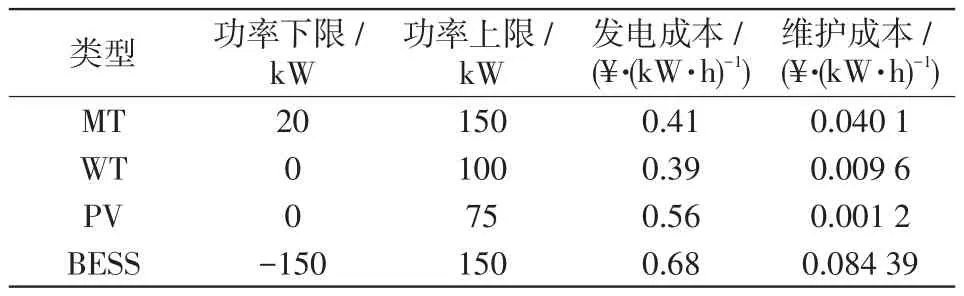
表2 各发电单元参数、单位发电成本及维护费用Tab.2 Parameters of each power generation unit，unit power generation cost and maintenance cost

表3 环境治理费用及污染物排放系数Tab.3 Environmental governance cost and pollutant emission coefficients

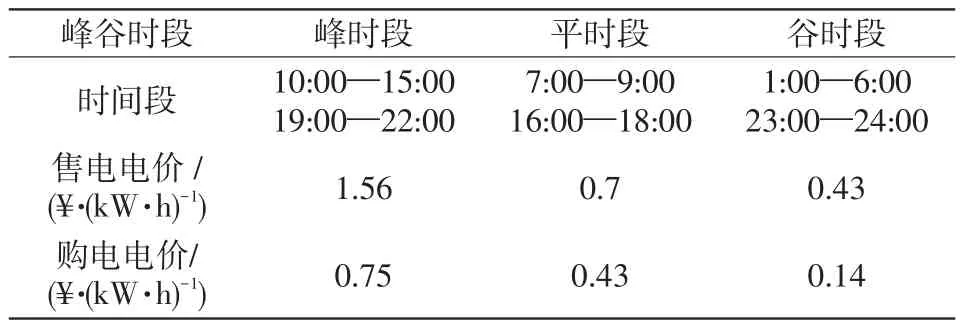
表4 当地分时售电价格Tab.4 Local time-of-use electricity prices

表5 电动汽车参数Tab.5 Parameters of electric vehicle

图3 区域内典型风光发电功率预测曲线Fig.3 Typical power generation prediction curves for wind and photovoltaic in one region

运用MACPSO算法对模型进行求解，设置优化算法相关参数，其中，种群规模Popmax=400，最大迭代次数Tmax=600；参考文献[13，20]设置惯性权重上限wmax=0.9，惯性权重下限wmin=0.4，设置初始自学习因子c1s=2.5，终止自学习因子c1f=0.5，初始社会学习因子c2s=0.5，终止社会学习因子c2f=2.5；参考文献[19]设置环境大小lsize=20，最优混沌环境的大小hsize=3，搜索半径r=0.5，最优混沌时的迭代次数hcir=10。

3.2 验证规模化EVs响应调度模型的有效性

为验证本文建立规模化EVs响应调度模型在降低负荷波动性方面的有效性，选取3种不同EV充放电模型：①用户自主充电模型；②基于峰谷分时电价有序充放电模型；③本文建立的响应调度模型。应用3种不同的充放电模型，计算区域内包含100辆EVs充放电负荷的总用电负荷，设定用户响应度为100%，其运行结果如图4所示。

图4 3种不同模型的区域微电网总负荷Fig.4 Total load of regional microgrid for three different models

由图4可以看出，基于峰谷分时电价的有序充放电模型，可以根据峰谷分时电价信息进行有序充放电，其负荷波动方差由用户自主充电模型的299.28降低到264.55，波动方差减少11.6%，但会造成大量EVs用户同时向微电网进行充放电产生新的用电“高峰”，对微电网产生新的冲击。而响应调度模型是根据峰谷分时电价和区域内负荷信息引导EV向微电网进行充放电，其负荷波动方差相较于用户自主充电模型、峰谷分时电价的有序充放电模型分别减少了25.3%、15.5%，可见，响应调度模型可以提高区域内负荷的平滑性。对比有序充电负荷曲线和响应调度负荷曲线可知，响应调度模型可以充分挖掘规模化EVs作为“移动储能装置”的潜力，增加微电网的备用容量。

3.3 不同权重系数对优化结果的影响

为分析不同权重系数对优化结果的影响，表6比较了5组不同的权重系数下的优化结果，其中，各组中权重系数λ1取值分别为0、0.3、0.5、0.8、1；权重系数λ2分别为1、0.7、0.5、0.2、0。并根据优化结果统计一个调度周期内微电网的综合运行管理费用及负荷波动方差，如表6所示。

由表6中不同权重系数的优化结果可以看出，设置不同的权重系数会对优化结果产生影响，当权重系数λ1增大时，微电网运行费用和环境污染费用逐渐降低，而负荷波动方差随权重系数λ2的减小而增大。为选择合适的权重系数使微电网的运行管理费用和环境污染治理费用，以及负荷波动方差等指标达到最佳运行状态，首先，求取在单目标下模型的优化结果，即选取表6中的数组1和数组5的运行结果数据，获得微电网运行管理费用、环境污染治理费用，以及负荷波动方差的最大值分别为为94 099.872¥、10 735.098 ¥、285.38，最小值分别为31 190.257¥、6 976.039¥、12.56；然后，应用熵权法计算各目标函数的权重系数，可得权重系数λ1、λ2分别为0.586、0.414；最后，应用所得权重系数加权不同目标函数，求解所提的模型，可得微电网运行管理费用、环境污染费用和负荷波动方差分别为31 984.413¥、7 694.969¥和120.236。

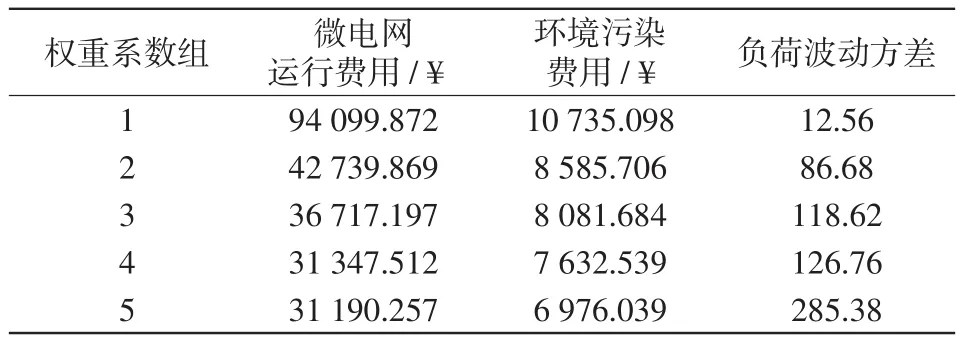
表6 不同权重系数的优化结果对比Tab.6 Comparison among optimization results with different weight coefficients

3.4 不同响应度的可控发电单元出力

研究不同响应度的可控发电单元出力情况，选取区域内用户响应度分别为0%、50%、80%、100%，其运行结果如图5所示，并统计1个调度周期内不同用户响应度的微电网的综合运行管理费用，以及负荷波动方差如表7所示。图5中，GRID为公共大电网的功率曲线。

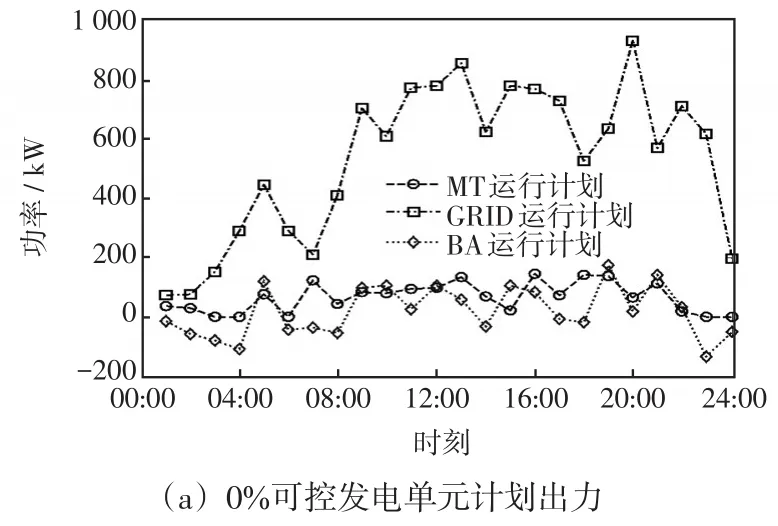
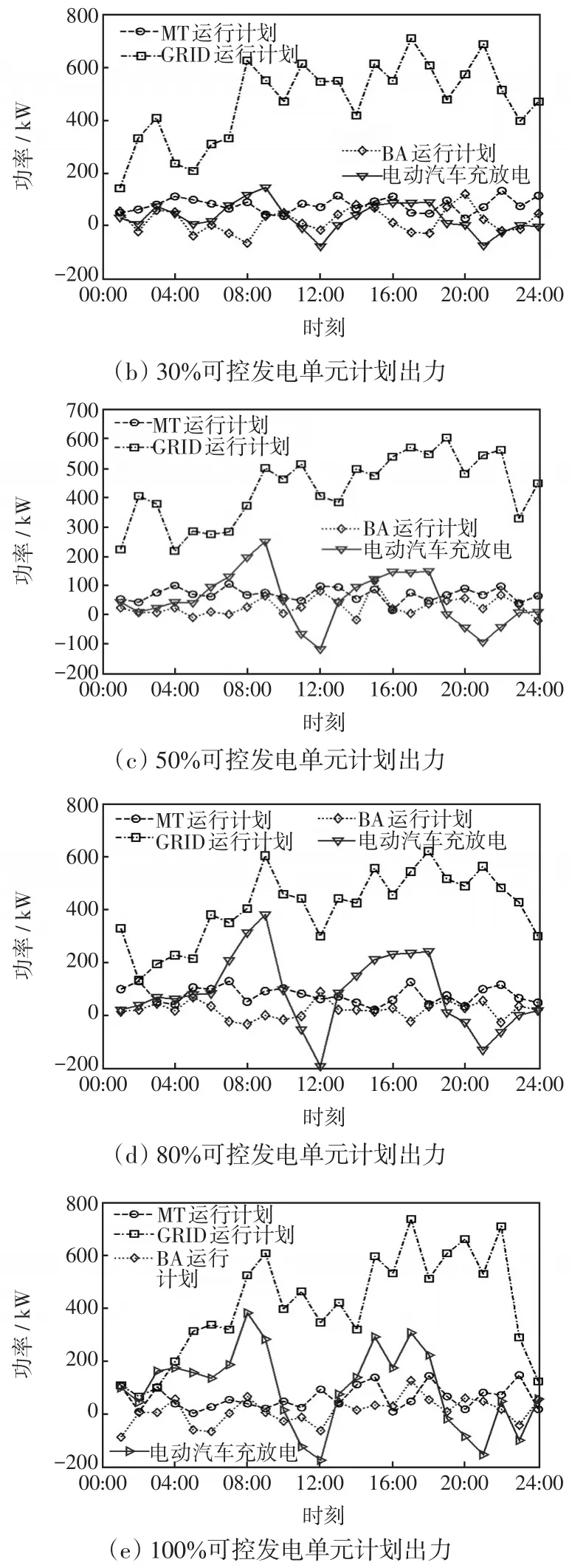
图5 不同用户响应度的可控发电单元计划出力Fig.5 Planned output from controllable power generation units with different user responsiveness

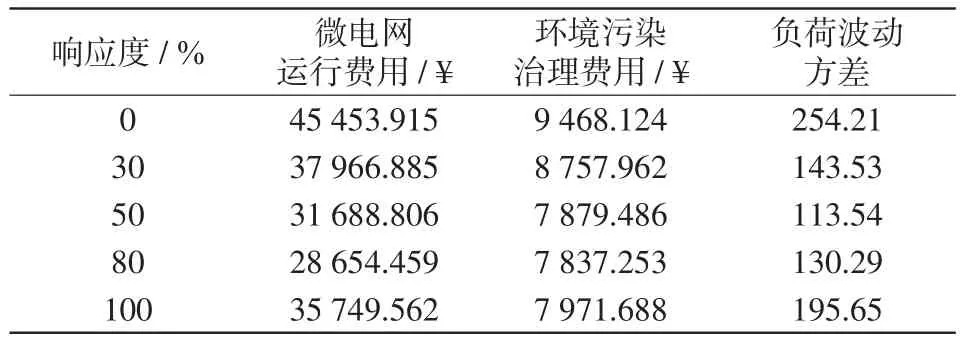
表7 不同用户响应度的微电网指标对比Tab.7 Comparison among microgrid indicators with different user responsiveness

由图5（a）中公共大电网供电功率变化曲线可知，在8：00—20：00时段规模化EVs无序接入微电网，微电网的用电负荷在用电高峰时段使用电需求急剧上升，导致公共大电网向微电网供电量也随之增加，易使公共大电网处于超负荷状态。对比图5及表7统计数据可知，当用户响应度在30%～80%时，随着用户响应度的增加，微电网的运行管理费用和环境污染治理费用都相应减少，负荷波动方差有先减小后增大的趋势。在用户响应度为100%时，大规模EVs接入区域微电网内进行充放电，由于区域微电网分布式能源装机容量的限制，使得区域内用电需求增加，导致微电网的相关费用也相应增加，同时，负荷波动方差相较于响应度为50%和80%的负荷波动方差有所增大。

3.5 不同优化算法的优化结果对比

为验证MACPSO算法在求解高维、非连续和多约束优化问题的有效性，分别采用MINLP数学方法、PSO算法、CPSO算法，以及基于多智能体系统竞争与合作机制的多智能体粒子群优化MAPSO（multi-agent particle swarm optimization）算法对本文建立的经济优化模型进行求解，将不同算法的寻优结果和MACPSO算法的求解结果进行对比分析。取种群规模为400，最大迭代次数为600，不同算法的收敛曲线如图6所示，优化结果对比如表8所示，设定用户响应度为80%。

图6 不同优化算法的收敛曲线Fig.6 Convergence curves of different optimization algorithms

表8 不同优化算法的优化结果对比Tab.8 Comparison among optimization results of different optimization algorithms

由图6可知，PSO算法的收敛速度最快，但算法容易出现早熟现象，不能收敛到全局极值点；MIN⁃LP方法的求解时间虽相对PSO算法求解过程所需时间相差不大，但其优化精度明显优于PSO算法；CPSO算法中通过增加混沌搜索策略在一定程度上提高算法的全局搜索能力，进而避免了陷入局部极值点，但其收敛精度还有待提高；MAPSO算法在求解过程方面需要较多的迭代次数和时间才能达到收敛，但在优化结果方面有较大改进；MACPSO算法与几种优化方法相比，虽然算法中融合多智能体系统及混沌搜索机制，使其在时间消耗方面有所增加，但其寻优效果最好。由表8数据分析表明，对本文建立的经济优化模型进行求解，其优化结果的运行费用、环境污染治理费用及负荷波动方差达到最小。可见，MACPSO算法在求解高维、非连续和多约束优化问题具有较好表现。