新能源接入配电网的电压无功自律-协同控制

宋明刚 ，陶 骏 ，张华赢 ，朱乾龙

（1.安徽大学电气工程与自动化学院，合肥 232000；2.安徽大学电能质量教育部工程中心，合肥 232000；3.南方电网公司新型智慧城市高品质供电联合实验室（深圳供电局有限公司），深圳 518020）

在面临能源转型和能源自主安全可控的双重压力下，加速能源清洁化转型显得尤为迫切。近3年，我国新能源投资约占世界的70%，截至2019年底，风电、光电装机分别增长至2.1×108kW和2.05×108kW，均居世界首位[1]。随着新能源渗透率的不断增加，给配电网乃至输电网的调度运行、电能质量和系统保护等带来一系列不容忽视的问题[2-4]。其中，由于新能源出力及用户侧负荷的波动，大大增加了配电网电压越限的可能，使电压稳定控制成为迫切需要解决的问题。在已有的研究中，主要通过分散式控制与集中式控制2种方法来降低分布式电源DG（dis⁃tributed generation）并网对配电网电压的影响[5-6]。

在集中式控制方面，文献[7-8]提出一种具备有限连续电压控制能力AVC（automatic voltage con⁃trol）的系统，该系统以综合经营成本最小为优化指标，并通过在电压幅值约束中考虑安全冗余的形式表征风电预测误差，最终给出系统电压/无功调度方案；文献[9]将传统无功补偿设备动作次数描述为调节代价，同时考虑网络损耗和电压稳定指标构造优化目标方程，并利用粒子群算法进行优化计算，最后仿真验证所提方法能够有效解决负荷波动情况下的配电网无功优化问题。在分散式控制方面，文献[10-11]阐述了配电网中DG主要分为逆变型DG和同步机型DG，相较于同步机型DG，逆变型DG因其本身有功、无功可控，且具备与有源电能质量治理装置相同的换流器拓扑，使逆变型DG在实现并网发电的同时具备无功补偿、有源滤波等电能质量问题治理的潜力，为DG介入地区电网动态无功优化调度奠定了基础；文献[12]针对DG大规模接入引起的系统电压问题提出一种无源解决方案，但该文献并未涉及DG与传统无功补偿装置的协调控制；文献[13]从直角坐标系下的无功电压灵敏度矩阵角度，验证了调节DG出力能够有效改善系统电压，但该方法仅考虑了电压稳定性指标，未能对实际运行中系统经济性、安全性进行综合考量，且改善电压质量时对DG的有功做出了改变，难以实现对新能源发电的充分利用。

为综合集中式与分散式控制的优点，文献[5]提出一种集中支撑分布式电压控制CSDVC（central⁃ized support distributed voltage control）方法，在利用ε-解耦法对所得灵敏度矩阵进行分区的基础上，计算得出负荷无功最优变化，进而得到控制后的参考值。但该文献并未对控制变量进行具体细化分析，且仅针对某一时间断面进行优化计算，默认系统为恒定负荷，与实际配电网运行状态差异较大。文献[14]提出了用于光伏大规模接入的配电网混合电压/无功控制方法，该方法由协调标准控制环与不协调瞬态云运动控制环组成，共同降低功率损耗及电压偏差。然而，该文献并没有充分利用DG本身的无功调节能力，且过于频繁的优化操作，在对电网产生冲击的同时还会引起对传统无功补偿设备疲劳寿命的影响。

针对负荷及DG出力波动下电压稳定控制和传统设备与DG协同优化研究的不足，本文依据“集中优化管理，分区自律控制”思想，提出考虑DG接入的配电网自律-协同控制方案。在该方案中，全局协同优化侧重于系统运行安全性与经济性，建立以有功网损、电压偏差、补偿设备调节成本为目标的配电网动态无功优化模型，采用基于综合赋权的快速粒子群算法优化计算，并以优化结果指导区内电压自律控制；分区自律控制侧重于系统电压稳定性，基于凝聚型系统聚类与全局协同优化结果，由各子区域内动态无功资源进行就地补偿，提高电压质量，实现“分区自治”。最后在改造后的IEEE 33节点系统上进行仿真验证，通过多场景对比证明了所提方案在充分挖掘DG本身无功调节能力的同时完成了与传统设备的协同优化，具备良好的电压稳定控制能力。

1 基于无功源控制空间的聚类分析

1.1 灵敏度指标的计算与中枢节点的确定

在配电网实际运行中，往往由于负荷及DG出力的波动性导致系统电压失稳，而网络中各节点功率-电压变化关系在雅可比矩阵中有着直观体现，各节点电压灵敏度可由雅可比矩阵求逆获得。针对一个n节点网络，假定节点1～m为PQ节点，m+1～n-1为PV节点，第n个节点为平衡节点，在极坐标下，其牛顿-拉夫逊潮流计算方程为

由于系统电压控制与稳定性分析在强调电压幅值变化影响的同时弱化电压相角变化影响，因此不考虑H和J项，且在中高压系统中，电压幅值与无功强耦合而与有功弱耦合，此时无功对电压波动起主导作用，因此本文仅考虑电压与无功的关联，即可满足一般工程精度的要求。

令有功注入维持不变，即ΔP=0，得

式中：ΔU、ΔQ分别为系统PQ节点的电压和无功变化列向量；S为系统电压/无功灵敏度矩阵，它反映系统的电压与无功变化之间的对应联系。

1.2 构建无功源控制空间

当负荷、DG出力大幅波动引起网络节点电压变化时，系统可采取调整有载变压器变比，合理设置无功补偿装置投切容量和改变发电机端电压等措施来抑制主导节点的电压波动。此时，发电机、无功补偿装置等无功源的控制能力与负荷节点电压等被控对象之间的关系尤为重要[15]，因此，本文根据该关系建立无功源控制空间。

设系统内无功源节点数为g，构成集合G；待分区的负荷节点数为l，构成集合L。其中，每个无功源视为该空间的一条坐标轴，建立一个g维无功源控制空间，在该空间中，每个负荷节点i均可使用一个g维矢量(xi1,xi2,…,xig)作为坐标来描述。定义负荷节点i在第j个无功源节点下的坐标分量xij为

式中，Sij为无功源节点j的注入无功对负荷节点i电压的控制灵敏度。Sij的求解过程并不是将所有无功源节点的控制灵敏度一次性求出，而是采用逐次递归法对每个无功源节点逐次求解，其物理意义反映了在获取只调节本无功源节点无功的前提下，其他负荷节点的电压响应情况。

由欧几里得距离定义可得任意两个待分区节点v、w之间的电气距离Dvw为

式中：xvg为节点v在第g个无功源节点下的坐标分量；xwg为节点w在第g个无功源节点下的坐标分量。

显然，系统中对无功源变化响应趋势一致或相仿的各负荷节点将比较集中的表现为一簇，从理论上满足聚类分析的要求。

1.3 基于层次聚类分析的配电网分区

电压控制分区问题可归类为一种典型的聚类问题，即生成一组负荷节点的集合，这些节点与同一类中的节点彼此“相似”，与其他类中的节点彼此“相异”。本文采用基于Ward距离的凝聚型层次聚类法指导分区，该方法保证了每次合并中同一类的离差平方和最小，在工程实践中广泛应用。

设共有y个待分区节点，某一类内z个节点的离散程度指标ESS及合并“成本”C可表示为

式中，xi为一维情况下节点i的位置信息，i=1，2，…，z。

基于Ward距离的聚类分析步骤如下：

步骤1每个待分区节点自成一类，即共有y组，此时每个组内的ESS值均为0；

步骤2将所求y个ESS值求和得到第1次合并前ESS总值；

步骤3枚举所有二项类集合，并计算合并该两类后的ESS总值；

步骤4选择所有二项类中合并“成本”最小的两类合并；

步骤5重复上述过程直至y减少为1。

依据类间合并的Ward距离，绘制出类个数与合并成本树状图，观察合并过程中出现的平缓期来决定合适的分类个数。

2 含DG的配电网动态无功优化与自律控制

2.1 多目标无功优化的数学模型

2.1.1 目标函数

为保证配电网运行的安全性、经济性和稳定性，本文以最小网损、最小电压偏差及最低无功补偿设备调节成本为优化目标，同时考虑逆变型DG的接入，建立含DG的配电网多目标动态无功优化模型。

1）网损

从配电网经济运行角度分析，最常采用的单目标函数是最小有功网损，该目标函数可表示为

式中：k为与节点i直接相连的节点集合；Ui(t)、Uj(t)分别为t时刻节点i、j的电压；Gij、θij分别为节点i、j之间线路的电导及电压相位差。

2）电压偏差

由于负荷的不断变化、DG的大量接入时刻对网络电压的分布产生影响。因此，为保证电压维持在满意的范围内，以节点最小电压偏差作为优化的子目标函数，即

式中：Ui(t)为t时刻节点i电压值；Uexpi(t)为t时刻节点i电压期望值。

3）无功设备的调节成本

降低无功补偿设备的调节成本有利于系统的经济运行，在实际配电网进行无功优化过程中，因调整设备而产生的投切成本和操作人员的运维工作量才是优化调节代价的主要部分。本文以功率形式对该部分调节代价进行量化并得到最小调节成本目标函数，即

式中：nQ为接有无功补偿设备的节点总数；Δbq(t)为t时刻无功补偿节点q离散控制变量的变化列向量；CUST为补偿设备单位投切成本，在不考虑故障损失的前提下，本文取CUST=1.6¥/次[9]。

2.1.2 约束条件

1）等式约束

在配电网无功优化中，各节点有功、无功功率平衡条件约束为

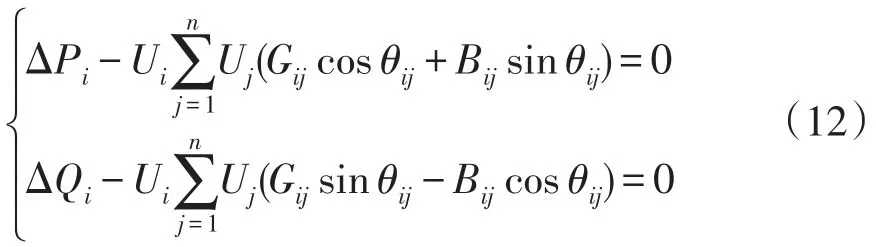
式中：ΔPi、ΔQi分别为节点i负荷和DG的有功、无功叠加；Bij为节点i、j之间线路的电纳。

2）不等式约束

本文选取t时刻并联电容器组的投切组数Cct，以及DG的无功出力Qgt作为控制变量，负荷节点电压Ut作为状态变量。具体约束可表示为

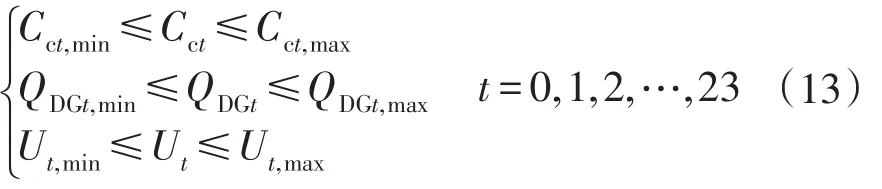
式中：Cct,max、Cct,min分别为t时刻各并联电容器节点投切组数上、下限；QDGt,max、QDGt,min分别为t时刻各DG节点无功注入上、下界限；Ut,max、Ut,min为t时刻各节点的电压最大、最小值。

2.2 基于熵权及多层次模糊综合评价理论的综合赋权法

在进行多目标决策时，各子目标权重的计算方法是其核心问题之一。其中，基于熵权理论的客观决策法认为，目标数据的离散程度越大，所占的权重也就越大，由此方法确定的各子目标权重较为客观，但所得到的结果往往因决策者偏好的不同而与期望的结果大相径庭。而在基于多层次模糊综合评价理论的主观决策方法中，通过决策者对属性的偏好确定各项评价指标的权重，具有相当大的主观性，不能准确展现各子目标间客观博弈的结果。因此，为在充分考虑系统实际运行状态的同时避免主观偏好的影响，本文提出一种基于熵权及多层次模糊综合评价理论的多目标决策方法，整体计算步骤如下。

步骤1对α个样本，β个指标，假设xij为第i个样本在第j个指标下的数值（i=1，…，α；j=1，…，β），由于各项指标的计量单位不同，因此要在计算综合指标之前先进行归一化处理。此外，由于正向指标和负向指标数值代表的含义不同，对正、负向指标需要采用不同的算法进行数据归一化，即正向指标为

式中，为正向指标和负向指标归一化后的第j项指标下第i个样本值。本文各子目标函数均为负向指标。

步骤2计算第j项指标下第i个样本值x′ij占该指标的比重pij，即

步骤3计算第j项指标的熵值，即

步骤4计算信息熵冗余度rj，即

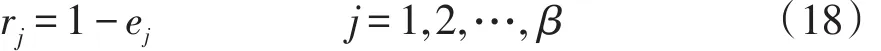
步骤5计算各项指标的客观权重系数aj，即

步骤7构建评价矩阵。考虑到系统电压控制状态各项评价指标数值是一种不断改变的过程，为准确描述各个状态控制之间的联系，本文采用梯形分布隶属度函数来表述。

（1）构建电压稳定裕度评价指标，即

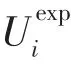
Usm的隶属度函数可表示为

将各子目标数据分别代入该隶属度函数，得到评价矩阵元素r1=[ ]r11,r12,r13。

（2）构建电压波动评价指标，即

式中，Δu表示在该种运行方式下，系统内各节点电压跨度大小，其隶属度函数可表示为

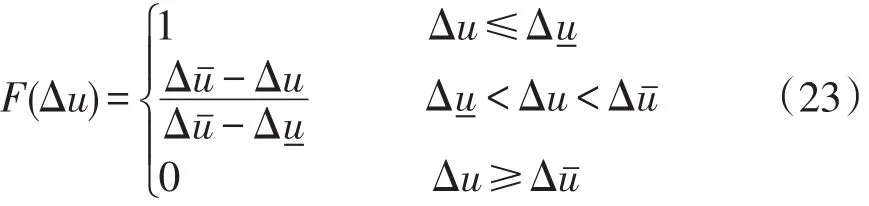
式中：Δ-u为电压波动评价优界；Δ为电压波动评价劣界。

将各子目标数据分别代入该隶属度函数，得到评价矩阵元素r2=[ ]r21,r22,r23。

（3）构建传统设备疲劳状态评价指标。出于对传统设备机械寿命的考虑，建立疲劳状态评价指标，主要考虑系统内无功补偿设备距离上次投切的时长，距离越短应避免再次启动，距离越长则倾向于动作。其隶属度函数可表示为

最终可得评价矩阵Ri

步骤8计算主观权重。选择合适的模糊合成算子计算总评价，常用的模糊算子如表1所示[16]。

表1 常见模糊算子Tab.1 Common fuzzy operators

在表1中，5种模型均有其各自的特点与适用范围，对于算子5，是先对评价矩阵Ri中的列向量做了归一化处理，再依据权重的大小对所有因素均衡统筹，评价结果能准确展现出被评对象的整体特性。因此，本文选用M（∧，+）算子，计算总评价得到主观权重bj。

步骤9计算综合权重。基于综合赋权法的各目标函数权重值λj可表示为

式中：aj、bj分别为客观权重值与主观权重值；mobj为子目标数，mobj=3。以此得到整体目标函数为

式中：λ1为子目标函数f1权重值；λ2为子目标函数f2权重值；λ3为子目标函数f3权重值。

2.3 自律控制策略

当系统出现明显电压偏差或波动时，为充分发挥补偿设备及DG的无功调节能力，本文设计了区域内电压无功自律控制策略。默认每一个区域内连接补偿设备的节点均装有本地控制器，它在监测所在节点电压情况的同时承担着与上层协同优化控制中心信息交互的任务。

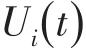
式中，α为一个大于零的常数，其取值需要避免各本地控制器同时运行后出现过高的超调，保障系统的稳定性。实验证明，令α=1/n，能保证系统对稳定性的要求[17]，本文α=1/33。

为充分考虑新能源发电的宗旨，保证DG尽可能多的发出有功功率，在电压水平控制过程中应避免改变DG的有功出力。所以在估算出额外无功调节量的基础上，结合本地无功源的容量极限，最终确定其无功出力，即：当所需无功调节量小于无功源剩余容量极限，则取无功设定值与调节量之和得到新设定值；当所需无功调节量大于无功源剩余容量极限，则取该无功源极限容量作为设定值，剩余待补偿容量由传统无功补偿装置提供。本文所提方案整体流程如图1所示。

图1 整体方案框图Fig.1 Block diagram of the overall scheme

3 算例仿真分析

3.1 基于层次聚类分析的配电网分区研究

本文采用IEEE 33节点配电系统进行仿真分析，系统额定电压为12.66 kV，三相功率基准值为SB=10 MVA，节点电压允许范围为0.95～1.05 p.u.。使用Matlab2016b编制基于牛顿拉夫逊法的潮流计算程序，得到系统节点灵敏度指标见表2。

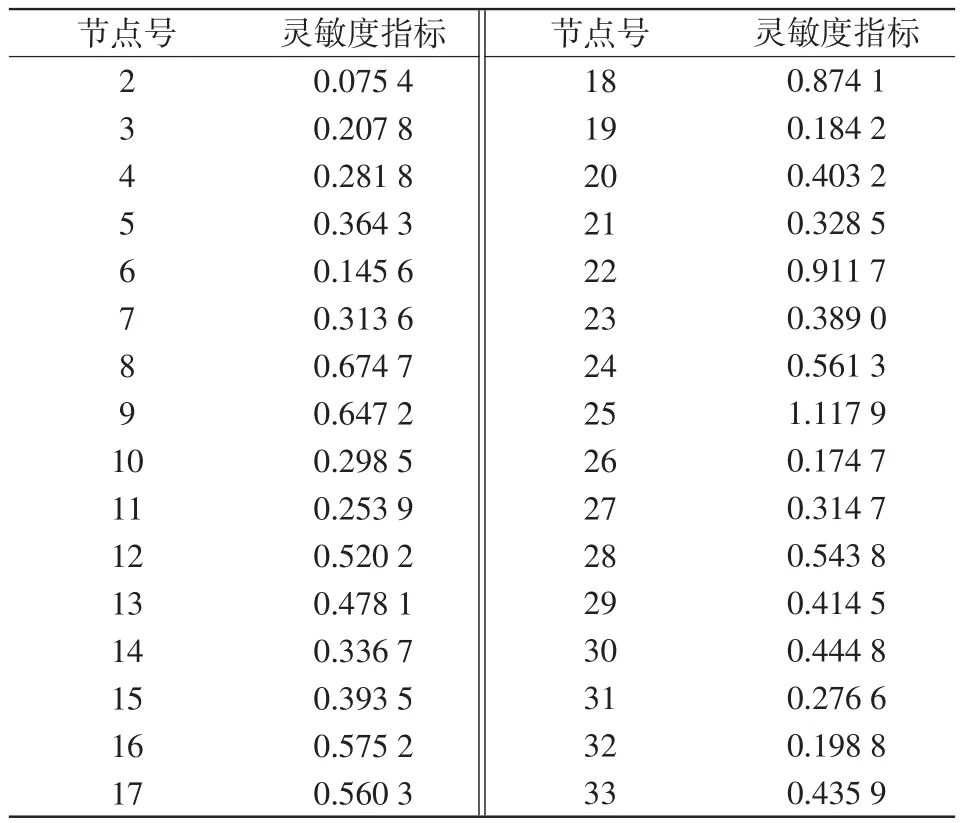
表2 节点灵敏度指标Tab.2 Node sensitivity index

由表2可知，若严格按照灵敏度大小确定中枢节点并不恰当，因系统灵敏度最大的几个节点往往是临近节点，把它们均作为中枢节点显然不符合无功功率不宜远距离传输的就地补偿原则。因此，在综合考虑灵敏度数据大小排序及中枢节点区域分布合理性的基础上，确定节点5、12、18、22、25、30为系统中枢节点，并在节点5、22、25装备5台容量为200 kVar的投切电容器组；在节点12、18装备200 kW风电；节点30装备200 kW光伏；且所接风电、光伏的无功出力均在-0.15～0.45 MVar之间，二者的典型日特性曲线和系统典型日负荷曲线如图2所示[18]。此时风、光电以中枢节点接入的方式，保证新能源在最大有功输出的基础上，充分发挥其参与配电网无功调度的能力，配合传统补偿装置，在满足薄弱节点动态无功需求的同时，实现配电网运行的综合优化。

图2 日负荷曲线及风、光日特性曲线Fig.2 Daily load curve，and daily characteristic curves of wind and photovoltaic power

在本文所提电气距离定义的基础上，利用凝聚的层次聚类算法，对改进后的IEEE 33节点系统进行分区研究，采用的分区方式为先负荷节点、后无功源节点。首先，按照各负荷节点之间的距离特性进行分区；然后，对无功源节点依照“最小连通性”原则进行合并[19]，图3给出了基于Ward距离系统的聚类过程。由图3可知，对于每次合并，可以从横轴获得合并的节点序号，而纵轴给出了本次合并的“成本”。因此，当从6分区到5分区的过渡过程中，出现了较长时间的平缓期，这意味着需要较高的合并“成本”才可将6分区聚类到5分区，即将本系统分解为6个区域能保证各区域内的强耦合性和各区域间的弱耦合性。因此改造后的IEEE 33节点系统分区如图4。

图3 IEEE 33节点系统层次聚类过程Fig.3 Hierarchical clustering process of IEEE 33-node system

图4 改造后IEEE 33节点系统分区Fig.4 Partition of IEEE 33-node system after transformation

3.2 多运行场景下综合赋权法分析

全局协同优化部分在考虑系统经济性的同时兼顾系统电压稳定性。为避免算法迭代求解时间长、易陷入局部最优解等问题，满足系统对实时性的要求，本文采用快速粒子群算法进行优化计算，其中各参数设置如表3所示。

表3 快速粒子群算法各指标取值Tab.3 Value of each index of the APSO algorithm

为验证本文所提综合赋权法的有效性，对4个权重选取场景进行比较，分别为传统权重法[20]、模糊综合评价法确定权重、熵权法确定权重、综合赋权法确定权重4个权重选取场景进行比较，并表示为场景1～4。各场景下子目标权重系数大小如表4所示，各时段系统网络损耗及电压偏差情况如表5所示。

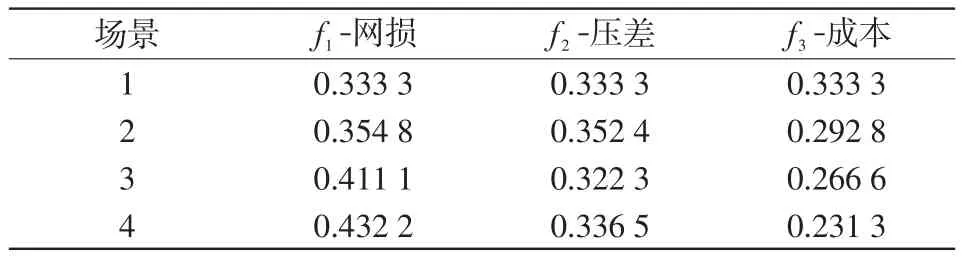
表4 不同场景下权重取值Tab.4 Weight values in different scenarios

表5 4种场景下各时段系统网络损耗及电压偏差Tab.5 Network loss of system and voltage deviation at different time intervals in four scenarios

4种场景下的网络损耗降低结果、电压偏差及无功设备调节成本情况见表6。

表6 不同场景下网损降低、电压偏差及调节成本情况Tab.6 Data of decrease in network loss，voltage deviation，and regulation cost in different scenarios

由表5、表6可以看出，在网损降低方面，4种场景下的损耗降低分别为6.27%、14.77%、14.76%和15.14%，其中综合赋权法结果最优；在电压偏差及调节成本方面，相较于其他3种场景，本文所提的综合赋权法均获得最低值，验证了该方法的正确性与有效性。

3.3 典型工况下自律协同控制方案分析

为验证本文配电网自律协同控制方案的有效性，采用改造后的IEEE 33节点系统及多目标综合赋权法进行仿真分析。上层控制中心根据系统实时运行情况执行全局无功优化程序，优化前后的各节点电压曲线如图5所示。

图5 优化前后系统节点电压曲线Fig.5 Node voltage curve of system before and after optimization

由图5可知，优化前后系统的节点电压水平有较明显的提高，但各时段的电压波动出现了不同程度的增加，这是由于DG的出力具有随机性和波动性。

各分区内无功源节点的本地控制器，依据上层控制中心优化计算所下发的电压参考值指令进行本地自律控制。取典型工况5：00、16：00和20：00，3个时刻系统各个节点的电压情况和各无功源的无功出力情况分别如图6～8所示。

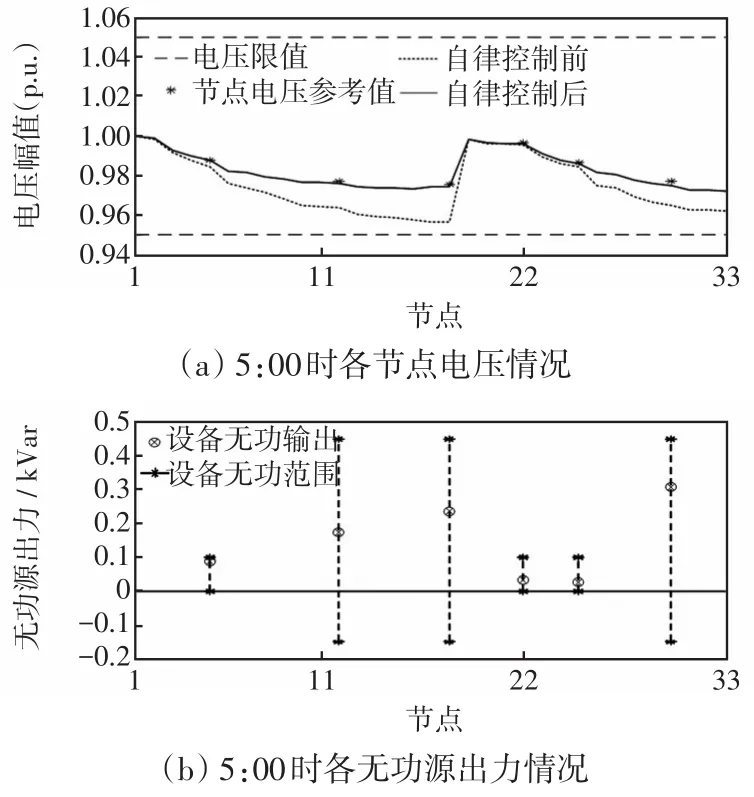
图6 5：00时节点电压和各无功源无功出力情况Fig.6 Node voltage and reactive power output from each reactive power source at 5：00

由图6可知，5：00时因其负荷较小，在本地自律控制前电压值相较于16：00、20：00较高，但仍然有部分节点电压跌破0.96 p.u.，基于各无功源的本地自律控制启动后，实现系统各节点电压对参考值的良好跟踪。在午高峰与晚高峰过渡的16：00，本地自律控制前系统各节点电压进一步下跌，个别节点电压跨越下限值，系统内电压跨度加大；由图7可知，加入本地自律控制后，各区域内无功源无功出力保证电压紧跟上层控制参考电压值；由图8可知，在20：00时，到达晚高峰，电压质量恶劣情况加剧，更多的节点电压跨越下限值，系统内电压跨度进一步加大，但上层优化结果显示，此时段无功缺额较16：00时略有下降，随着本地自律控制的启动，尽管有多个节点电压值逼近下限，存在越限的风险，但依旧把系统电压稳定在合理范围内。由以上3个典型工况可以看出，在实现对电压参考值跟随的同时，各无功源依旧留有较大裕度，反映系统具备解决更加严重电压质量问题的潜力。

图7 16：00时节点电压和各无功源无功出力情况Fig.7 Node voltage and reactive power output from each reactive power source at 16：00

4 结语

本文针对在配电网负荷、DG出力变动情况下电压质量，以及传统无功补偿装置与DG的协同控制问题进行研究，提出一种考虑DG接入的配电网自律-协同控制方案。首先，建立基于系统阻抗型节点电压方程的灵敏度指标，讨论基于无功源控制空间的配电网分区。其次，在多目标动态无功优化求解过程中提出一种基于熵权及多层次模糊综合评价理论的综合赋权法，以优化结果指导本地自律控制，实现“全局协同优化”和“分区自律控制”的协调配合。最后，以改造的IEEE 33节点配电网系统进行仿真验证，结果表明：

（1）依据系统电压/无功灵敏度指标，构造基于无功源控制空间的聚类分析，结合欧式电气距离定义及Ward类间距定义，提出电压质量控制分区的实施方案，完成针对改造后IEEE 33节点配电网的准确分区，为配电网电压质量问题的解决打下基础。

（2）本文所提基于熵权及多层次模糊综合评价理论的综合赋权法，相较于其他几种传统权重确定方法，网损降低百分比最高，电压偏差及传统设备调节成本最小，能有效提高系统的经济性与稳定性。

（3）本文提出的自律协同控制方案具有良好的收敛性、实时性和鲁棒性。仿真结果表明，针对3个典型工况，本方案充分发挥了DG快速反应、快速补偿的优势，实现了DG与传统无功补偿装置的协同控制；在保证系统电压质量稳定在合理范围内的同时留有裕度，具备应对更加复杂电压质量问题的潜力；同时对今后逆变型DG主动参与电压质量控制的研究与应用具有一定的指导价值，可在实践中不断优化，具有持久的意义。