基于量测数据贝叶斯概率矩阵分解的变压器运行状态监测方法

2022-01-27郭凌旭张文旭

电力系统及其自动化学报 2022年1期

程逍，李平，郭凌旭，张文旭

（1.国家电网有限公司，北京 100120；2.国网天津市电力公司，天津 300010；3.天津大学智能电网教育部重点实验室，天津 300072）

电力变压器是电力系统中十分重要的设备，它的安全运行与电力系统的安全可靠供电息息相关。变压器在运行过程中，由于局部放电，高温过热等故障，会在变压器油中释放出各种气体，并溶解于油中。对这些气体含量的监测和比例分析，可评估变压器的运行状态，以及发现变压器中可能存在的故障[1-4]。因此对变压器油中溶解气体浓度变化的趋势进行预测，可及早发现变压器可能出现的故障和缺陷，为变压器的安全运行提供保障[5]。

油中溶解气体预测的方法有很多，例如，基于时间序列ARIMA（autoregressive integrated moving average）模型的预测方法[6]，以及基于灰色模型GM（grey model）[7]的预测方法等传统方法，其中，ARI⁃MA模型预测方法对时序数据稳定性有一定要求，本质上只能捕捉线性关系，对于非线性关系处理能力较差；而灰色模型只适应于指数增长的预测。最近兴起的数据驱动[8]人工智能方法逐渐应用在电力系统的智能辨识[9]、模型预测等方面，该方法可通过训练寻找输入与输出之间的关系，构建预测模型，实现对油中溶解气体的预测。常用的传统人工智能方法有支持向量机SVM（support vector ma⁃chine）[10]、人工神经网络 ANN（artificial neural net⁃work）[11]、极限学习机 ELM（extreme learning ma⁃chine）[12-13]等，但传统人工智能方法在寻找时间序列关联趋势、捕捉时序信息方面存在不足，因此预测效果较差。循环神经网络RNN（recurrent neural network）[14]因具有循环反馈结构，更适合处理时序数据，在时间序列预测方面有着很好的应用，但其在对长时间序列进行训练时会出现梯度消失，梯度爆炸等情况。长短期记忆LSTM（（long short-term memory）神经网络通过引入记忆门控单元对RNN进行改进，解决了上述问题，得到广泛的应用[15]。

由于实际监测中数据缺失是不可避免的现象，而针对油中溶解气体缺失数据填补方面的研究还相对较少。贝叶斯概率矩阵分解BPMF（Bayesian probabilistic matrix factorization）[16]是一种基于高斯分布的数据缺失值填补方法，它可以通过马尔科夫蒙特卡洛的方法，对基函数矩阵和系数矩阵的不同超参数的结果进行模拟，并计算不同参数下缺失数据填补结果的概率密度函数，自适应选取最优的缺失数据填补结果。

鉴于此，本文提出一种基于BPMF和LSTM神经网络的油中溶解气体浓度预测方法。首先，通过BPMF对油中溶解气体的缺失数据进行填补；然后，利用皮尔森相关系数PCC（Pearson correlation coeffi⁃cient），筛选与目标输出相关性高的气体特征作为输入；最后，建立LSTM神经网络的预测模型，通过贝叶斯优化的方法对LSTM神经网络的超参数进行寻优，并通过实例分析得到了很好的预测结果。

1 数据预处理

鉴于油中溶解气体实际量测过程中会有数据传输异常，数据缺失等问题，本文考虑首先采用局部异常因子LOF（local outliers factor）的方法进行异常值检测；然后，将异常值置为空，采用BPMF的方法对数据缺失值进行填补；最后，对数据进行标准化处理，并采用PCC的方法对输入气体特征进行筛选，完成数据预处理。

1.1 异常值检测

油中溶解气体数据实际采集过程中难免出现噪声或干扰问题，导致出现明显偏离正常值的异常数据，干扰训练过程，破坏预测结果，因此要对其进行筛除。本文采用LOF算法对数据异常值进行检测，该算法是一种非监督类型的算法，基于密度对数据异常值进行筛选，将任何给定数据的密度与其邻居的密度进行比较，如果其密度相对于它的近邻低得多则视此数据为异常点。鉴于文章篇幅所限，具体方法和原理见文献[17]。

1.2 BPMF原理

当变压器油中溶解气体的监测装置出现故障，或者停电检修时，会引起数据缺失的问题，这时需补全缺失数据以更好地利用数据。BPMF是一种优秀的缺失数据填补方法，其实质是基于已有数据对缺失数据的预测，基本原理如图1所示。

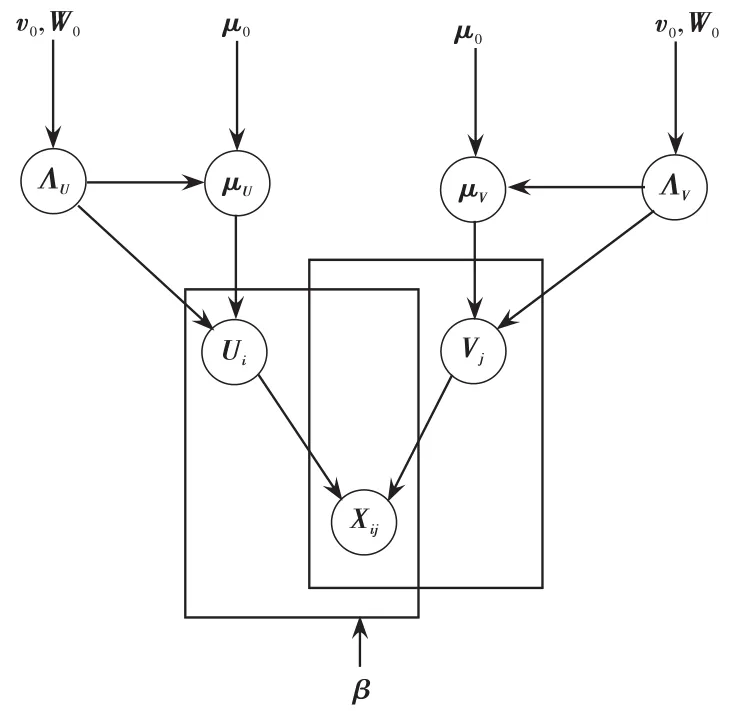
图1 BPMF原理Fig.1 Schematic of Bayesian probability matrix factorization

设置带有缺失数据的油中溶解气体浓度数据矩阵X为n行m列矩阵，将X分解为

式中：U为基函数矩阵；V为系数矩阵。

假设U与V服从高斯分布，即

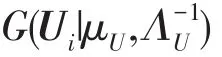
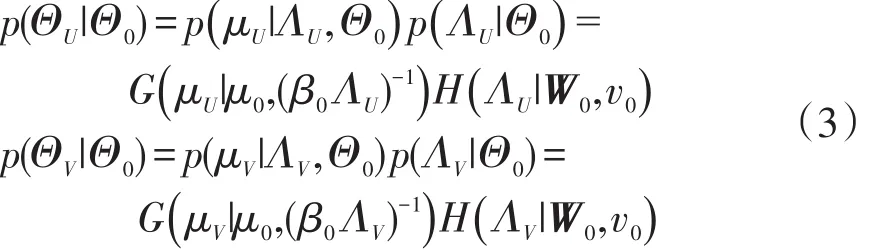
应用该方法进行油中溶解气体缺失数据填补的本质就是利用可能出现的超参数组合分别进行缺失数据填补，然后对所有结果进行加权求和，加权系数就是每个超参数组合对应的概率密度函数。在马尔科夫蒙特卡洛MCMC（Markov chain Monte Carlo）的框架下，其计算公式为

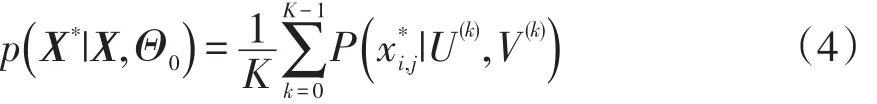
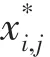
采用吉伯斯抽样[18-19]的方法对式（4）进行采样，通过迭代的方式更新超参数组合、基函数矩阵和系数矩阵，完成数据填补。其具体流程如下。

步骤1初始化基函数矩阵U和系数矩阵V。

步骤2更新超参数ΘU和ΘV，H为具有自由度和k×k比例矩阵的Wishart分布，由于基函数矩阵和系数矩阵属于同类型分布，因此计算方法相同，以基函数矩阵的超参数为例，其计算公式为

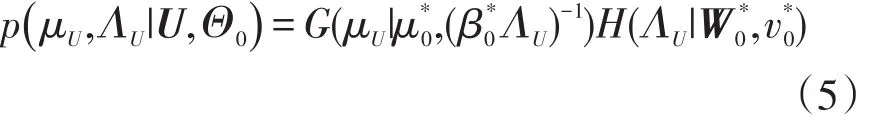
式中：

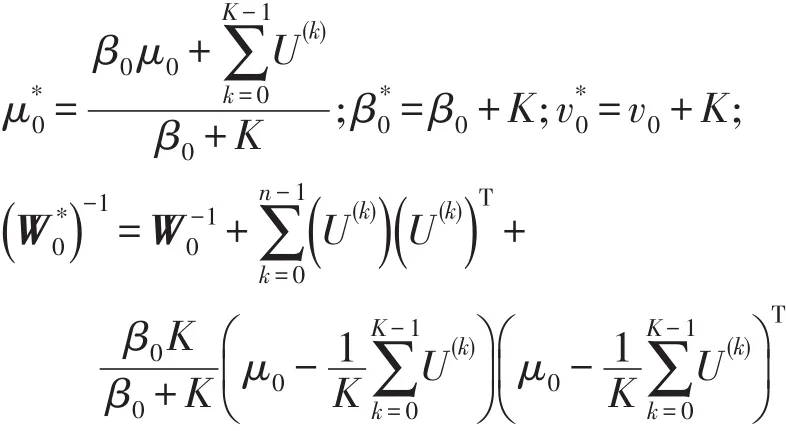
步骤3更新基函数矩阵U和系数矩阵V。根据贝叶斯公式可得基函数矩阵更新公式为

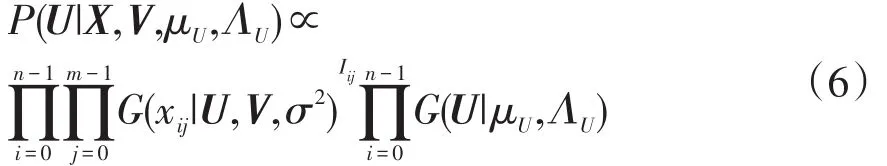
式中：σ2为矩阵X方差；xij为矩阵X的第i行j列元素。Iij标记数据是否缺失，当xij=0时（即为该位置产生缺失值），Iij=0；当xij=1时，Iij=1。同理可得系数矩阵V的更新公式，m为矩阵X行数，n为矩阵X列数。

步骤4设置最大迭代次数使其收敛，重复步骤2、步骤3直至到达最大迭代次数，完成油中溶解气体缺失数据的填补。本文设置最大迭代次数为1 000以保证收敛。

1.3 皮尔森相关系数

变压器油中由于不同情况，不同原因会分解出不同的气体，其中部分气体存在着强相关性，部分气体存在着弱相关性。因此可应用PCC对输入特征进行筛选，过滤掉弱相关特征，将强相关特征作为输入，这样可以提升训练速度，并提高预测的准确率。

特征Q和特征R的PCC可表示为

式中：Cov(Q,R)为协方差；σQ、σR分别为特征Q、R的方差。

当PCC大于0时，两个特征正相关；当PCC小于0时，两个特征负相关；其绝对值越大，相关性越强。

2 LSTM神经网络

LSTM神经网络也是一种RNN。LSTM神经网络通过引入记忆模块，改进了普通RNN序列过长时会出现梯度爆炸或梯度消失问题，得到广泛的应用。

2.1 LSTM神经网络原理

LSTM神经网络结构如图2所示。

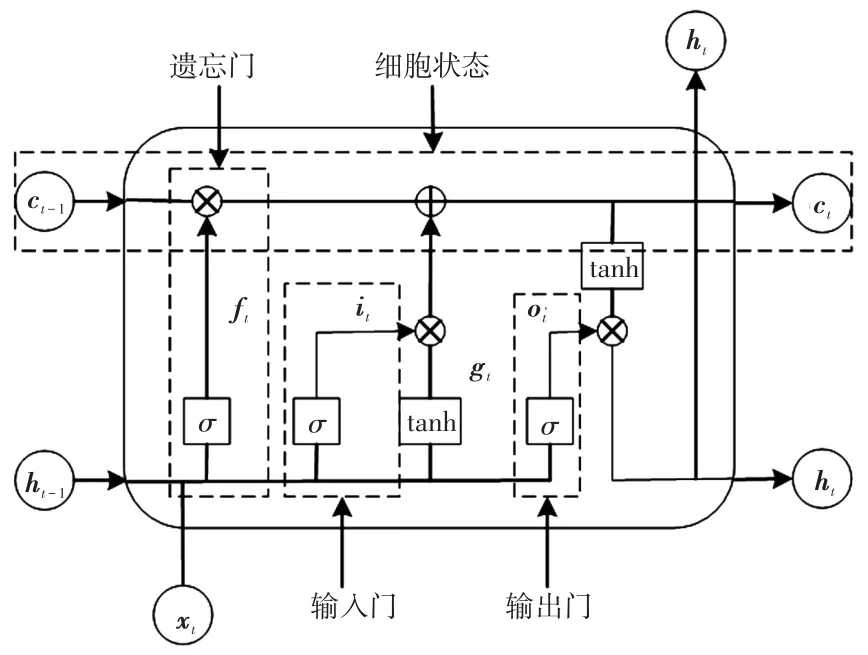
图2 LSTM神经网络结构Fig.2 Structure of LSTM neural network

由图2可知，LSTM神经网络主要由遗忘门、输入门、输出门组成，通过对门的控制，控制长时间序列信息的保留与丢弃，记住重要信息，遗忘不重要的信息。LSTM包含3种输入：xt为当前时刻输入的油中溶解气体序列；ct-1为前一时刻细胞状态，包含长期记忆的信息；ht-1为前一时刻输出序列，包含短期记忆的信息。其中，tanh激活函数将输入压缩到[-1，1]之间；sigmoid函数将输入压缩到[0，1]之间；遗忘门可以决定如何丢弃信息；而输入门可以决定如何更新细胞状态；输出门用来决定当前的输出状态。具体计算过程为

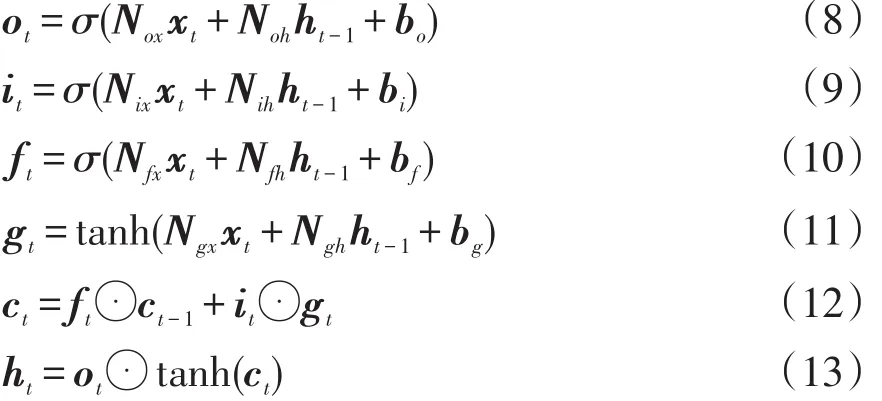
式中：σ为sigmoid激活函数；⊙为各元素按照位置相乘；ot、it、ft和gt分别为输出门、输入门、遗忘门和细胞状态的输入在当前时刻t的计算结果；ct为当前时刻t的细胞状态；ht为当前时刻t的输出序列；Nox、Noh；Nix、Nih；Nfx、Nfh；Ngx、Ngh分别为输出门、输入门、遗忘门和细胞状态的权值矩阵（即Nox为ot和xt之间的权值矩阵，其他矩阵同理）；bo、bi、bf、bg分别为输出门、输入门、遗忘门和细胞状态的偏置。

2.2 超参数寻优

超参数指人工智能方法中需要手动设置，对训练效果和预测效果有着很大影响的参数。例如，学习率、迭代次数、批次尺寸、神经网络隐含层数、隐含层神经元个数等。调参是建立人工智能模型时非常重要的一步，参数选择对于模型效果有着很大的影响。

贝叶斯优化方法[20]使用代理函数拟合超参数组合与模型评价的关系，在选取下一组超参数前会参考之前的结果，克服网格搜索和随机搜索的盲目性，该方法寻优效果更好，得到了广泛的应用。

本文选用贝叶斯优化[21]方法对LSTM神经网络的超参数进行寻优。LSTM设置初始学习率为0.001，利用python环境下keras库的自适应学习率在学习过程中更新学习率，选取自适应矩估计优化器，均方误差损失函数。通过利用控制变量的方法，发现在双隐含层时预测效果最好，故选择双隐含层。因此，利用贝叶斯优化方法对第一层隐含层的神经元个数（即unit1）、第二层隐含层的神经元个数（即unit2）、批次尺寸（即Batch_size）和迭代次数（即Epoches）进行超参数寻优。

3 BPMF-PCC-LSTM预测模型

针对变压器油中溶解气体实际量测过程中，由于监测装置故障，数据传输信号中断，或对异常值进行筛除均会出现缺失值的情况，本文采用基于BPMF的方法填补缺失值，结合PCC和LSTM神经网络，构建油中溶解气体浓度预测模型如图3所示，具体流程如下：

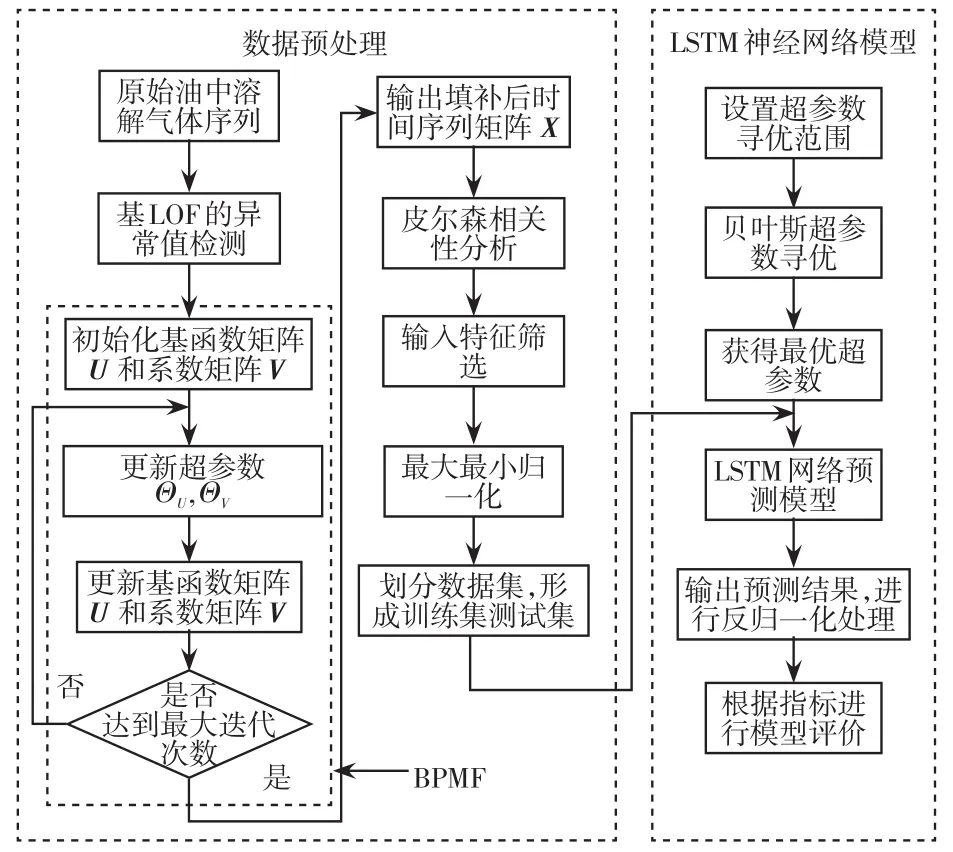
图3 油中溶解气体浓度预测模型Fig.3 Prediction model of dissolved gas concentration in oil

步骤1将油中溶解气体序列运用LOF的方法进行异常值检测，将异常值置为空；

步骤2将异常检测后的数据运用BPMF的方法进行缺失数据填补；

步骤3对缺失数据填补后的油中溶解气体序列计算PCC，筛选强相关的气体特征作为输入；

步骤4对油中溶解气体序列进行最大最小归一化，并划分出训练集与测试集，归一化公式为

式中：x为某种气体；xmin为某种气体最小值；xmax为某种气体最大值。

步骤5针对不同的气体预测，分别进行基于贝叶斯优化的超参数寻优；

步骤6根据超参数寻优结果分别搭建LSTM预测网络模型，进行模型训练；

步骤7进行模型测试和误差分析。

4 算例分析

本文选取某变压器2020年2月18日—2020年12月9日的油中溶解气体监测数据作为数据集，由于乙炔气体含量一直为0，故不考虑该气体，将乙烷、甲烷、乙烯、氢气、一氧化碳、二氧化碳、总烃的数据作为算例分析数据集。数据监测周期为1 d，共295组数据，按照时间顺序选取前230组数据作为训练集，后65组数据作为测试集。

4.1 数据预处理

首先应用LOF方法对数据进行异常值检测，将异常值设置为空值，当做缺失值看待。然后应用BPMF的方法对数据的缺失值进行填补。本文所选取缺失2020年6月7日—2020年7月9日、2020年11月1日—2020年11月8日的数据，以甲烷为例，预处理前甲烷浓度如图4所示，预处理后甲烷浓度如图5所示。

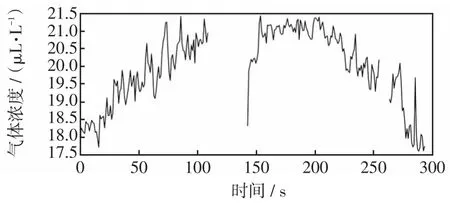
图4 预处理前甲烷浓度Fig.4 Concentration of methane before pretreatment

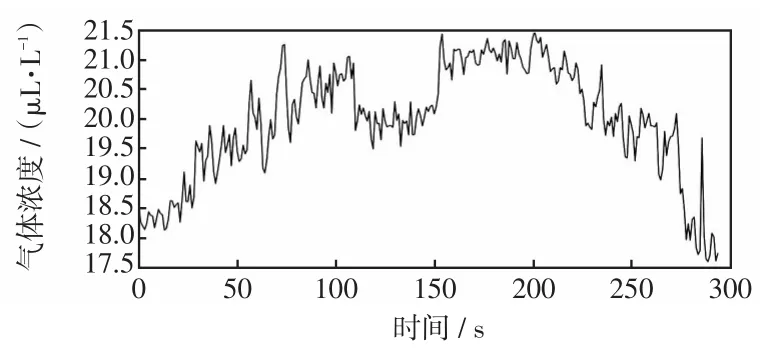
图5 预处理后甲烷浓度Fig.5 Concentration of methane after pretreatment

由图4～5可知，BPMF方法能够很稳定的填补时间序列缺失值，不会产生很大波动，显示了BPMF方法的优越性。

4.2 特征筛选

本文采用PCC对油中溶解气体进行相关性分析，PCC见表1。由表1可以看出乙烯、甲烷、乙烷、总烃之间存在着较强的相关性，这是因为这些气体里大部分是因为过热故障而产生的，因此存在着关联性。在预测某种气体时，选取与该气体PCC绝对值在0.7以上的特征作为预测模型的输入特征。

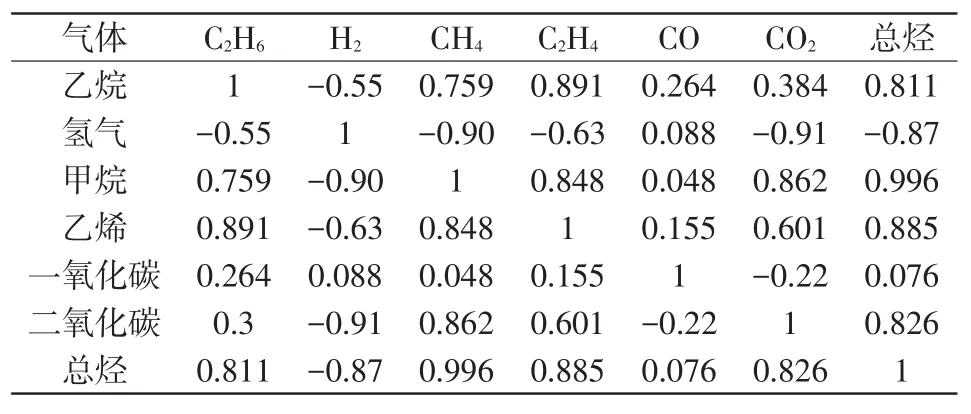
表1 皮尔森相关系数Tab.1 Pearson correlation coefficients

4.3 评价指标

为验证本文所提出方法的准确性，选择平均绝对百分比误差MAPE（Mean Absolute Percentage Er⁃ror）和均方根误差RMSE（Root Mean Squared Error）作为评价指标，即

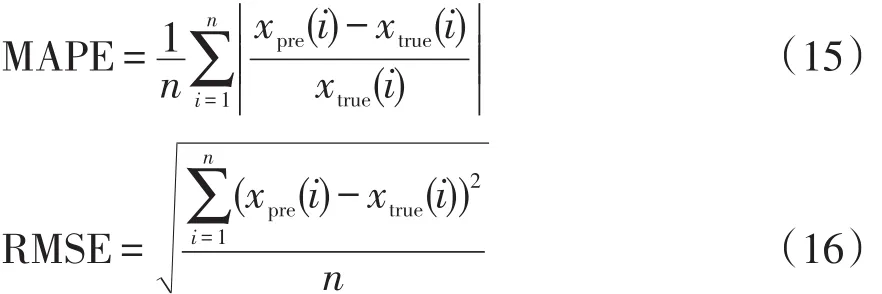
式中：xtrue(i)为测试集样本i的实际值；xpre(i)为测试集样本i的预测值；n为测试集样本容量。MAPE和RMSE越小证明方法准确度越好，预测精度越高。

4.4 超参数寻优

在数据预处理与特征筛选的基础上，采用贝叶斯优化的方法分别对不同气体的LSTM网络预测模型的超参数进行寻优。设置第1层隐含层的神经元个数（即unit1）的寻优范围为[1，256]；第2层隐含层的神经元个数（即unit2）的寻优范围为[1，128]，批次尺寸（即Batch_size）的寻优范围为{8，16，32，64，128}；为防止过拟合，迭代次数（即Epoches）的寻优范围为[50，300]。不同气体最终寻优结果如表2所示。

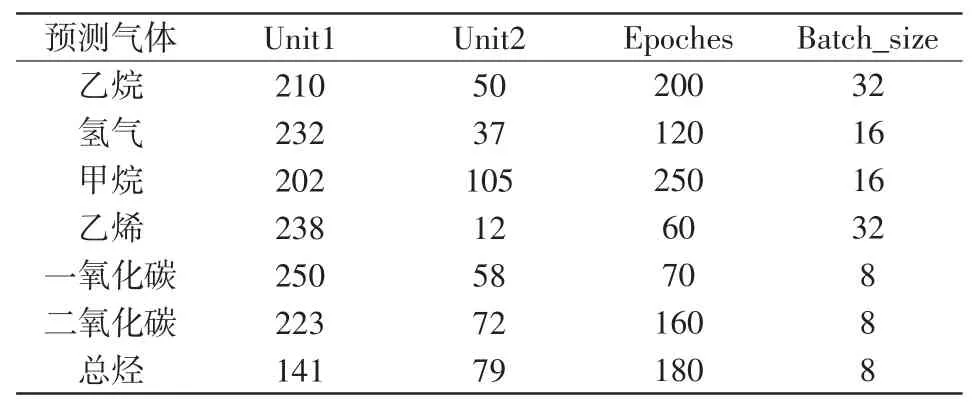
表2 超参数寻优结果Tab.2 Optimization results of hyperparameters

4.5 油中溶解气体浓度预测

利用LSTM神经网络对油中溶解气体浓度进行训练和测试。为了验证本文所提方法的优越性，将BPMF数据填补的方法和K最近邻KNN（K near⁃est neighbors）数据填补方法、多元特征数据填补方法、前值插补法、后值插补法进行对比。在缺失数据填补基础上，这些方法都应用PCC-LSTM的预测模型进行油中溶解气体预测，以达到控制变量的目的。

不同缺失值填补方法预测结果对比如表3所示，由表3可知，BPMF方法的MAPE指标和RMSE指标均最小。以氢气为例，BPMF方法的指标值相比其他4种方法，MAPE指标值分别降低了24.45%、18.58%、14.84%、23.33%；RMSE指标值分别降低了28.42%、26.09%、25.27%、28.8%，有效地提升了预测精度。KNN方法是基于相邻最近的数据来估算缺失数据的，当出现连续缺失数据时，该方法会导致相邻数据不足，以上一缺失填补值为相邻数据等情况，从而导致填补数据不准。多元特征方法是将每个缺失数据点对应特征建立为其他特征的函数，然后使用该估计进行缺失数据的插补，多特征数据连续在同一时刻缺失也会导致缺失数据填补不准。前值插补和后值插补未考虑时序性，在序列连续缺失时填补也不准确。而BPMF方法是通过吉伯斯抽样的方法对BPMF模型的超参数进行更新，自适应的选取最优结果，能够很好的完成时间序列连续缺失数据的填补，提升预测精度。

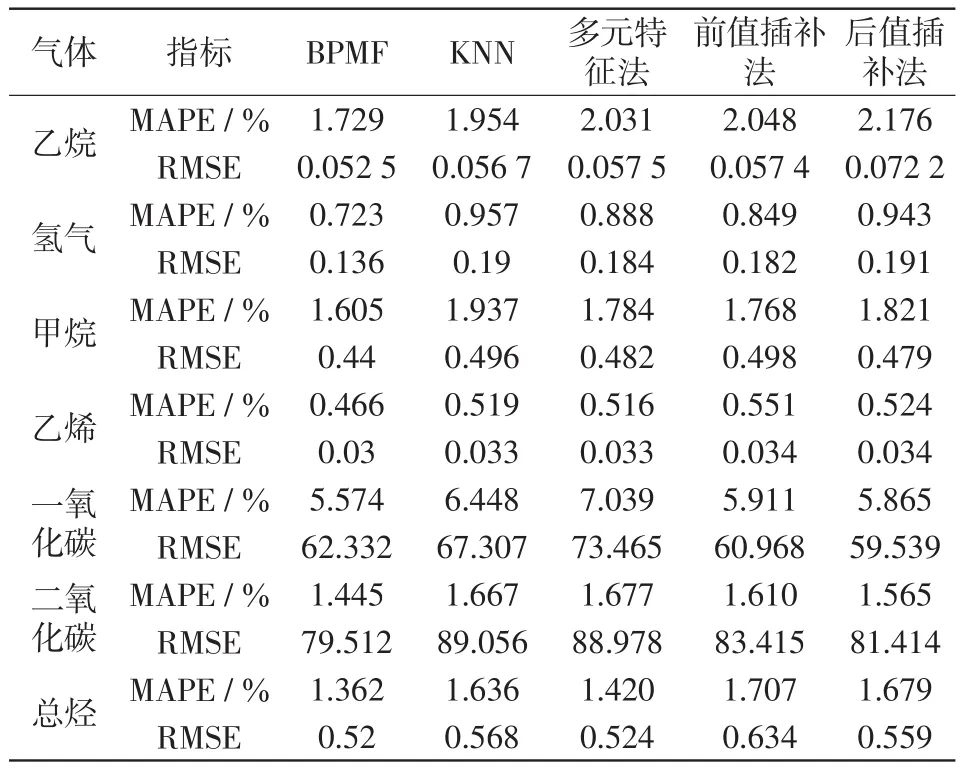
表3 不同缺失值填补方法预测结果Tab.3 Prediction results obtained using different missing value filling methods

在使用BPMF进行缺失数据填补和PCC筛选特征的基础上，建立反向传播BP（back propagation）神经网络算法、SVM算法、极限梯度提升树XGBoost（eXtreme gradient boosting）算法的预测模型，并与LSTM算法预测模型和真实值（图6～12中TRUE）进行对比。然后将应用PCC筛选特征情况下的LSTM模型和不应用PCC筛选特征（即将全部油中溶解特征气体作为输入）情况下的LSTM模型进行对比，具体预测结果如图6～12所示，指标参数见表4。

表4 不同预测模型的预测结果Tab.4 Prediction results based on different prediction models

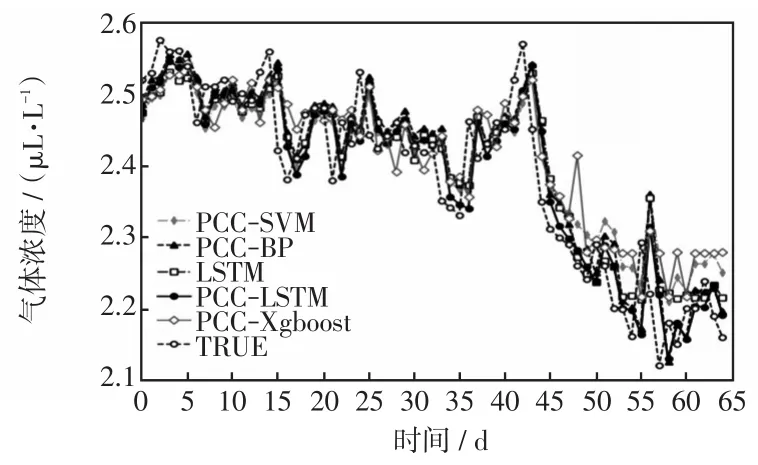
图6 乙烷预测结果Fig.6 Prediction results of ethane

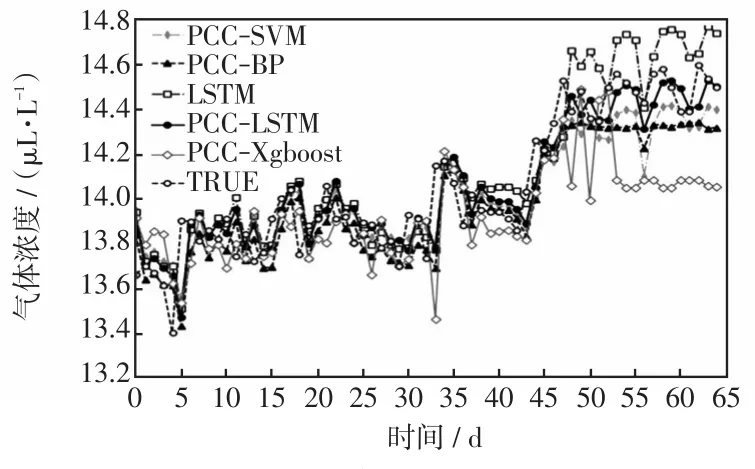
图7 氢气预测结果Fig.7 Prediction results of hydrogen

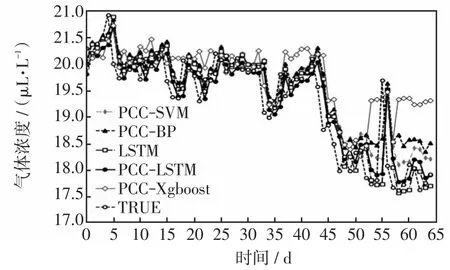
图8 甲烷预测结果Fig.8 Prediction results of methane

图9 乙烯预测结果Fig.9 Prediction results of ethylene

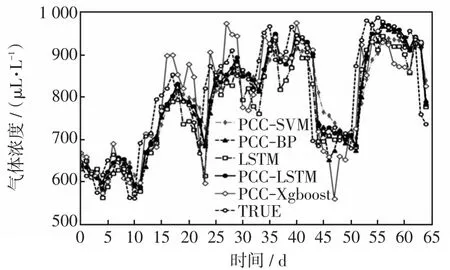
图10 一氧化碳预测结果Fig.10 Prediction results of carbon monoxide

图11 二氧化碳预测结果Fig.11 Prediction results of carbon dioxide

图12 总烃预测结果Fig.12 Prediction results of total hydrocarbon

由图6～12及表4可知，在PCC筛选基础上的LSTM预测模型比不进行特征筛选的LSTM预测模型的预测精度要高，且提升了效率。以氢气为例，PCC-LSTM方法比LSTM方法的MAPE指标值降低了24.61%，RMSE指标值降低了20.0%，PCC-LSTM完成训练的时间为20.61 s，LSTM完成训练的时间为29.39 s；同时PCC-LSTM方法相比于PCC-SVM、PCC-BP、PCC-XGBoost方法的预测准确度要高，以氢气为例，MAPE指标值分别降低了14.03%、21.16%、47.46%，RMSE指标值分别降低了8.72%、18.51%、46.46%。根据仿真结果可以看出，PCCLSTM模型的预测精度较高，有一定的实用价值。