多分类边界支持矩阵机及其在滚动轴承故障诊断中的应用*

2022-01-27马文静

机电工程 2022年1期

关键词：超平面识别率分类器

马文静,李鑫,张云

(1.河北机电职业技术学院信息工程系,河北邢台 054000;2.河南科技大学机电工程学院,河南洛阳 471003;3.洛阳轴承研究所有限公司技术中心,河南洛阳 471039)

0 引言

作为一种极其重要的基础部件,滚动轴承被广泛应用于航空发动机、数控机床、风力发电机组等各种传动系统中。但是,由于滚动轴承工作环境通常较为恶劣,其局部极易产生疲劳破坏。

当滚动轴承出现失效时,如不及时排除故障,将有可能造成巨大的经济损失或重大的安全事故。因此,滚动轴承故障诊断对保证机械系统高效、安全运行具有重要意义[1-3]。

随着人工智能的兴起,各种基于机器学习的滚动轴承故障诊断方法被陆续提出,如支持向量机(support vector machine, SVM)、人工神经网络(artificial neural network, ANN)等[4,5]。其中,SVM采用结构风险最小化(structural risk minimization, SRM)的分类策略,具有较强的泛化能力和小样本学习能力[6]。因此,SVM一直是智能滚动轴承故障诊断领域的研究热点。然而,基于支持向量机的滚动轴承故障诊断方法大都需要人工提取滚动轴承固有的故障特征,这将破坏时域信号数据之间的关联性。同时,当故障信息比较微弱时,提取特征很可能造成微弱信息的泄露,致使建立的模型失真[7]。

为了解决上述问题,LUO Luo等人[8]设计了一种矩阵形式的支持矩阵机(support matrix machine, SMM),SMM的核心思想是以矩阵的形式构造一个超平面,来划分不同的类。在SMM算法中,SMM采用核范数来控制权矩阵的秩,充分捕获嵌入到矩阵数据中的结构信息。

鉴于SMM良好的分类能力,相关学者在SMM基础上开发了一系列改进的SMM方法,如ZHENG Qing-qing等人[9]采用多分类策略提出了多分类支持矩阵机(multiclass support matrix machine, MSMM),解决了SMM多分类的问题。同时,ZHENG Qing-qing等人[10]继续探索数据的冗余性和鲁棒性,提出了稀疏支持矩阵机(sparse support matrix machine, SSMM),其通过增加L1范数来减弱冗余特征和含噪特征对建模的影响,提高了分类的精度。PAN Hai-yang等人[11]利用辛几何相似变换和最小二乘法求解决策函数,提出了辛几何矩阵机(symplectic geometry matrix machine, SGMM),增强了模型的鲁棒性和收敛性。

然而,上述SMM及改进算法所建立的超平面都是平行超平面,无法最大化两类复杂数据样本之间的距离。

针对上述问题,笔者提出一种基于多分类边界支持矩阵机(MBSMM),并应用于滚动轴承故障诊断中。

该方法通过建立多分类目标函数,利用非平行边界超平面来隔离任意两种类型的数据,非平行边界超平面可以最大化任意两类样本之间的间隔,达到预期的分类效果;同时,在MBSMM中引入逐次超松弛法(successive overrelaxation, SOR)[12],可以大大提高算法的效率。

最后为了验证MBSMM在滚动轴承故障诊断中的有效性,笔者将其与经典矩阵分类器进行比较分析。

1 多分类边界支持矩阵机

对于k类分类问题,基于k次超平面离第k类样本集越近,离其他类样本集越远的原则,笔者建立MBSMM的目标函数,其表达式如下:

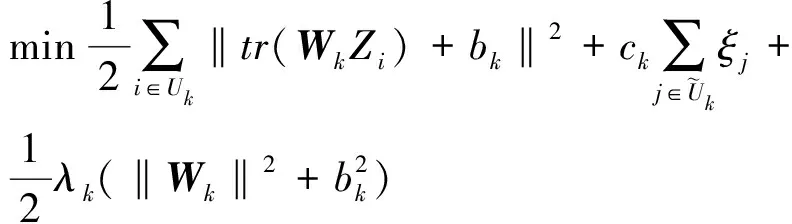
(1)

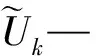
通过引入非负拉格朗日乘子α和β,实现了目标函数(1)的拉格朗日变换。其表达式如下:

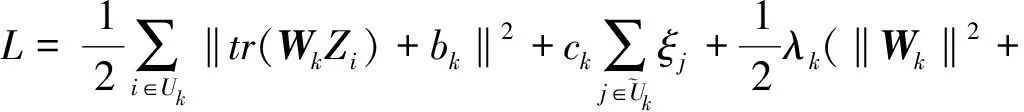
(2)

为解式(2),笔者计算了Wk、bk、ξj、αj和βj的偏导数,得到了满足Karush-Kuhn-Tucker(KKT)条件的方程:

(3)

通过整理式(3),可得:

(4)

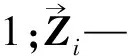
如果Yi=(ZiI)T被定义,那么有:

(5)

(6)

接下来,笔者用式(6)代替拉格朗日函数(2),得到问题(1)的对偶问题:

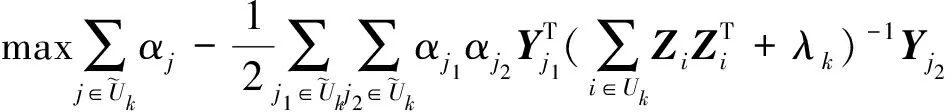
(7)

也可以表示为:

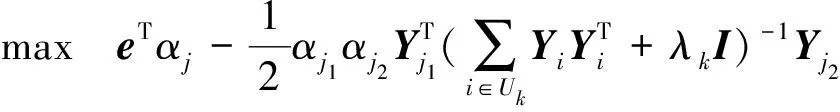
(8)

因此,求解式(1)的问题转化为对偶问题(8)中α的解,并且可由式(6)构造第k个近端超平面。

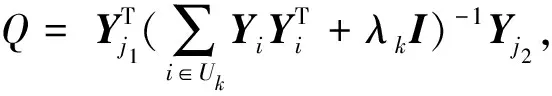
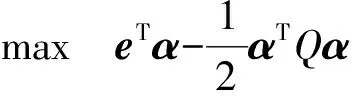
(9)

为了解决式(9)的问题,可以用SOR方法求解。同时,SOR可以线性收敛到最优值,不需要太多计算就可以处理大规模数据集,因此,笔者取收敛误差阈值0.01。

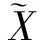
(10)

根据式(10),笔者通过比较特征矩阵和不同交互超平面之间的距离,来确定样本的类型。

2 基于相关支持矩阵机的诊断方法

当滚动轴承发生故障时,其采集的振动信号通常与正常状态下的振动信号在时域上略有不同,但是很难直接观察到故障状态,需要采用机器学习方法对采集的信号进行学习,建立状态预测模型。

基于支持向量机的滚动轴承故障诊断方法都需要人工提取滚动轴承固有的故障特征,这将破坏时域信号数据之间的关联性。同时,当故障信息比较微弱时,提取特征很可能造成微弱信息的泄露,致使建立的模型失真。

为此,笔者提出了一种基于多分类边界支持矩阵机(MBSMM)的滚动轴承故障诊断方法。该方法以矩阵为建模单元,充分利用原始信号的微弱信息建立准确的预测模型。

辛几何相似变换(symplectic geometry similarity transformation, SGST)作为一种新的信号分析方法[13],已被证明具有良好的特征提取能力。因此,笔者拟采用SGST分析原始信号,以获得可以保存完整结构信息的特征矩阵。

实验方法的过程如下:

(1)将拾取的振动信号进行辛几何相似变换,获得具有原始信号状态信息的辛几何系数矩阵;

(2)将获得的辛几何系数矩阵分为训练样本和测试样本,对训练样本进行训练并建立预测模型(10);

(3)对测试样本进行测试分类,获得分类结果。

3 实验及结果分析

3.1 实验台及参数设置

为了验证该方法的有效性,笔者选用滚动轴承故障数据进行比较与分析。实验中所使用的滚动轴承型号为SKF6205,环境温度为31 ℃,同时采用黄油润滑脂润滑。

滚动轴承故障模拟实验台如图1所示。

图1 滚动轴承故障模拟实验台

为了模拟滚动轴承不同的故障类型,笔者采用电火花加工技术,分别在轴承的内圈、外圈和滚动体上切割出不同尺寸(0.4 mm、0.2 mm和0.3 mm)的“故障”;同时,利用LMS软件在测试轴承底座上采集加速度振动信号,每类滚动轴承状态采集200个样本(一个样本包含2 048个点)。

实验条件及参数设置如表1所示。

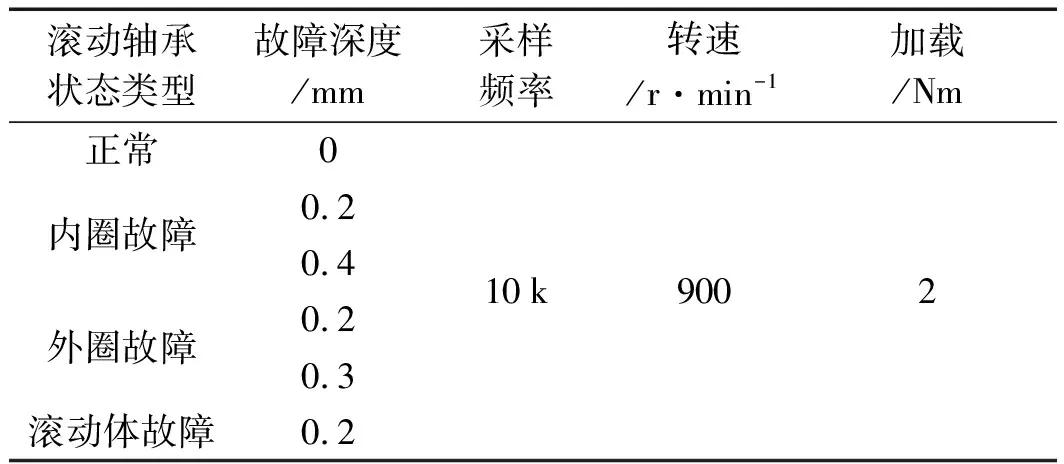
表1 实验条件及参数设置

3.2 实验结果分析

在实验验证过程中,为了避免单次实验的偶然性,笔者随机抽取100个训练样本和100个测试样本,进行5次独立的测试实验。

同时,笔者对SGMM、SSMM和MSMM进行了比较分析。

4种分类器的测试结果如图2所示。

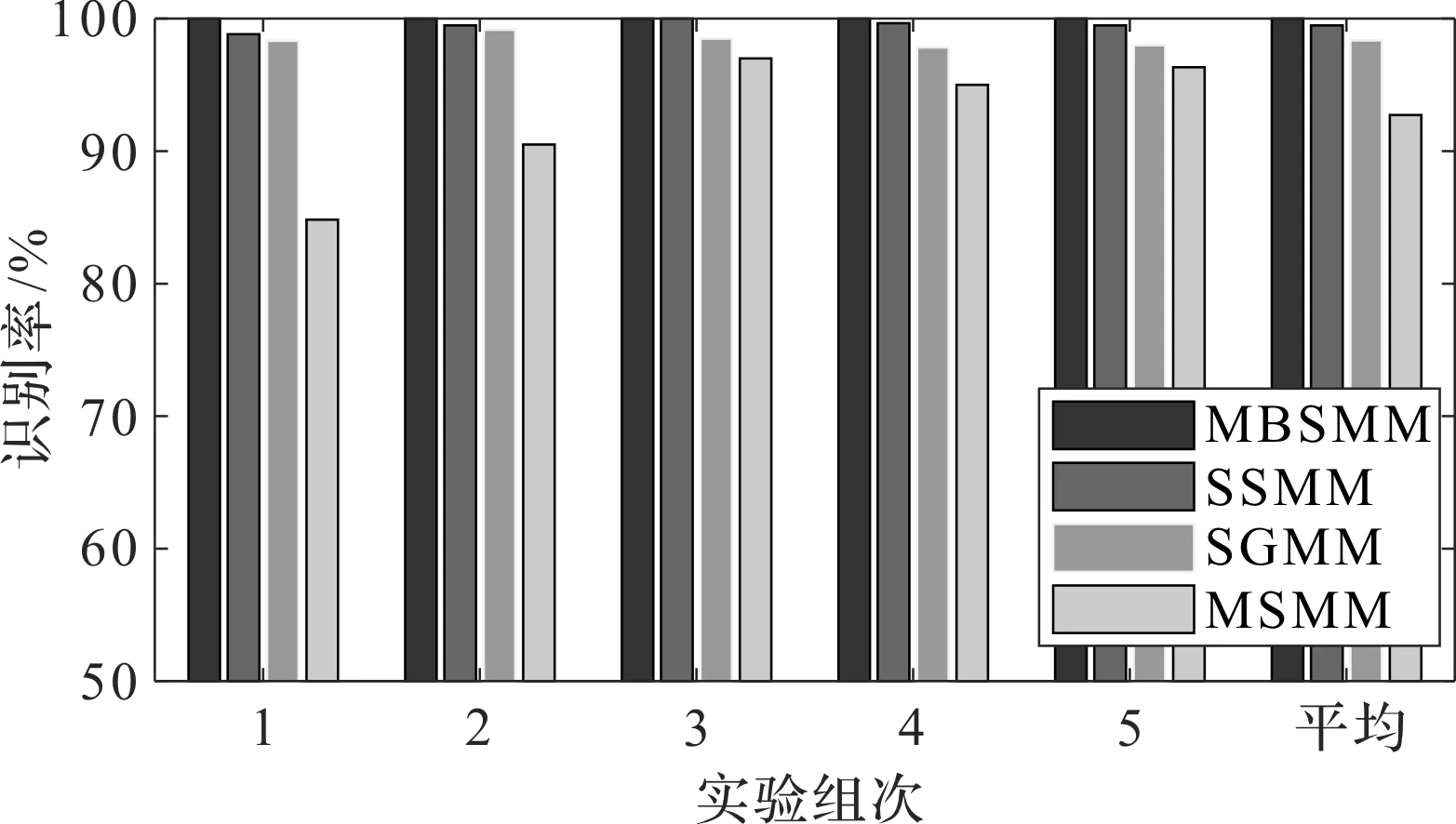
图2 4种分类器的识别结果

由图2可以看出:

在每次试验中,MBSMM对滚动轴承状态监测的识别率均最高,说明所提方法在滚动轴承故障诊断中具有较大的分类优势;

在所有方法中,MSMM的故障诊断效果最差,这是由于MSMM对数据的要求较高,数据复杂度和数据长度会导致MSMM不收敛;

SGMM具有较好的鲁棒性,测试结果表现良好,但该方法没有考虑信号的稀疏性;

SSMM具有较高的识别率,其具有较强的泛化能力和鲁棒性。然而,SSMM不能捕捉到原始振动信号的结构信息,同时该方法的本质是建立平行超平面,完成不同类型数据的划分,无法得到令人满意的结果。

综上所述,与MSMM、SGMM和SSMM相比,所提方法可通过建立多分类目标函数,利用非平行边界超平面来隔离任意两种类型的数据,非平行边界超平面可以最大化任意两类样本之间的间隔,达到预期的分类效果。因此,MBSMM具有优越的滚动轴承故障诊断性能。

为了进一步验证所提方法的分类效果,笔者继续选取12种类型的滚动轴承状态数据进行验证。

滚动轴承参数及实验条件及参数设置如表2所示。

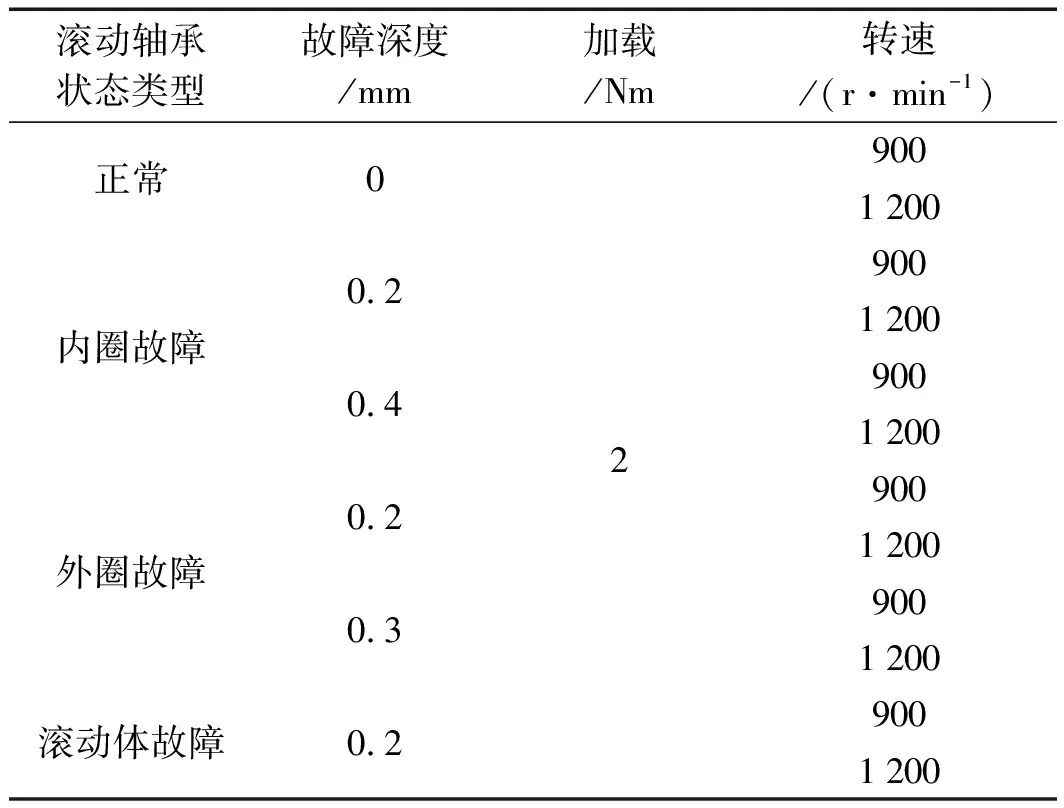
表2 实验条件及参数设置

笔者随机选取100个样本进行训练,100个样本作为测试。

经过测试样本分析,4种方法的识别率和对比结果如图3所示。

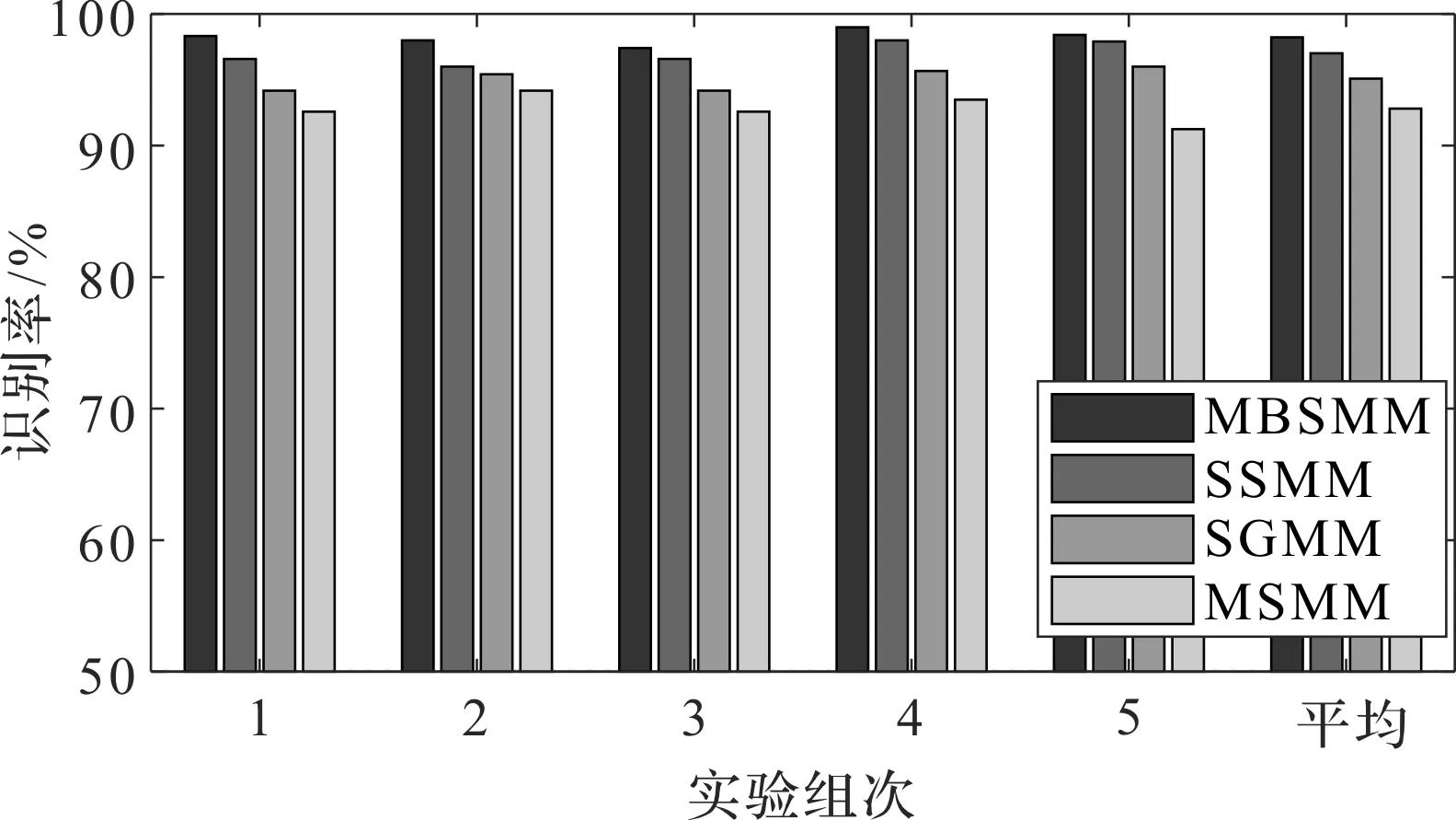
图3 4种分类方法的识别结果

从图3可以看出:MBSMM具有较高的识别率,平均识别率比SGMM高2%～5%,比MSMM高3%～8%,比SSMM高0.5%～3%。

为了全面验证所提出的方法,笔者引入kappa、准确率、召回率和F1得分,进行多角度比较分析[14]。

4种分类器在4种指标下的五次随机实验的结果,如表3所示。

由表3可以看出:笔者提出的MBSMM方法在各个指标上都具有优越的分类性能,并且优于其他分类方法。这是因为MBSMM采用所提方法,利用非平行边界超平面来隔离任意两种类型的数据,非平行边界超平面可以最大化任意两类样本之间的间隔。同时,与辛几何相似变换相结合,使模型具有鲁棒性,减弱噪声对分类结果的影响。

表3 4种分类器在4种指标下的对比结果

因此,MSMM、SSMM和SGMM在多分类、数据复杂的情况下,分类能力稍显不足。

3.3 统计指标分析

但是上述实验仅从各种判别指标来分析各种分类器的性能,并没有从统计理论上进行分析。因此,为了验证所提MBSMM方法是否比其他分类器有所改进,笔者使用Friedman检验(Friedman已经在其他统计检验中得到证明)来评估多分类器的性能[15]。

Friedman统计方法的表达式如下:

(11)

(12)

式中:N—分类类型数目;k—分类器个数;Rj—每个实验中第i个分类器的平均识别率排名。

为了获得可靠的统计结果,笔者采用正常、内圈故障、外圈故障和滚球故障的多种滚动轴承数据,进行了30次随机实验。

不同分类器的识别结果如表4所示。

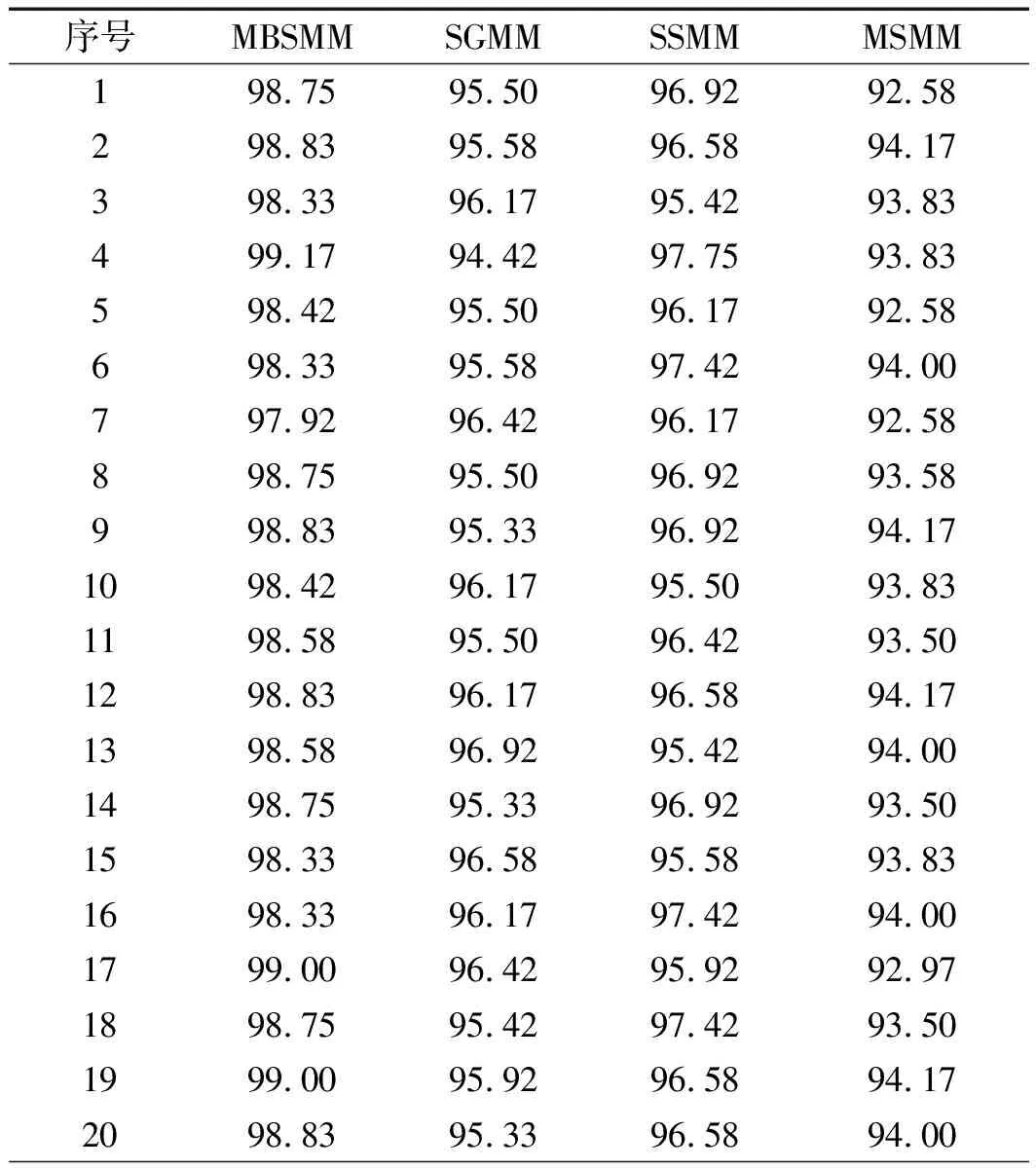
表4 不同分类器的识别率(%)

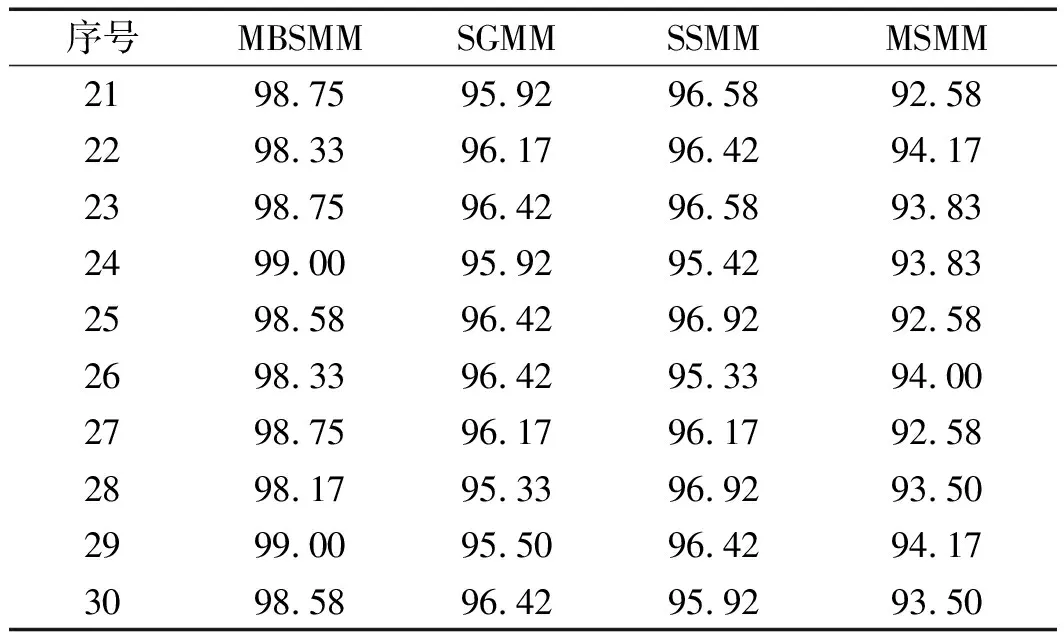
续表

从表4可以看出:MBSMM、SGMM、SSMM和MSMM的平均排名分别为1、2.666 7、2.3和4;当α=0.05,k=4,N=30时,F(4,30)的临界值为2.69。

(13)

式中:qα—Nemenyi试验的临界值。

根据Nemenyi测试表,qα=2.459 0。

MBSMM与其他3种分类方法的差值分别是(SGMM-MBSMM,2.666 7-1)、(SSMM-MBSMM,2.3-1)和(MSMM-MBSMM,4-1)。通过比较SGMM-MBSMM、SSMM-MBSMM、MSMM-MBSMM和CD=0.763 7,可以看出,MBSMM的分类性能明显优于SGMM、SSMM和MSMM方法。

综上所述,通过比较5种方法的识别率、时间、kappa、准确率、召回率和F1得分,以及统计检验,证明笔者提出的SRMM方法在整体性能上明显优于其他分类方法。

虽然其他方法也显示出优越的性能,但与SRMM方法相比,它们的性能明显不足。