基于自适应S速度轨迹的塔式起重机变幅定位与防摆控制研究*
2022-01-27宋鹏程
卢 宁,宋鹏程
(1.北京建筑大学 机电与车辆工程学院,北京 100032;2.北京市建筑安全监测工程技术研究中心,北京 100032)
0 引 言
塔式起重机(简称塔机)使用方便,具有高效的装卸能力,被广泛应用于生产建筑中[1]。
在塔机的作业过程中,吊物由于惯性作用易发生摆动,影响工作效率,同时易导致危险发生[2]。为防止吊物摆动,保证塔机上的小车定位精度,设计一种合理的控制策略十分必要[3]。
目前,针对起重机的定位防摆问题,学者们进行了大量研究,其中包括:(1)以角度、位移作为反馈量的闭环控制策略,例如模糊控制[4]、迭代学习控制[5]、神经元控制[6]、滑模控制[7]等;(2)以及无反馈量的开环控制策略,包括轨迹规划[8]、输入整形[9]等。
闭环控制中需增加传感器,对位移、摆角等反馈量进行获取,传感器性能对控制效果影响较大;开环控制方式对控制元器件性能要求低,常用于工程机械的控制中。因此,笔者选用开环控制方式对变幅运动进行研究。
随着计算机仿真技术发展,人们对工程要求不断提高。火箭军工程大学的刘春桐[10]利用MATLAB/Simulink、ADAMS建立了基于模糊PID控制的桥式起重机联合仿真模型,经仿真得到了结论,即模糊控制对吊物摆角的抑制效果较传统PID控制有明显提升。上海海事大学的吕锦超[11]通过MATLAB/Simulink与ADAMS联合仿真的方式,验证了双PID控制对于小车定位防摇具有良好控制效果。
上述研究以起重机的数学模型为依据,通过控制小车的驱动力,完成对小车定位及吊物防摆的控制,忽略了电机回路状态、控制系统参数等因素对驱动力输出的影响[12]。
因此,考虑到轨道摩擦力[13]等非线性因素,笔者将变频器、异步电机以及变幅传动系统加入考虑范围,提出一种基于自适应七段式S速度轨迹的控制策略,将小车的运动过程分为加加速、匀加速、减加速、匀速、加减速、匀减速、减减速七段速度轨迹,并对不同工况下的小车变幅过程进行机电联合仿真。
1 定位及防摆数学模型
为了寻找影响塔机吊物摆角的因素,笔者做了以下假设:(1)把吊物视作质点;(2)忽略钢丝绳的质量和形变;(3)忽略空气阻力影响。
小车在水平方向驱动力F的影响下沿X轴正方向移动,其运动关系如图1所示。
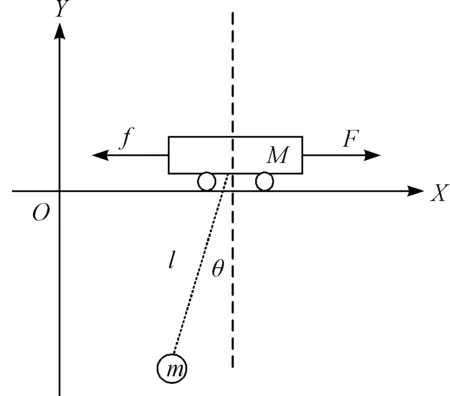
图1 变幅运动示意图M—小车质量;m—吊物质量;l—钢丝绳长度;X—小车定位距离;f—小车与轨道的摩擦力;θ—吊物与Y轴的夹角
根据Lagrange动力学方程[14,15],笔者以小车运动的初始状态建立其数学模型:
(1)
在防摆过程中,由于吊钩角度变化逐渐趋于0°,笔者在平衡点附近对其进行线性化,令sinθ=0,cosθ=1,又因:
(2)
所以,式(1)可化简为:
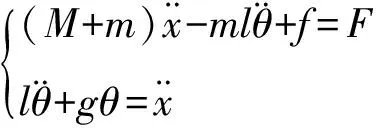
(3)
对式(3)进行变形可得:

(4)
同时:
a=d2x/dt2
(5)
式中:a—小车的加速度。
由式(4,5)可知:当确定了吊物的质量以及钢丝绳长度后,小车的加速度成为影响小车位移以及吊物摆角的关键因素。因此,需要合适的控制方法对小车的加速度进行控制,来实现定位与防摆的控制目标。
考虑到异步电动机的复杂特性,通过控制电动机的输出力矩,来控制小车加速度的方式较难实现[16]。因此,笔者选用速度控制方式,以电机转速作为输入量,对小车加速度进行控制。
2 自适应S轨迹算法
2.1 传统七段式S轨迹理论
目前常用的速度规划算法包括直线加减速、指数加减速、梯形(匀加速,匀速,匀减速)、S形以及多项式加减速[17]等。
考虑到塔机变幅驱动电机的机械特性与吊物的防摆效果,只有梯形、S形、多项式加减速算法适用于塔机的速度规划。其中:(1)梯形加减速算法,加速度曲线不连续,加速度突变对吊物摆角影响较大;(2)多项式加减速算法复杂,对工作元件的性能要求极高,难以应用在塔机变幅运动中;(3)S形轨迹平稳性高,且加速度曲线无突变,对吊重摆角影响较小。因此,笔者选取S形速度轨迹算法进行控制。
基于S形轨迹理论,将小车整个变幅过程分为7段,包括加加速、匀加速、减加速、匀速、加减速、匀减速、减减速。考虑到塔机变幅机构对速度和加速度的限制性要求,此处规定小车运动速度不超过变幅运动的最大速度Vmax,加速度不超过变幅运动的最大加速度amax;同时设加加速度为常量J。
对加加速度J规划如图2所示。

图2 加加速度规划图t—小车加加速度变化的时间节点;Jmax—加加速度的最大值
J与时间t(s)的关系如下:
(6)
塔机变幅运动中,小车的起始速度与终止速度都为0。根据变幅过程中吊物的摆动规律,必须保证加加速、减加速、加减速、减减速这4个时间段相等[18],则有:
t1-0=t3-t2=t5-t4=t7-t6
(7)
根据加加速度J值,规划加速度a如图3所示。
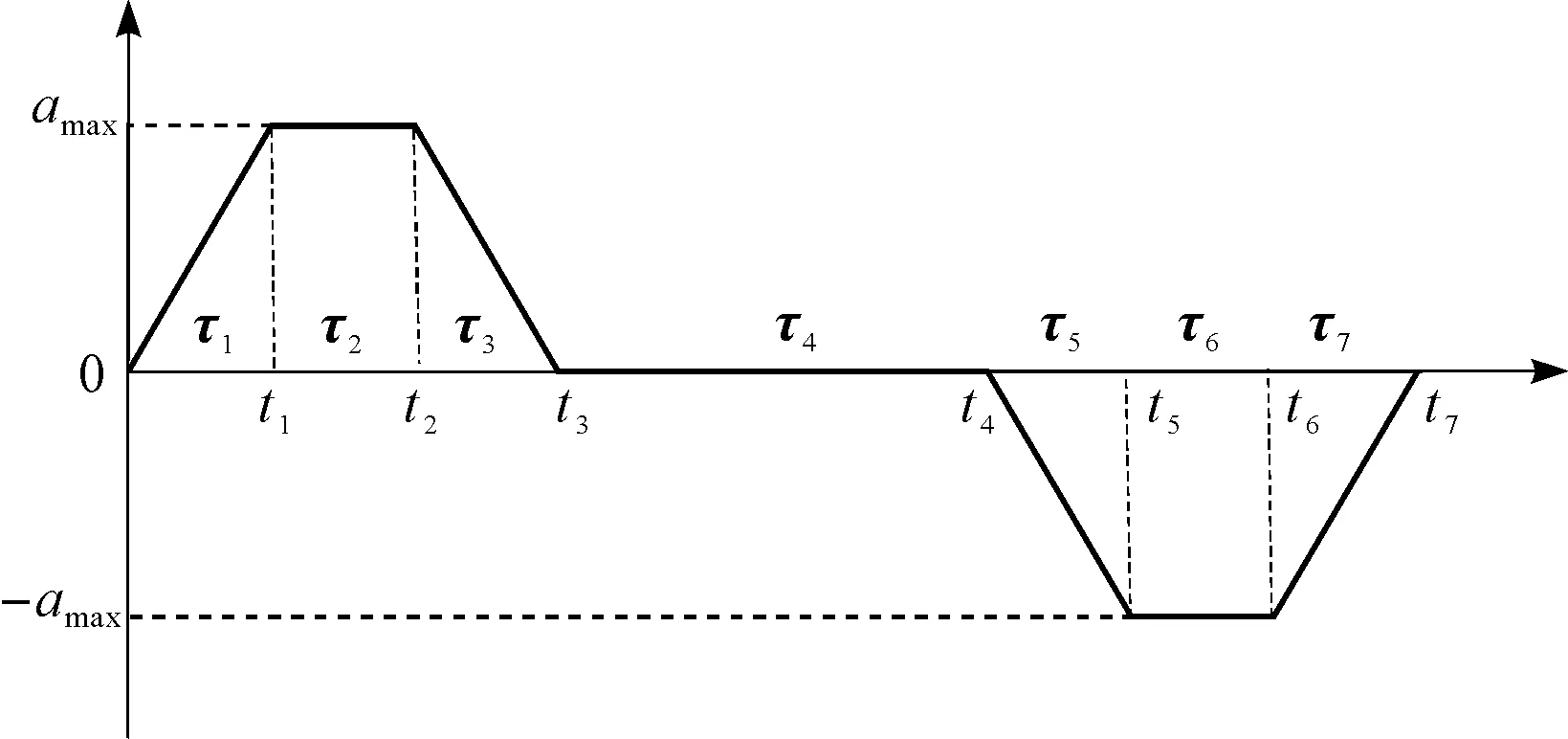
图3 加速度规划图τ—以当前时间节点出发的时间矢量;amax—加速度的最大值
加速度a与加加速度J、时间t(s)的关系如下:
(8)
其中:
amax=Jt1
(9)
由加速度曲线得到速度曲线如图4所示。
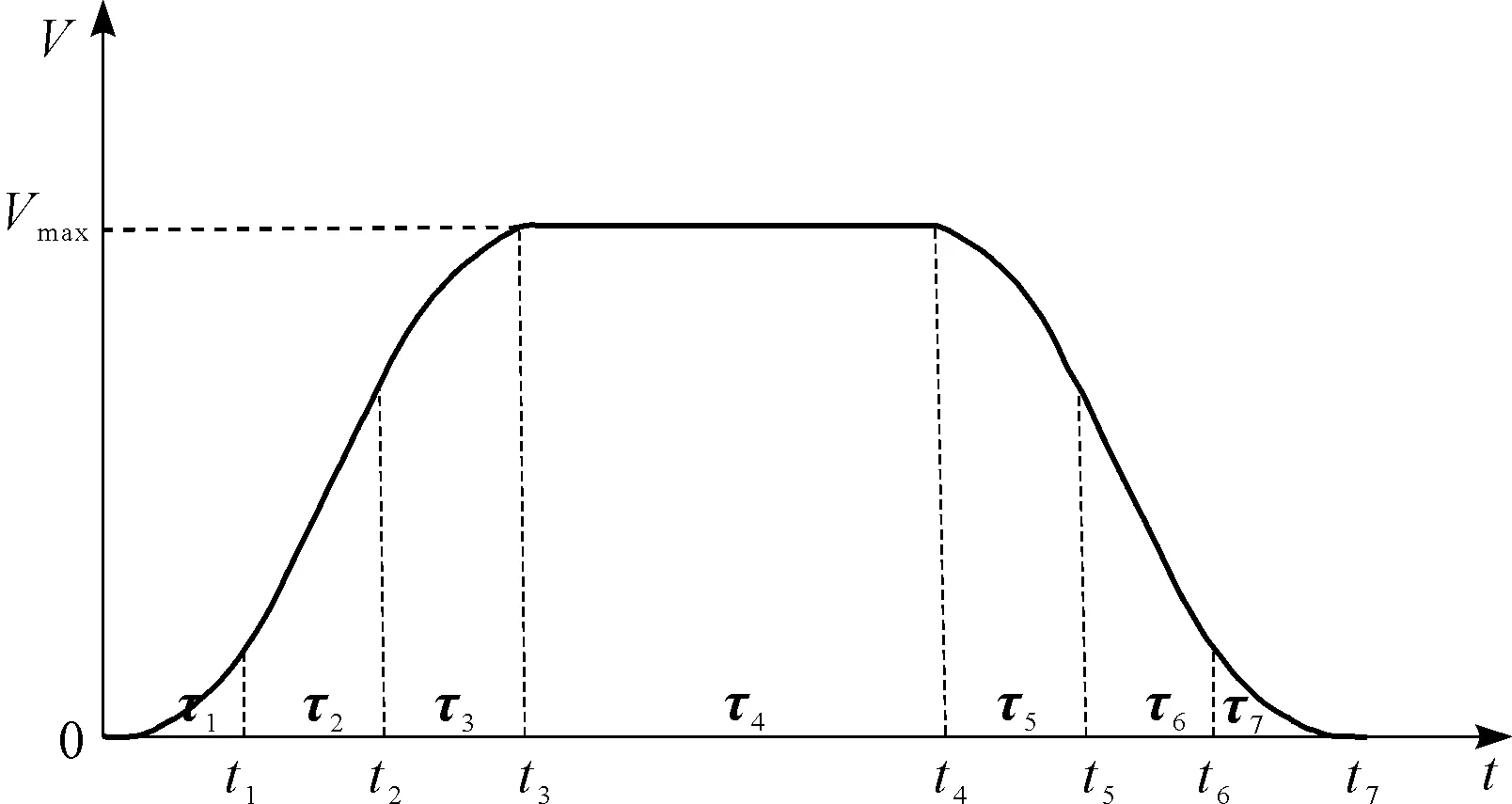
图4 速度曲线规划图Vmax—速度最大值
速度V与加速度a、时间t(s)的关系如下:
V(t)=
(10)
2.2 自适应S形轨迹算法
传统S形轨迹算法需要确定小车最大速度Vmax、最大加速度amax以及加加速度J。当加加速度选择不合适时,会造成加速度的突变,不利于吊物防摆;同时,在塔机定位防摆控制中,需对变幅小车进行点到点的轨迹规划。
因此,笔者在传统S形轨迹算法的基础上,提出自适应S形轨迹算法,即通过规定小车的目标位移距离值、限制速度和加速度的最大值,以及确定整体作业时间Tf,对小车变幅的速度轨迹进行规划。
基于自适应S形轨迹算法,可计算出小车的加加速度,即:
(11)
为减少加速度突变对摆角的影响,此处规定小车变幅运动必须具有匀加速段、匀速段以及匀减速段,由此得:
(12)
(13)
由于自适应S形轨迹算法计算量较大,在规定了前提条件以后,笔者采用MATLAB编写函数实现算法。
自适应算法流程如图5所示。

图5 自适应算法流程图
3 机电联合仿真平台
根据小车变幅系统的控制要求,笔者采用PLC、变频器以及三相异步电动机作为电气控制系统,通过减速器、卷筒以及钢丝绳等构成的传动系统对小车速度进行控制。
小车控制结构图如图6所示。

图6 小车控制结构图
3.1 矢量控制系统建模
由于异步电机的矢量控制理论发展成熟,且易于实现,笔者选取矢量控制方式,在Simulink中建立电机变频调速模型。由于异步电机系统复杂且耦合性强,建立其数学模型时需忽略空间谐波、磁路饱和、绕组电阻以及铁芯损耗的影响[19]。
笔者以转子磁链定向的方式建立电机矢量控制数学模型:
(1)电压方程:
(14)
(2)磁链方程:
(15)
(3)转矩方程和运动方程:
Te=npLm(isqird-isdirq)
(16)
(17)
当两相旋转坐标系按转子磁链定向时,有Φrd=Φr,Φrq=0,可得:
(18)
式中:Usd,Usq—定子等效绕组电压;Urd,Urq—转子等效绕组电压;wdqs,wdqr—定、转子相对角速度;Rs,Rr—定、转子绕组电阻;Φsd,Φsq—定子磁链;Φrd,Φrq—转子磁链;Lm—定、转子等效绕组互感;Ls,Lr—定、转子等效绕组自感;isd,isq—定子等效绕组电流;ird,irq—转子等效绕组电流;P—微分算子;Te—电磁转矩;np—电机极对数;TL—负载转矩;J—电机等效转动惯量;ω—电机转子的转速。
由式(18)可知,只需控制isq,便可对电磁转矩进行控制。
基于上述数学模型,为保证电机转速的跟踪性能,笔者选取通过电流滞环控制PWM逆变器的异步电机矢量控制方法(其转速环、电流环采取PI控制器)。
为验证控制策略的有效性,此处选用合适的电机参数,如表1所示。
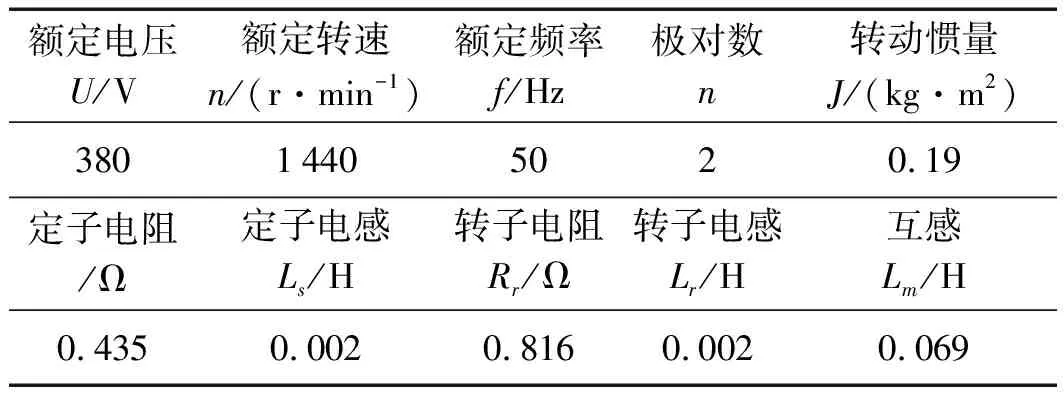
表1 电机参数表
3.2 系统动力学建模
塔机传动系统包括小车、滑轮、减速器与钢丝绳等。笔者在SolidWorks软件中建立塔机变幅机构的实体模型,并将其导入ADAMS中。
在变幅运动中,由于钢丝绳柔性的特点,难以建立较精确的非线性动力学模型。因此,笔者使用ADAMS/Cable模块建立钢丝绳系统[20],并依据工程经验,在Cable模块中设置钢丝绳参数,并确定滑轮和锚点的具体位置[21](其中,吊钩处连接滑轮为动滑轮,小车处连接滑轮为定滑轮)。
笔者在ADAMS中为模型添加部件约束以及运动副,如表2所示。

表2 约束/运动副设置表
在ADAMS中,变幅机构动力学模型如图7所示。

图7 变幅机构动力学模型
在ADAMS中,钢丝绳和滑轮的缠绕方式局部放大图如图8所示。
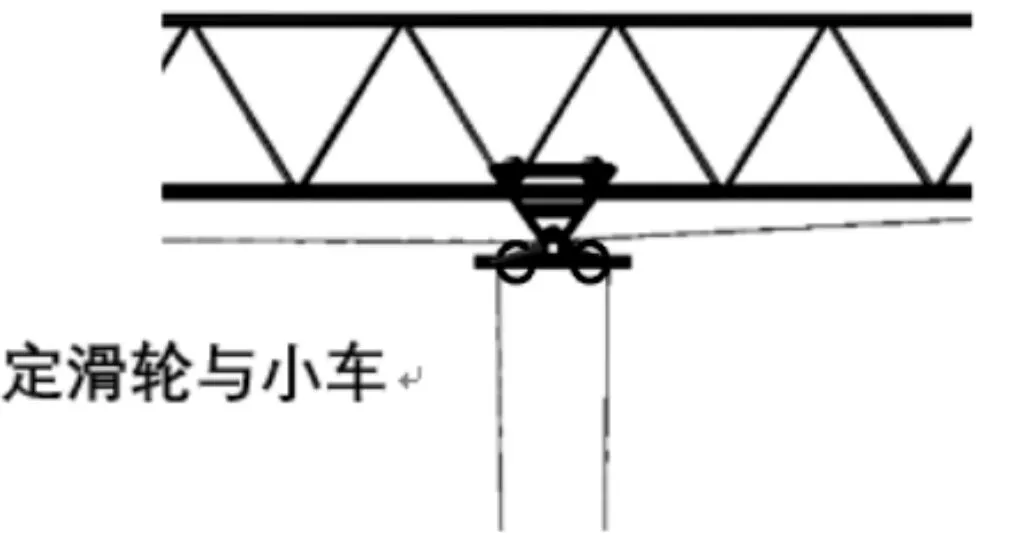
图8 小车局部放大图
3.3 联合仿真平台搭建
笔者利用自适应S形轨迹算法,对变幅小车的速度进行控制,取减速比为24,对小车的最大加速度与最大速度进行限制;确定ADAMS模型的输入状态变量为小车速度V,输出状态变量为小车位移S,吊钩角度为θ;利用ADAMS/Controls接口将模型导入Simulink中进行联合仿真。
机电联合仿真过程如图9所示。

图9 机电联合仿真图
4 仿真分析
4.1 不同速度轨迹对比研究
考虑到算法的适用性,此处选取梯形轨迹与S形轨迹进行对比研究。笔者分别选取工况一:绳长20 m,变幅距离20 m,起重量0.5 t;工况二:绳长30 m,变幅距离30 m,起重量1 t进行仿真。
此处设定小车最大速度不超过1.2 m/s,最大加速度不超过2 m/s2,仿真时间为40 s。
仿真结果如图(10~13)所示。

图10 工况一小车位移图

图11 工况一小车摆角图
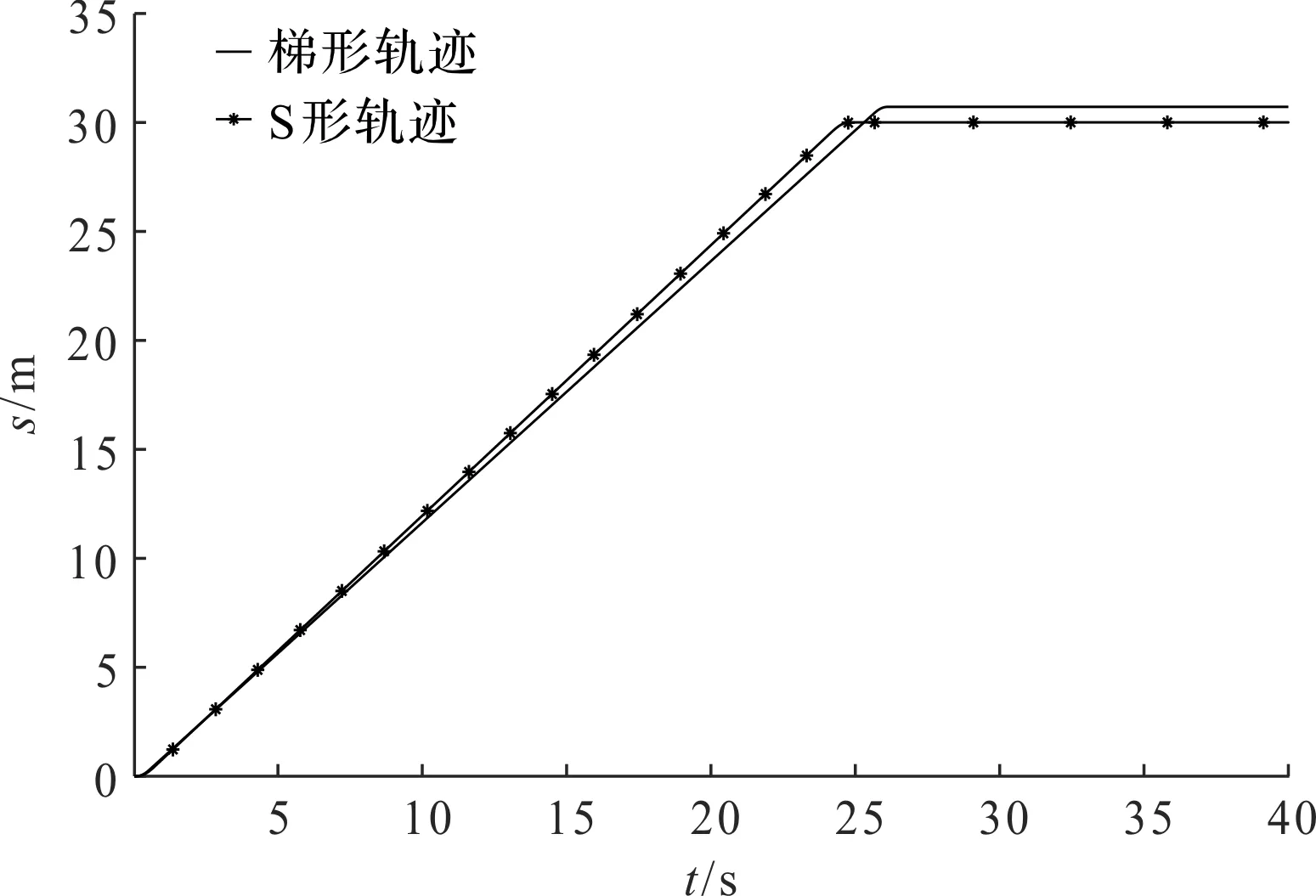
图12 工况二小车位移图

图13 工况二小车摆角图
由图(10,12)可知:两种轨迹下,小车均能到达指定位置附近,且S形轨迹算法定位更精确;
由图(11,13)可知:小车停止后,吊物由于自身惯性以及重力的影响,仍将处于摇摆状态;梯形轨迹下,吊物摆角的最大幅值为6.5°,S形轨迹将摆角幅值限制在了5°以内,较梯形轨迹减小了23%,可以更好地符合作业安全性要求。该结果证明,S形轨迹较梯形轨迹有更好的防摇性能。
4.2 不同工况对比研究
笔者采取控制变量法,取不同绳长(l)、吊物重量(g)以及变幅距离(s)的工况进行仿真。同样,此处限制小车的最大速度、最大加速度,取仿真时间为40 s。
仿真工况如表3所示。

表3 仿真工况表
仿真结果如图(14~19)所示。
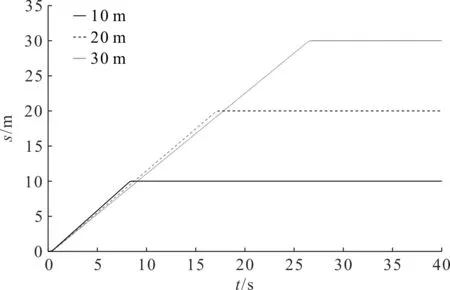
图14 不同变幅距离小车位移图
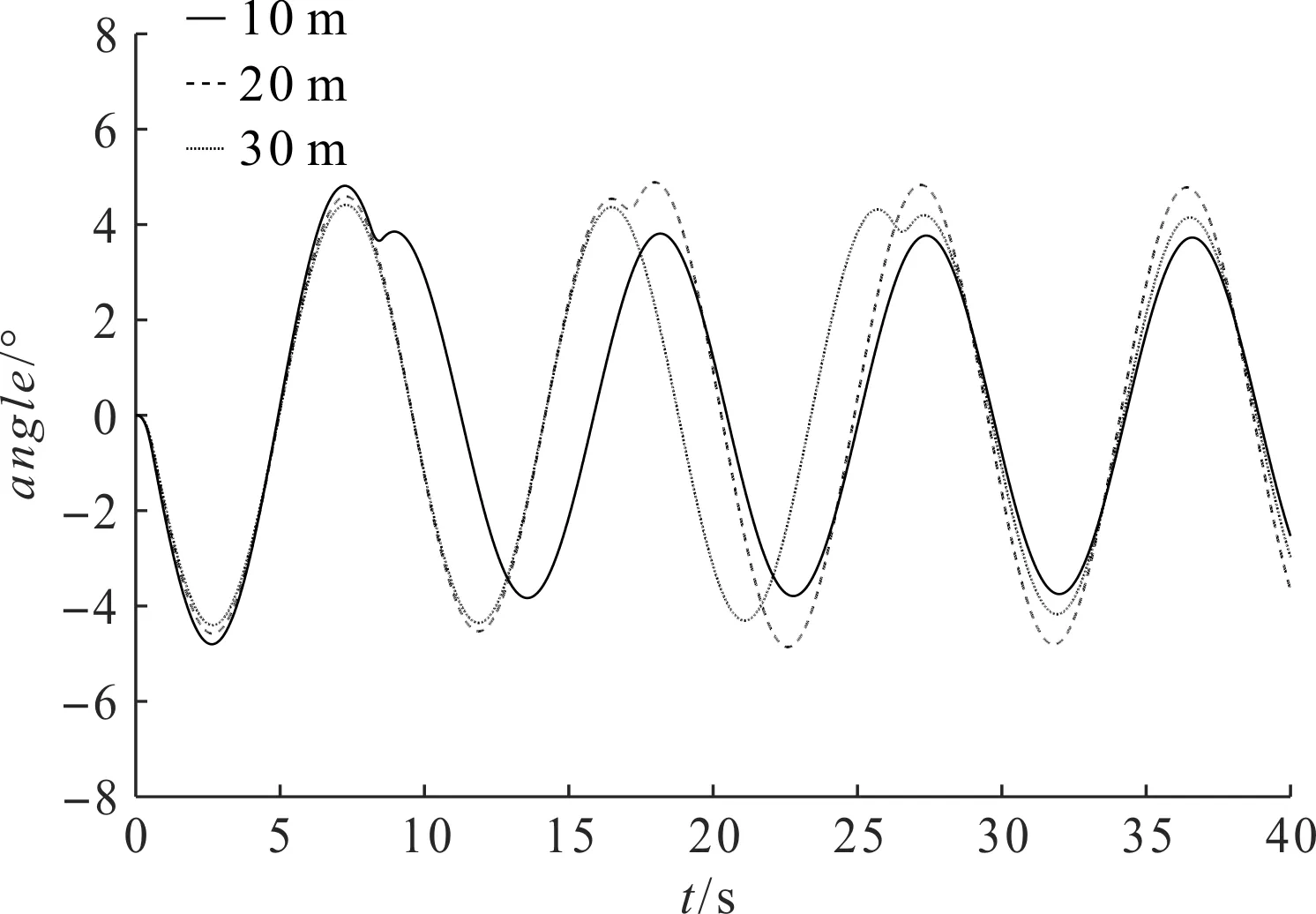
图15 不同变幅距离小车摆角图
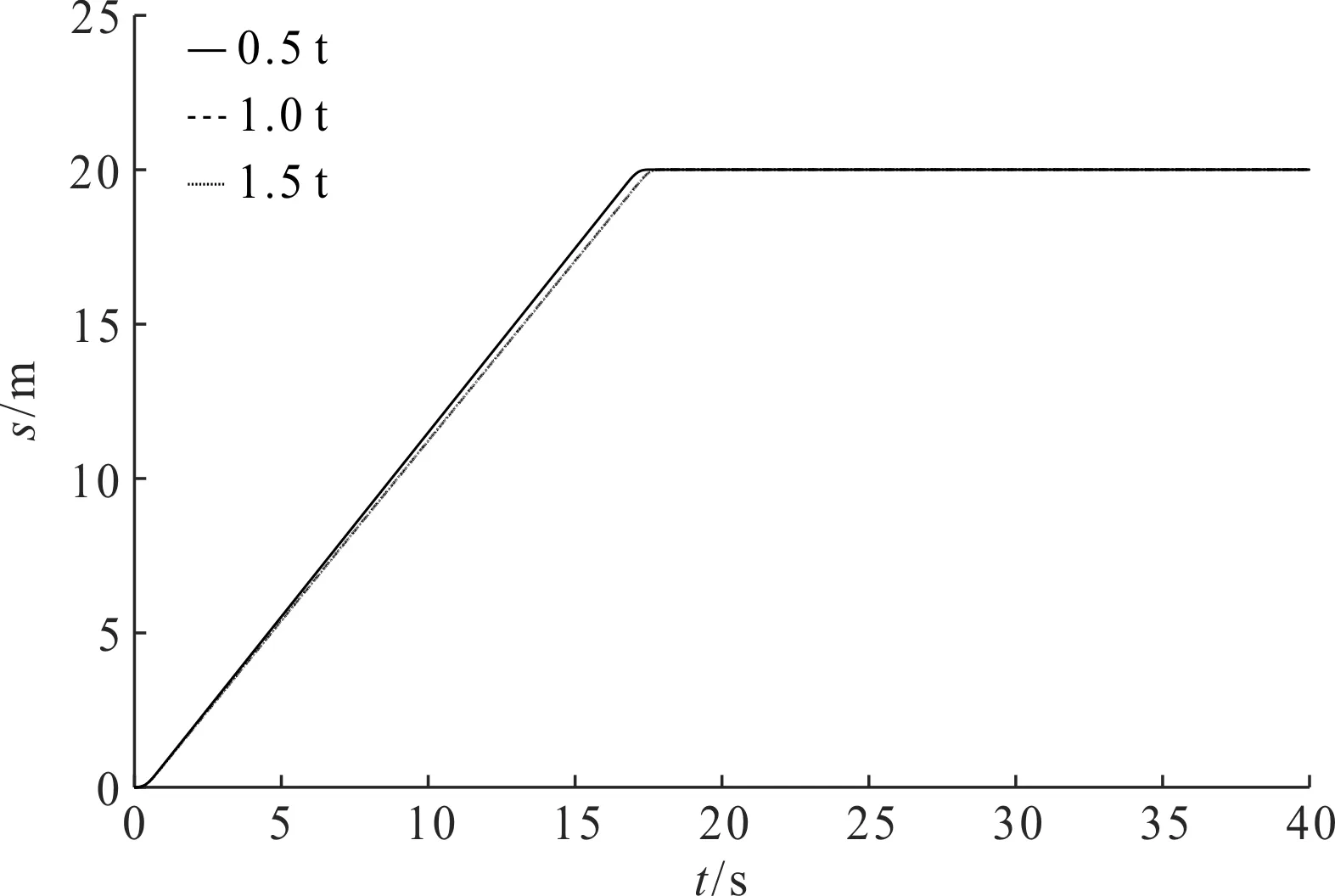
图16 不同吊物重小车位移图

图17 不同吊物重小车摆角图
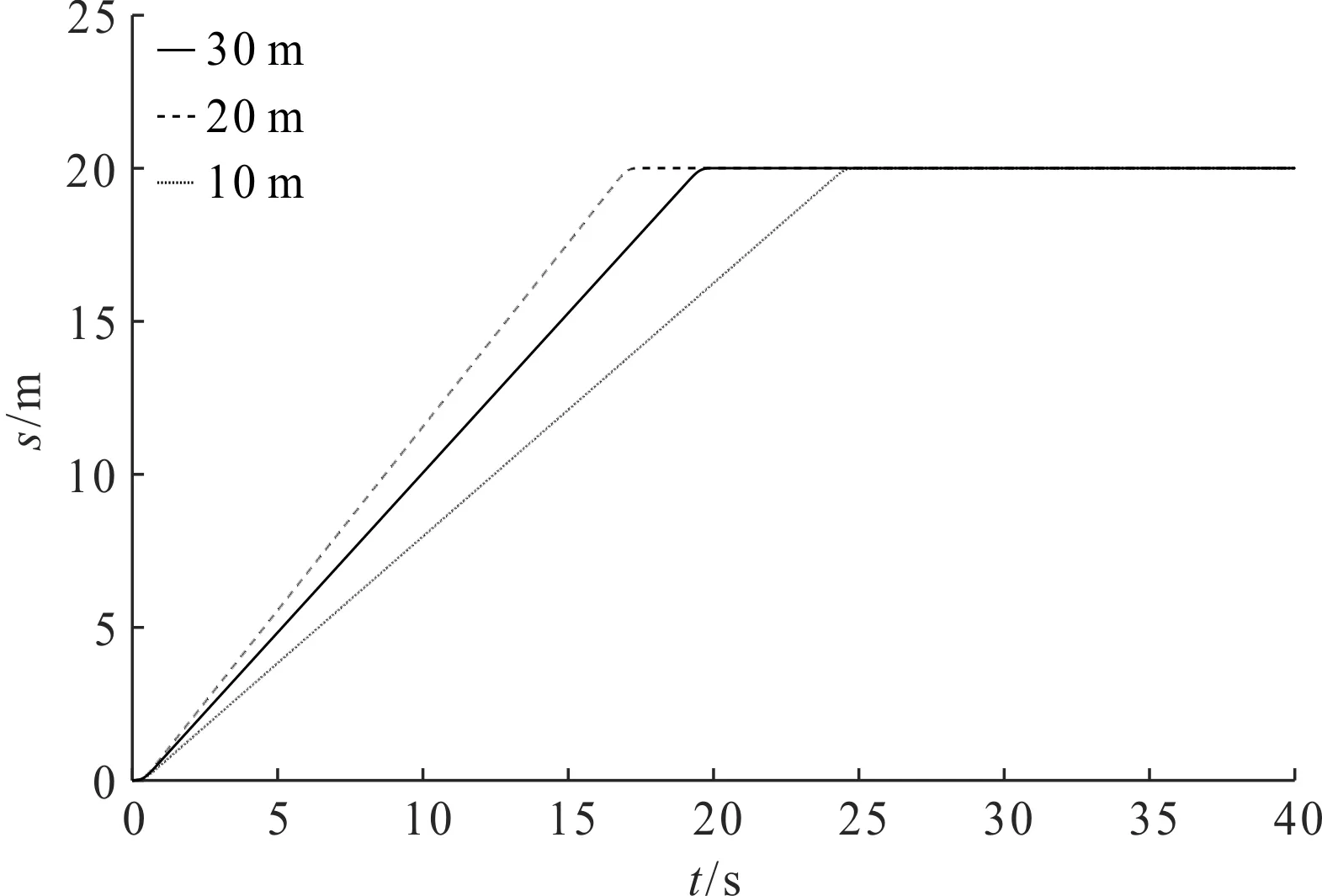
图18 不同绳长小车位移图

图19 不同绳长小车摆角图
综合分析图(14~17)可知:在变幅距离不同和吊物重量不同的工况下,小车均能到达指定位置附近;且在S形轨迹的规划下,吊物摆角都能被限制在5°左右,符合塔机作业的安全性要求。
分析图(18,19)可知:在不同绳长工况下,采用S形轨迹虽能达到小车定位与吊物防摆的要求,但由于S形轨迹算法中对吊物防摆要求的限制,小车到达指定位置的时间不同,影响了作业效率。
因此,在实际作业中,为兼顾作业效率与安全性,应选择合适的起升距离。同时,观察图19仿真结果可知,吊物的摆动周期随着绳长的增加而增大,这与文献[22]的结论相吻合。
5 结束语
为防止塔式起重机变幅作业过程中,由于吊物的摆动造成危险,笔者利用Lagrange方程找出影响塔机吊物摆动的因素,提出了一种自适应S形速度轨迹算法,来解决小车的定位和吊物的防摆问题,并建立了基于PI控制的塔机变幅机构机-电联合仿真模型,对该控制策略进行了验证。
研究结果表明:
(1)S形速度轨迹的定位防摆效果优于梯形轨迹;
(2)S形速度轨迹对于变幅运动的多种工况都具有良好的定位效果,且都能将吊物摆角限制在5°左右;
(3)钢丝绳长度影响吊物的摆动周期,且两者呈正相关性。
此外,为了更好地研究钢丝绳长度变化对吊物摆动的影响,在后续的研究工作中,笔者将起升运动与变幅运动进行耦合考虑,并综合分析该控制策略的防摆性能。
