600 km/h高速磁浮列车明线交会横向气动性能

杨永刚， 陈大伟， 梅元贵

(1. 兰州交通大学 甘肃省轨道交通力学应用工程实验室， 兰州 730070；2. 中车青岛四方机车车辆股份有限公司， 山东 青岛 266111)

磁浮列车明线高速交会时，侧向气动力、侧滚力矩和偏航力矩发生剧烈波动。明线交会产生巨大的瞬态压力冲击对列车侧窗和车体强度均会带来严重影响，交会压力波严重时会导致车窗玻璃破碎的危险。横向气动力和侧滚力矩的急剧变化，会导致车体横向摆动和侧翻、倾斜，严重时会导致车体底部设施和线路设施发生损坏；偏航力矩的剧烈变化会引起列车的“蛇行运动”[1-5]，这种现象随交会速度的增加而更加严重。我国时速600公里高速磁浮列车设计运行速度为600 km/h，是目前高速列车中设计运行速度最高的，明线交会时，底部气流横向流动受到T型轨限制，侧向气动力波动更加剧烈，引起车体发生横向摆动和侧滚运动[6]，最终导致悬浮间隙发生变化[7-8]，严重时引起车体与轨道梁产生磨损，最终危及行车安全。因此，必须对我国600 km/h高速磁浮列车明线交会横向气动性能进行深入研究。由于目前对列车交会过程中的气动作用力很难通过实车试验和动模型缩尺实验直接测量，目前的间接测量方法要准确获得交会过程中的气动力有一定困难[1]，基于此，对我国600 km/h高速磁浮列车横向气动性能的数值模拟研究是亟需的。

国内外对于高速磁浮列车明线交会气动性能的研究，主要是针对我国上海磁浮和日本磁浮。Suzuki等[9]对日本山梨线MLX01列车在明线高速交会时，侧向力和侧滚力矩的变化特性，以及横向摆动位移做了相关研究，为磁浮列车悬浮间隙、电磁力设置提供了试验数据。对于我国上海磁浮，做了大量的明线交会空气动力学性能试验，为后续研究我国TR08磁浮列车相关空气动力学问题提供了实车试验数据和依据[10-11]。毕海权等[11-12]对上海磁浮列车明线以相对速度860 km/h和1 000 km/h交会时的压力波进行数值模拟，发现明线高速交会时，车体发生大的横向振动，结果为进一步研究磁浮列车运行安全、舒适度等动力学性能奠定了基础。梁习锋等[13]对横风作用下，磁浮列车明线交会时的横向气动性能进行数值模拟研究，为后续研究磁浮列车在大风环境下的运行安全性提供可靠数据。Huang等[14]采用三维数值模拟方法，研究了上海磁浮列车以430 km/h在明线等速交会时列车表面压力和列车风，给出了站台安全距离，为磁浮列车站台设置、以及通过站台速度提供理论依据。陈敬旭[15]采用三维数值模拟方法，对比了新型磁浮列车和TR08列车明线交会时的横向气动性能，新型列车的气动性能明显优于TR08列车，为磁浮列车气动外形设计提供参考。刘堂红等[16-18]以减缓明线交会压力波为目标，对我国磁浮列车进行气动外形优化，推荐出气动性能较优的列车外形，其气动性能明显优于TR08磁浮列车，为磁浮列车外形设计提供参考依据。由于日本山梨线车辆在“U”型导轨槽中运行，而600 km/h磁浮车辆环抱“T”型导轨运行，轨道结构完全不一样，明线交会时，列车横向气动性能相差很大。上海磁浮列车明线的最高运行速度为430 km/h，与600 km/h磁浮列车速度相差较大，而且TR08和600 km/h列车的气动外形有明显差异，特别是曲线头部长度，导致气动性能相差很大。因此，上海磁浮和日本磁浮气动性能的前期研究，为600 km/h磁浮列车提供数据参考时存在局限性，有必要对我国600 km/h磁浮列车的气动性能进行研究。

本文采用三维数值模拟方法，对我国600 km/h高速磁浮列车明线交会横向气动性能进行数值模拟研究，探讨了明线交会压力波和气动力的变化原因和变化规律，以及车速的影响特性。为600 km/h磁浮列车电磁力、悬浮间隙、线间距和各方向阻尼等设置提供基础数据；最后通过分析流场特性，为局部外形气动优化提供参考；为今后进一步研究列车运行安全、舒适度等动力学性能奠定基础。

1 计算模型

磁浮列车以600 km/h运行时，马赫数为0.49，当马赫数大于0.3时，空气流动为可压缩流动，因此，磁浮列车明线运动时，列车周围的流场为可压缩流动。RANS下的k-ωSST湍流模型在列车空气动力学中有广泛应用[19-21]。采用STAR-CCM+软件和k-ωSST湍流模型，压力-速度耦合采用SIMPLE算法，对流项采用二阶迎风格式，时间离散采用二阶隐式格式，速度、压力求解采用AMG线性求解器。非定常时间步取0.001 2 s，每个求解步含内迭代20次。壁面处理采用全y+方法。列车运动通过STAR-CCM+软件中重叠网格方法[22]实现。

1.1 列车和轨道模型

根据列车设计运行时的实际编组情况，列车计算模型采用5编组全尺寸600 km/h高速磁浮列车模型。取列车悬浮架最底部到车顶最高位置的距离为车高，车高4.20 m，头尾车长28.08 m，鼻长16.5 m，中间车长24.52 m，5编组列车全长130 m，车宽3.70 m。列车计算模型忽略了车体外部的复杂细节，保留了风挡、滑橇等关键结构，几乎还原了真实的磁浮列车外形结构，其空气动力学外形如图1和图2所示。

图1 磁浮列车气动外形(m)Fig.1 Maglev train model(m)

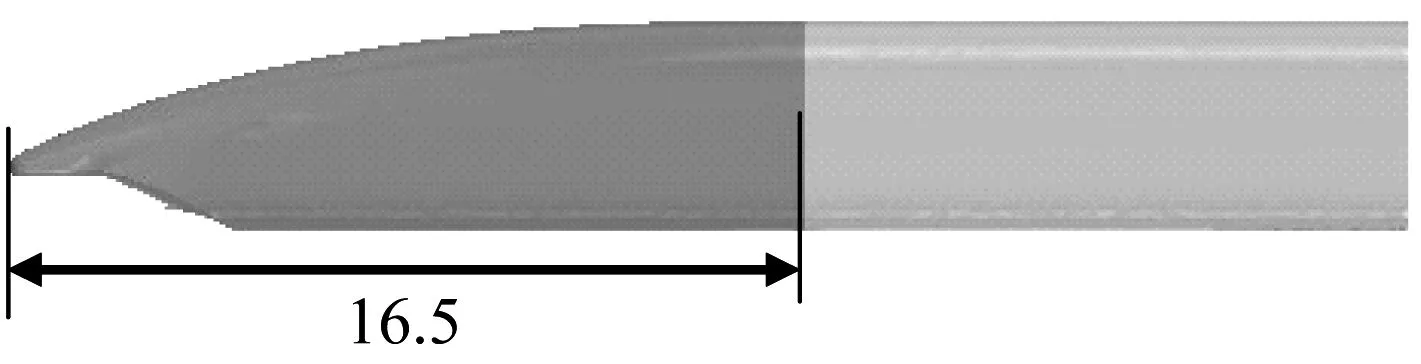
图2 头尾车流线段(m)Fig.2 Stream line zone(m)

轨道梁采用600 km/h高速磁浮列车的T型轨道梁，轨道梁高1.25 m，轨道梁上表面宽2.8 m，下表面宽1.94 m，横截面积为2.19 m2，线间距5.6 m，如图3所示。为准确模拟轨道梁周围的流场特性，轨道梁尽量保持真实几何外形。

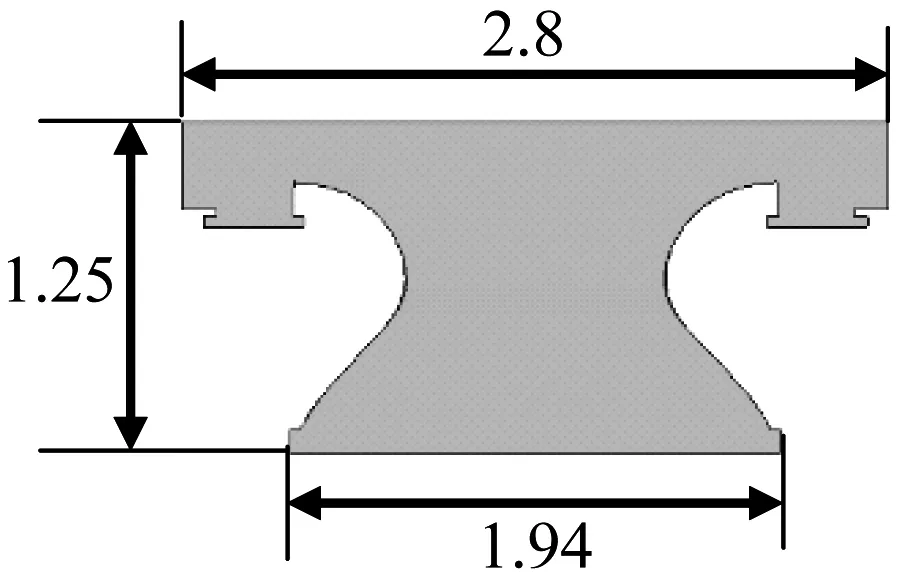
图3 T型轨道梁几何模型(m)Fig.3 T Type track model(m)

根据CEN标准[23]，压力系数、侧向力系数、侧滚力矩和偏航力矩系数定义如下

压力系数：

(1)

侧向力系数：

(2)

侧滚力矩系数：

(3)

偏航力矩系数：

(4)

式中，ρ为空气密度，取值1.225 kg/m3；v为列车运行速度；S为参考面积，取值12.0 m2；F为横向气动力；Mx是对纵向轴线x轴取矩，h取列车轨面以上高度3.3 m；Mz是对z轴取矩，l取一半车厢长度12.26 m。

1.2 计算区域

计算区域如图4所示，计算域长1 600 m，高200 m，宽400 m，交会前，两车车头鼻尖相距1 040 m。

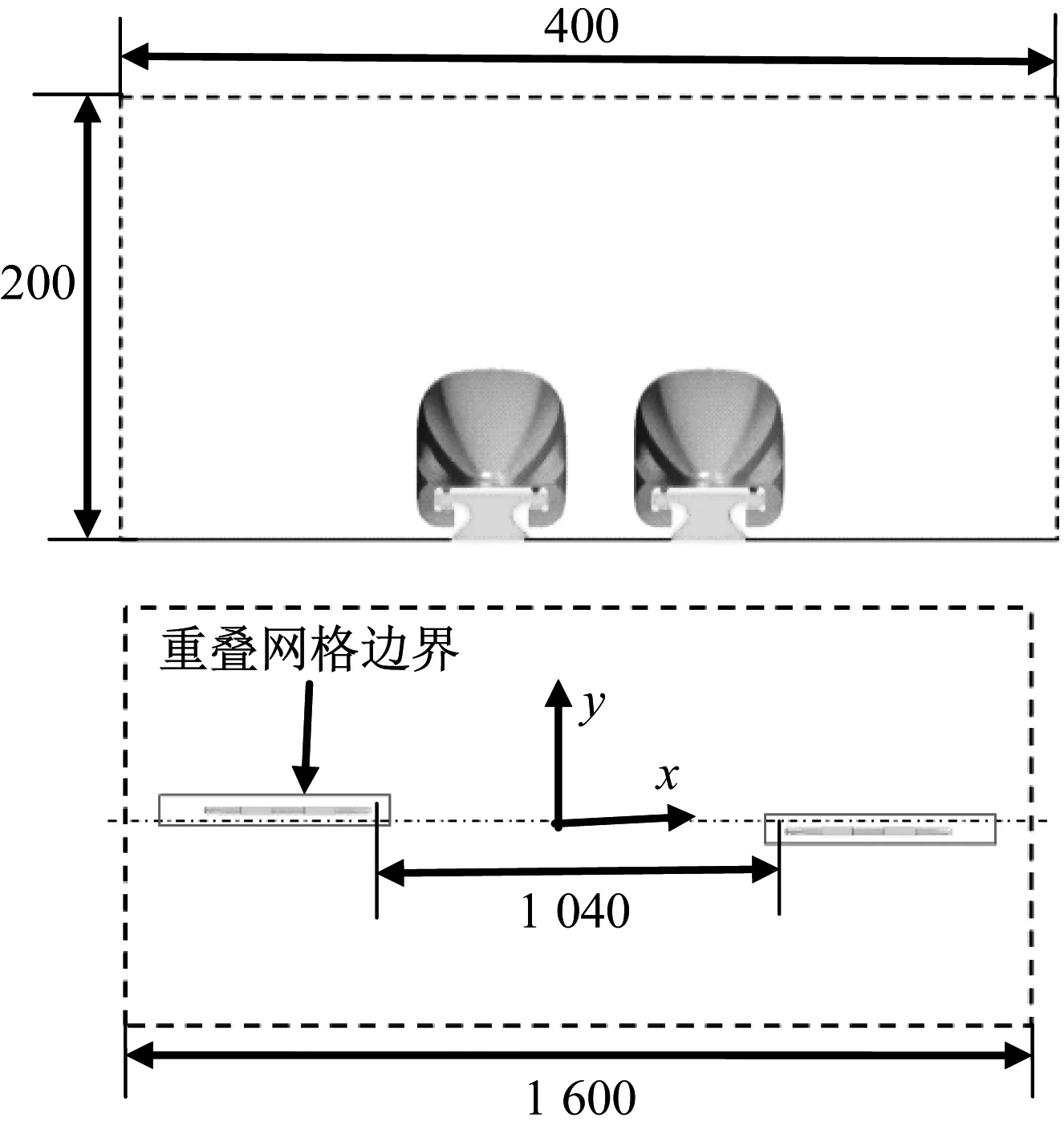
图4 计算区域示意图(m)Fig.4 Computational domain(m)

图5给出了计算域边界类型，列车表面、轨道梁表面和路基表面为无滑移固体壁面，其切向速度都设定为0。外开阔空间的各表面为自由流边界，用于模拟无穷远处的可压缩流动，它使用黎曼不变量来确定边界处的流动变量。

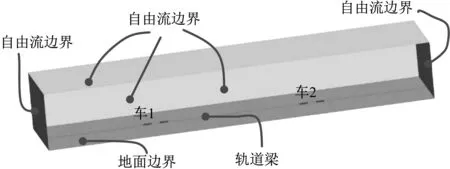
图5 边界条件示意图Fig.5 Boundary conditions

1.3 初始条件

计算对应的空气参数按照海平面国际标准大气(ISA)给定。在t=0时刻，列车和周围流场均静止，各处压力等于参考压力，即标准大气压；湍流物理量也处处为零，温度为288 K。在求解过程中，为了避免出现非正常物理量波动[24-25]，采用光滑启动技术，即列车由静止逐渐加速至实际运行速度，列车光滑启动距离为300 m。

1.4 网格划分

车头和车尾处流场变量梯度很大，对车头迎风区和车尾尾流区局部加密。在列车底部、滑撬和风挡附近流场变化剧烈且容易形成漩涡流动，对这些区域单独加密；列车底部和轨道梁间的垂向间隙很小，垂向方向流场变化复杂、剧烈，采用各项异性加密块进行垂向加密。列车附近到计算区域远场空间，流场变化逐渐减小，列车附近到远场区域采用网格逐渐由密变疏、均匀过渡的网格密度控制方法。在车体表面和轨道梁表面设置10层边界层，y+取30，近壁面第一层网格厚度为0.264 mm，拉伸比1.2。通过对计算后的流场加以检验性计算，最终划分出合理的网格。计算模型采用Trim网格和Prism网格，网格总数6 000万，如图6所示。

1.5 压力测点布置和力方向定义

为了研究车体表面的压力变化特性，以及交会侧压力与横向气动力的相互关系，在列车运行方向上，每节车厢的中间横截面处布置如图7(a)所示测点，其中，测点1位于交会侧。将沿y轴正方向的横向气动力定义为正侧向力，负方向的为负侧向力。磁浮列车悬浮在轨道梁上，与轨道梁没有直接接触，明线交会时，列车沿纵向对称面来回侧翻，而且列车向内侧翻和向外侧翻幅度相当，因此将侧滚力矩的轴取在车体纵向对称面和轨平面的交线，更符合实际情况。每节车厢偏航力矩的取矩点定在每节车厢的几何中心位置。坐标轴和气动力方向如图7(b)所示。z方向的零点为轨平面位置。

(a) 曲线头部网格

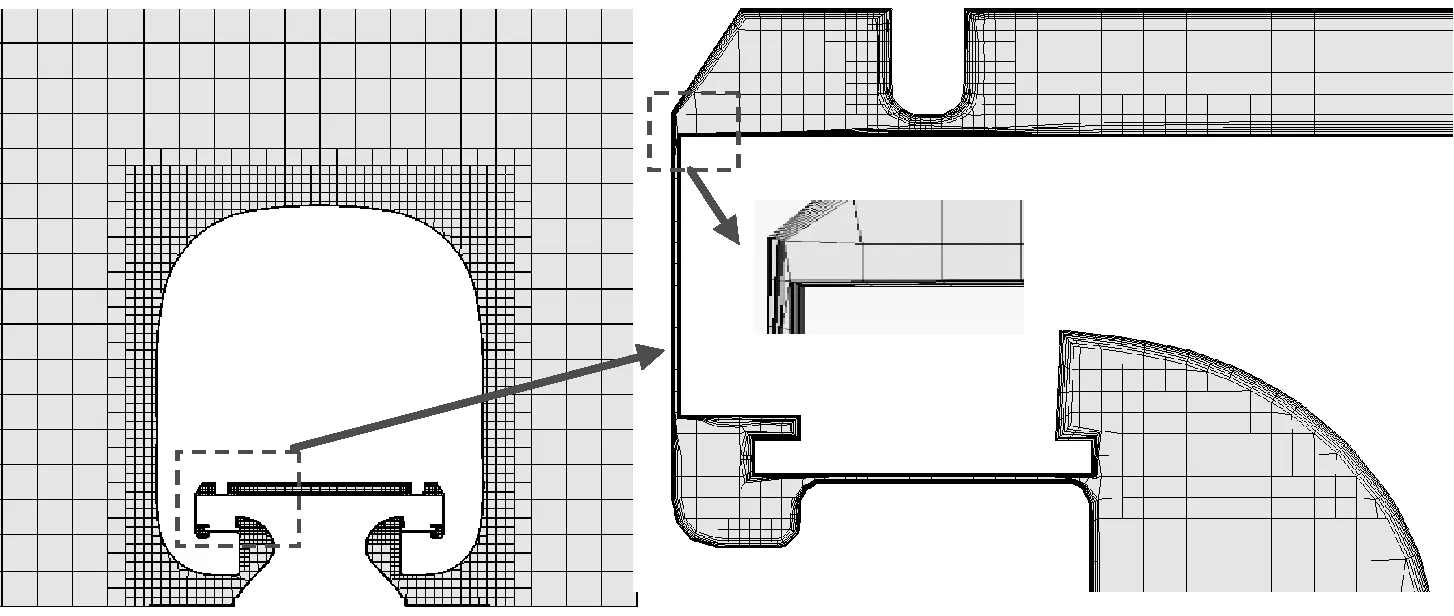
(b) 车身截面网格

(c) 车体表面网格图6 网格展示图Fig.6 Computational mesh

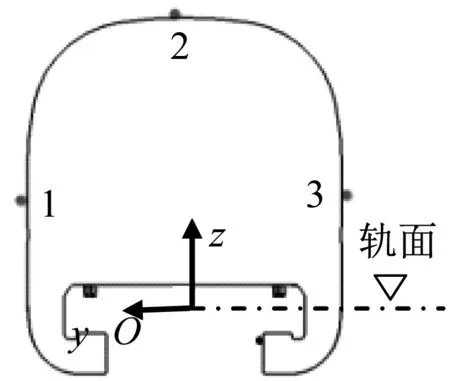
(a) 测点布置图

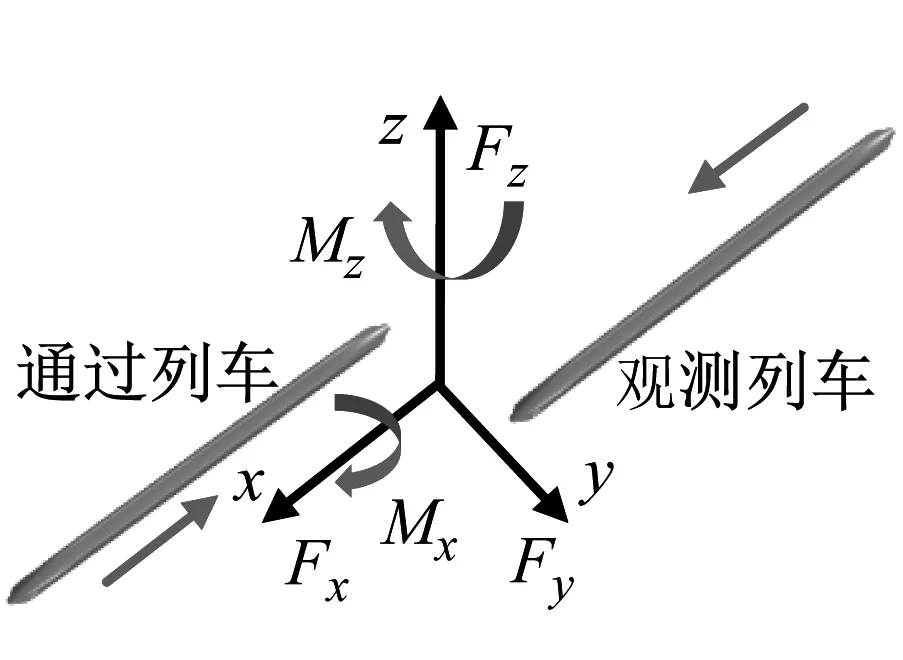
(b) 坐标轴示意图图7 测点布置和坐标轴示意图Fig.7 Monitoring points and axises

2 计算结果与分析

2.1 计算方法验证

2003年7月，我国在上海磁浮线，采用TR08列车进行了空气动力学实车试验。为了研究列车明线交会时，车体表面的压力变化特性，在交会侧车体表面布置压力监控点，如图8所示。实车试验所用的列车为：5编组(PV2)和2编组(PV3)，试验在PV3上进行。数值模拟验证中，列车模型、轨道和地面条件尽量保持与实车试验一样。对静止交会中(PV2速度为500 km/h，PV3静止)，P3监测点的压力进行对比，如图9所示，pmax为会车压力波最大正压值；pmin为会车压力波最大负压值。

由图9可知：实车试验与数值模拟的压力波动趋势基本吻合，压力峰值相差很小。表1统计了其压力波最值，交会压力波的最大正负压值误差分别为2.9%、7.1%。由于实车试验时存在很多干扰因素，如实际风速不可能为零、车身个别部件的突起等，因此计算结果有一定程度误差是合理的。TR08和600 km/h磁浮列车网格划分方法和网格尺度几乎完全一样，而且数值求解模型也完全一致。因此，采用TR08会车压力波来验证论文采用的计算方法和网格划分方法是有效的。因此，论文所采用的计算模型和计算方法有足够的精度，计算模型正确，可用于求解高速磁浮列车明线交会空气动力学问题。

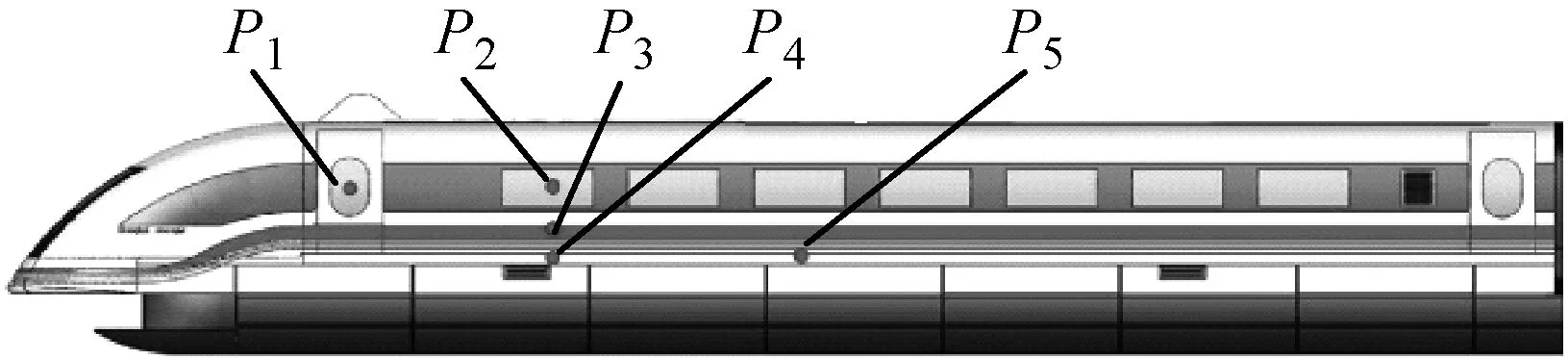
图8 压力传感器布置示意图Fig.8 Sensor placement and labels

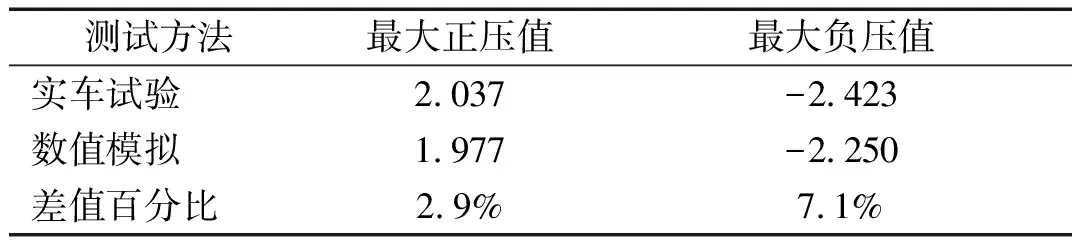
表1 P3点压力最值Tab.1 Pressure peak of P3

2.2 车体表面压力变化特性

以600 km/h明线等速交会为例，研究列车明线交会时的流场特性。图10给出了明线稳定运行时车体侧面(垂直于z轴，z=0.35 m处，图中黑色点划线位置，轨平面位置处z=0)的压力分布曲线，由于列车沿xOz平面对称，取一侧表面的压力进行分析，0位置为车头鼻尖点。由图可知：当列车在明线稳定运行时，头尾车流线区域的压力波动幅度很大，车头压力波动幅度大于车尾的波动幅度。在车头鼻尖位置，由于车头对周围空气的挤压形成高压区，在设备舱前端导流区域，车体侧面的负压较强，接近平直车身，压力逐渐恢复至零附近。从尾车流线段开始向车尾鼻尖，受空气绕流及分离流动的影响，车体侧面的压力从零附近开始减小，在设备舱导流区域处，车体侧面的压力减小到极小值；随后，压力开始快速增大，在车尾鼻尖处，增大到极大值。平直车身表面的压力接近于零，几乎没有压力波动，风挡处存在较大的压力波动。列车侧面这种压力分布特性，在明线交会时，会辐射到观测列车上，与观测列车侧面的压力叠加，引起剧烈的压力波动，最终导致列车受到大幅波动的侧向力作用，引发车体产生横向摆动和侧翻运动。

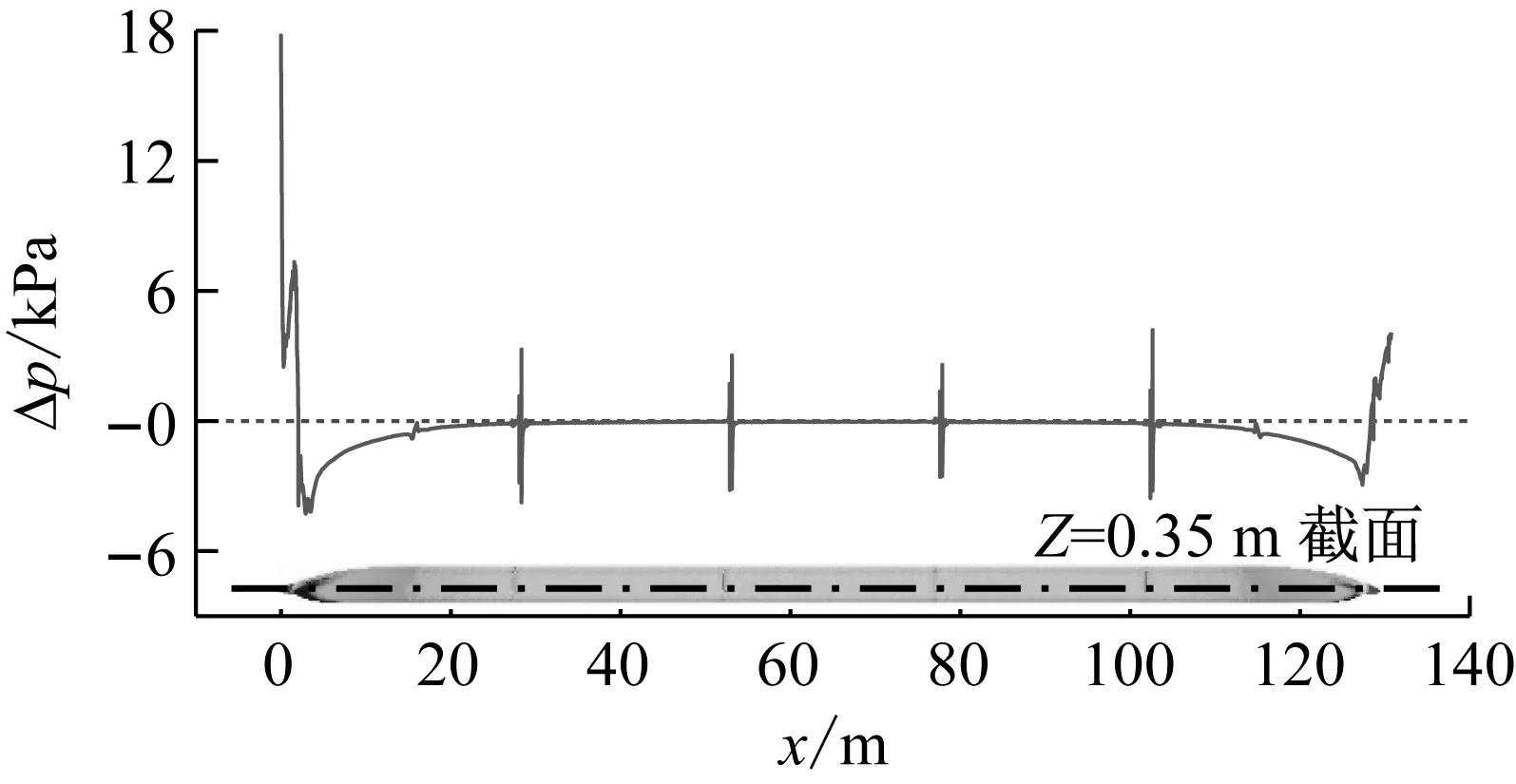
图10 车体水平截面的压力分布Fig.10 Pressure distribution of horizontal-sectional plane

图11表示了磁浮列车明线交会过程中，车体表面的压力变化情况。当车头通过观测列车时，鼻尖正压区先通过观测列车，观测点的压力上升，流线段的负压区随即通过观测列车，观测点的压力下降。因此，当车头通过时，观测列车瞬间受到正、负压力的相继作用。当车尾通过观测列车时，流线段的负压区先通过观测列车，观测点的压力下降；鼻尖正压区随后通过观测列车，观测点的压力上升。既车尾通过时，观测列车车体瞬间受到负、正压力的相继作用。平直车身通过时，观测列车的压力几乎没有变化。

(a) 车头通过

(b) 平直车身通过

(c) 车尾通过

2.3 明线交会压力波

2.3.1 各节车压力波

图12表示了两磁浮列车以600 km/h明线等速交会时，头车平直车身交会侧测点1和非交会侧测点2的压力时间历程曲线。由图12可知：相比交会侧压力，非交会侧的压力波动幅度很小，明线交会对非交会侧的压力影响较小，取交会侧的压力进行后续研究。

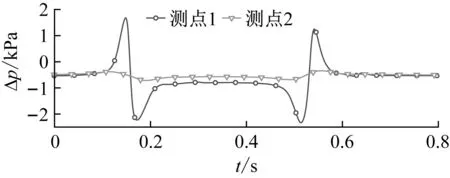
图12 头车平直车身测点压力Fig.12 Pressure of leading car’s straight body

图13表示了列车明线交会时，头车、3车和尾车平直车身交会侧测点1的压力时间历程曲线，将3车和尾车压力的时间进行平移，使不同车厢的压力峰值放到一起，便于对比。由图13可知：车头鼻尖正压区通过时，观测点压力快速增大到正峰值，车头曲线段负压区随后通过时，观测点压力快速减小，由正峰值快速变为负谷值，既“头波”；平直车身通过时，观测点压力处于微小的负压状态；车尾曲线段负压区通过时，观测点压力快速减小到负谷值，车尾鼻尖正压区随后通过时，压力由负谷值快速增大到正峰值，既“尾波”。因此，列车明线交会整个过程中，各节车厢交会侧压力都呈现出明显的“头波、尾波”，各测点受通过列车的压力作用时间也一样，各节车厢交会侧压力变化幅度相差不大。

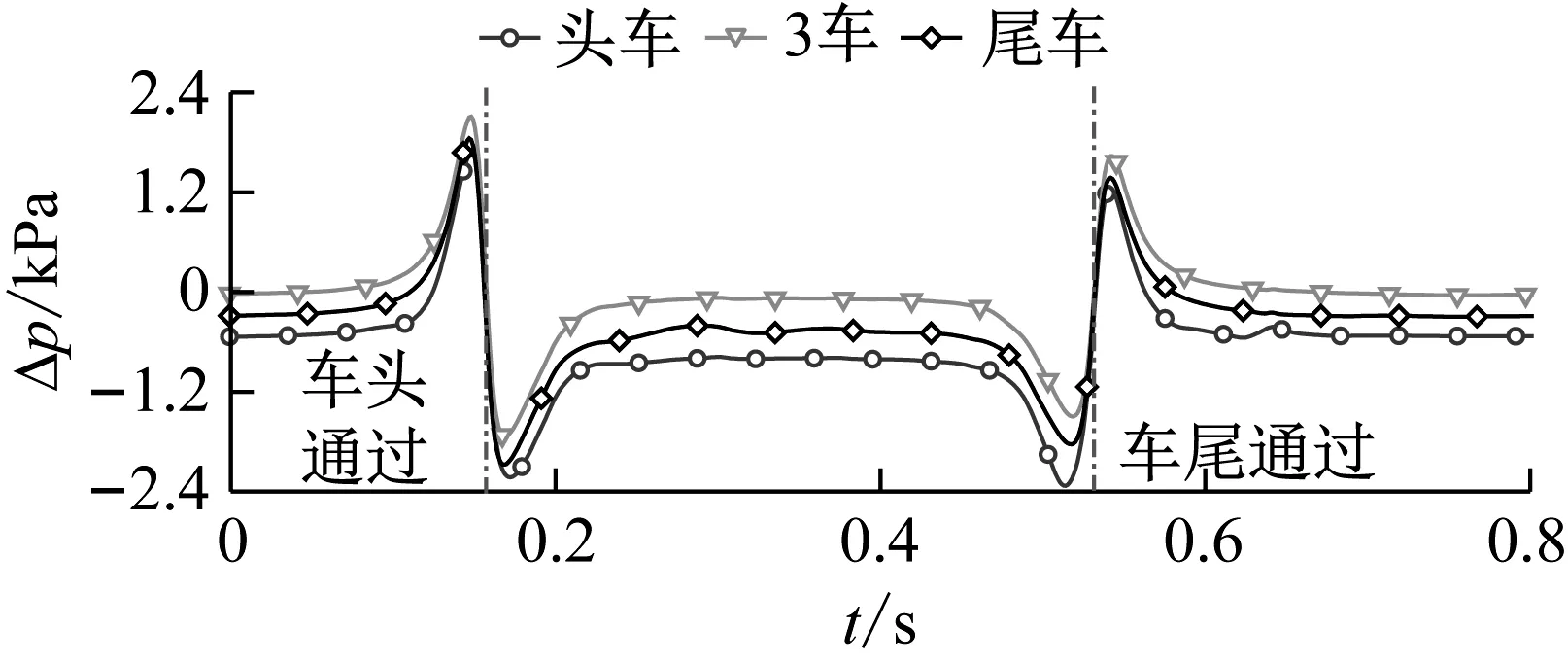
图13 不同车厢测点1压力Fig.13 Pressure of different cars’ point 1

表2统计了明线交会时各节车厢测点1的压力最值。由表2可知：头车的压力波动幅度最大，尾车的次之，3车的最小，所有中间车厢的压力波动幅度相差不大。头车的最大正压值为1.68 kPa，最大负压值为-2.33 kPa。表2中峰峰值是整个会车过程中，压力时间历程曲线中的最大值与最小值的差值，既会车压力波的峰峰值具体为Δp=pmax-pmin，pmax为会车压力波最大正压值；pmin为会车压力波最大负压值，见图9。气动力也是同样定义。

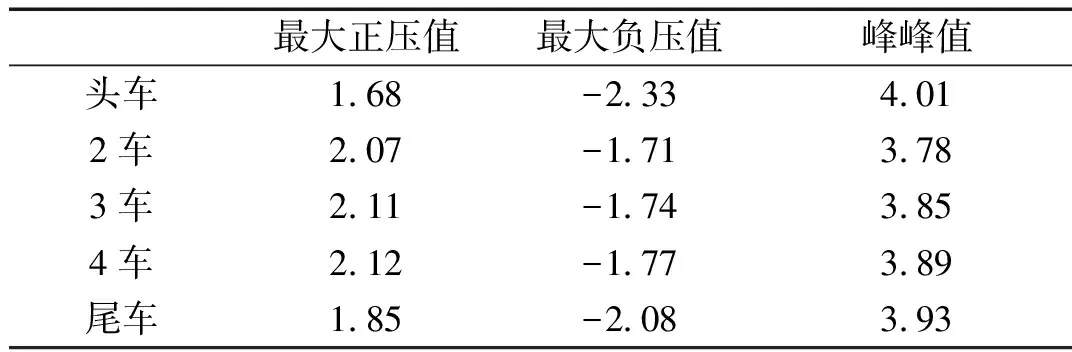
表2 各节车厢测点1的压力最值

2.3.2 车速对压力波的影响特性

以400、450、500、550、600和660 km/h明线等速交会时的压力波为例，研究车速对压力波的影响特性。由图13可知，不同车厢交会侧测点1的压力波动规律一样，因此，以头车的压力波为例，说明车速对交会压力波的影响。

图14表示了不同车速下，头车交会侧测点1的压力时间历程曲线。由图可知：不同车速下，同一测点的压力变化规律几乎一样，都呈现出明显的“头波、尾波”，列车速度对压力波动规律没有影响。列车明线交会速度越高，压力波的各个最值越大，压力变化越剧烈；车速对明线交会压力波最值和变化幅度有重大影响。明线稳定运行时，处于微小的负压状态，车速越高，负压也越大。

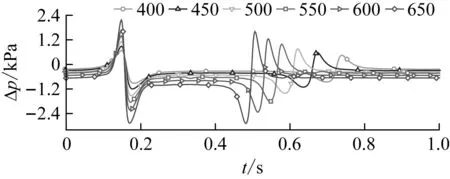
图14 不同车速下头车测点1压力(km/h)Fig.14 Pressure of leading car’s point 1 under different speeds(km/h)

为了定量说明车速对明线交会压力波峰值的影响，图15表示了压力波的最大正负压值以及拟合关系。压力波最大正负压值与车速的二次方函数近似成正比关系，拟合曲线拟合效果较好。头车压力最大正负压值随车速的增长速度比其他车厢都快。

2.4 明线交会侧向力

2.4.1 各节车厢侧向力

图16表示了列车明线交会时，头车、3车和尾车的侧向力时间历程曲线(图中黑色点划竖线表示通过列车头尾车鼻尖到达观测车厢中间位置时刻，其他图也一样)。正的侧向力表示车厢受到向外推的作用力，负的侧向力表示车厢受到向内推(朝向通过列车)的作用力。图中，将3车、尾车侧向力的时间轴进行平移，将各节车厢的侧向力峰值放到一起，便于对比。由图可知：通过列车车头通过时，观测列车各车厢侧向力快速增大到正峰值，然后快速减小到负谷值。既车头通过时，观测车厢受到先向外后向内的瞬变侧向气动力。车尾通过时，观测车厢受到先向内后向外的瞬变侧向气动力，侧向力的变化规律与车头通过正好相反。车头通过时侧向力的变化幅度大于车尾通过的。明线交会时，不同车厢受到的侧向力略有区别，头车在通过列车车头通过时，向外推力达到最大，尾车在车尾通过时，向外推力达到最大；对于向内推力，头车在车尾通过时最大，尾车在车头通过时最大，头尾车正好相反。对于中间平直车厢，向外、向内推力都在车头通过时，达到最大。

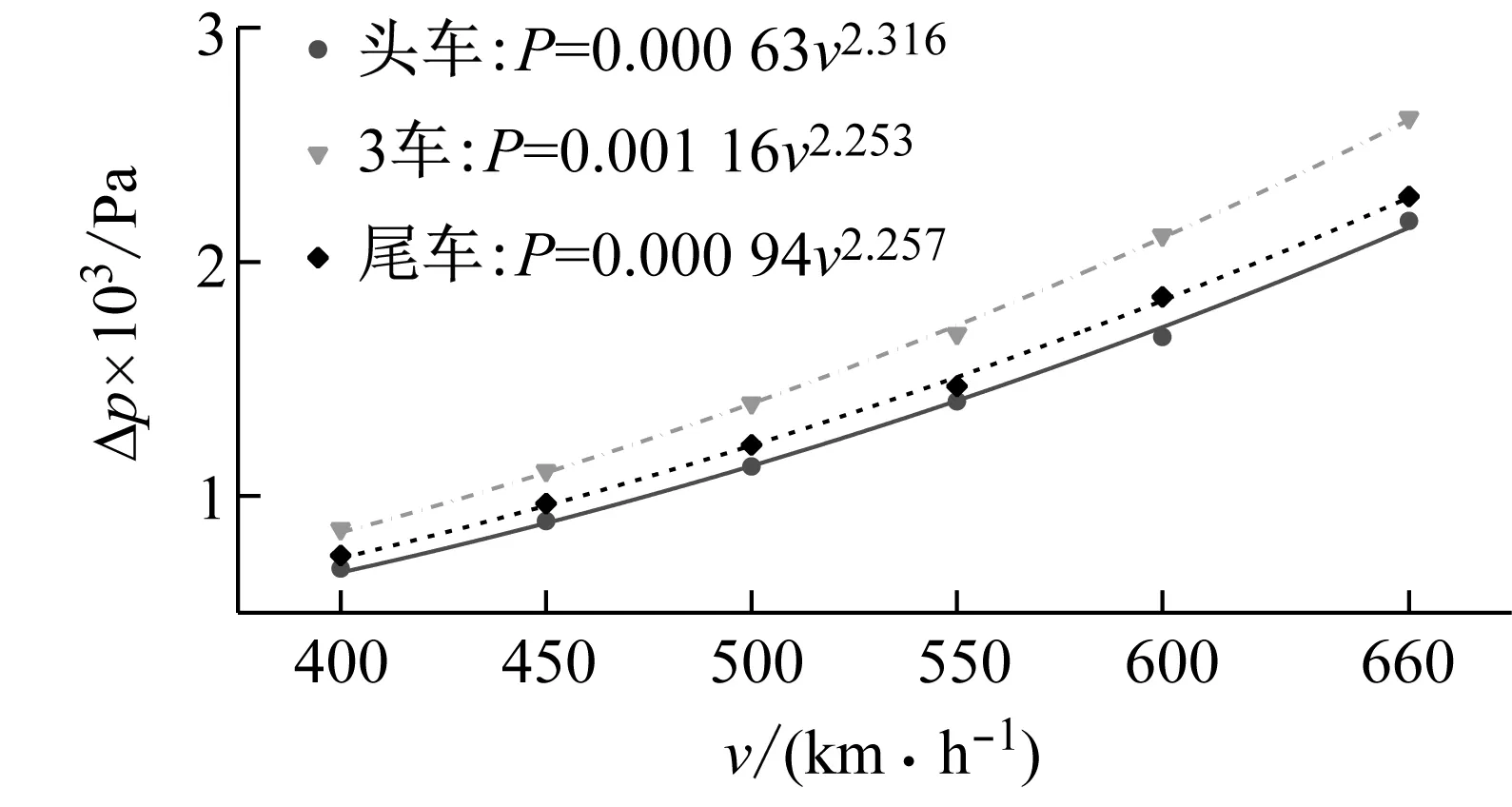
(a) 最大正值

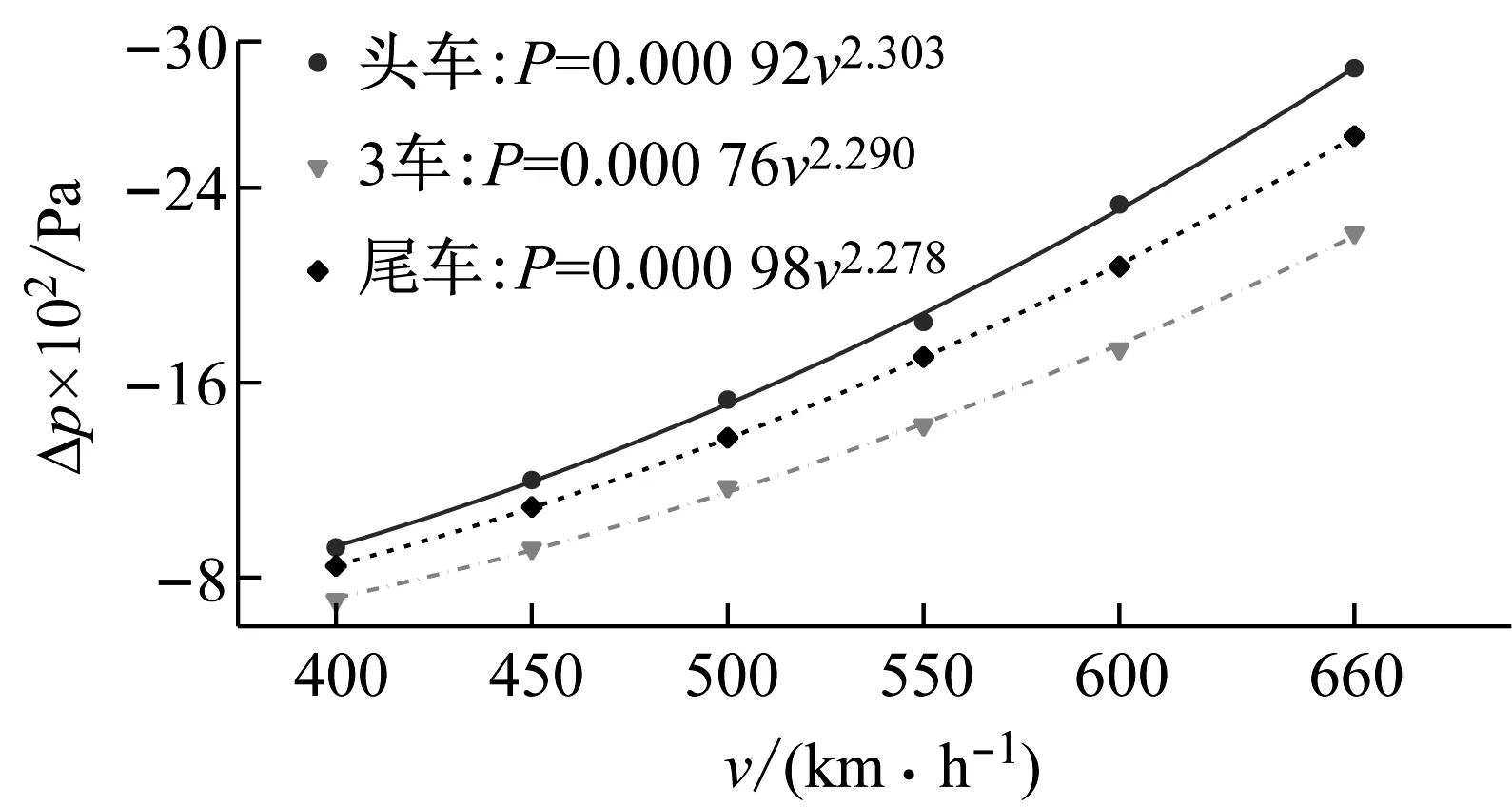
(b) 最大负值图15 车速对压力峰值的影响特性Fig.15 Train speed effects on pressure peaks

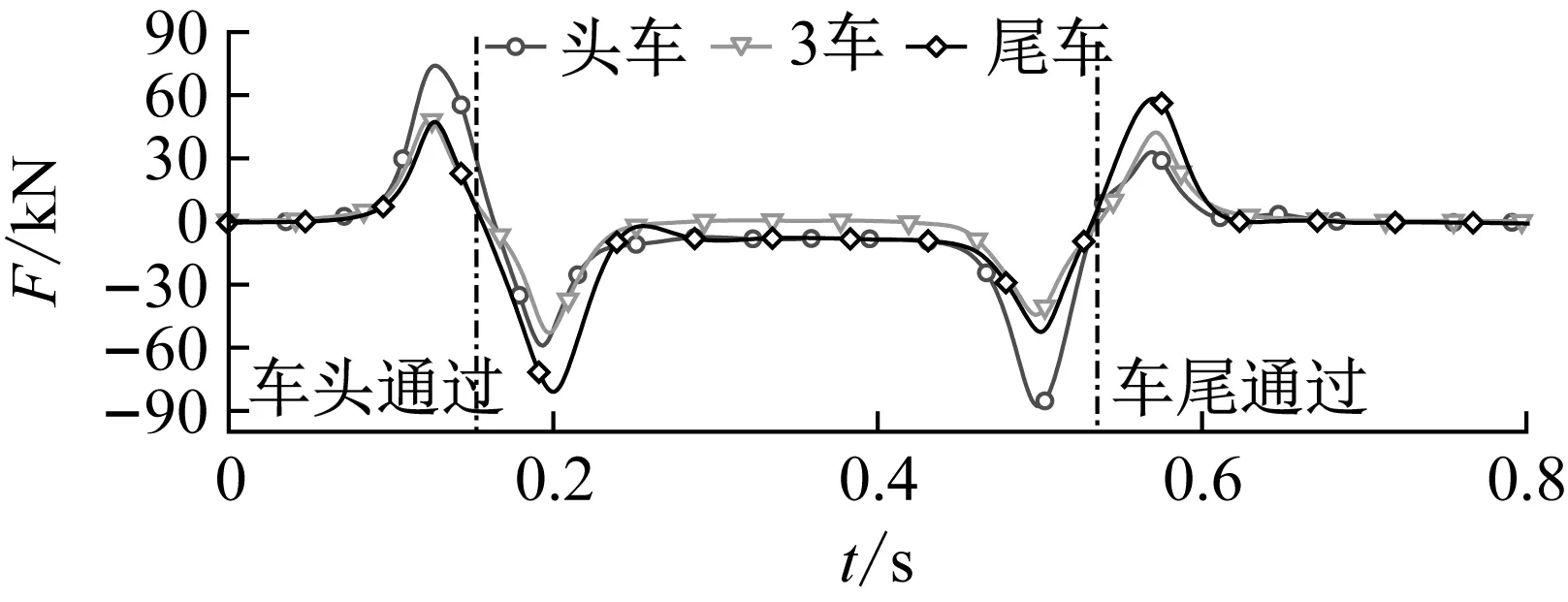
图16 不同车厢侧向力Fig.16 Lateral force of different cars

列车明线交会整个过程中，各节车厢都受到向内、向外推的两次侧向力交替作用，侧向气动力发生瞬时换向，对列车横向阻尼和电磁导向系统形成瞬态冲击，诱发车体发生横向振动，引起磁浮列车导向间隙变化，最终影响运行稳定性。

表3统计了明线交会时各节车厢侧向力的最值。由表可知：头车向外、向内推的侧向力都最大，尾车的次之，中间车的最小，所有中间车厢的侧向力最值相差不大。既头车的侧向力最为恶劣，头车向外推的侧向力最大值为73.99 kN，向内推的最大值为87.88 kN，尾车向内推的最大值为80.98 kN。

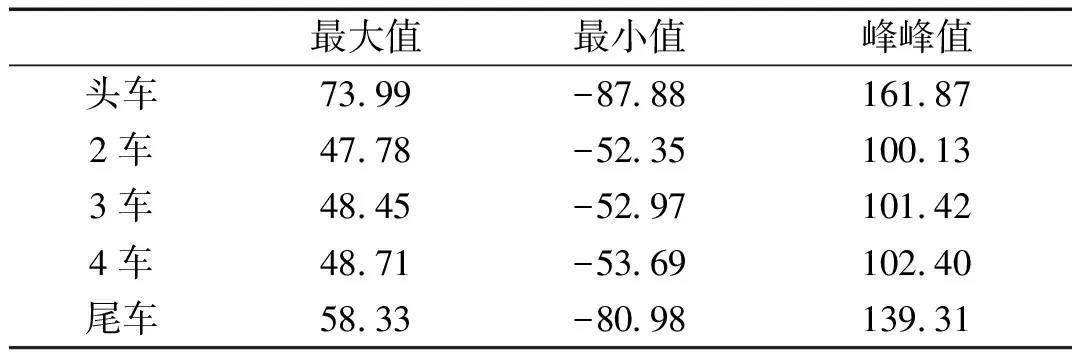
表3 各节车厢侧向力最值

2.4.2 车速对侧向力的影响

以400、450、500、550、600和660 km/h明线等速交会时的侧向力为例，研究列车速度对侧向力的影响特性。由图16可知，不同车厢的侧向力变化规律一样，因此以头车侧向力为例，说明车速对侧向力的影响特性。图17表示了不同车速下，头车侧向力时间历程曲线。由图可知：列车明线交会时，不同车速下的侧向力变化规律一样，都出现正、负侧向力的两次交替作用；不同的是，速度越高，侧向力的最值越大，侧向力变化越剧烈，车速对侧向力最值和变化幅度有重大影响。

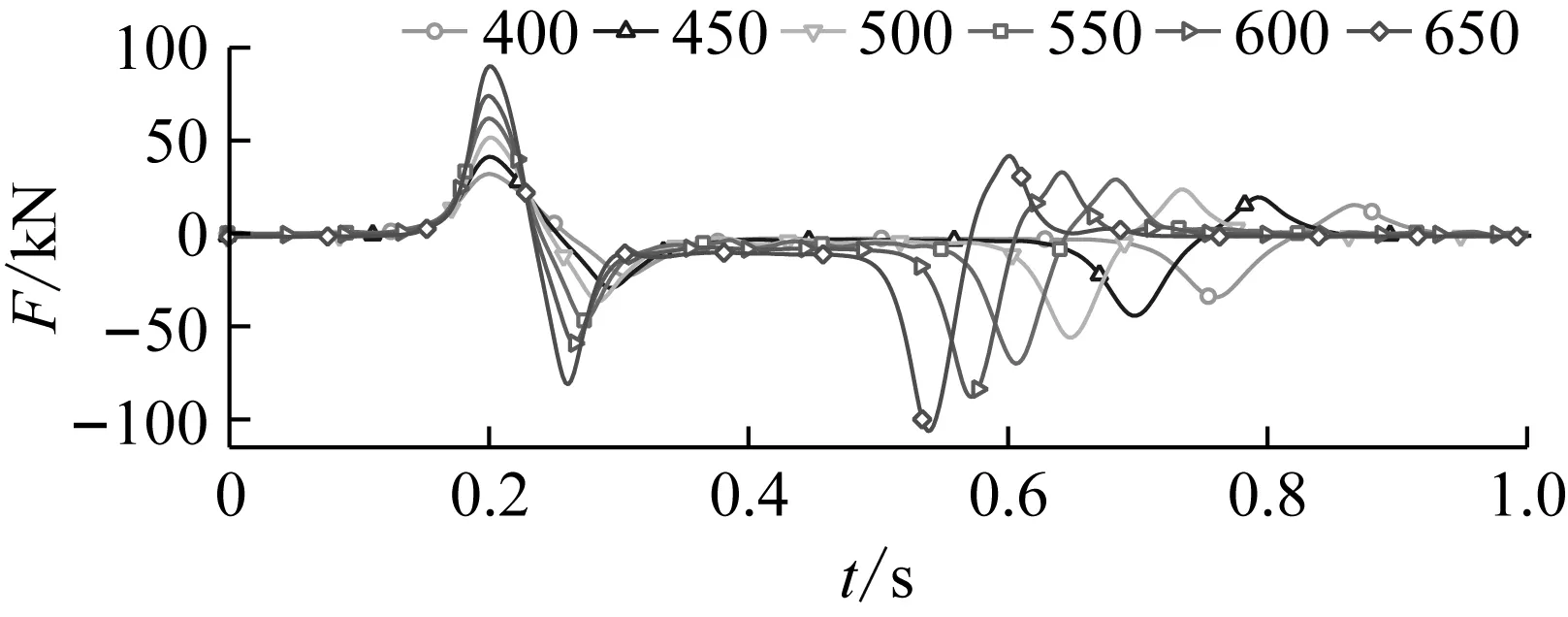
图17 不同车速下头车侧向力(km/h)Fig.17 Lateral force of leading car under different speeds(km/h)

为了定量说明车速对明线交会侧向力最值的影响，图18表示了各车厢侧向力的最大正负值以及拟合关系。侧向力最大正负值与车速的二次方函数近似成正比，拟合曲线拟合效果较好。头车侧向力最大正负值随车速的增长速度比其他车厢都快。

2.5 明线交会时的偏航力矩

图19表示了列车明线交会时，头车、3车和尾车偏航力矩的时间历程曲线。正的偏航力矩使车厢前部向外摆，负的偏航力矩使车厢前部向内摆(朝向通过列车)。图中将3车、尾车偏航力矩的时间轴进行平移，使各节车厢的偏航力矩峰值放到一起，便于对比。由图可知：通过列车车头经过时，观测列车各车厢的偏航力矩先快速增大到正峰值，然后快速减小到负谷值，最后又快速增大到正峰值。既车头通过时，观测列车各车厢先向外摆，再向内摆，之后又向外摆；尾车通过时，正好相反。车头通过时，偏航力矩的变化幅度比车尾通过时大。

明线交会时，头车或尾车经过时，在极短的时间内，观测列车各车厢都经历了偏航力矩两次瞬时换向，整个交会过程中，每节车厢都经历了偏航力矩的四次换向，偏航力矩的这种变化可能造成列车运行中短时的横向极不稳定，并对列车的侧摆阻尼造成较大的瞬态冲击，对电磁导向系统会有更高的要求。由于车头和车尾两端没有纵向车钩力的约束，偏航力矩的影响更加严重，严重时会引起头尾车横向稳定性失稳和“蛇行运动”。对于中间车，由于车厢两端受到纵向车钩力的约束，偏航力矩的影响相对较小。

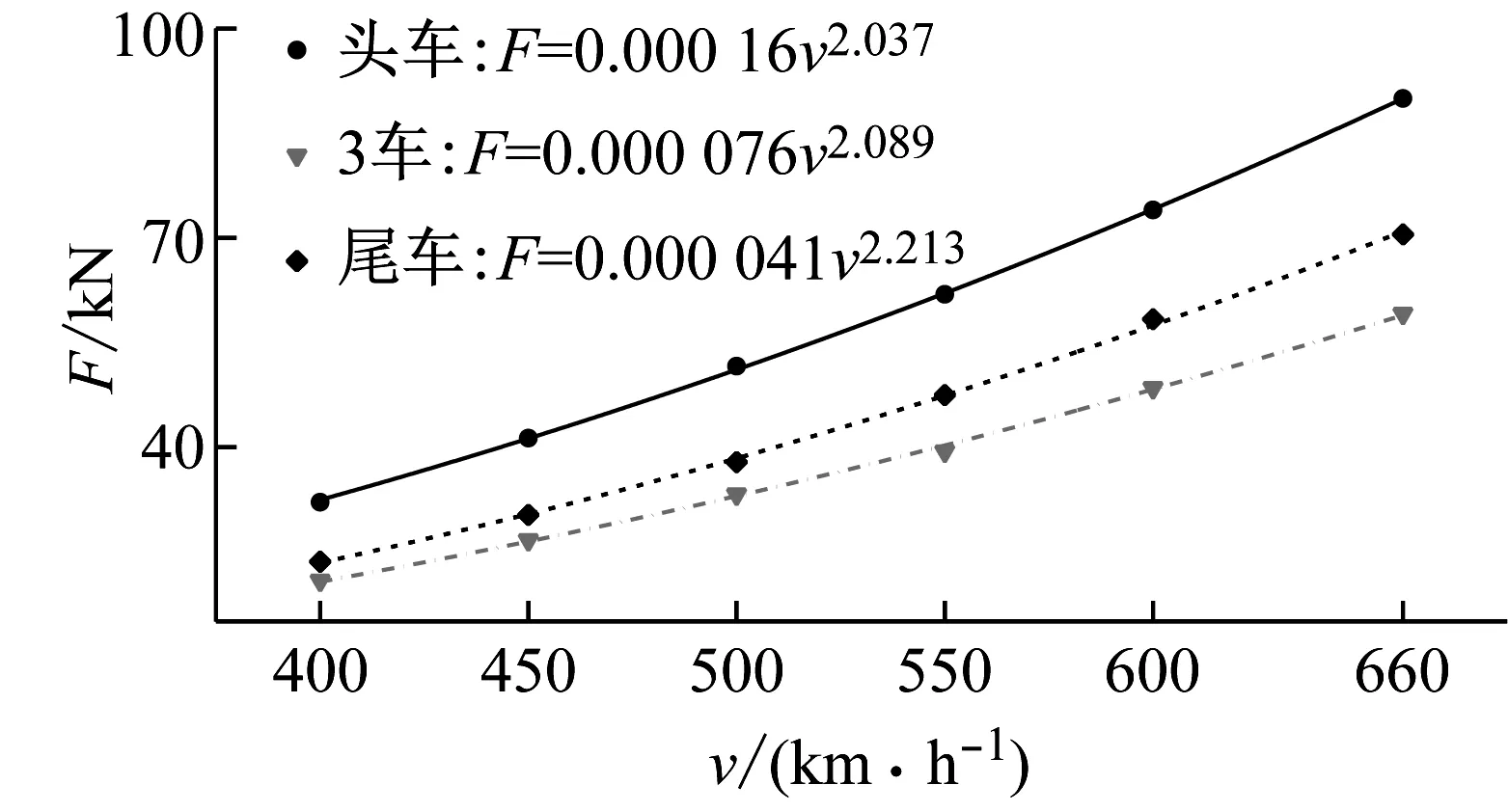
(a) 最大正值

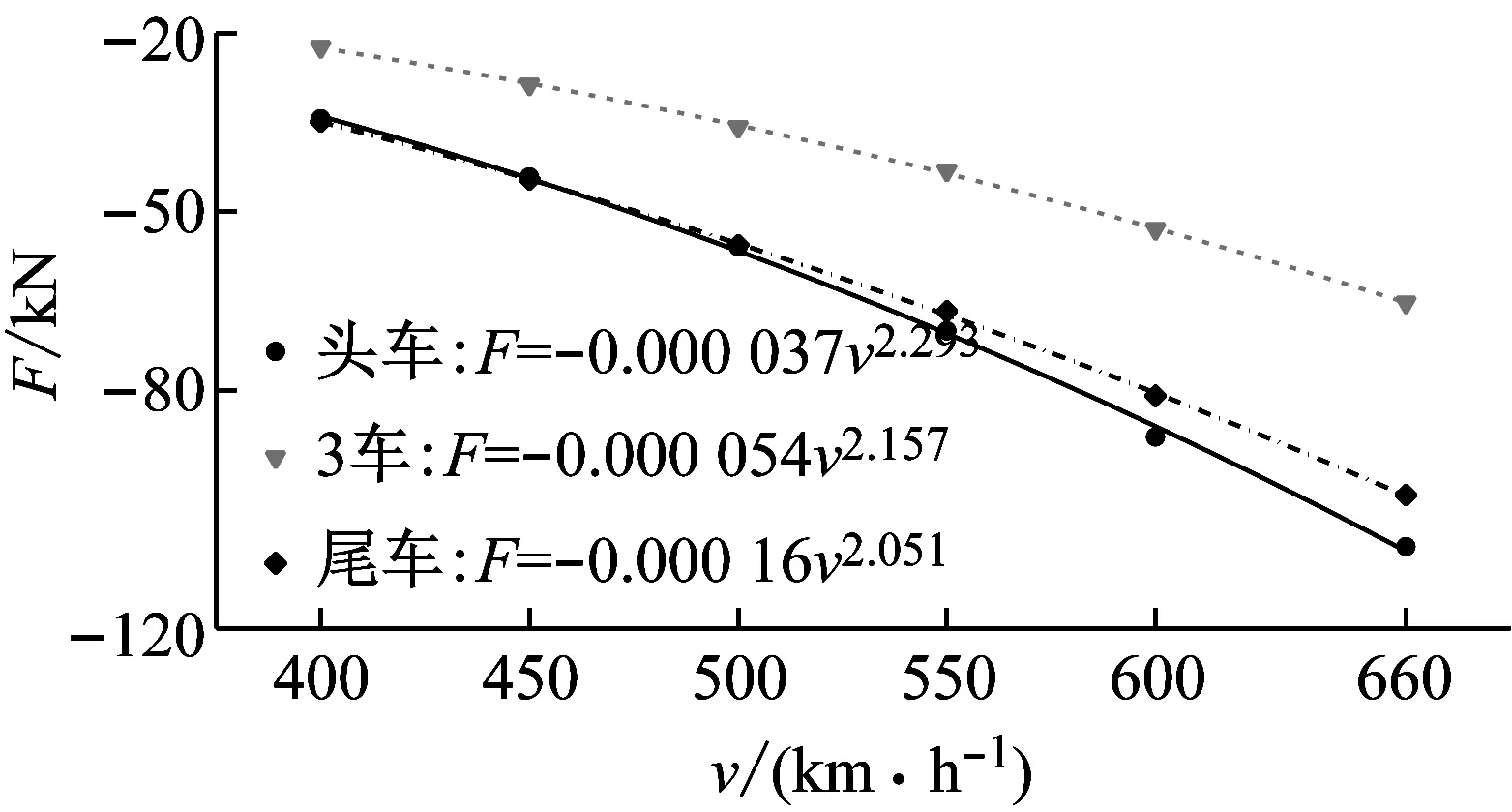
(b) 最大负值图18 车速对侧向力最值的影响特性Fig.18 Train speed effects on lateral force peaks

图19 不同车厢偏航力矩Fig.19 Yaw moment of different cars

表4统计了明线交会时各节车厢偏航力矩的最值。由表可知：头车向外摆的最大力矩明显大于其他车厢的，向内摆的最大力矩明显小于其他车厢的。所有中间平直车厢的力矩相差不大。头车向外摆的最大力矩为469.06 kN·m，尾车向内摆的最大力矩为458.38 kN·m。

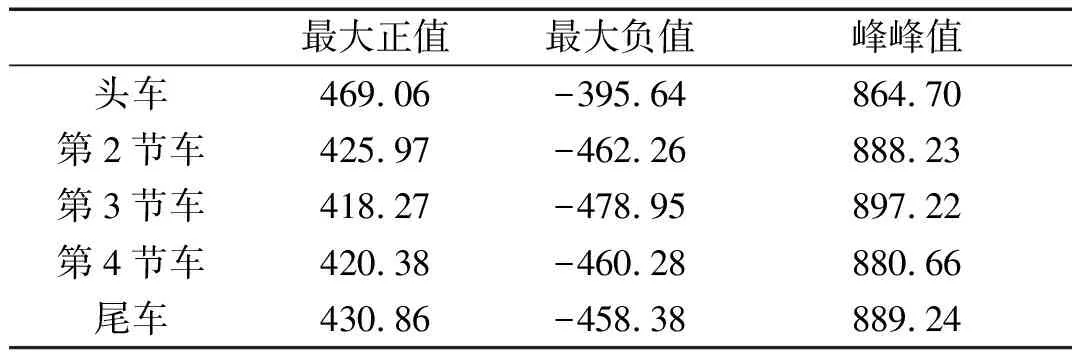
表4 各节车厢偏航力矩最值

2.6 明线交会时的侧滚力矩

图20表示了列车明线交会时，头车、3车和尾车侧滚力矩的时间历程曲线。正的侧滚力矩表示车厢有向外翻到的趋势，负的侧滚力矩表示车厢有向内翻到(朝向通过列车)的趋势。图中将3车、尾车侧滚力矩的时间轴进行平移，使各节车厢的侧滚力矩峰值放到一起，便于对比。由图20可知：通过列车车头通过时，观测列车各车厢侧滚力矩快速增大到正峰值，然后快速减小到负谷值。既车头通过时，观测车厢受到先向外后向内的瞬变侧滚力矩。车尾通过时，观测车厢受到先向内后向外的瞬变侧滚力矩，侧滚力矩的变化规律与车头通过时正好相反。车头通过时侧滚力矩的变化幅度大于车尾通过的。明线交会时，不同车厢受到的侧滚力矩略有区别，通过列车车头通过时，头车向外翻的侧滚力矩达到最大，车尾通过时，尾车向外翻的侧滚力矩达到最大；对于向内翻的侧滚力矩，头车在车尾通过时达到最大，尾车在车头通过时达到最大，头尾车正好相反。对于中间平直车厢，向外、向内翻的侧滚矩都在车头通过时，达到最大。

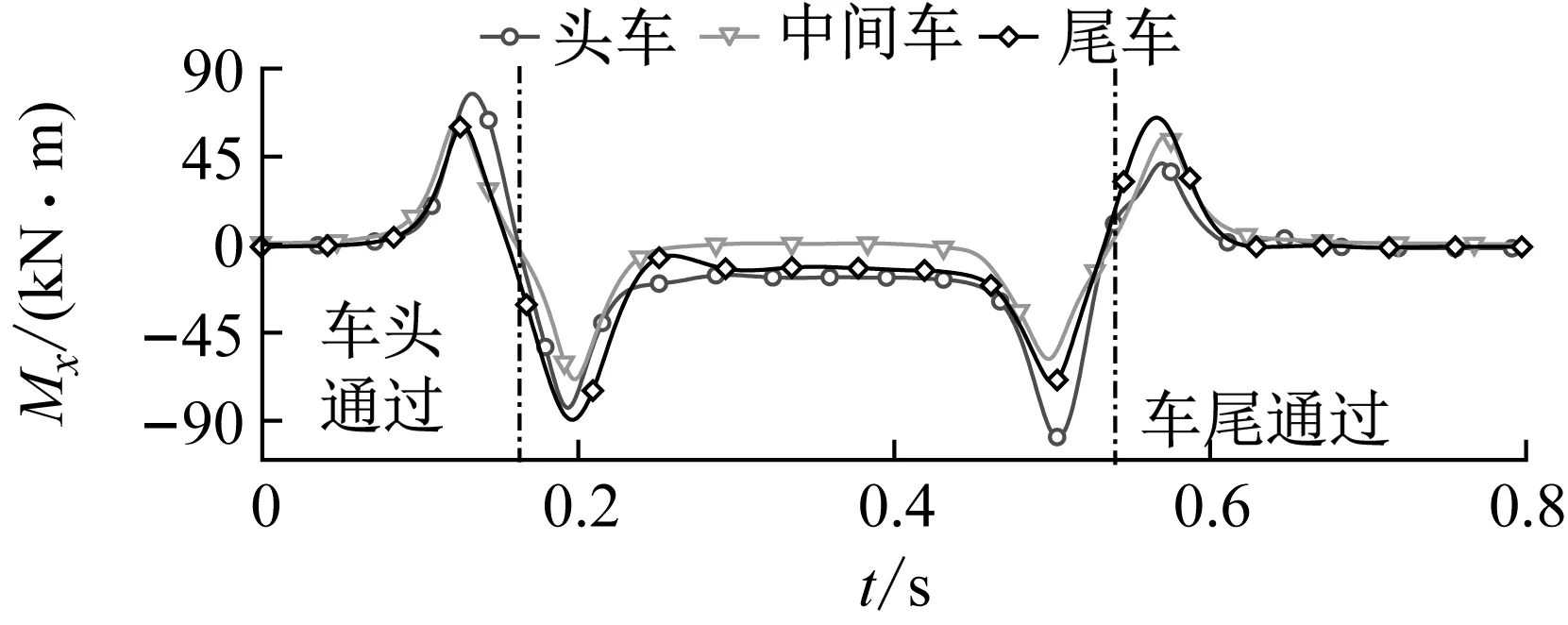
图20 不同车厢侧滚力矩Fig.20 Roll moment of different cars

明线交会时，在极短的时间内，各节车厢都受到正、负侧滚力矩的两次交替作用。侧滚力矩的剧烈瞬变对列车侧滚阻尼或防侧滚稳定器形成较大的瞬态冲击，对悬挂系统和电磁悬浮系统等提出更高的要求。侧滚力矩的瞬变导致车体发生侧滚运动，进而会引起磁浮列车悬浮间隙发生变化，最终影响磁浮列车的运行稳定性和安全性。

表5统计了明线交会时各节车厢侧滚力矩的最值。由表可知：头车向外翻和向内翻的侧滚力矩都最大，尾车的次之，中间车的最小，所有中间车厢的侧滚力矩最值相差不大。头车向外翻的侧滚力矩最大值为77.21 kN·m，向内翻的最大值为98.34 kN·m；尾车向内翻的最大值为89.51 kN·m。

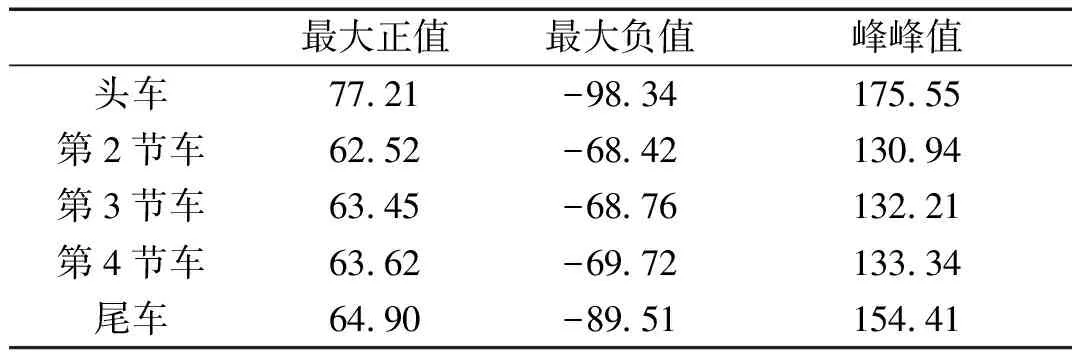
表5 各节车厢侧滚力矩最值

2.7 交会侧压力与气动力的作用关系

图21表示了磁浮列车明线交会时，不同车厢交会侧测点1的压力、侧向力、侧滚和偏航力矩的时间历程曲线。由图21可知：磁浮列车明线交会整个过程中，当车头通过时，观测列车各车厢的观测点压力、侧向力和侧滚力矩都呈现先正后负的波动趋势；偏航力矩先正后负，再正的波动趋势。车尾通过时的变化规律与车头通过时的正好相反。这主要是因为列车明线交会时，受通过列车车头鼻尖正压区、流线段负压区，以及车尾流线段负压区、鼻尖正压区的相继作用，使交会侧压力发生“稳定状态—增大—减小—稳定状态—减小—增大—稳定状态”的变化，导致各节车气动力产生相应的变化。明线交会整个过程中，交会侧压力与各节车侧向力、侧滚力矩和偏航力矩存在对应关系，交会侧压力对三个气动力有重大影响，对其变化其主导作用。

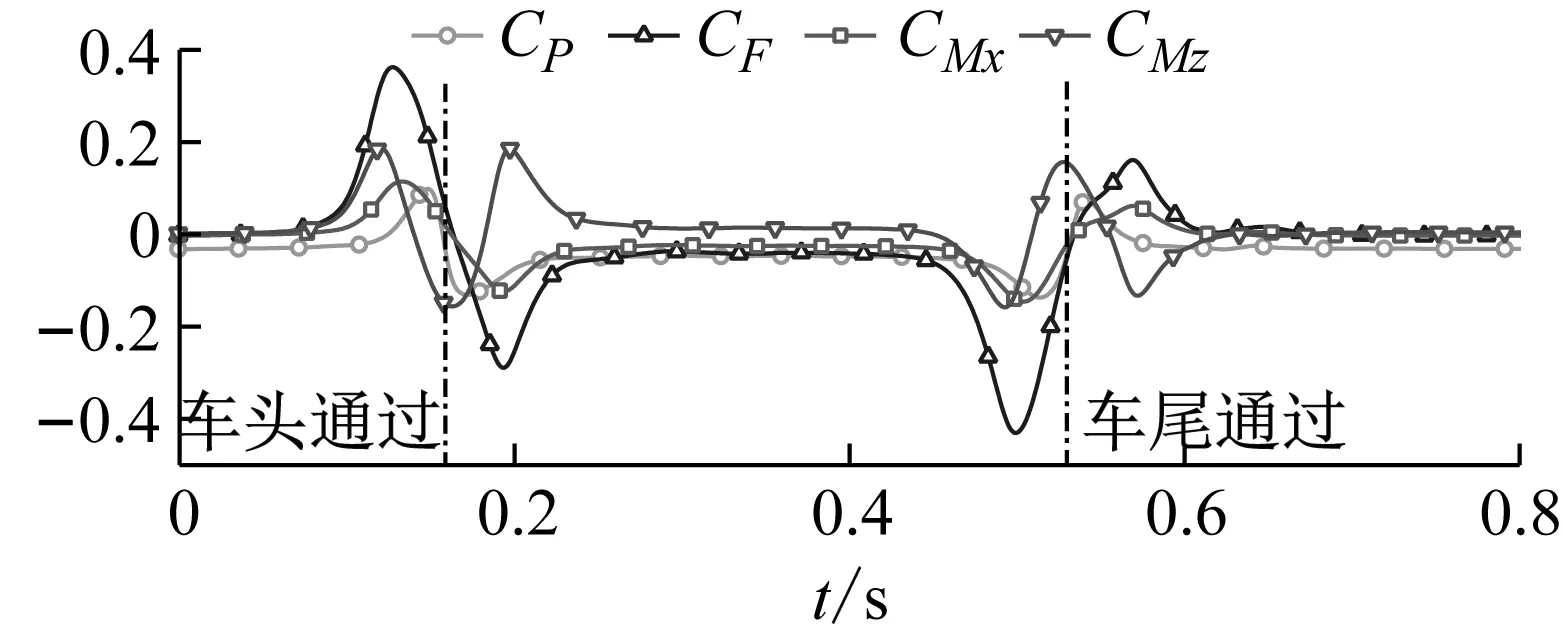
(a) 头车

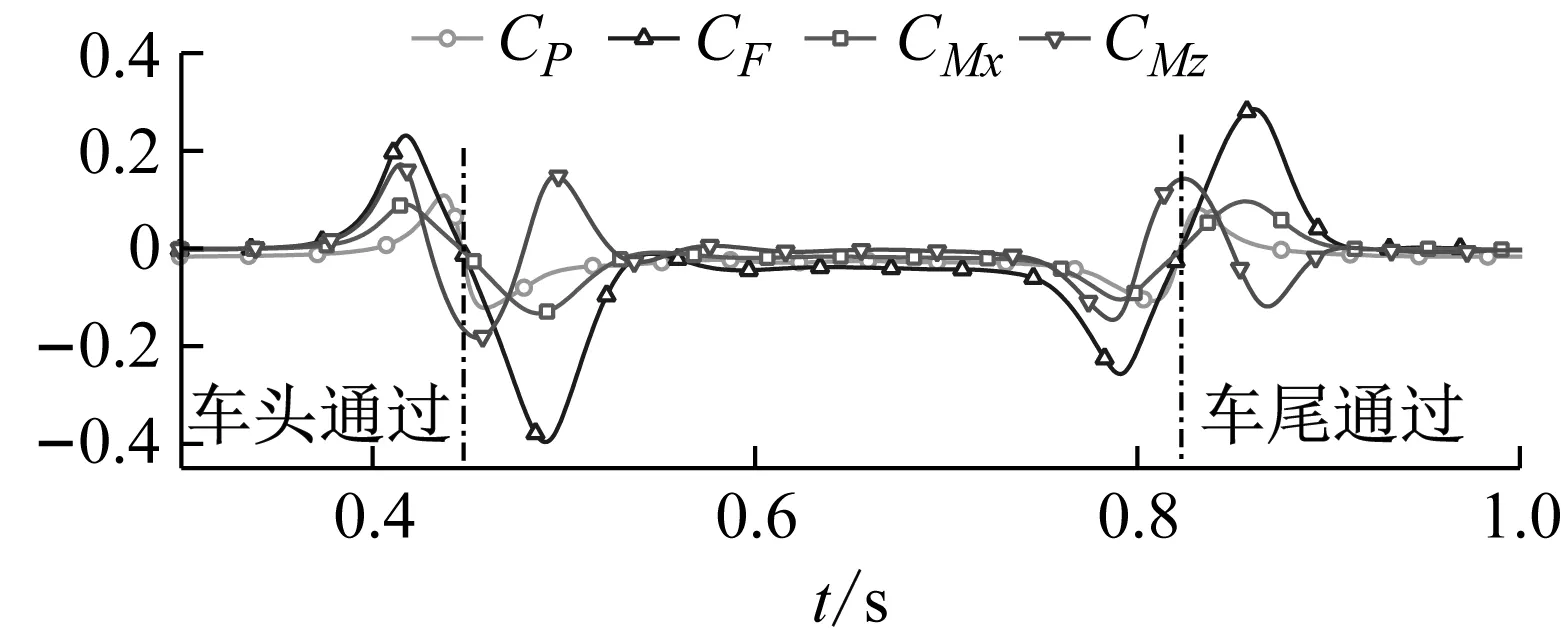
(c) 尾车图21 各节车交会侧压力、侧向力、侧滚力矩和偏航力矩Fig.21 The pressure, lateral force, rolling moment and yaw moment of different cars’

由于交会侧压力对列车横向气动性能起主导作用，而观测列车交会侧压力波动主要是由通过列车表面压力所引起的。600 km/h高速磁浮列车头尾车鼻尖与设备舱过渡区域的正压较强，设备舱导流区域与车体侧墙拐角区域的负压较强，如图22所示。导致明线交会时，受该区域压力的作用，交会侧压力发生剧烈波动，最终引起各个气动力发生剧烈变化。为了减缓明线交会时车体的横向摆动和侧滚运动，应降低该区域的压力波动，从空气动力学角度出发，可考虑将鼻尖与设备舱过渡区域、设备舱前端导流区域与列车侧墙拐角区域进行平顺化设计。

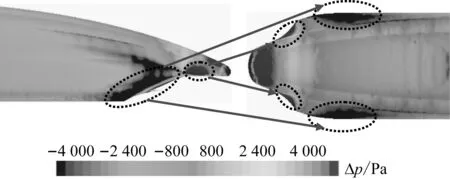
图22 流线段压力分布Fig.22 Pressure contour of stream line zone

根据侧滚力矩计算公式[26]，侧滚力矩主要由侧向力和升力引起，车底压力分布特性对列车气动升力有重大影响。图23给出了列车明线交会过程中，车头通过平直车身时，车体底部的压力分布特性。从图中可以看出，明线交会时，交会侧压力受通过列车表面压力的影响很大。头尾车流线段的正负压区通过时，引起观测列车车体底部交会侧的压力产生相应的正负压力波动；由于T型轨道梁对空气横向流动的限制作用，非交会侧车体底部的压力几乎没有波动。车体底部两侧的这种压力分布不均匀性导致使轨道两侧的车底气动升力相差较大，在气动侧向力的联合作用下，磁浮列车极容易发生倾覆事故。而且轨道两侧升力的不平衡性，对悬浮电磁力设置造成一定困难。

图23 列车底部压力Fig.23 Pressure contour of train bottom

3 结 论

采用三维数值模拟方法，对我国600 km/h高速磁浮列车明线交会横向气动性能进行研究，得出主要结论如下：

(1) 明线交会时，车体横向摆动和侧滚运动主要是由通过列车表面压力分布特性所引起的，特别是头尾车流线段的正负压。T型轨道梁对底部空气横向流动的限制作用，导致观测列车车体底部两侧压力分布不均匀，最终加剧了列车的侧翻运动。

(2) 明线交会时，车头通过观测列车时，侧向力和侧滚力矩都呈现出先正后负的波动趋势，偏航力矩呈现出先正后负，再正的波动趋势；车尾通过时变化规律正好相反。交会侧压力对侧向力、侧滚力矩和偏航力矩的变化其主导作用。

(3) 明线交会时，头车气动力的变化幅度比其他车厢都大，气动性能最为恶劣。以600 km/h等速交会时，头车侧向力向外推的最大值为73.99 kN，向内推的最大值为87.88 kN，向外摆的最大偏航力矩为469.06 kN·m，向内翻的最大侧滚力矩为98.34 kN·m。明线交会压力波和侧向力最值与车速的平方近似成正比关系。

(4) 为减缓明线交会时列车的横向摆动和侧滚运动，可考虑将鼻尖与设备舱过渡区域、设备舱导流区域与车体侧墙的拐角区域进行平顺化设计。